几道题的解法之我见
☉江苏省南京金陵中学河西分校 李玉荣
几道题的解法之我见
☉江苏省南京金陵中学河西分校李玉荣
解题研究是数学教师日常教学的一门必修课.陌生题的出现、新编题的诞生,促使教师长年累月地进行解题研究.解题策略的不同,决定了解题“长度”的不同.降低解题难度、增大解题智慧,是教师解题研究应该追求的理想目标.拜读贵刊2016年第1期刊载的文1、文2,对文中的几道例题的解法有所思考,撰文与读者分享.
【评注】这是1992年高考数学理科题,文1是利用换元法转化为一元二次方程求解的,解法不够简洁.
题2:(文1中的例5)设a>0,b>0,且满足,则的值是().
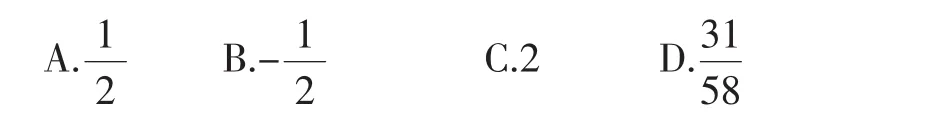
(舍去负值),所以a=25b.
【评注】文1中的解法将已知等式变形所得的方程较为复杂,后利用换元法得到分式方程,求解不够简洁.
题3:(文1中的例2)若(z-x)2-4(x-y)(y-z)=0,求证:x、y、z成等差数列.
解:以(x-y)、(y-z)为根的一元二次方程为[t-(xy)][t-(y-z)]=0,即t2+(z-x)t+(x-y)(y-z)=0.
因为Δ=(z-x)2-4(x-y)(y-z)=0,所以方程两根相等.
从而x-y=y-z,即x、y、z成等差数列.
【评注】这是1979年高考数学理科题,文1中的解法也是用方程的观点处理的,但牵涉到分类讨论,思维较复杂,还运用了根的判别式、观察出方程的根t=1、韦达定理等知识,解法不够简洁.
题4:(文1中的例3)已知a+b+c=0,a2+b2+c2=4,求a4+ b4+c4的值.
解:由于a+b=-c,a2+b2=4-c2,则ab=[(a+b)2-(a2+ b2]=c2-2.
所以a4+b4=(a2+b2)2-2a2b2=(4-c)2-2(c2-2)2=-c4+8.
从而a4+b4+c4=8.
【评注】文1中的解法莫名其妙地提到一元二次方程,但计算过程中又没用到,而且计算的ab=c2-4是错误的.值得一提的是,此题可拓展为:已知a+b+c=0,a2+b2+ c2=k(k为常数),求a4+b4+c4的值.用笔者的解法不难求得结果为
题5:(文2中的题2)如图1,在△ABC中,AB=AC,∠A=20°,点D、E分别在AB、AC上,∠ACD=20°,∠ABE= 10°,求∠DEB的度数.
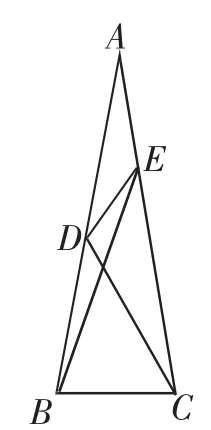
图1
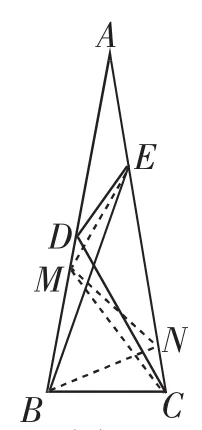
图2
解:如图2,在AB上取点M,使ME=AE,则∠AME= ∠A=20°.
由∠ABE=10°,得∠MEB=∠AME-∠ABE=10°.
则BM=ME.
在AC上取点N,使MN=MB=ME.
则∠MNE=∠MEN=∠A+∠AME=40°.
则∠EMN=180°-2×40°=100°.
从而∠BMN=180°-∠EMN-∠AME=60°.
故△BMN为等边三角形,所以BN=BM,∠MNB=60°.
则∠BNC=180°-∠MNB-∠MNE=80°=∠BCN.
由∠MDC=∠A+∠ACD=40°=∠MEC,得E、D、M、C四点共圆,则∠DEC=∠BMC=50°.
由∠BEC=∠A+∠ABE=30°,得∠DEB=∠DEC-∠BEC=50°-30°=20°.
【评注】此题在文2中是由“兰利问题”变式而成的,其提供的解法借助兰利问题的图形及辅助线,通过两次三角形相似求解,解答的“长度”非同一般,而笔者不是先构造“兰利问题”的图形,而是先作ME=AE,再逐步得到“兰利问题”,求解过程较为简洁.
解题研究永无止境,只要肯做有心人,方法会在勤思中应运而生.不论是教师还是学生,都能够在研究解题中不断地积累数学的素养,以及加深对数学的理解.
参考文献:
1.黄树军,谢东银.例谈巧构一元二次方程解题策略[J].中学数学(下),2016(1).
2.李艳娜.“兰利问题”求解的多种途径[J].中学数学(下),2016(1).

