践行“用教材教”，追求“智慧课堂”——以“平方根（第1课时）”教学为例

☉江苏省南通市启秀中学　龚　震



践行“用教材教”，追求“智慧课堂”——以“平方根（第1课时）”教学为例

☉江苏省南通市启秀中学龚震

专家教师李庾南老师一直倡导“单元教学”，特别是在单元教学的起始课，基于数学内部发展的逻辑连贯式的数学情境创设，也是李老师几十年来一直亲力亲为的教学追求.作为李老师的弟子，近期有机会在一次赛课活动中执教“平方根（第1课时）”，就是践行李老师的“单元教学”，引导学生逆向思考，生成新知，概括性质，对话生成，取得较好的教学效果，本文整理该课的教学实录，供研讨.

一、教学过程

（一）目标解析

（1）通过对逆向思维的引导，以及与旧知识的对比生成新概念，对学生现有的知识体系扩充、延伸，进一步完善.

（2）在加深对新生成概念的理解中，通过大量的实例总结、概括出性质.

（3）在数学活动中，逐步学会自主、合作、探究的学习形式.

（二）教学重点与难点

平方根的性质，对平方根意义的理解.（三）教学方法与手段

“自学、议论、引导”教学法.（四）教学流程1.开课阶段

在复习旧知识的过程中引导学生逆向思考，感受平方与开平方两种互逆运算，比较两种运算的联系与区别，生成开平方运算与平方根的定义.先安排学生复习乘方运算及指数、底数、幂的概念，并启发学生思考“反过来呢？”，为了清楚地说明开课阶段的教师行为，附板书片断如下.

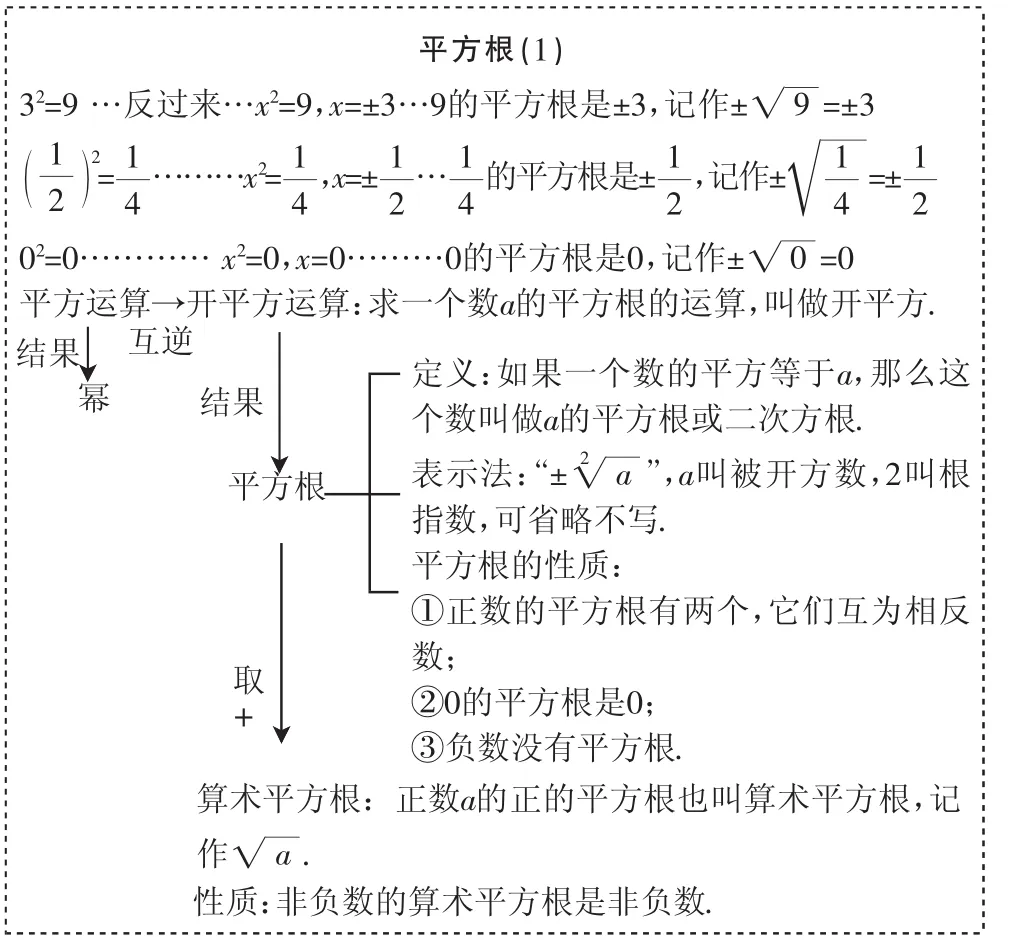
教学预设：平方运算中，已知底、指数求幂；这个运算中，已知指数、幂求底数，是不是平方运算？和平方运算是什么关系？是平方运算的逆运算，取个名称——开平方运算，开平方运算的结果叫做平方根.接着板书定义.

平方根：如果一个数的平方等于a，那么这个数叫做a的平方根或二次方根.

开平方：求一个数a的平方根的运算，叫做开平方.

接着追问（指着黑板上面的板书）：9的平方根是_______，的平方根是_______，0的平方根是_______.

追问：上例中，被开方数是什么？运算的结果是什么？叫做什么？怎样表示？

设计意图：以复习平方运算为切入点，引导学生逆向思考；通过与平方运算的对比，让学生自主概括开平方运算的概念，体会出这是一种新的运算，使整个过程中凸显“自然”.

2.探究新知

活动1：（1）学生上黑板，教师出题，其余学生在下面写（只表示，不写结果）；

（2）第二批学生上黑板写出结果.

活动2：小组长出题，其余组员答，然后各小组交流.

预设互动：在自主探究、合作交流的基础上，揭示、概括平方根的性质；由平方根的性质自然生成算术平方根的定义.练、议，深化对平方根意义的理解，接着设计如下问题.

问题1：前面举的例子中为什么没有负数？（紧扣定义“一个数的平方等于a”）±

问题2：平方根有什么特点？学生自主探究出如下性质，教师板书.

性质：①正数的平方根有两个，它们互为相反数；

②0的平方根是0；

③负数没有平方根.

设计意图：由性质①自然生成算术平方根的定义，并跟学生讲清如下注意点，第一，算术平方根：正数a的正的平方根也叫做算术平方根，记作；算术平方根与平方根的关系：算术平方根是平方根中正的那一个，接着适当举例加深理解；最后还要强调性质：非负数的算术平方根是非负数.

问题3：还有什么运算的结果是非负数？

预设学生归纳：一共学了“3种”非负数：a2、|a|、（a≥0）.

巩固练习如下所示.

（1）求下列各数的平方根：

（2）求下列各式的值：

（3）判断下列说法是否正确.

①5是25的算术平方根；

③（-4）2的平方根是-4；

④0的平方根与算术平方根都是0.

设计意图：在得到了平方根及其相关概念后，通过设计两个练习，一是为强化、巩固平方根的定义；二是为以后学生探究、概括平方根的性质及算术平方根的相关知识作铺垫，由特殊到一般.

3.师生共同总结

师生共同回顾本节课所研究的内容及知识形成的过程，提出如下小结问题.

小结问题1：平方运算与开平方运算有什么关系？（是互逆运算）

小结问题2：开平方是运算名称，它的运算结果叫什么？（平方根）

小结问题3：我们已经学过哪些运算？（加、减、乘、除、乘方、开平方）开平方与其他运算的不同之处是什么？

小结问题4：平方根与算术平方根有怎样的关系？

4.附板书设计

二、教学立意的进一步解读

1.践行单元教学，整合教学内容，努力“用教材教”

本章原来教材中的处理方式是：先生成算数平方根的概念，后生成平方根的概念.笔者认为这种方式与学生正常的认知规律不太符合，所以对教材进行了适当整合.学生在过去已经学习了加、减、乘、除、乘方五种运算，其中加和减、乘和除都是互逆的运算.本节课开始由复习乘方运算切入引出其逆运算——开平方运算，然后在举例加深、强化概念的同时设下伏笔，紧接着由学生自主探究平方根的性质，在概括性质的时候再自然引出算术平方根的概念，并由学生揭示算术平方根的性质.这样，整个教学过程从头到尾，无论是教师的问题设置，还是学生整堂课的思维轨迹，都显得比较自然.

2.注重预设追问，促进课堂对话，追求“智慧课堂”

从上面的课例来看，我们注重预设了大量的追问，通过系列追问促进了课堂上的对话，而且这些对话也是李庾南老师在“自学·议论·引导”教学论中所指出的生生对话、师生对话等多种形式；此外通过预设学生上台出题目，其他学生上台板演、答辩等环节，激活课堂氛围，让生与生之间的思维碰撞，把学生的数学思维都卷入在课堂学习中，提升课堂教学效率，也追求了李老师倡导的“智慧课堂”.特别值得一提的是，整个过程中，教师的主导作用似乎淡化了许多，变成了学生为主体的学，然后在学生“学”为中心的表面之后，教师“站在了后面”“设计在课前”，要付出的努力会更多.

参考文献：

1.钟启泉.新旧教学的分水岭［J］.基础教育课程（上），2014（2）.

2.李庾南.自学·议论·引导教学论［M］.北京：人民教育出版社，2013.

3.章建跃.全面深化数学课改的几个关键［J］.课程·教材·教法，2015，35（5）.

4.刘东升.悠然神会，妙处与君说——李庾南老师平方根课例赏析［J］.中国数学教育，2014（5）.

5.马公仕.靠近“最近发展区”，聚焦初中几何特点——以七年级“直线、射线、线段”教学为例［J］.中学数学（下），2015（3）.