改编习题注重关联，系统开发引领思考——以“勾股定理”相关编题为例

☉浙江省宁波市北仑区顾国和中学　陈　波



改编习题注重关联，系统开发引领思考——以“勾股定理”相关编题为例

☉浙江省宁波市北仑区顾国和中学陈波

华东师大钟启泉教授指出：“‘练习’的系统开发是每一个教师义不容辞的责任”“练习是一个系统，应当把练习作为一个系统来开发”.基于上述认识，我们在新学期“勾股定理”教学期间，有计划地研制了一系列深度改编的习题，并在所在学校、班级积极实践，取得了一定的教学效果，本文展示相关题例，并跟进解读阐释设计意图，供研讨.

一、题例展示与解读说明

题1：如图1，在四边形ABCD中，AB=3，BC=4，CD=12，AD=13，∠B=90°.

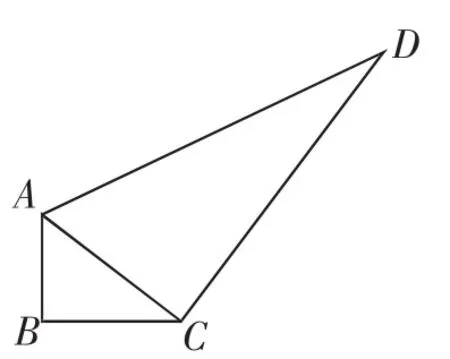
图1

（1）求AC；

（2）求证：△ACD是直角三角形；

（3）求四边形ABCD的面积.

编题说明与教学手记：这道习题改编自教材原题，原题只要求四边形ABCD的面积，根据教学经验，发现不少学困生往往找不到答题的思路，或者是直接“想当然”认为∠ACD是直角，从而造成“跳步解答”.基于上述教学现实，我们通过增设两个小问，为学生设计了更为平缓的铺垫，为一些学困生解决这类问题提供了方法上的引导.

题2：如图2，在正方形ABCD中，E是BC的中点，F是CD上一点，且CF=CD.

图2

（1）若正方形ABCD的边长为4，求AF、EF的长；

（2）猜想△AEF的形状，并说明理由；

（3）取AF的中点G，连接EG，设EG=m，记正方形ABCD的面积为S，试用含m的式子表示S.

编题说明与教学手记：这道习题源于教材，教材上一般都是直接设问“图中有几个直角三角形”，有些同学由于缺少深入的思考、演算，常常会缺少对△AEF的形状的认识.我们基于教学现实，重新增加了第一问，给正方形的边长赋一个特殊数值，然后安排学生先计算、体验一下相关线段的数据，这样可以对学生思考第二问有所启示.然而就练习反馈情况来看，又出现一些学生缺少对并列式设问与递进式设问的理解，造成将第一问的结论直接代入第二问演算说明的问题.到了第三问，将问题从常量引向变量，从特殊走向一般，也是渗透学生即将要接触的变量与函数思想.

题3：如图3，△ABC的三边a、b、c满足|a-3|+（b-4）2+（c-5）2=0.

（1）求证△ABC是直角三角形；

（2）求斜边上的高；

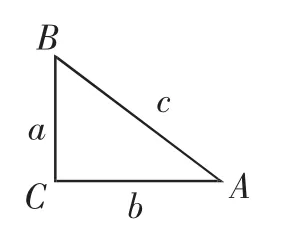
图3

（3）以△ABC的三边为边分别向外作正方形，它们的面积分别是S1、S2、S3，请直接写出它们之间的数量关系；

（4）以△ABC的三边为直径分别向外作3个半圆，通过计算分析这三个半圆的面积关系；

（5）以AB为边向△ABC外作△ABD，使△ABD为等腰直角三角形，画图分析并直接写出AD的长；

挑战：（以下两题，供选择一题解答）

（6）若边AB上有一点H，当点B关于直线CH的对称点B′落在线段AB上时，求AB′的长；

（7）如图4，分别以等腰Rt△ABC的边AB、AC、BC为直径画半圆，若BC=a，求两个月形图案AGCE和BHCF的面积之和（图中阴影部分）.（用含a的式子表示）

图4

编题说明与教学手记：前的问属于基础问题，第三、四、七问属于一个系列的问题；第二、六问可看成是一个变式拓展的过程.安排给学生的解答时间是25分钟，一个班55个学生，有5人能全部答对；答对4问的全班达到40人，基本达到预期目的.值得一说的是，第七问还可以“从特殊走向一般”，即将“等腰Rt△ABC”变式为“Rt△ABC”，这样的话两个月形图案AGCE和BHCF的面积之和仍然等于Rt△ABC的面积.

题4：如图5，将一个边长分别为4、8的长方形纸片ABCD折叠（折痕为EF），使C点与A点重合，设BE=x.

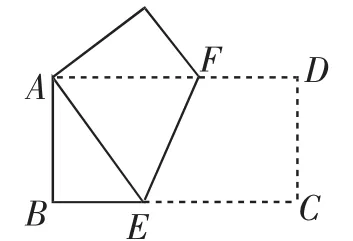
图5

（1）用含x的式子表示AE；

（2）求x；

（3）求DF的长；

（4）求EF的长；

（5）连接AC，求证：AC、EF互相垂直平分；挑战：

（6）将“题干”改成“边长分别为a、b（b>a）的长方形…”，其余不变，记△AEF的面积为S，试用含a、b的式子表示S.

编题说明与教学手记：以矩形为背景的折叠问题，常常需要利用勾股定理、借助方程工具来实现求解.这道习题是各级各类考试中的高频考题，为了在学生初学期间接触该类问题就形成深刻印象，我们把这类问题的思考通过增设第一、二、三问，充分展开思考过程，既是提供引例、铺垫，也是示范和引领学生学会解决这类问题.对于第五问，则是关联菱形的对角线性质，而第六问鼓励优秀学生挑战潜能，也是数学从特殊走向一般，从常量走向变量的数学研究取向.

题5：如图6，平面直角坐标系xOy中，已知点A（0，4）、B（b，-1），且S△AOB=6.

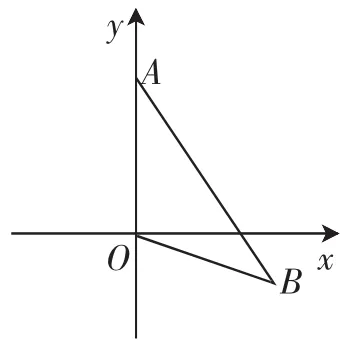
图6

（1）求b的值.

（2）求线段AB的长.

（3）若点M（m，0），连接AM.

①当m=3时，求AM的长；

②当AM=8时，求m的值；

③当m=1时，求∠MAO+∠BAO的度数.

挑战：

（4）若直线AB上有一点N（与点B不重合），满足S△AON= 6，试探究点N的坐标.

编题说明与教学手记：将勾股定理与平面直角坐标系关联起来，通过变换坐标的信息引导学生对应坐标的特点与线段之间的对应关系.从练习情况来看，学生在解（3）②时容易出现漏解，而解决（3）③时由于不能想到构造点M关于y轴的对称点，使得思路受阻.以下附我们讲评（3）③时使用的PPT截图（如图7）.

（3）已知点D（1，0），求∠DAO+∠BAO的度数.

图7

二、关于练习设计的两点随感

1.备课应该重视例、习题的设计，切忌随手“拿来主义”

以我们在教学一线所见，当前各级教辅资料、练习册、试卷集，包括很多学生报刊，上面的例、习题多是经由简单的复制、粘贴而来，而有些试题贴上所谓最新年度的中考题的标识，似乎就是一道新题，其实大多数的中考题都是陈题的低层次改编，如果备课过程中教师不加选择地直接拿来，缺少自己的专业设计与改编，缺少基于学情、教情的深度变式、必要重组，常常会使得习题训练的效果大大降低，使得减负增效成为一句空谈.我们认为，备课时除对教学环节、概念引领的情境创设等常规追求之外，还应该十分重视例、习题的改编设计.通过如上面提供的题例一样的增设铺垫、引导参与、注重关联等编题策略，使得例、习题更有利于自己的教学，真正做到减负增效.

2.设计练习时要注意系统开发，包括预设“跟进讲评”

钟启泉教授还指出：“所谓练习系统的开发有两层含义，一是强调练习的系统，即不是随心所欲、简单化的堆积，而是构成一种结构，一个阶梯；二是强调系统的开发，即不是零敲碎打，而是经年累月，作为一个网络来开发.”从上面提供的5个题例来看，我们比较注意这些试题的结构或阶梯；此外也想通过长期坚持下来，作为一个网络来研制，形成本校有特色的习题资源、校本资源库，从而丰富课程资源.特别是，以题5来说，我们还预设了“跟进讲评”，即通过制成如图7所示的PPT，渐次呈现启发式的提示语，追问学生的理解，将求解思路、关键步骤揭示出来，追求了“产婆术”的启发式习题教学.

参考文献：

1.钟启泉.读懂课堂［M］.上海：华东师范大学出版社，2015.

2.钟启泉.“批判性思维”及其教学［J］.全球教育展望，2002，31（1）.

3.刘东升.经历问题生成，深刻理解教材——人教八上“每日一题”的命题实践与思考［J］.中学数学（下），2014（4）.