运用数形结合思想，提高数学思维品质

☉江苏省无锡市南长实验中学　王宇峰



运用数形结合思想，提高数学思维品质

☉江苏省无锡市南长实验中学王宇峰

数学是揭示事物中数量与形体的本质关系与联系的科学.数学的两大研究对象“数”与“形”的矛盾统一是数学发展的内在因素，数形结合思想就是通过数与形之间的对立和转化来解决数学问题.正如华罗庚先生所说：“数缺形时少直观，形缺数时难入微”.数形结合思想从根本上来看包含两方面的内容，即“以形助数”和“以数解形”，巧妙地应用这一思想，不仅可以使问题变得更加简单和自然，而且还能培养学生全面研究问题的能力，培养严谨的数学思维和直观看待问题的能力.在初中数学教学中，如果教师能够有效运用数形结合思想来进行教学，那么就可以有效激发学生的学习兴趣，培养学生的数学思维能力，最终让学生提高数学品质.

一、运用数形结合思想，提高学生分析问题的意识

学生在平常生活中都会有一些图形方面的知识，积极利用学生的这些认识基础，将数与形相结合的方式转移到教学中来，从而在课堂上渗透相应的数形结合思想，并充分挖掘题目所提供的元素，提高学生分析问题的能力.

初三中考总复习时，笔者给学生出了这样一道题.如图1，已知A、B两点的坐标分别为（2，0）、（0，2），P是△AOB外接圆上的一点，且∠AOP= 45°，则点P的坐标为______.

图1

师：这是一个中考填空题，请大家仔细读题，分析并自行解决.

生1：首先确定圆心的坐标，然后通过勾股定理来解决.设Rt△AOB的斜边AB的中点为M，则M是△AOB外接圆的圆心.由题意可得∠BAO=30°，AB=4.如图2，连接PM、OM，则有PM=OM=AB，于是∠OPM=∠MOP=∠AOP-∠AOM=45°-30°=15°，OM=PM=2.

延长PM，作OT⊥PM，垂足为T，则∠OMT=30°.

在Rt△MOT中，由OM=2，∠OMT=30°，得OT=1，MT=，则PT=PM+MT=2+

过P作PH⊥x轴，垂足为H.

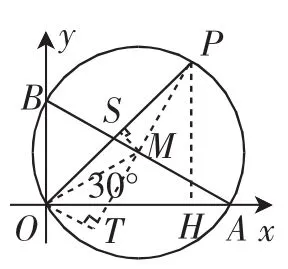
图2

师：在直角三角形中，通过勾股定理解决是我们的常见思路，生1的思路是可行的，但对计算能力的要求较高，尤其涉及二次根号下的配方，计算正确确实不容易.下面的同学一定有其他不同的解法，愿意和大家分享一下吗？

生2：我是通过解直角三角形的方法来解决的.如图3，作BS⊥OP、PH⊥x轴，垂足分别为S、H，连接PB.

由题意可知△BOS是等腰直角三角形.

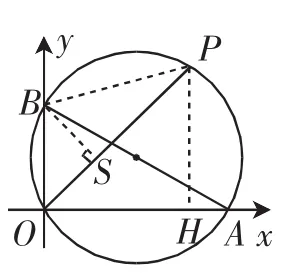
图3

师：生2在图形中发现了特殊的直角三角形，简化了计算过程，思路也更加清晰.

通过数形结合思想，立即激发了其他同学对试题进行再思考.在这样的氛围下，学生能够强化数形结合思想，逐步形成通过数形结合去分析问题、解决问题的思维方式.

二、运用数形结合思想，提高学生的转化迁移思维能力

数形结合思想是将数与形结合起来解决问题的一种思维方式.教师通过课堂教学问题的讲解，使学生充分理解数中有形，形中有数，数形是紧密联系的，用数形之间的对应关系，帮助并引导学生进行有效的数学转化，从而巧妙地解决一些看似复杂的数学问题.

2012年无锡市中考有这样一道题目：对于平面直角坐标系中的任意两点P1（x1，y1）、P2（x2，y2），我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离，记作d（P1，P2）.

（1）已知O为坐标原点，动点P（x，y）满足d（O，P）=1，请写出x与y之间满足的关系式，并在所给的直角坐标系（图4）中画出所有符合条件的点P所组成的图形；

图4

（2）设P0（x0，y0）是一定点，Q（x，y）是直线y=ax+b上的动点，我们把d（P0，Q）的最小值叫做P0到直线y=ax+b的直角距离，试求点M（2，1）到直线y=x+2的直角距离.

这是一道充分渗透应用数形结合思想的综合题，重点在第二问中.第二问中实际上是在点到点的直角距离的基础上引入点到线的直角距离.同样学生会根据第一问的方法先写出点到线的直线距离的表达式：d（M，Q）= |x-2|+|y-1|=|x-2|+|x+2-1|=|x-2|+|x+1|，接下来关键是要找到表达式的最小值.

有学生说：老师，我们可以通过第一问的方法，分类讨论化简表达式.

师：可以，这是一种比较直接的解答途径.还有其他方法吗？

学生窃窃私语.笔者接着引导学生思考：我们在讲绝对值的时候，它是怎么定义的？

生：绝对值是反映数轴上点与点之间的距离.这样学生就探索出这道题的内涵，笔者让学生通过画数轴，发现|x-2|+|x+1|这一表达式，实际上是表达：数轴上一点到2和-1的距离之和.这样学生很快就会发现|x-2|+|x+1|的最小值为3.

通过数形结合思想的运用，让学生将不同的知识元素进行类比迁移，激励学生的数学学习；可以更好地了解学生数学学习的历程，诊断学生在数学学习中遇到的困难，帮助学生认识自己在解题策略、思维方法或学习习惯上的长处和不足，及时调整和改善教与学的过程，这样可以帮助学生提高数学应用能力，开拓创新意识和实践能力，同时也自然而然地提升了应试的技能.

三、运用数形结合思想，深化学生综合运用知识的能力

教师在进行教学时，必须使学生明白要利用数形结合方法解决问题，就必须寻找两者的契合点，然后根据相应对象的属性将数与形进行巧妙地结合，通过对综合题目中各方面的知识点进行归纳总结，找到数、形之间的内在联系.

2015年山东日照的中考题：

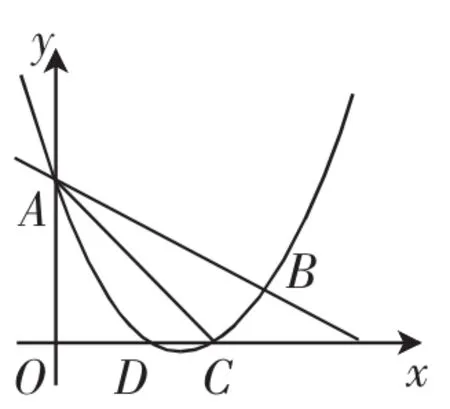
图5

（1）求抛物线的解析式和tan∠BAC的值；

（2）在（1）的条件下：①P为y轴右侧抛物线上一动点，连接PA，过点P作PQ⊥PA交y轴于点Q，问：是否存在点P，使得以A、P、Q为顶点的三角形与△ACB相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由.

②设E为线段AC上一点（不含端点），连接DE，一动点M从点D出发，沿线段DE以每秒一个单位的速度运动到E点，再沿线段EA以每秒个单位的速度运动到A后停止，当点E的坐标是多少时，点M在整个运动中用时最少？

分析：本题主要考查了运用待定系数法求抛物线的解析式、求直线与抛物线的交点坐标、抛物线上点的坐标特征、三角函数的定义、相似三角形的判定与性质、解一元二次方程、两点之间线段最短、轴对称的性质、矩形的判定与性质、勾股定理等知识.通过这题的解答，利用数形结合思想将数学中解直角三角形、函数、动点等知识综合运用，让每个学生对相应的知识能够做出清楚地判断，有利于学生学习能力的进一步发展，合理引导学生学会综合运用问题，掌握结论与条件的内在联系，令空间形式与数量关系巧妙结合，进而深刻感悟数形结合思想，全面掌握数形结合的科学应用.

数学是一门基础学科，其目的是教授学生一些基础性的知识，培养学生的思维能力、学习能力和解决生活实际问题的能力.初中数学教学的首要任务是培养学生的学习兴趣，进而激发学生的理性思维和责任感，所以在探寻教学的有效性方面需要进行深入思考和挖掘.数形结合的方法可以将抽象的数量关系具体化，把无形的解题思路形象化，这样有利于培养学生解题的灵活性、多样性和变通性，对于发展学生的思维能力起着积极推动作用.