利用压缩映像原理证明连续函数的介值性定理

莫海萍， 胡庆席（梧州学院信息与电子工程学院，广西梧州543002）



利用压缩映像原理证明连续函数的介值性定理

莫海萍， 胡庆席
（梧州学院信息与电子工程学院，广西梧州543002）

［摘 要］以压缩映像原理为工具，给出了闭区间上连续函数介值性定理的另一种证明．

［关键词］压缩映射；韦尔斯特拉斯逼近定理；中值定理

1　预备知识

连续函数的介值性定理［1］是数学分析中非常基本、非常重要的结论，本文以压缩映射原理［2］为主要工具，给出它的一个与众不同的证明．为此，先证明几个辅助性的结论．

命题1 设p是一个非零多项式，则p在任何一个非退化的有界闭区间［a，b］上都至多有有限个零点．

证 设多项式p的次数为m，则p（m－1）为一次多项式，在区间［a，b］上最多只有一个零点．运用反证法以及拉格朗日微分中值定理不难证明p在此区间上最多只有有限个零点．

命题2 设多项式p（x）在［a，b］上满足p（a）＜0，p（b）＞0，则存在α，β使得a≤α＜β≤b，以及

证 显然，多项式p′（x）为非零多项式，根据命题1的结论，多项式p′（x）在区间［a，b］上只有有限多个零点，记这些零点为x1，x2，…，xk，k可以等于零，这表示多项式p′（x）在［a，b］上没有零点．

令S＝｛a，b｝∪x1，x2，…，xk｛

｝，把S中的数排列为：c1＜c2＜…＜cl．显然，k≤l≤k＋2．设．记J最大值为t，则有p（ct）＜0，而p（ct＋1）≥0．

取α＝ct，β＝ct＋1，则在区间（α，β）上，p′处处不等于0，事实上，p′（x）＝0只在x1，…，xk处取得．根据达布定理，p′在区间（α，β）内不变号．在［α，β］上根据拉格朗日中值定理，存在c∈（α，β），使得

显然，从而，导数p′在（α，β）内处处为正．

命题3 设函数f∶［a，b］→R连续，则存在一个闭区间［m，M］以及一个一次函数g∶［a，b］→［m，M］，使得fg－1为由［m，M］到其自身上的连续映射．

证 记M和m分别为函数f的最大值和最小值，不失一般性，设m＜M，则函数的值域为［m，M］．不难看出，一次函数

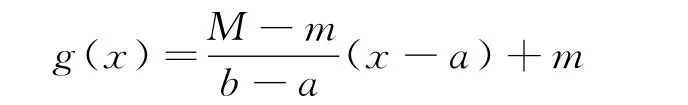
2　主要结论

定理1 设多项式f在［a，b］上满足f（a）·f（b）＜0，则在（a，b）上至少存在一点ξ，使得f（ξ）＝0．

证 不失一般性，假设f（a）＜0，f（b）＞0．则根据命题2，存在a≤α＜β≤b，使得f（α）≤0，f（β）≥0；并且对于区间（α，β）内的任意x，均有f′（x）＞0．如果f（α）＝0或者f（β）＝0，只需取ξ＝α或ξ＝β即可．

假设f（α）＜0且f（β）＞0．由于

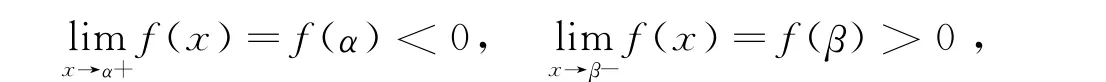
存在c，d，使得α＜c＜d＜β，满足

记f在区间［c，d］上的最小值和最大值分别为m和M，则有m＜0＜M．定义函数g∶［m，M］→［m，M］为

则

记g′在有界闭区间［m，M］上的最小值和最大值分别为q和Q，则显然0＜q≤Q．若q＝Q，则g′（x）在区间［m，M］为常值函数，函数f（x）为一次函数，存在零点是显然的．

设q＜Q．令

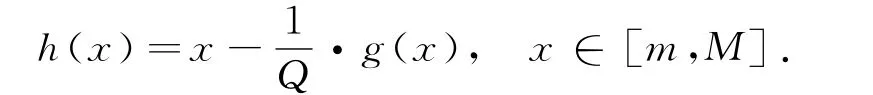
则

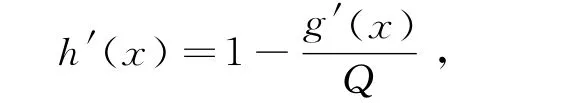
且有

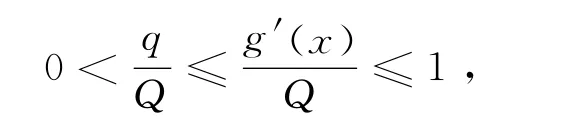
由此可知

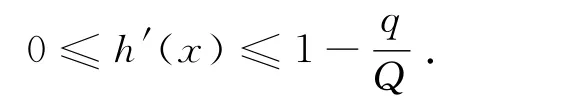
因此h在［m，M］上是单调递增的，于是h（m）≤h（x）≤h （M）．不难验证h（m）＞m，h（M）＜M，即函数h是由［m，M］到［m，M］的一个连续映射．并且有

所以，h∶［m，M］→［m，M］是压缩映射．从而，函数h在区间［m，M］上存在唯一一个不动点x0．根据是函数f在［a，b］上的零点．

现在给出闭区间上连续函数的零点定理的证明．

定理2 设f在区间［a，b］上连续，并且f（a）·f（b）＜0，则至少存在一点ξ∈（a，b），使得

证 不失一般性，假设f（a）＜0，f（b）＞0．根据韦尔斯特拉斯逼近定理［3］，存在一个多项式序列函数g，h的定义不难得出，点在［a，b］上一致收敛到f．

根据定理1，每个多项式fn都在区间（a，b）内有一个零点ξn，即fn（ξn）＝0，n＝1，2，…．显然，数列是有界数列，从而存在收敛子列．不失一般性，假设数列本身收敛，极限为ξ．设ε是任给的正数，有

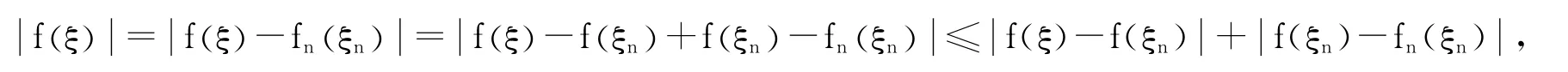
因为f在ξ点连续，存在整数M1，使得当n＞M1时，有

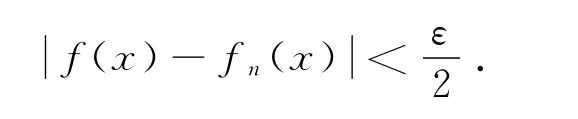
特别地，对于这些ξn，也有

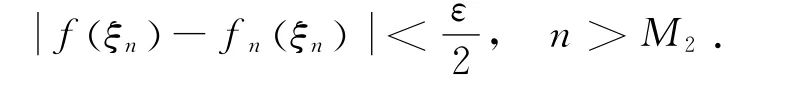
取M＝M1＋M2，则当n＞M时，有．所以

注 胡庆席为本文通讯作者．邮箱：huqxhu＠foxmail．com

［参 考 文 献］

［1］ Walter Rudin．Principles of Mathematical Analysis［M］．McGraw－Hill Science，1976．

［2］ Serge Lang．Real and Functional Analysis［M］．Springer，1993．

［3］ Bruckner，Andrew M．Differentiation of real functions［M］．American Mathematical Society，1994．

Proof by Contraction Mapping Principle of Intermediate－value Theorem of Continuous Functions

MO Hai－ping， HU Qing－xi
（School of Information and Electronic Engineering，Wuzhou University，Wuzhou Guangxi 543002，China）

Abstract：The intermediate－value theorem of continuous functions is proved by means of the principle of contraction mapping．

Key words：contraction mapping；Weierstrass’s approximation theorem；intermediate－value theorem

［基金项目］广西高校科研项目（201204LX372）

［收稿日期］2015－04－15

［中图分类号］O17

［文献标识码］C

［文章编号］1672－1454（2016）01－0088－03