严格的Hermite－Hadamard型不等式和Fejér型不等式

时统业， 尹亚兰， 周国辉（海军指挥学院信息系，南京211800）



严格的Hermite－Hadamard型不等式和Fejér型不等式

时统业， 尹亚兰， 周国辉
（海军指挥学院信息系，南京211800）

［摘 要］已有文献引入与Hermite－Hadamard不等式和Fejér不等式有关的单调函数．考虑这些函数与其上界和下界的差，利用二阶导数，给出这些差的上下界，建立了一些新的严格的Hermite－Hadamard型不等式和Fejér型不等式．

［关键词］二阶可微函数；凸函数；Fejér不等式；Hermite－Hadamard不等式；误差估计

1　引 言

本文约定d＝（a＋b）／2．

若f是区间I上的凸函数，则对任意a，b∈I，a＜b，下面的不等式成立

称为凸函数的Hermite－Hadamard不等式［1］．

1906年，Fejér推广了Hermite－Hadamard不等式，给出下面的Fejér不等式［2］

其中f是区间［a，b］上的凸函数，p（x）是区间［a，b］上正的可积函数且关于x＝d对称．

文［3－7］引入下面函数：

又记函数

定理A［3］设是凸函数，则H（t）是［0，1］上的凸函数且单调不减，对任意t∈［0，1］，有

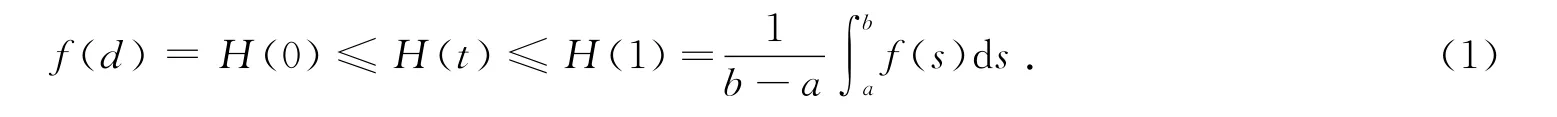
定理B［6］设是凸函数，则P（t）是［0，1］上的凸函数且单调不减，对任意t∈［0，1］，有

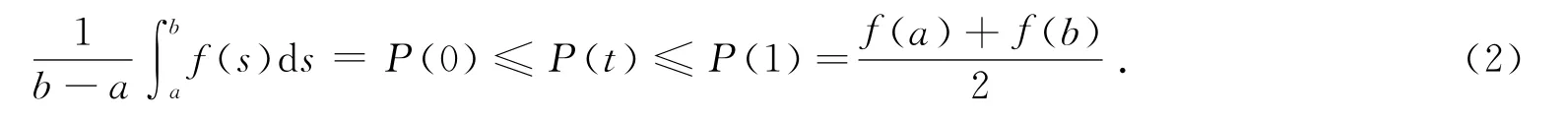
定理C［4］设是凸函数是正的可积函数，且关于x＝ d对称，则WH（t）和WP（t）是［0，1］上的凸函数且单调不减，对任意t∈［0，1］，有

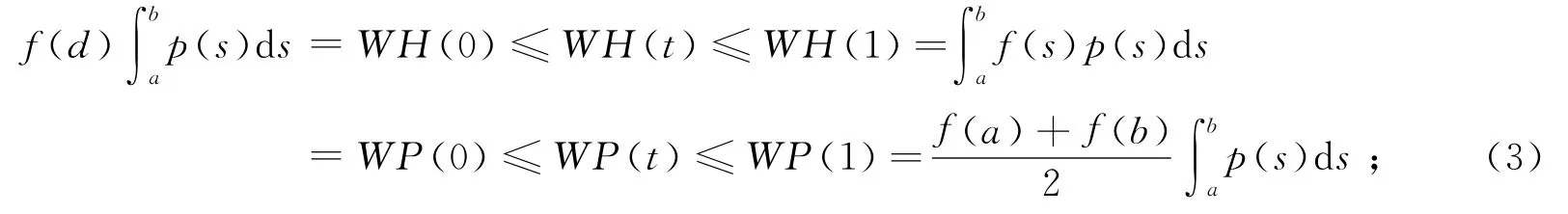
定理D［7］设是凸函数是正的可积函数，且关于x＝d对称，则I（t）和N（t）是［0，1］上的凸函数且单调不减，对任意t∈［0，1］，有

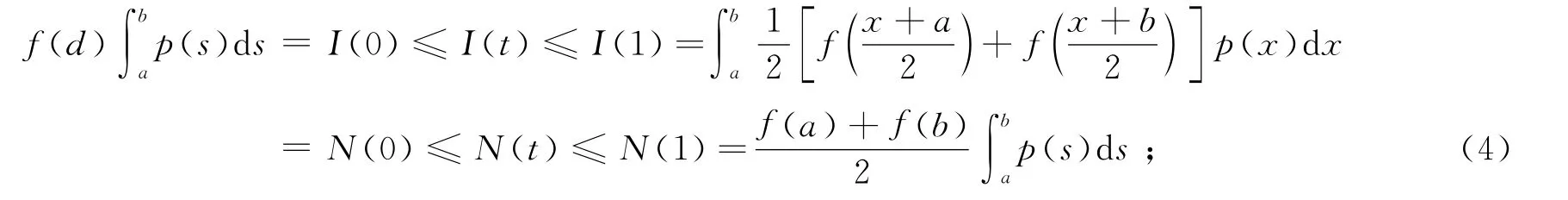
本文利用二阶导数，给出由式（1），（2），（3），（4）决定的差的上下界．

2　主要结果

证 考虑定义在［a，b］上的函数

则有

由Taylor定理，在x与d之间存在ξ使得

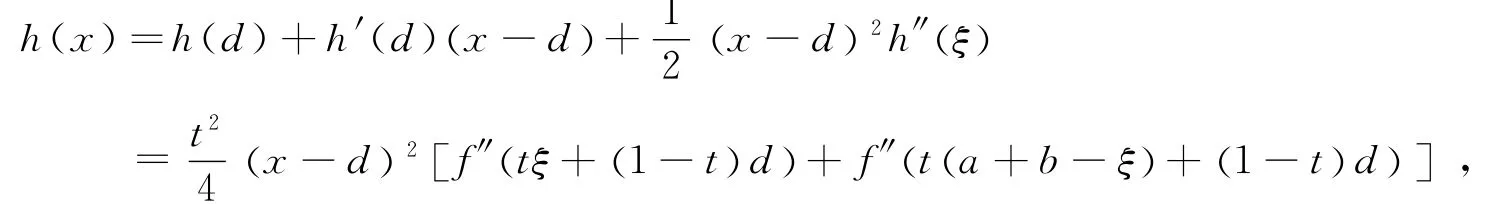
因m≤f"≤M，所以有

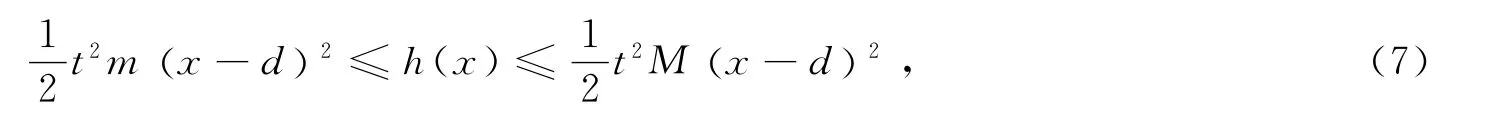
式（7）在［a，b］上对x积分得到式（5）．

考虑定义在［a，d］上的函数

利用Newton－Leibniz公式和变量代换得

当x∈［a，d］，u∈［x，tx＋（1－t）d］时，a＋b－2u≥0，因m≤f"≤M，所以有

上式在［x，tx＋（1－t）d］上对u积分得

也即

式（8）在［a，d］上对x积分得到式（6）．

注1 在定理1中取t＝0，则得到下面文［8］中关于中点积分公式的上下误差界的不等式

证 式（7）乘以p（x）然后在［a，b］上对x积分得式（9），式（8）乘以p（x）然后在［a，d］上对x积分得式（10）．

推论2．1 设条件同定理2，则有

证 在定理2的式（9）中取t＝1得证．

定理3 设条件同定理2，则对任意t∈［0，1］，有

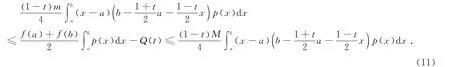
证

其中

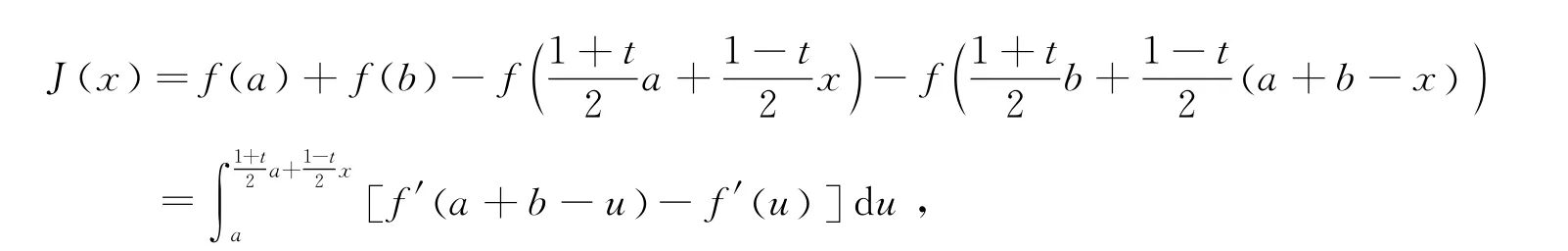
由式（12）、（13）得到式（11）的右端部分．同理可证（11）的左端部分．

推论3．1 设条件同定理1，则对任意t∈［0，1］，有

证 在定理3中取p（x）≡1得证．

推论3．2 设条件同定理2，则有

证 在定理3中取t＝0得证．

注2 在定理3中取t＝0，p（x）≡1，则得到下面文［9］中关于梯形积分公式的上下误差界的不等式：

定理4 设条件同定理2，则对任意t∈［0，1］，有

证 利用变量代换和p（x）的对称性得

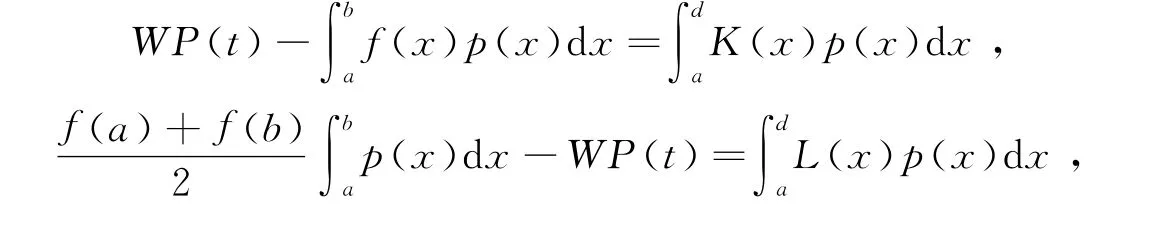
其中

以下的证明与定理3类似，故略去．

推论4．1 设条件同定理1，则对任意t∈［0，1］，有

证 在式（14）中取p（x）≡1得证．

定理5 设条件同定理2，则对任意t∈［0，1］，有

证

其中

以下的证明与定理3类似，故略去．

推论5．1 设条件同定理2，则有

证 在定理5的式（15）中取t＝1得证．

定理6 设条件同定理2，则对任意t∈［0，1］，有

证

其中

以下的证明与定理3类似，故略去．

推论6．1 设条件同定理2，则有

证 在定理6的式（16）中取t＝1得证．

注3 取f（x）＝x2，则本文定理和推论中的等号均成立．

［参 考 文 献］

［1］ Mitrinovi＇cD S．Analytic inequalities［M］．New－York：Springer－Verlag，Berlin：Heidelerg，1970．

［2］ Fejér L．Über die Fourierreihen，II，Math．［J］．Naturwiss，Anz．Ungar．Akad．Wiss．，1906（24）：369－390．

［3］ Dragomir S S．Two mappings in connection to Hadamard’s inequalities［J］．J．Math．Anal．Appl．，1992（167）：49－56．

［4］ Yang G S，Tseng K L．On certain integral inequalities related to Hermite－Hadamard inequalities［J］．J．Math．Anal．Appl．，1999（239）：180－187．

［5］ Dragomir S S，Miloševi＇aD C，Sándor J．On some refinements of Hadamard’s inequalities and applications［J］．Univ．Belgrad．Publ．Elek．Fak．Sci．Math．，1993（4）：3－10．

［6］ Yang G S，Hong M C．A note on Hadamard’s inequality．Tamkang．J．Math．，1997，28（1）：33－37．

［7］ Tseng K L，Hwang S R，Dragomir S S．Fejér－type inequalities（I）［J／OL］．Hindawi Publishing Corporation Journal of Inequalities and Applications，2010，Article ID 531976，7pages doi：10．1155／2010／531976．

［8］ Cerone P，Dragomir S S．Midpoint－type rules from an inequality point of view［M］．Handbook of Analytic－Computational Methods in Applied Mathematics，New York：CRC Press，2000：135－200．

［9］ Cerone P，Dragomir S S．Trapezoidal－type rules from an inequality point of view］M］．Handbook of Analytic－Computational Methods in Applied Mathematics，New York：CRC Press，2000：65－134．

Sharp Hermite－Hadamard Type Inequalities and Fejér Type Inequalities

SHI Tong－ye， YIN Ya－lan， ZHOU Guo－hui
（Department of Information，PLA Naval Command College，Nanjing 211800，China）

Abstract：Upper and lower bounds of the difference generated by monotone functions related to Hermite－Hadamard inequality and Fejér inequality are given by using the second derivative．

Key words：twice differentiable function；convex function；Fejér inequality；Hermite－Hadamard inequality；error estimation

［收稿日期］2014－12－29

［中图分类号］O178

［文献标识码］C

［文章编号］1672－1454（2016）01－0071－06