基于宽带信号的高精度时差估计算法

杨　健，郭　辉，陈　韵，曾德国，鲍成浩(中国航天科工集团8511研究所，江苏南京210007)



基于宽带信号的高精度时差估计算法

杨健，郭辉，陈韵，曾德国，鲍成浩
(中国航天科工集团8511研究所，江苏南京210007)

摘要:时差估计精度直接影响测向精度，传统时差估计算法受到采样时间间隔和解模糊算法的限制，无法进一步提高精度。对于宽带信号，通过时－频关系将时差估计转换为频率估计，继而采用基于时差搜索的离散傅里叶变换算法进行时差估计，其估计精度不受采样时间间隔的限制，能够适应较低信噪比。该算法运算简单，适于工程实现，可以实时进行处理。仿真结果表明，在一定的带宽条件下，该算法能达到较高的测向精度。

关键词:时差估计;宽带信号;频率估计;二分法

0　引言

随着雷达技术的不断发展，现代军用雷达发射的信号通常进行宽带调制，而线性调频是采用较多的调制方式。在电子侦察中，由于没有先验知识，一般采用宽带全向天线阵列来进行测向。对于远程到达的信号，主要利用信号到达不同天线的时间差来实现目标方位角的估计。对于装备的天线阵列，基线长度已经固定，那么测向精度主要受到时差估计精度的影响。因此，研究宽带高精度时差估计算法具有至关重要的意义。

很多学者对时差估计算法进行了研究，也取得了较多的成果。文献［1］给出在高信噪比条件下利用门限法进行信号到达时间估计方法，文献［2］研究了矩形包络正弦脉冲信号的到达时间估计算法，这些算法需要较高的信噪比，而且时差估计精度受到采样时间间隔的限制。文献［3］提出基于Haar小波到达时间估计方法，能够适当降低所需的信噪比，并有效提高时差估计精度。但是，时差估计精度仍然无法突破采样时间间隔的限制，在一定信噪比条件下，估计误差仍然大于一个采样间隔。由于两个天线阵元接收到信号的相位差与时差成正比关系，可以通过对相位差的估计间接得到时差的估计。但鉴相只能得到相位差在(－π，π)内的主值。当基线长度大于半波长时，可能出现相位模糊。相位解模糊有利用长短基线的解模糊［4-5］、基于互质数比基线长度的解模糊［6］等，但是这些算法运算量较大，工程实现成本较高，不适合实时进行处理，在单基线条件下无法进行解相位模糊。

本文针对宽带信号时差估计问题，提出了基于谱相关的宽带信号高精度时差估计算法。通过对两路天线接收到的信号进行频谱相关运算，将时差估计问题转换为频率估计问题，其精度不受采样时间间隔的限制，能够得到较高的时差估计精度。

1　信号模型

假设两个天线接收到的信号为:

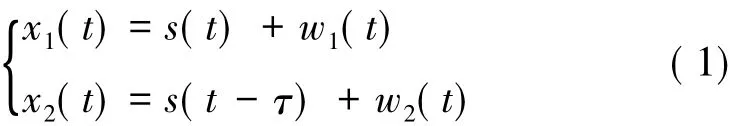
式中，τ为信号到达两个天线的时差; w1(t)、w2(t)为高斯白噪声，满足相互独立的要求，其均值为0，方差为σ2。

假设雷达发射的宽带信号为LFM信号，经数字采样后，其数学表达式为:

式中，Am为信号幅度; fc为信号载频; k为信号调频斜率，那么信号带宽B=kT，T为脉冲的宽度; N为信号的样本点数。Δt为采样时间间隔，即Δt= 1/fs，fs为采样频率。

2　高精度宽带信号时差估计算法

2．1基于谱相关的时差估计

对天线接收到的两路时域信号作离散傅里叶变换，得到两路频谱信号:

式中，S(k)为信号s(t)的离散傅里叶变换; W1(k)、W2(k)为噪声w1(t)、w2(t)的离散傅里叶变换; D为量化时差，即D=τ/Δt。

将X1(k)与X2(k)共轭相乘，那么得到新的信号为:

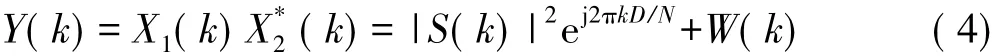
式中，W(k) = W*2(k) S(k) +W1(k) S*(k) ej2πkD/N+ W1(k) W*2(k)。

由式(4)可知，Y(k)可以看作是一个幅度为|S(k) |2、频率为D、采样间隔为1/N、宽度为原始信号s(t)带宽的正弦波。那么根据时域与频域的相对关系，可以将时差估计问题转换为正弦波频率估计问题［7］。

2．2频率估计算法

在工程应用中，频率估计算法不仅需要较高的精度，而且需要较好的实时性，主要算法有利用信号谱线特性进行频率估计和利用相位差分进行频率估计。基于信号谱线特性的频率估计算法有Rife算法［8-9］等，性能主要受到FFT的量化频率间隔限制。基于相位差分的频率估计算法有Kay提出的利用相位加权法［10］等，算法所需的信噪比较高，而且如果进行相位差分的数据混有噪声，对频率估计精度的影响就较大。

本文提出基于时差搜索的离散傅里叶变换算法，算法原理如下:

由式(4)可知，通过变换:

式中，fk为第k根谱线的频率值，fk=fsk/N。

构造信号:

式中，W'(k) = W(k) Z(k)。

由式(7)可知，搜索不同的τ'使| T(τ') |的值最大，那么此时的τ'就是时差估计值τ。

2．3二分法与初始搜索值

利用该算法进行时差估计，需要对时差值进行一维的搜索。在实际工程实现过程中，一维搜索需要较多的运算，也消耗大量的处理时间。因此，为了增加算法的实时处理能力，采用二分法进行时差搜索，从而减少运算量与处理时间。

二分法进行时差搜索如图1所示，横坐标为时差值τ'，纵坐标为|T(τ') |。

式中，τ'为搜索的时差值。

那么，联合式(5)和式(6)，得到:

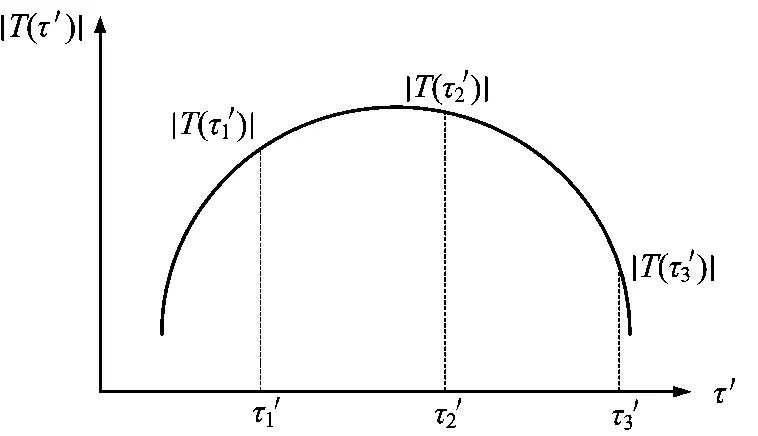
图1　二分法时差搜索示意图

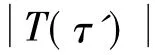
2)时差搜索N次后结束搜素，N的大小视工程所需时差精度而定。

由测向原理可知［11］，信号到达两个天线的时差为:

式中，L为两个天线之间的距离，即基线长度;θ为信号的波达角; c为电磁波传播速度。

由式(8)可知，信号到达两个天线的时差最大值满足以下条件:

因此，可以选取－L/c和L/c作为时差搜索的初始值。

2．4带宽估计

在实际工程中，由于信号具有有限带宽，利用的整个频谱信号中必然混有噪声。因此，为了进一步提高时差估计精度，需要对信号进行带宽估计，选取有效的谱线进行运算。

由式(4)可知，噪声W(k)的功率为:

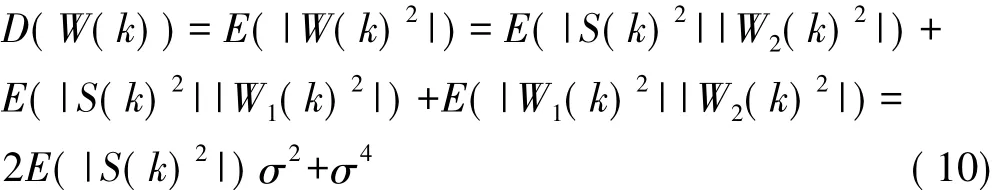
假设E(| S(k) |2) = a2，那么Y(k)的信噪比SNRY为:

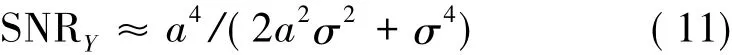
噪声的能量是均匀分布在整个频段，而信号能量却只是集中在有限的带宽内。因此，经过提取信号有效带宽后，信号的能量没有损失，而噪声的能量却损失为原来能量的B/fs。那么，经过带宽提取后，Y(k)的信噪比为:

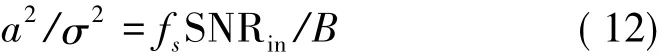
式中，SNRin是输入信号s(t)的原始信噪比。

将式(12)代入式(11)，可得:

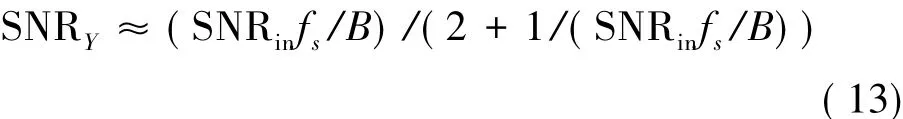
因此，通过信号带宽提取可以有效提高信号Y(k)的信噪比，从而提高时差估计精度。

3　算法仿真与分析

设置采样频率fs=500MHz，起始频率fc=100MHz，信号带宽B=50MHz，信号长度T=3μs，信号到达两个天线的时差τ=3ns，信噪比在［1dB，10dB］范围内以1dB为步进。采用Harr小波的到达时间估计算法和本文基于谱相关的时差估计算法，各进行300次蒙特卡洛实验，两种算法的时差估计精度对比如图2所示。

图2　Harr小波与谱相关算法性能对比图

由图2可知，Harr小波的到达时间估计算法受到采样时间间隔的限制，在较低信噪比条件下，时差估计精度较差。在高信噪比条件下，时差估计精度也在一个采样间隔左右。基于谱相关的时差估计算法，经过谱相关后将时差估计问题转化为频率估计问题，突破了采样时间间隔的限制。在信噪比1dB的情况下，时差估计的均方根误差小于0．4ns，远小于采样时间间隔2ns。

在以上条件下，经过谱相关后，采用Rife算法、Kay算法和时差搜索算法进行时差估计，两种算法的时差估计精度对比如图3所示。

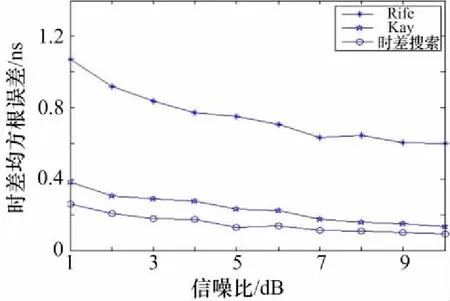
图3　Rife算法、Kay算法和时差搜索算法性能对比图

由图3可知，在Rife算法、Kay算法和时差搜索算法三种算法中，时差搜索算法的性能最好。Rife算法受到FFT的量化频率间隔限制，精度较差。Kay的相位加权法在低信噪比条件下与时差搜索算法的精度有一定的差距。在信噪比提高的过程中，Kay算法性能接近时差搜索算法。

采用基于谱相关的时差搜索算法，信号到达两个天线的时差τ= 2．5ns，带宽取30MHz、50MHz和80MHz，各进行300次蒙特卡洛实验，不同带宽条件下的时差估计精度如图4所示。

由图4可知，时差搜索算法受信号带宽的影响，信号带宽越大，时差估计精度越高。该算法在低信噪比条件下，也能达到较高的时差估计精度。

图4　不同带宽下时差搜索算法性能图

4　结束语

测向本质上是时差估计，因此研究高精度时差估计算法可以进一步提高测向精度。对于宽带信号，本文采用基于谱相关的方法将时差估计问题转换成频率估计算法，通过二分法进行时差搜索，继而得到高精度的时差估计值。由仿真分析可知，算法所需信噪比较低，可以突破采样时间间隔的限制。该算法运算简单，便于工程实现，具有较高的实用性，可以广泛应用于电子侦察设备。

参考文献:

［1］Ho KC，Chan YT，Inkol R．Pulse arrival time estimation based on pulses ample ratios［C］∥IEEE Proc．of Radar Sonar and Navigation，1995(4) : 153－157．

［2］Chan YT，Lee BH，Inkol R，et al．Detection and arrival time estimation of a pulsed sinusoid［C］∥IEEE Communications， Computers and Signal Processing，2005(8) : 37－40．

［3］胡国兵，刘渝，邓振淼．基于Haar小波变换的信号到达时间估计［J］．系统工程与电子技术，2009，31(7) : 1615 －1619．

［4］Macphie RH．Thinned coincident arrays for the direct measurement of the principal solution in radio astronomy［J］．IEEE Trans．on Antennas Propagation，2003，51 (4) : 788 －793．

［5］Macphie RH，Tae HY．On using the compound interferometer to obtain the power pattern of a conventional receiving array［J］．IEEE Trans．on Antennas and Propagation，2009，10(57) : 3356 －3359．

［6］龚享铱，袁俊泉，苏令华．基于相位干涉仪阵列多组解模糊的波达角估计算法研究［J］．电子与信息学报，2006，28 (1) : 55－59．

［7］Bai YC，Zhang XG，Tang L．Subsample time delay estimation based on phase spectrum of band limited stochastic signals ［J］．Journal of Nanjing University of Aeronautics＆Astronautics，2010，27(2) : 170－175．

［8］Rite DC，Boorstyn RR．Single-tone parameter estimation from discrete-time observations［J］．IEEE Trans．on Information Theory，1974，20(5) : 591－598．

［9］司伟建，郝鑫，赵忠凯，等．基于改进的Rife测频算法及其FPGA实现［J］．弹箭与制导学报，2012，32(1) : 205－207．

［10］Steven K．A fast and accurate single frequency estimator［J］．IEEE Trans．on Acoustics Speech and Signal Processing，1989，37(12) : 1987－1990．

［11］杨健，刘渝，狄慧．基于时差校正的长基线宽带测向算法研究［J］．系统工程与电子技术，2013，35(1) : 20－28．

High-precision time delay estimation algorithm of wideband signal

Yang Jian，Guo Hui，Chen Yun，Zeng Deguo，Bao Chenghao
(No．8511 Research Institute of CASIC，Nanjing 210007，Jiangsu，China)

Abstract:The precision of direction finding is affected directly by the precision of time delay estimation．Traditional time delay estimation algorithms are limited by the requirement of unwrapping phase ambiguity and sample interval．So the precision of time delay estimation can not be improved．The wideband signa according to the relationship between time domain and frequency domain，converts time delay estimation into frequency estimation．Then，the time delay can be estimated by the discrete Fourier transform based on the search of time delay．The precision of this algorithm is not limited by the sample interval and the algorithm is able to adapt to the low signal-to-noise ratio．The algorithm is simple and suitable for engineering implementation．It can be carried out in real time processing．The simulation results show that the algorithm can achieve very high precision of time delay on the condition of certain band width．

Key words:time delay estimation; wideband signal; frequency estimation; dichotomy

作者简介:杨健(1986－)，男，博士研究生，主要研究方向为雷达信号处理、电子侦察。

收稿日期:2015－10－10; 2015－12－30修回。

中图分类号:TN911．23

文献标识码:A