基于多边形接触模型的内电车钩建模研究

邹瑞明， 张志超， 马卫华

(1. 西南交通大学 牵引动力国家重点实验室，四川 成都 610031； 2. 中国铁道科学研究院 机车车辆研究所，北京 100081)

钩缓装置在起到机车车辆间连接、牵引和缓冲作用的同时，对机车车辆的运行安全性也有较大程度的影响，这一点对于重载列车显得尤为突出。重载列车的编组数量和牵引质量相对普通列车要大得多，由于牵引制动、线路条件等因素的影响，其纵向冲动也要大得多。纵向冲动恶化了钩缓装置的工作环境，易引发钩缓装置的疲劳失效，进而导致脱钩、断钩等安全事故[1]。为了改善重载列车的运行安全性，降低钩缓装置带来的风险隐患，不少学者针对钩缓装置的强度、疲劳以及工艺设计的改进等方面做了大量的研究工作，也取得了较为显著的成效[2]。然而，通过对近年来重载列车安全事故的调查研究表明，钩缓装置的偏转行为对于机车车辆动力学也存在较大的影响，过大的纵向压钩力容易导致车钩发生压屈失稳，并在车钩处产生较大的横向分力，而这部分横向分力最终通过机车车辆的悬挂系统传递到轮对上，借助轮轨力来与之平衡，引发异常大的轮轨横向力，导致扩轨掉道，甚至脱轨倾覆等重大安全事故[3-6]。因此，为了明确钩缓装置在承压时的动态响应及其对机车车辆动力学性能的影响，钩缓装置的稳钩能力及其动力学模型的建立成为近些年的热门话题，通过这些研究过程，钩缓装置的动力学模型也一步一步地得到了改善[7-13]。

罗世辉针对重载机车钩缓装置的结构特点和稳钩原理进行了深入的分析，在此基础上建立了考虑车钩自由转角与钩肩特性的钩缓装置动力学模型，并运用该模型分析了重载试验中出现的机车脱轨问题[4]，但是此模型的缓冲器是通过刚度特性进行模拟，并未考虑缓冲器的非线性迟滞特性；马卫华则进一步考虑了从板的纵向自由度，并采用了片段线性化的缓冲器特性，通过该模型分析了SS3B型电力机车在长大下坡道上的稳钩能力，指出采用13号车钩的SS3B型电力机车在30‰下坡道上所能承受的最大压钩力为1 100 kN左右[9-10]；吴庆和许自强在以上二人的工作基础上进一步完善了钩缓装置的动力学模型，不仅建立了具有非线性迟滞特性的缓冲器模型，而且通过融合摩擦力元和钩肩、止挡特性建立了具有通用性的钩缓装置结构模型[11-13]。但这种模型用以模拟内电车钩还存在值得改进之处，首先，钩尾框在车钩箱中有少许活动空间，钩尾销也因而具有一定的活动范围，所以将车钩的转动中心固定于钩尾销处是值得商榷的；其次，钩尾摩擦弧面处的摩擦力是采用缓冲器的回复力作为法向力，取一固定长度作为力臂，通过摩擦转矩的形式施加于钩尾处进行模拟，未能表现出钩尾处的弧面-弧面接触摩擦特性；最后，其钩头连挂面处也是分别采用摩擦力矩和垂向摩擦力模拟车钩连挂面处的水平摩擦力和垂向摩擦力，也未能表现出钩头连挂面间的曲面-曲面接触摩擦特性。

本文在详细分析了内电车钩结构特性和稳钩原理的基础上建立了内电车钩的动力学模型，其中钩尾处的弧面-弧面接触和钩头连挂面间的曲面-曲面接触都首次采用了多边形接触模型，相对传统动力学模型而言，能够更为真实地反应内电车钩在不同工况下的动态响应，同时还能够模拟连挂钩头间的垂向窜动和跳钩等问题，相对有限元接触模型而言，又具有更高的计算效率。

1 多边形接触模型

在计算多体系统动力学中，通常将接触问题简化为点与点之间的相互作用，这种方法虽然得到了较为广泛的应用[14]，但是采用单点接触分析接触问题毕竟存在一定的局限性，并且对于复杂曲面出现多点接触甚至共形接触时，接触点的确定存在一定的难度；另外一种求解精度较高的有限元分析方法(FEA)所需计算代价过大。多边形接触模型则可视为是点接触方法和有限元法之间的一个折中，即刚体表层采用多边形建模，借助多边形判定接触区域并对接触区域进行离散化处理，最后通过弹性基础模型对接触力进行求解，这种接触算法与计算机图形学密切相关[15]。

多边形建模是一种常见的建模方式，模型的几何外形主要由节点和多边形组成，其中节点位置通过欧几里得空间位置坐标进行定义，多边形则由各节点组成，模型的几何外形可通过所有多边形的拓扑关系进行确定。

假设刚体表面由一层厚度为b的薄弹性层覆盖，接触力则可以通过弹性基础模型进行求解，若忽略弹性层中的切向应力，其法向位移un和压力pn之间的关系为

( 1 )

式中：K为材料的弹性模量，对于泊松比ν<0.45的线弹性层，其弹性模量K为

( 2 )

其中，E为材料的杨氏模量。对于匀质弹性体而言，其接触刚度k为

( 3 )

两接触体之间的接触刚度ke可视为两弹性体接触刚度的串联

( 4 )

则第i个接触单元的法向接触力Fni为

Fni=keAeiuni

( 5 )

式中：Aei为该接触单元所对应的有效接触面积；uni为该接触单元的压入深度。

另外，接触单元的切向力则由其法向接触力Fni和切向相对速度vti决定

( 6 )

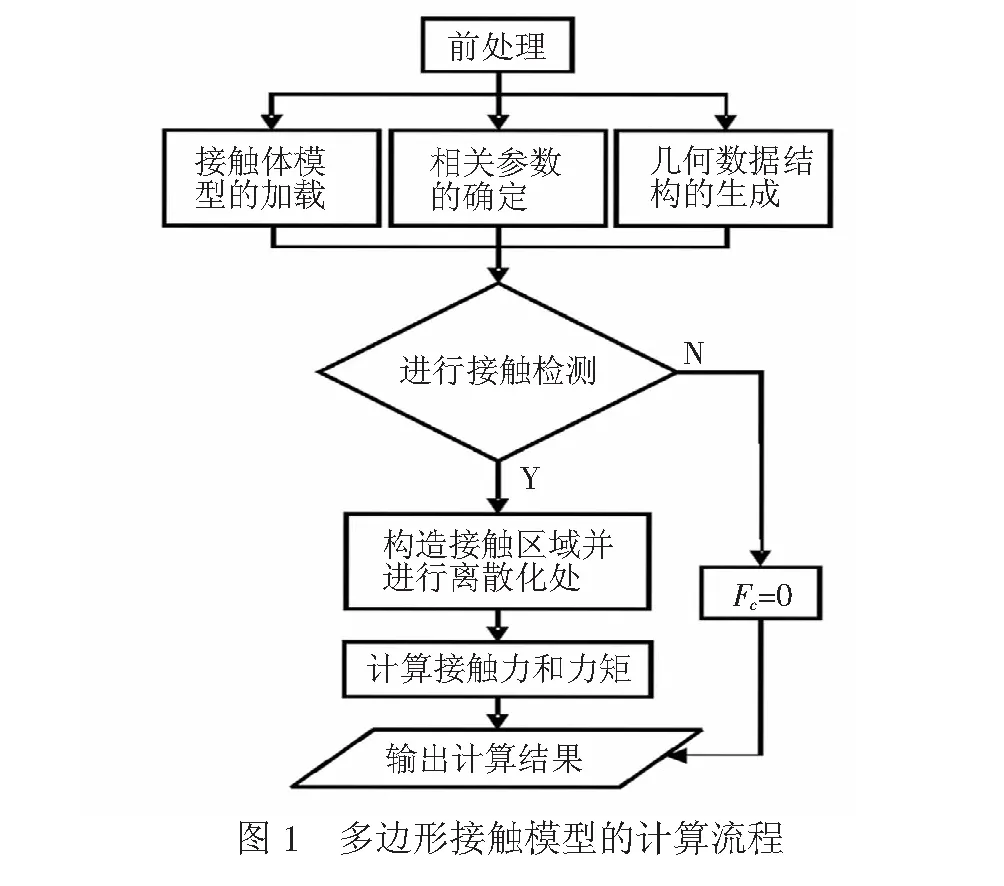
式中：μ为摩擦系数；vf为静摩擦临界速度。两接触体间的接触力可根据所有接触单元法向力和切向力的矢量和进行求解。图1为多边形接触模型的计算流程。

2 内电车钩的结构特性

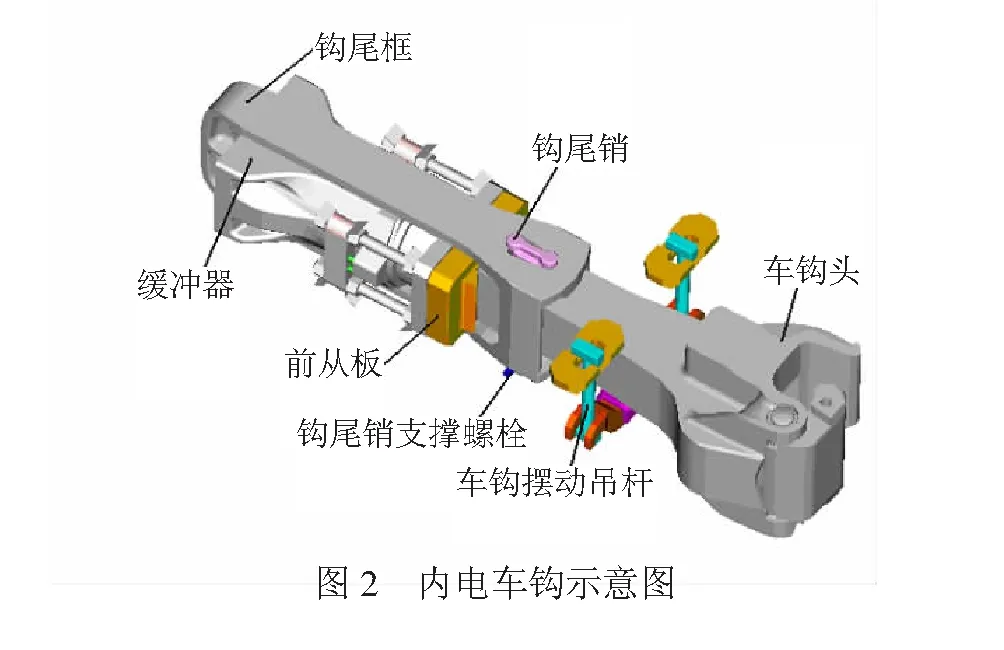
本文采用的内电车钩符合文献[16]标准，其结构组成见图2，它可与其他国产机车、货车实现整套互换或缓冲器单独互换，具有标准化程度高、运用检修方便等特点。当车钩受拉时，力传递顺序为：钩头-钩尾销-钩尾框-缓冲器-前从板-底架，在此过程中，车钩带动扁销自动卡位进入钩尾框梨形孔的尖端，从而实现自动对中；当车钩受压时，力传递顺序为：钩头-钩尾圆弧面-前从板圆弧面-缓冲器-底架，在此过程中，钩尾销和钩尾框基本上不承受纵向压力，但钩尾销与钩尾框上的梨形孔相配合可起到限制车钩发生过大偏转的止档作用。同时也能看出，不论车钩是受压还是受拉，缓冲器都处于压缩状态，因而具有相同的拉压特性。

3 内电车钩稳钩原理研究

内电车钩的钩尾弧面和前从板弧面间在纵向压力的作用下存在接触摩擦，如果两弧面间有相对运动或相对运动的趋势，就在弧面间产生相应的动摩擦力或静摩擦力，而这个摩擦力便是车钩稳钩力矩的来源，起到阻止车钩发生偏转的作用，见图3。

由于钩尾框在车钩箱中具有一定的转动自由度，根据文献[17]的分析，在缓冲器自由状态下钩尾框有将近2°的偏转，在车钩拉动钩尾框至缓冲器最大行程83 mm时，其转角甚至可达5°，钩尾销随钩尾框的转动也具有一定的活动空间，因此从严格意义上来说，车钩的转动中心并不固定在某一处，另外，钩尾摩擦弧面与从板摩擦弧面的半径并不相同，在钩尾接触面的摩擦力尚未达到饱和之前，两弧面之间的运动关系应为纯滚动，其接触点位置沿着圆弧面移动，因而在钩尾接触面发生相对滑动之前，车钩的转动中心应位于钩尾摩擦弧面与从板摩擦弧面的接触点处。

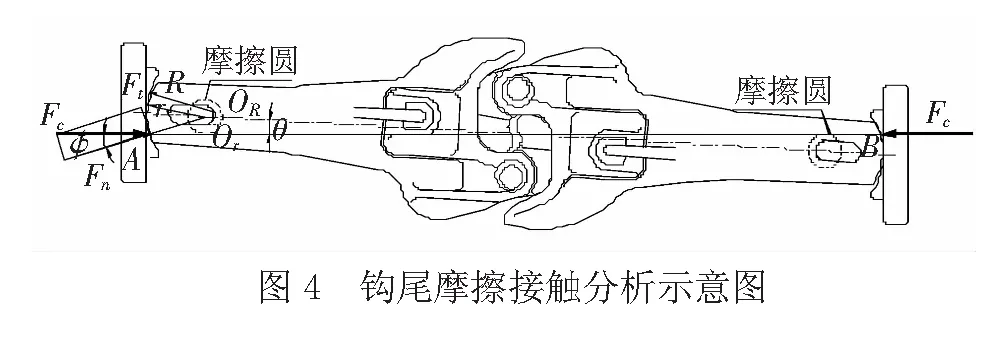
图4为车钩尾端与前从板圆弧面接触摩擦分析示意图，前从板圆弧面圆心为OR，半径为R，钩尾圆弧面圆心为Or，半径为r，车钩转角为θ。分别过两端钩尾圆弧面的圆心作摩擦圆，其半径Rf=rsinφ，其中φ为摩擦角，根据摩擦圆理论，两端接触点之间的连线AB应与摩擦圆相切，同时连线AB亦可视为连挂车钩间的传力线，当车钩处于稳钩状态时，车钩并不会对车体产生额外的横向分力，所以其传力线应与车体中心线平行，假设钩尾与从板间处于滚动摩擦与滑动摩擦之间的临界状态，可得出以下关系式

( 7 )

式中：Lp为车钩受压时，钩尾摩擦弧面的圆心至车钩连挂中心线的距离。

通过式( 7 )可求得内电车钩临界状态下的车钩转角θ为

( 8 )

由式( 8 )可知，内电车钩的稳钩能力主要取决于钩尾的摩擦状态，表1所示为理论上不同钩尾摩擦系数所对应的车钩临界转角，当车钩转角低于临界值时，车钩处于稳钩状态，但是由于轨道不平顺的存在，两车体间存在横移和摇头运动，所以实际上车钩传力线与车体中心线并不会保持绝对平行，而是处于一个动态的调整过程，随着纵向压钩力的增大，车体间的相对错位也会有所增大，同时导致车钩转角的增大，一旦车钩转角超出临界转角，在纵向压钩力的作用下，钩尾处开始出现滑动，车钩转角大幅增大，其产生的横向分力也会对机车动力学性能带来一定的负面影响。

表1 不同摩擦系数下的临界转角

4 内电车钩动力学模型的建立

4.1 车钩建模研究

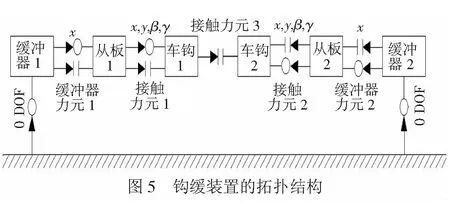
图5所示为一对连挂内电车钩动力学模型的拓扑结构图，模型共由2个车钩、2个从板和2个缓冲器组成，其中缓冲器固连于车体上，由于缓冲器具有相同的拉压特性，因此这里忽略钩尾框的建模，将其与从板视为一体，相对缓冲器具有纵向(x方向)自由度，2车钩分别与从板相连，具有纵向(x方向)、横向(y方向)和绕铅垂轴(z方向)转动的自由度，其转动中心位于接触弧面上，并根据内电车钩的结构特性辅以相应的止档力元，另外，钩尾处和连挂钩头处的接触摩擦问题采用多边形接触模型建立，车钩与从板的多边形网格见图6，其中车钩由3 160个多边形组成，从板由1 184个多边形组成，其结构外形均根据实际尺寸建立，在接触面处的网格较细，能够较好的保证计算精度。

4.2 缓冲器数学模型

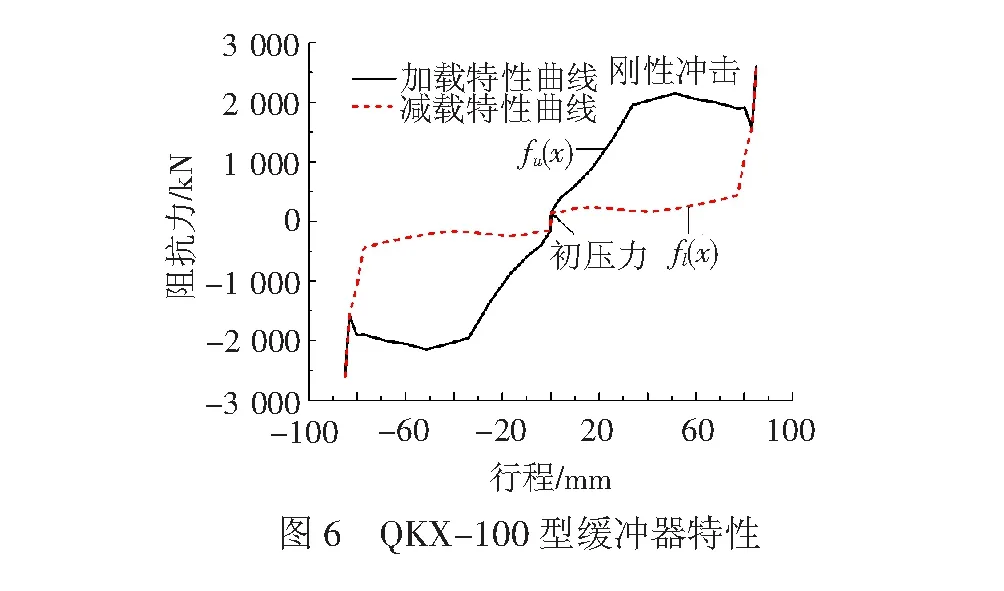
考虑到缓冲器所具有的非线性迟滞特性，本文主要根据QKX-100型缓冲器落锤试验得出的特性曲线，分别建立以缓冲器行程为变量的加载特性曲线fu(x)和减载特性曲线fl(x)，见图6，缓冲器阻抗力可以由表征刚度特性的弹簧力和表征迟滞特性的迟滞力组成，其中某一特定行程x下的弹簧力fk可以定义为

( 9 )

为了保证函数在加载特性和减载特性间切换的连续性，在迟滞力中引入切换速度ev，这样迟滞力fhys可定义为

(10)

式中：Δv为缓冲器两耦合连接点的相对速度，引入符号函数sign(Δv·x)，可以得到缓冲器的数学模型

FB=

5 内电车钩动力学模型的验证

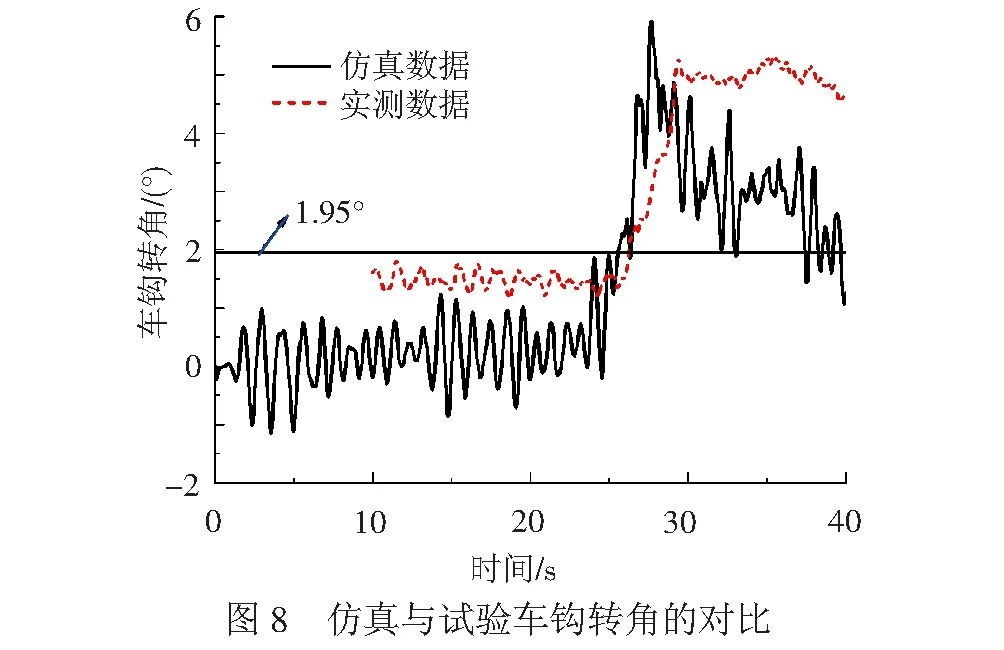
为了验证该模型的正确性，本文建立了SS4B型电力机车的动力学模型，模型中两台相同的4轴机车通过该内电车钩动力学模型进行连挂，从而组成八轴机车，同时提取某重载线路综合试验中列车紧急制动工况下的压钩力，见图7(注：5～10 s为过渡段)，并施加在连挂机车的动力学模型上进行仿真计算，轨道不平顺采用美国五级谱，机车运行速度与试验中列车制动初速一致，为70 km/h，通过对比分析仿真结果与相应的实测数据来验证该内电车钩动力学模型的正确性。通过对实测数据的分析可知，车钩大致在1.95°左右发生失稳，根据式( 8 )可逆推出钩尾摩擦系数大致在0.19，因此仿真模型中的钩尾摩擦系数也取为0.19。

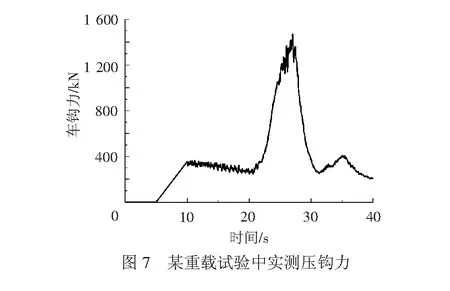
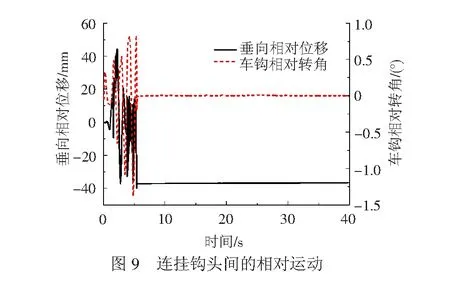
图9所示为仿真车钩转角与实测车钩转角的对比情况，从中能够看出，仿真结果与实测结果在整体上具有一定的相似度，当车钩转角达到1.95°后将产生较大幅度的偏转，这也印证了前面的理论分析，值得注意的是车钩的最大转角并不是出现在压钩力最大的时刻，而是出现在压钩力开始减小的阶段。当车钩转角达到最大值时出现了一个峰值，这是由于车钩在失稳后促使车体发生摇头或横移，并在二系横向止档处产生冲击所引起的。另外，由于摩擦力总与运动方向相反，因此即便当压钩力减小后，内电车钩也不会及时复位，试验数据显示车钩在偏转后的转角持续稳定在5°左右，而仿真结果则总体呈现减小趋势，这主要是由于车体的稳钩特性引起的，仿真相对试验而言有一定的局限性，参数设置上也存在一定的差异。图9所示为连挂车钩钩头处的相对转角和垂向相对位移，在车钩承压之前，2钩头间具有一定的相对运动，但在承压后，2钩头间表现出了较好的稳定性，钩头间几乎不会发生相对偏转，垂向相对位移稳定在37 mm左右，就整体上而言，该钩缓装置动力学模型还是能够较好地模拟内电车钩的动态行为，包括2连挂钩头间的相对运动。

6 结论

(1) 根据摩擦圆理论可知，内电车钩的稳钩能力主要取决于钩尾的摩擦状态，当车钩转角小于临界值时，车钩处于稳钩状态，一旦车钩转角超出临界值，在纵向压钩力的作用下，钩尾处开始出现滑动，车钩也将发生失稳；

(2) 相对传统模型而言，基于多边形接触模型而建立的内电车钩进一步考虑了钩尾处弧面-弧面以及连挂钩头间曲面-曲面的接触摩擦特性，能够更为准确地反映内电车钩在不同工况下的动态行为；

(3) 通过与线路试验数据的对比分析可知该模型具有较好的可靠性，同时，该模型还能够用于模拟连挂钩头间的垂向窜动和跳钩安全性等问题。

参考文献：

[1] 李伟. 长大重载列车断钩事故的思考[J]. 铁道机车车辆，2005，25(2)：50-51.

LI Wei. Reflect on the Coupler Breakage Accidents of Heavy-Haul Train[J]. Railway Locomotive & Car，2005，25(2)：50-51.

[2] Noughabi SMMZ，Dehghani K. Failure Analysis of Automatic Coupler SA-3 in Railway Carriages[J]. Engineering Failure Analysis，2007，14(5)：903-912.

[3] 中国铁道科学研究院. HXD2机车DFC-E100车钩1+1牵引万吨组合列车试验报告[R].北京：中国铁道科学研究院机车车辆研究所，2008.

[4] 罗世辉，封全保，杨俊杰. 承受纵向压力时HXD2型重载机车动力学问题研究[J]. 铁道机车车辆，2008，28(S): 145-149.

LUO Shihui，FENG Quanbao，YANG Junjie. Research on Dynamics of the HXD2 Heavy-load Locomotive Bearing Longitudinal Compressive Strength[J]. Railway Locomotive & Car，2008，28(S)：145-149.

[5] Transportation Safety Board of Canada. Railway Investigation Report R02C0050[R]. Ottawa：TSB Canada，2002.

[6] Australian Transport Safety Bureau. Derailment of train 3DM4 near Manton Dam NT[R]. Australia：Australian Transport Safety Bureau，2008.

[7] 王开云，翟婉明，封全保，等. 重载机车车钩自由角对轮轨动态安全性能的影响[J]. 中国铁道科学，2009，30(6)：72-76.

WANG Kaiyun，ZHAI Wanming，FENG Quanbao，et.al. Effect of the Coupler Free Angle on Wheel/Rail Dynamic Safety Performance of Heavy Haul Locomotive[J]. China Railway Science，2009，30(6)：72-76.

[8] 阳光武，肖守讷，马卫华. 制动力对机车直线运行安全性的影响[J]. 西南交通大学学报，2010，45(5)：657-662.

YANG Guangwu，XIAO Shoune，MA Weihua. Effect of Coupler Compression Force on Locomotive Safety on Tangent Track[J]. Journal of Southwest Jiaotong University，2010，45(5)：657-662.

[9] MA Weihua，LUO Shihui，SONG Rongrong. Coupler Dynamic Performance Analysis of Heavy Haul Locomotives[J].Vehicle System Dynamics，2012，50(9)：1 435-1 452.

[10] 马卫华，杨俊杰，罗世辉，等. SS3B型电力机车长大下坡道稳钩能力分析[J]. 铁道学报，2010，32(2)：109-113.

MA Weihua，YANG Junjie，LUO Shihui，et al. Study on the Coupler Stability of Locomotive SS3B Running on the Long Heavy Down Grade[J]. Journal of the China Railway Society，2010，32(2)：109-113.

[11] WU Qing，LUO Shihui，XU Ziqiang，et al. Coupler Jackknifing and Derailments of Locomotives on Tangent Track[J]. Vehicle System Dynamics，2013，51(11)：1 784-1 800.

[12] 许自强，吴庆，马卫华，等. 重载机车钩缓装置建模及承压行为[J]. 西南交通大学学报，2014，49(1)：21-26.

XU Ziqiang，WU Qing，MA Weihua，et al. Modeling of Coupler and Draft Gear Systems and Their Compressive Behaviors for Heavy-Haul Locomotives[J]. Journal of Southwest Jiaotong University，2014，49(1)：21-26.

[13] XU Z Q，MA W H，WU Q，et al. Coupler rotation Behaviour and its Effect on Heavy Haul Trains[J]. Vehicle System Dynamics，2013，51(12)：1 818-1 838.

[14] PFEIFFER F，WOLFSTEINER P. Relative Kinematics of Multibody Contacts[C]//Proceedings of the International mechanical Engineering Congress & Exposition.Texas：American Society of Mechanical Engineers，1997：16-21.

[15] GERHARD HIPPMANN. An Algorithm for Compliant Contact Between Complexly Shaped Bodies[J]. Multibody System Dynamics，2004(12)：345-362.

[16] 中国北车集团四方车辆研究所. TB/T 2950—2006 机车车辆车钩连接轮廓[S]. 北京：中国铁道出版社，2006.

[17] 中国南车集团株洲电力机车有限公司. 关于SS4G、HXD1机车钩缓问题及钩缓改进后情况分析报告[R]. 株洲：中国南车集团株洲电力机车有限公司，2008.