铁路货物运输保本距离分析及其粒子群算法

张汉坤， 刘世峰， 宫大庆

(北京交通大学 经济管理学院， 北京 100044)

铁路货物运输保本距离，即铁路货物运输盈亏平衡点，是以运输距离为对象的盈亏平衡点的计算问题，可以描述为在确定货物品类和发送量的前提下，运输距离为多少可以达到盈亏平衡。铁路运输企业受客户委托后，确定需要运输的货物品类和发送量，以及发货车站和到货车站，但是实际的行车路线是由铁路运输企业规划，而选择不同的线路，运行的实际里程和使用的机车将不同，机车走行作业量、牵引作业量以及工务、电务、车辆等部门的作业量也将不同，不同线路单位作业成本也不同，导致运输成本不同，甚至影响到货物运输的盈亏。即由于线路条件、设备运用效率等差异，相同货物在不同地区、不同企业以及使用不同的运输设备、采用不同的组织方式等，运输成本水平将不同[1]。

国内学者主要对铁路货物运输成本进行研究，并应用本量利对铁路运输进行分析。李岱安和徐刚等[2]，根据铁路运输生产特点将运输生产过程划分为发送、中转、运行和到达4个环节，对铁路运输的成本进行核算。李岱安[3]基于此研究以运量和营业收入额为对象的铁路运输企业保本点。刘杰、何世伟和宋瑞等[4]，考虑铁路、航空以及水运固定出发时间对多式联运动态路径选择的影响，将运输费用细化为固定、路段运输、中转以及等待出发等费用。欧美国家研究盈亏平衡距离，主要以铁路公路联合运输为对象，研究联运的盈亏平衡距离[5]，供托运者选择联运或单一公路运输和决策者是否鼓励托运者使用联运作参考[6]。低于盈亏平衡距离单一公路运输有比较优势，而高于盈亏平衡距离联运有比较优势[7-8]。一般认为在中长距离货物运输中铁路比公路更加环保[9]，增加货车的运能可以降低经济和环境成本让联运更高效[10]。在铁路公路联运中货物始发与终到之间的距离必须高于盈亏平衡距离，这是因为联运成本包含从公路到铁路或者铁路到公路的联运端运营商额外收取的费用[11]。公路和联运成本构成变化影响盈亏平衡距离[12]。图1中，当固定成本下降时，曲线向下平移；当变动成本增加时，曲线的斜率变大[12]。例如，联运终端装卸费用和联运两端公路运输成本等增加时，盈亏平衡距离增大[13]。欧洲的研究者认为欧盟委员会(European Commission)建议的300 km联运距离是可行的[14]；北美的研究者通过市场观察评估确定为800 km[6]。

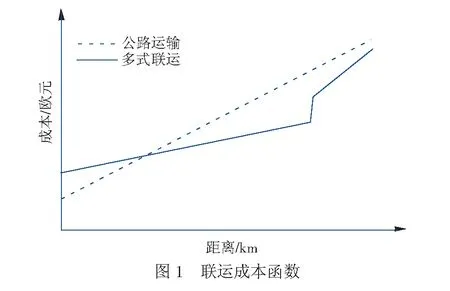
可以发现，现有研究主要集中在铁路运输成本核算和基于运量与营业收入额为对象的保本分析，以及联运保本距离分析，没有单独对铁路货物运输建立以运输距离为对象的本量利分析(cost-volume-profit analysis，CVP)。因此，本文基于传统本量利分析构建运输企业保本距离分析，并结合决定铁路运输成本复杂性的被运送对象与运输工具(移动设备)运动的不完全一致性本质特征[15]，分析铁路货物运输保本距离，为铁路运输企业接收托运和选择运输经由提供参考，优化利用资源，提升铁路运输竞争力，实现利益的最大化。

1 保本距离建模

本量利分析，是企业经营决策过程中重要辅助分析工具，通过全面分析成本、产量和利润之间的相互关系，为企业预测、决策和控制等提供科学依据[16-18]。传统的本量利分析假定，所有成本可划分为固定和变动成本两部分；销售收入与产量、成本与产量之间呈线性关系[16]。固定成本在一定条件下不变，而变动成本与产量成正比例关系[19]。本量利分析基本关系式为

P=RV-(VCV+FC)

( 1 )

式中：P为利润；V为产量；RV为收入；VCV为变动成本；FC为固定成本。

运输服务企业与一般制造企业不同，运输服务企业不生产产品，只是提供运输服务。提供运输服务时，按照托运货物重量和运输距离收取费用。假设运输费用和运输距离成线性关系[20]。因此，运输服务企业本量利分析可表示为

P=RW,L-VCW,L+FCW

( 2 )

式中：W为货物重量；L为运输距离；RW,L为运输收入；VCW,L为变动成本；FCW为固定成本。

本量利分析的核心部分是确定“盈亏平衡点”[21]。作业基础本量利分析的假设也指出，企业以利润最大化为目标，而且盈利突破零(即保本)信息至关重要[22-23]。对于运输服务企业，盈亏平衡点表现为运输距离，即运输距离达到多少时刚好收支相抵，利润为0，超过盈亏平衡点的运输距离将带来利润。因此，运输服务企业的本量利分析盈亏平衡点(即保本点)，也称为保本距离，基本公式为

( 3 )

区别于铁路与其他运输方式的本质特征，由于铁路运输生产活动的网络性而货物流动与运载工具的移动之间的非完全一致性对应，决定铁路运输产品成本的复杂性，整个网络对运输产品生产过程的全局性支持、移动设备对固定化的基础设施的排他性占用和运输产品对资源的联合性消耗[15]。应对3种情况，可将铁路运输成本分为3个部分，即变动成本、半变动成本和固定成本[2,24]。铁路货物运输是铁路运输企业通过机车、车辆以及各类基础设施，在点线面综合协调下实现运送对象的空间位置变化，所以成本特性必然与机车、车辆等设施和设备的运用效率以及管理水平紧密相关[1]。对3部分成本分别产生不同影响，这种影响也反映在距离平衡分析中，即铁路货物运输的成本同时与铁路运输企业的作业效率有关。因此，建立铁路货物运输的本量利分析和保本距离分析模型为

P=RW,L-VCW,E,L+FCW,E

( 4 )

( 5 )

式中：E为作业效率参数；VCW,E,L为变动成本；FCW,E为固定成本。

2 保本距离分析

2.1 运输收入

运输收入指在确定货物品类(即确定对应使用的运价号)和发送量的前提下，铁路运输企业提供货物运输服务而向客户收取的费用。铁路货物运输收入可分为与运输距离和发送重量有关和无关两个部分，因铁路运输企业在提供基本运输服务同时，托运者可以根据实际需要选择两端服务，例如接取或送达货物和仓储货物等，该部分费用主要通过与运输距离和发送重量无关部分体现，即额外收取相关费用。因此，本文根据实际情况和文献[25]及各类货物铁路运输(整车)基准运价率见表1，进一步简化建模分析，仅考虑与运输距离和发送重量有关部分费用收入，即铁路货物运输收入为

RW,L=r1+r2×L×W

( 6 )

式中：r1为基价1；r2为基价2。

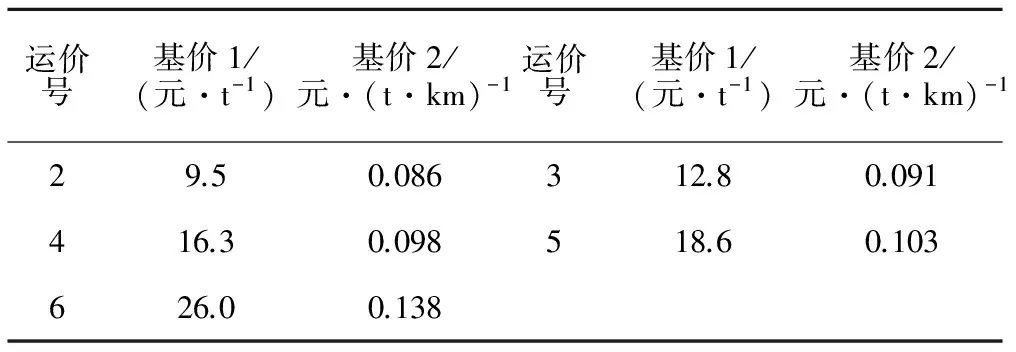
表1 各类货物铁路运输(整车)基准运价率

2.2 运输成本

运输成本，根据铁路货物运输的过程，可以细分为发送、运行、中转、到达和两端服务共5个环节。根据运输收入分析，运输成本只考虑前面4个环节成本。每个环节细化作业量指标，见表2。

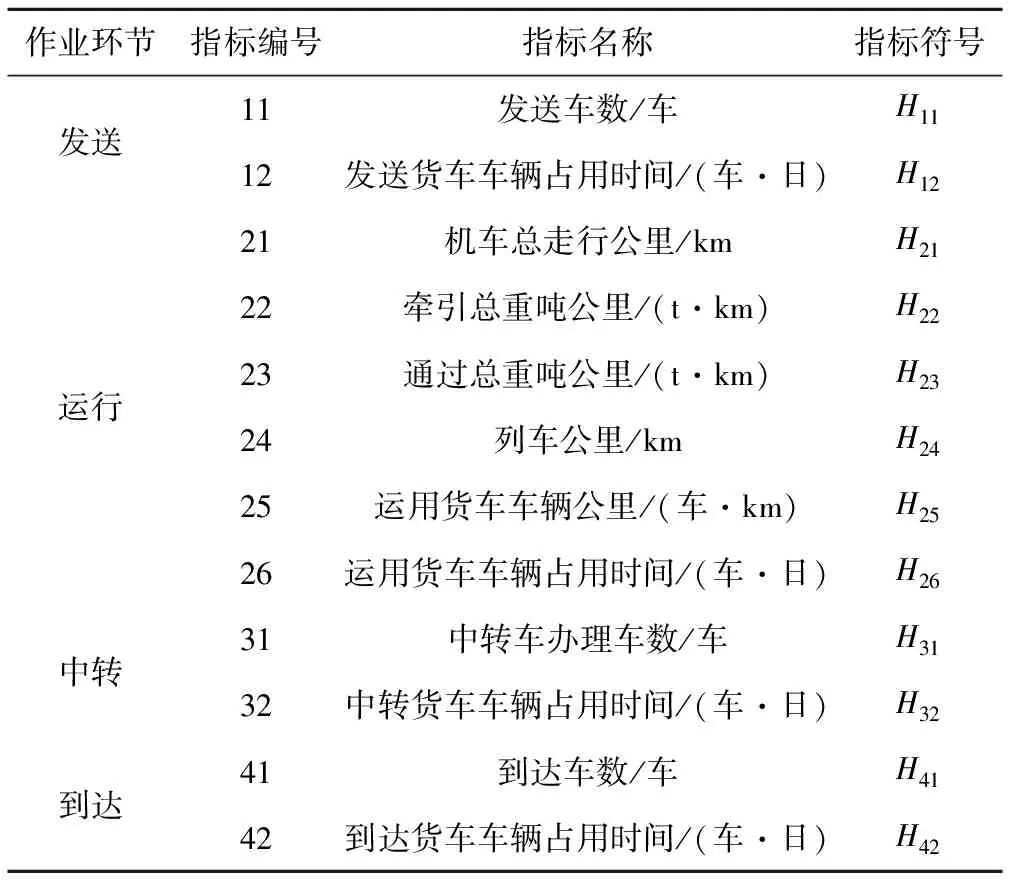
表2 作业量指标

运输成本通过计算作业成本得到，作业成本计算的一般原理是单位作业成本乘以作业量，根据运输服务企业保本距离分析，成本支出按与作业量的变动关系，又可分为固定成本、变动成本[24]，得到

VCW,E,L=

C21×H21+C22×H22+C23×H23+

C24×H24+C25×H25+C26×H26

( 7 )

FCW,E=C11×H11+C12×H12+

C31×H31+C32×H32+

C41×H41+C42×H42

( 8 )

式中：Hij为第i环节第j个作业量指标；Cij为对应Hij的单位作业成本。

2.3 作业量指标计算

作业量指标分为发送、运行、中转和到达4个环节，分别对应车站、机务、供电、工务、电务和车辆等部门的作业。

(1) 发送环节

发送环节对应发送站和车辆部门的作业，发送站作业量为发送车数，车辆部门的作业量为发送货车车辆占用时间。

① 发送环节作业量：发送车数

( 9 )

式中：γ为静载重。

② 发送货车车辆占用时间：货车占用时间

(10)

式中：τ1为作业停留时间；ε为空率。

(2) 运行环节

运行环节分别对应机务、供电、工务、电务和车辆部门的作业。机务部门作业量为机车走行作业量、内燃或电力(供电部门)机车牵引作业量；工务部门作业量为通过总重吨公里；电务部门作业量为列车公里；车辆部门作业量为车辆走行作业量、运行货车车辆占用时间。

① 机车走行作业量：机车总走行公里

1+ζ1+ζ2+ζ3×1+ζ4

(11)

式中：σ为机车平均牵引重量；ω1为车辆自重；ζ1为单机率；ζ2为重联率；ζ3为补机率；ζ4为换算走行率。

② 内燃或电力(供电部门)机车牵引作业量：牵引总重吨公里

(12)

③工务作业量：通过总重吨公里

(13)

式中：ω2为机车自重。

④ 电务作业量：列车公里

(14)

⑤ 车辆作业量：运用货车车辆公里

(15)

⑥运用货车车辆占用时间：货车占用时间

(16)

式中：ν为旅行速度。

(3) 中转环节

中转环节对应中转站和车辆部门的作业，中转站作业量为中转车办理车数和车辆部门的作业量为中转货车车辆占用时间。

① 中转车辆作业量：中转车办理车数

(17)

式中：π为中转次数。

② 中转货车车辆占用时间：货车占用时间

(18)

式中：τ2为中转平均停留时间。

(4) 到达环节

到达环节对应到达站和车辆部门的作业，到达站作业量为到达车数和车辆部门的作业量为到达货车车辆占用时间。到达环节的作业量，在数值上与发送的作业量相等。

① 到达环节作业量：到达车数

(19)

② 到达货车车辆占用时间：货车占用时间

(20)

3 保本距离求解

3.1 模型求解

由铁路货物运输本量利分析模型可得

r1+r2×L×W=C11×H11+C12×H12+

(C21×H21+C22×H22+C23×H23+

C24×H24+C25×H25+C26×H26)+

(C31×H31+C32×H32)+

(C41×H41+C42×H42)

(21)

代入相应作业量指标，整理后得到

(r1+r2×L)×W=

1+ζ1+ζ2+ζ3×1+ζ4+

(22)

求解得到铁路货物运输保本距离分析模型

L=

(23)

设

(24)

(25)

式中：r3为发送站发送每吨货物的作业成本；r4为运输每吨货物每公里的作业成本。铁路货物运输保本距离分析模型为

(26)

3.2 目标函数

由保本距离计算模型可得，保本距离存在的基本条件是分母不为0，即当下式成立时，保本距离不存在

r2=r4

(27)

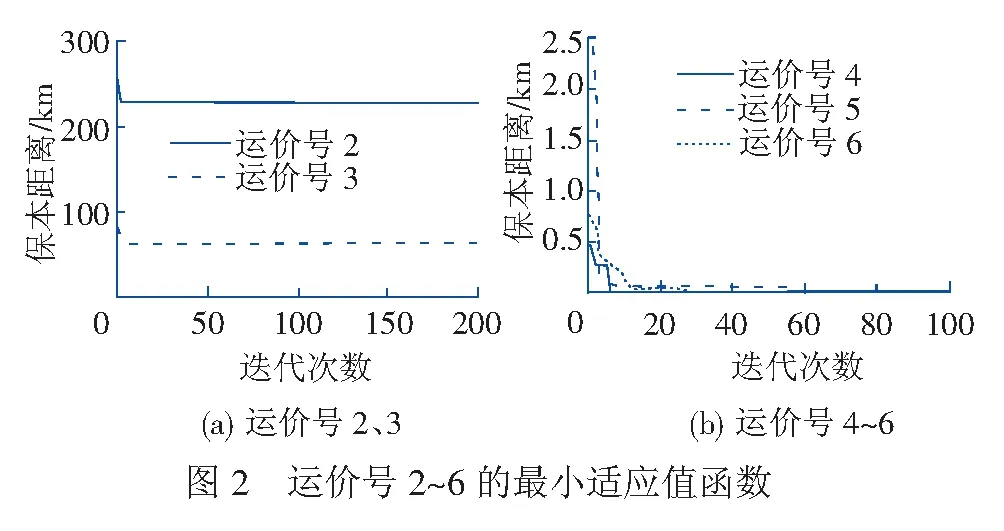
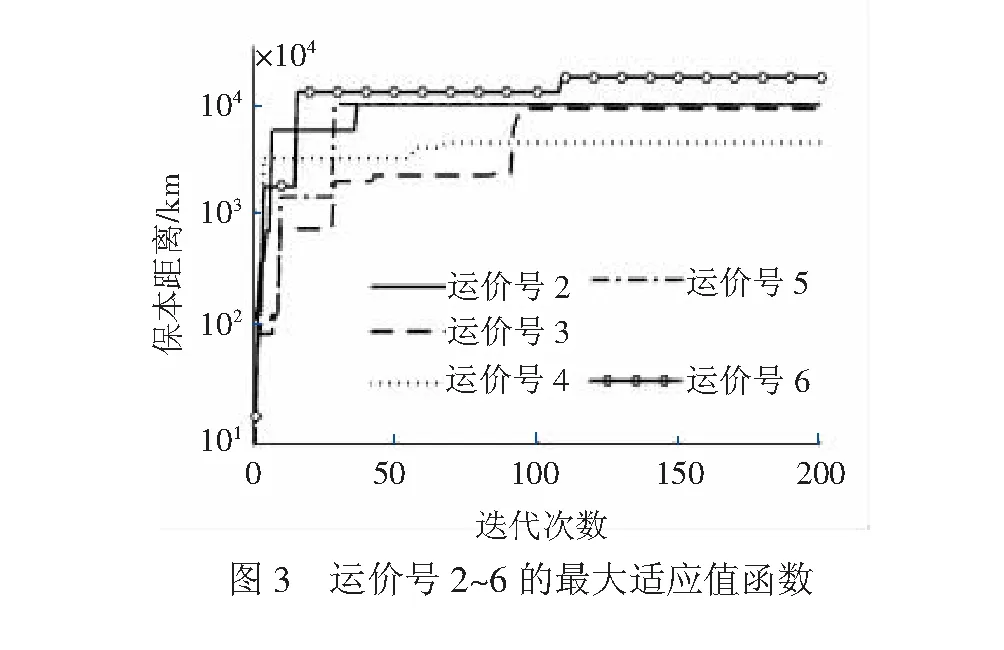
此时，铁路运输企业的货物运输盈亏与距离无关，如果r1=r3，则货物运输盈亏平衡，即任何距离均是保本点；如果r1>r3，则货物运输均盈利；如果r1r4，则货物运输均盈利；如果r2

但是，保本距离存在不一定有意义，且不一定有实际意义。当满足以下条件时，保本点存在但为负数，没有意义。

r1r3∩r2>r4

(28)

此时，如果r1>r3∩r2>r4，货物运输运输任何距离均盈利；r1

为得到有意义的结果，还需进一步满足相应的条件。保本距离有意义，是指满足计算模型分母不为0的基本条件，同时满足保本距离的计算结果不能是负数，即要大于0。按照保本距离计算模型，分子和分母都是由2个相减的部分组成。所以，要保证结果能够大于0，也就是为正数，即需要保证分子和分母的计算结果有相同的符号。即满足以下条件

r1r4∪r1>r3∩r2

(29)

此时，如果r1r4，保本距离L的含义为货物运输运输距离大于L则能实现盈利，小于L则亏损，根据保本距离分析可知，此时L有实际意义；如果r1>r3∩r2

根据以上分析，在作业效率范围内调整作业效率指标，使保本距离有实际意义，即r1r4，在此作业效率水平下运输距离大于此时L，或在此运输L距离条件下进一步提高作业效率(提高资源利用效率)，可以实现企业最终盈利的目的。由于技术经济特征的制约，设备等运用效率的提高要受到一定的限制[1]，根据文献[26]统计数据设定作业效率见表3。即在作业效率范围内调整作业效率指标，保本距离可能存在极值：如果最小Lmin存在，则小于Lmin距离货物运输铁路运输企业均不能受理，此时运输一定亏损；如果最大Lmax存在，则大于Lmax距离货物运输铁路运输企业均可以受理，此时运输盈利。

表3 作业效率表

注：约束条件“dp=-1”表示保留1位小数；“dp=-2”表示保留2位小数。

基于以上分析，构建铁路货物运输保本距离分析的目标函数。

4 基于MPPSO算法算例验证

4.1 算法设计

粒子群算法(Particle Swarm Optimization,PSO)是Kennedy和Eberhart受Heppner和Grenander的相关工作和鸟群觅食行为启发提出的，很快发展成为有效的优化方法[27-28]。PSO的优化速度和性能有很大提高，而且具有很好的鲁棒性，在全局优化领域应用广泛[29]。大多数随机算法(包括PSO)和遗传算法都受制于“维数灾难”问题，即随着搜索空间维数的增加性能下降[30]。为增加PSO算法种群多样性和问题的空间探索能力，把粒子群分成多组并引入多相和Davis爬山算法的思想，提出MPPSO[31-34]。MPPSO算法有助于扩大问题空间的探索能力，增加种群的多样性，并且防止过早收敛[33]。通过实验证明，MPPSO算法的寻优能力和鲁棒性优于PSO[35-36]。PSO算法应用在铁路集装箱中心站轨道门吊调度优化和全路空车动态调配问题中，解决其优化问题[37-38]；Qi、Ruan和Shi等[35]将MPPSO算法应用于逆辐射问题研究中，得到优于PSO的其它算法结果。从上面分析可知，铁路货物运输保本距离分析是复杂的问题。因此，本文采用MPPSO求解问题。

MPPSO算法通过位置更新公式改变他在群中的位置，速度和位置更新式为

vidt+1=Cvvidt+Cxxidt+Cggdt

(30)

xidt+1=xidt+vidt+1

(31)

式中：Cv、Cx、Cg为每个相位内每个组的系数值；gd(t)为t时刻所有粒子目前为止经历过的最好位置d维分量；vidt、vidt+1分别为t和t+1时刻粒子i速度d维分量；xidt、xidt+1分别为t和t+1时刻粒子i位置d维分量。

MPPSO算法首先给出相位数目ph，相位变化频率pcf，每个相位的群的数目g和速度变化变量VC，并初始化粒子速度和位置以及全局最优位置，然后开始迭代直到满足终止条件为止。本文在MPPSO算法基础上，对每个维度进行sl子长度更新，在Rastrigin函数实验中，问题的维数D=30，其他参数同下，算法独立运行30次，得到最优值 2.110 9e-13±4.006 49e-13，算法性能(收敛速度和最优值)得到显著提高。因此，MPPSO算法的伪代码(matlab)为

%% Step0 确定以下参数T、D、N、ph、pcf、g、VC

%% Step1 初始化粒子群粒子的速度v和位置x，以及粒子群全局最优位置Pgx及最优值Pg

%% Step2 迭代

fort=1:T

%判断是否满足重新初始化速度条件，如果满足条件则重新初始化速度

%确定当前的相位

%处理每个粒子

fori=1:N

%确定当前的粒子分组

%确定维数的子长度

sl=roundnrand×min10,D-1+1,0;

%对粒子的每个维度进行处理

ford=1:D

%缓存粒子初始位置

temp1,:=xi,:;

%处理粒子每个子维度

forj=0:sl

%更新维数

d_temp=d+j;

%判断是否超出维数，超出维数则推导出循环

%确定速度更新公式的系数值

%根据式(30)更新速度

vi,d_temp=Cv×vi,d_temp+

Cx×xi,d_temp+Cg×Pgxd_temp;

%根据式(31)更新位置缓存

temp1,d_temp=xi,d_temp+

vi,d_temp;

end

%判断新临时位置是否改进适应度，是则接受临时更新

iffitnesstemp

%接受临时更新

xi,:=temp1,:;

end

end

end

% 更新粒子群全局最优位置

fori=1:N

% 计算适应度

f=fitnessxi,:;

iff

Pgx=xi,:;

Pg=f;

end

end

end

4.2 算例分析

单位作业成本与作业量指标相对应，指每完成1个单位的作业所消耗的资源(成本)，用于计算各项作业的成本。根据某铁路货物运输企业13年实际的单位作业成本编制的单位作业成本[39]，见表4。

表4 作业量指标的单位作业成本

根据文献[32,34]，MPPSO算法相关参数设置：ph=2、pcf=5、g=2、sl∈1,min10,D、VC=10、Cv=rand( )，当相位1子种群1或相位2子种群2时，Cx=rand( )、Cg=-rand( )；当相位1子种群2或相位2子种群1时、Cx=-rand( )、Cg=rand( )。根据实验效果，实际情况和参考规范PSO参数设置其他参数：最大迭代次数T=200、问题的维数D=14、粒子群个体数目N=30。通过MPPSO算法求解，在根据实际情况精确到整数，独立运行30次，各运价号最小、最大保本距离见表5。某次运行过程中，最小适应值函数见图2(a)、图2(b)，最大适应值函数见图3。

表5 各运价号最小、最大保本距离

注：根据铁路运输实际情况，保本距离大于1万km，则认为最大保本距离不存在，表示为“—”。

由表5可知，在表4作业成本和表3作业效率情况下:

(1) 如果根据客户托运货物确定收费使用运价号为2，则托运距离不能小于227 km，否则运输将亏损；

(2) 如果根据客户托运货物确定收费使用运价号为3，则托运距离不能小于60 km，否则运输将亏损；

(3) 运价号2、3的最小保本距离对应的作业参数取值，见表6，在运价号2、3对应货物运输中，作业参数静载重、机车平均牵引重量和旅行速度变大而其他作业参数变小，可以使保本距离变小；

(4) 如果根据客户托运货物确定收费使用运价号为4～6，则通过调整作业参数使保本距离存在，即通过调整作业参数可以实现盈利；

(5) 所有运价号的最大保本距离均不存在(大于1万km，根据实际情况则认为不存在)，即在目前基准运价率下，绝对盈利保本距离不存在。

表6 运价号2、3的最小保本距离对应的作业参数取值

5 结论

本文从传统的本量利分析出发，结合运输服务企业的特点，构建运输服务企业的本量利和保本距离分析模型。由于货物流动与运载工具的移动之间的非完全一致性对应，决定铁路运输成本的复杂性，与铁路运输企业的作业效率有关，是区别于其他运输方式的本质特征。根据铁路货物运输成本的特殊性，构建铁路货物运输本量利和保本距离分析模型。

结合铁路货物运输实际情况，求解保本距离分析模型，由于技术经济特征的制约，铁路运输企业的作业参数调整受到一定的限制，在保本距离具有实际意义基础上对模型进行分析，结合现有作业成本和作业效率，构建铁路货物运输保本距离分析目标函数。

本文利用MPPSO算法对铁路货物运输保本距离进行求解，得到目标函数值——各运价号在给定的作业成本和作业效率下对应的最小、最大保本距离，为铁路运输企业接收托运和运输经由选择等提供参考。在表4作业成本和表3作业效率下，运价号2和3最小保本距离分别为227 km和60 km，分别小于该距离的运价号2和3对应的货物运输，铁路运输企业均不能受理；在其他条件下，各运价号对应货物运输均不存在绝对盈利运输距离。

在表4作业成本和表3作业效率情况下，运价号2、3的最小保本距离对应的作业参数取值可以看出，保本距离有实际意义的情况下，作业参数静载重、机车平均牵引重量和旅行速度变大而其他10个作业参数变小，保本距离变小。即作业参数静载重、机车平均牵引重量和旅行速度变大而其他10个作业参数变小，可以降低铁路货物运输成本。

实际工作中，不同机型的机车总走行公里，不同车种的运用货车车辆公里和占用时间，以及不同线路等级的通过总重吨公里和列车公里，对应单位作业成本不一样；牵引总重吨公里对应单位作业成本，依据实时能源单价(电价和油价)和机车单耗决定。本文为简化分析过程，分别采用平均单位作业成本代替机种、车种和线路等级对应单位作业成本，这将是今后研究的重点。

参考文献：

[1] 徐刚. 铁路货物运输成本特性研究[J]. 铁道学报, 2002, 24(6): 11-14.

XU Gang. Research on Cost Feature of Railway Freight Traffic[J]. Journal of the China Railway Society, 2002, 24(6): 11-14.

[2] 李岱安, 徐刚. 中国铁路运输成本计算系统的研究[J]. 铁道学报, 1999, 21(6): 96-100.

LI Daian, XU Gang. Study on China Railroad Costing System (CRCS)[J]. Journal of the China Railway Society, 1999, 21(6): 96-100.

[3] 李岱安. 中国铁路成本计算[M]. 北京: 中国铁道出版社, 1999: 182-194.

[4] 刘杰, 何世伟, 宋瑞, 等. 基于运输方式备选集的多式联运动态路径优化研究[J]. 铁道学报, 2011, 33(10): 1-6.

LIU Jie, HE Shiwei, SONG Rui, et al. Study on Optimization of Dynamic Paths of Intermodal Transportation Network Based on Alternative Set of Transport Modes[J]. Journal of the China Railway Society, 2011, 33(10): 1-6.

[5] RUTTEN B J C M. On Medium Distance Intermodal Rail Transport: A Design Method for a Road and Rail Inland Terminal Network and the Dutch Situation of Strong Inland Shipping and Road Transport Modes[D]. Delft: Delft University of Technology, 1995: 51-57.

[6] KIM N S, VAN WEE B. The Relative Importance of Factors that Influence the Break-even Distance of Intermodal Freight Transport Systems[J]. Journal of Transport Geography, 2011, 19(4): 859-875.

[7] JANIC M. Modelling the Full Costs of an Intermodal and Road Freight Transport Network[J]. Transportation Research Part D: Transport and Environment, 2007, 12(1): 33-44.

[8] MACHARIS C, VAN HOECK E, PEKIN E, et al. A Decision Analysis Framework for Intermodal Transport: Comparing Fuel Price Increases and the Internalization of External Costs[J]. Transportation Research Part A: Policy and Practice, 2010, 44(7): 550-561.

[9] JANIC M, VLEUGEL J. Estimating Potential Reductions in Externalities from Rail-road Substitution in Trans-european Freight Transport Corridors[J]. Transportation Research Part D: Transport and Environment, 2012, 17(2): 154-160.

[10] YE Y, SHEN J, BERGQVIST R. High-capacity Transport Associated with Pre- and Post-haulage in Intermodal Road-rail Transport[J]. Journal of Transportation Technologies, 2014, 4(3): 289-301.

[11] BIERWIRTH C, KIRSCHSTEIN T, MEISEL F. On Transport Service Selection in Intermodal Rail/Road Distribution Networks[J].Business Research, 2012,5(2): 198-219.

[12] MACHARIS C, VANHAVERBEKE L, VAN LIER T, et al. Bringing Intermodal Transport to the Potential Customers: An Interactive Modal Shift Website Tool[J]. Research in Transportation Business & Management, 2012, 5: 67-77.

[13] HANSSEN T E S, MATHISEN T A, JORGENSEN F. Generalized Transport Costs in Intermodal Freight Transport[J]. Procedia-social and Behavioral Sciences, 2012,54: 189-200.

[14] MEERS D, VERMEIREN T, MACHARIS C,et al.Sustainable Logistics[M]. Bradford: Emerald Group Publishing Limited, 2014: 217-243.

[15] 毕守锋, 徐刚. 铁路成本代理模型研究[J]. 技术经济, 2006, 25(12): 35-37.

BI Shoufeng, XU Gang. Research on the Railways Cost Proxy Models[J]. Technology Economics, 2006, 25 (12): 35-37.

[16] 王福胜, 李汉铃, 章轶. 基于作业成本法的本量利用分析方法研究[J]. 中国软科学, 2002(8): 118-121.

WANG Fusheng, LI Hanling, ZHANG Yi. Cost-volume-profit Analysis Method Based on Activity-based Costing[J]. China Soft Science, 2002(8): 118-121.

[17] 邓为民, 司书宾. 约束条件下多产品作业基础CVP分析模型[J]. 计算机集成制造系统, 2003, 9(3): 231-236.

DENG Weimin, SI Shubin, SUN Shudong. Cost-volume-profit Analysis Model with Constraints Based on Multi-product Activity[J]. Computer Integrated Manufacturing Systems, 2003, 9(3): 231-236.

[18] 洪慧, 韩海涛, 王智琦. 高校数字图书馆本量利模型构建及实证研究[J]. 情报杂志, 2009, 28(6): 35-38.

HONG Hui, HAN Haitao, WANG Zhiqi. Cost-volume-profit Model Construction and Empirical Research of University Digital Library[J]. Journal of Information, 2009, 28(6): 35-38.

[19] 梁伦腾. 盈亏平衡分析法在企业生产经营决策中的应用[J]. 经济与管理研究, 2000(1): 77-78.

LIANG Lunteng. Application of Break-even Analysis in Enterprise Production and Management Decision-making[J]. Research on Economics and Management, 2000(1):77-78.

[20] 张运河, 林柏梁, 梁栋, 等. 优化多式联运问题的一种广义最短路方法研究[J]. 铁道学报, 2006, 28(4): 22-26.

ZHANG Yunhe, LIN Boliang, LIANG Dong, et al. Research on a Generalized Shortest Path Method of Optimizing Intermodal Transportation Problems[J]. Journal of the China Railway Society, 2006, 28(4): 22-26.

[21] 明黎. 本量利分析法在银行盈亏平衡分析中的应用[J]. 经济与管理研究, 2006(2): 61-64.

MING Li. Application of CVP Analysis in the Bank Break-even Analysis[J]. Research on Economics and Management, 2006(2): 61-64.

[22] 汪方军, 万威武, 王平心. 基于作业的本量利模型及保本分析[J]. 系统工程理论与实践, 2002, 22(3): 32-39.

WANG Fangjun, WAN Weiwu, WANG Pingxin. Activity-based CVP Model and BEP Analysis[J]. Systems Engineering-theory & Practice, 2002, 22(3): 32-39.

[23] 王平心, 汪方军, 杨敏. 以作业为基础的本量利分析[J]. 数量经济技术经济研究, 2001(10): 121-124.

WANG Pingxin, WANG Fangjun, YANG Min. Activity-based CVP Analysis[J]. The Journal of Quantitative & Technical Economics, 2001(10): 121-124.

[24] 李岱安, 范秀君. 中国铁路成本计算系统[J]. 中国铁路, 2001(10): 7-11.

LI Daian, FAN Xiujun. Costing System of Chinese Railways[J]. Chinese Railways, 2001(10): 7-11.

[25] 国家发展改革委. 国家发展改革委关于调整铁路货运价格进一步完善价格形成机制的通知[EB/OL]. http://jgs.ndrc.gov.cn/zcfg/201501/t20150130_662799.html, 2015-01-29.

[26] 中国铁路总公司档案史志中心. 中国铁道年鉴(2013)[M]. 北京: 中国铁道出版社, 2014: 485-486.

[27] POLI R, KENNEDY J, BLACKWELL T. Particle Swarm Optimization[J]. Swarm Intelligence, 2007, 1(1): 33-57.

[28] BANKS A, VINCENT J, ANYAKOHA C. A Review of Particle Swarm Optimization Part I: Background and Development[J]. Natural Computing, 2007, 6(4): 467-484.

[29] SONG M P, GU G C. Research on Particle Swarm Optimization: A Review[C]//Proceedings of the Third International Conference on Machine Learning and Cybernetics. Shanghai: IEEE, 2004:2 236-2 241.

[30] VAN DEN BERGH F, ENGELBRECHT A P. A Cooperative Approach to Particle Swarm Optimization[J]. Evolutionary Computation, IEEE Transactions on, 2004, 8(3): 225-239.

[31] AL-KAZEMI B S N, MOHAN C K. Multi-phase Discrete Particle Swarm Optimization[C]//Proceedings of fourth international workshop on frontiers in evolutionary algorithms (FEA 2002), 2002.

[32] AL-KAZEMI B, Mohan C K. Multi-phase Generalization of the Particle Swarm Optimization Algorithm[C]//Proceedings of the 2002 Congress on Evolutionary Computation. Hawaii:IEEE,2002:489-494.

[33] AL-KAZEMI B, MOHAN C K. Training Feed Forward Neural Networks Using Multi-Phase Particle Swarm Optimization[C]//Proceedings of the 9th International Conference on Neural Information Processing. Singapore:IEEE, 2002:2 615-2 619.

[34] AL-KAZEMI B S N M. Multiphase Particle Swarm Optimization[D]. New York: Syracuse University, 2002: 23-34.

[35] QI H, RUAN L M, SHI M, et al. Application of Multi-phase Particle Swarm Optimization Technique to Inverse Radiation Problem[J]. Journal of Quantitative Spectroscopy and Radiative Transfer, 2008, 109(3): 476-493.

[36] QI H, RUAN L, WANG S, et al. Application of Multi-phase Particle Swarm Optimization Technique to Retrieve the Particle Size Distribution[J]. Chinese Optics Letters, 2008, 6(5): 346-349.

[37] 王力, 朱晓宁, 闫伟, 等. 铁路集装箱中心站轨道门吊调度优化模型与算法[J]. 铁道学报, 2014, 36(5): 8-13.

WANG Li, ZHU Xiaoning, YAN Wei, et al. Optimization Model and Algorithm of Rail Mounted Gantry Crane Scheduling at Railway Container Terminals[J]. Journal of the China Railway Society, 2014, 36(5): 8-13.

[38] 王龙, 马建军, 林柏梁, 等. 全路空车动态调配及路网分界口排空流量测算方法[J]. 铁道学报, 2015, 37(6): 1-9.

WANG Long, MA Jianjun, LIN Boliang, et al. Dynamic Empty Car Distribution for the Whole Rail System and Calculation for Empty Car Flow Discharged over Network Boundaries[J]. Journal of the China Railway Society, 2015, 37(6): 1-9.

[39] 徐刚, 郭雪萌. 铁路运输成本管理研究[R]. 北京: 中国铁路经济规划研究院,北京交通大学,2014:108-116.