计及接触网空气动力的高速弓网动态受流特性研究

宋 洋， 刘志刚， 鲁小兵， 汪宏睿， 张 静

(西南交通大学 电气工程学院， 四川 成都 610031)

受电弓-接触网系统为高速运行的列车输送电能，随着列车运行速度的提高，弓网之间的动态性能成为制约列车高速运行的关键因素之一[1]。接触网沿线露天架设，其工作环境十分恶劣，外部环境对其影响十分复杂。其中最常见的是环境风载荷，接触网在风场中的振动直接影响弓网间的接触特性，从而影响弓网间的受流质量，因此，在研究弓网动态行为时，考虑风载荷的影响是很有必要的。

目前弓网系统动力学的研究在国内外已引起了广泛的重视，弓网动力学模型的建立与修正日趋成熟，如文献[2-6]等。对弓网空气动力学的研究一方面集中在对受电弓在高速气流下减阻抗噪的研究，如文献[7-8]。另一方面，对接触网风振的研究也引起了众多学者的关注，文献[9]利用谐波合成法和脉动风功谱模拟了水平脉动风速，用于研究强风地区接触网的屈曲和接触网疲劳可靠性问题；文献[10]推导了接触网的抖振力模型，并对其抖振时程进行分析；文献[11-12]对在随机风场中弓网动态性能进行仿真研究，认为随机风场是研究弓网受流不可忽略的因素；文献[13]基于AR模型，采用线性滤波法模拟脉动风场，分析接触网的风振响应，强调了构建风场时考虑时间相关性的重要性。在此基础上文献[14]研究了横风对弓网受流特性的影响；文献[15-16]同时在受电弓和接触网上加风，研究了横风作用下空气动力对弓网动态性能的影响，指出在考虑受电弓强气流扰动的同时，也应考虑环境风对接触网的影响。文献[17]采用Davenport谱和Panosfsk谱，运用谐波合成法分别模拟水平和竖直方向上的脉动风时程，研究了脉动风对高速弓网受流的影响，得出风攻角和风速都是弓网受流影响因素的结论；文献[18]也采用这种方法研究了覆冰接触线的风振响应，得出了覆冰会改变接触网振动形式的结论；文献[19-20]考虑接触网线索的几何非线性，对现有模型进行修正，研究了接触网几何非线性对风偏计算的影响。

但是，这些文献在研究环境风载荷对弓网系统的影响时，存在以下问题：(1)通常将风载荷作为外部激励施加到接触网上，忽略了线索振动与外部流场的耦合关系；(2)未研究接触网线索的气动特性，较少考虑风攻角变化引起的接触网线索气动特性的改变；(3)大多是有限元软件的应用，未从本质上对弓网动力学方程进行空气动力项的修正；(4)较多采用谐波合成法模拟脉动风场，不能考虑脉动风的时间相关性；(5)未能够揭示环境风载荷对弓网受流性能的影响规律。

作用在接触网上的环境风载荷可分为平均风载荷和脉动风载荷，文献[21]指出，作用在接触网线索上的平均风载荷对其振动的影响表现为阻尼性质；而文献[17]指出，作用在接触网线索上脉动风载荷会造成接触网的强振动响应，称为抖振。前者是接触线、承力索的位移与外界流体耦合造成的流致振动，后者是外界激励造成的强迫振动。本文为研究这2种形式的空气动力对弓网受流特性的影响，分别推导了作用在接触线、承力索上的空气阻尼和竖直方向上的脉动风载荷，基于模态分析法修正传统弓网动力学方程，采用流体力学计算方法研究接触线的气动特性，通过求解分别研究环境风表现出的2种空气动力特性对弓网受流的影响，并揭示脉动风作用下风速和风攻角对接触压力的影响规律。

1 计及空气阻尼的弓网动力学方程推导

当平均风吹过接触网线索时，对接触线、承力索竖向振动的影响表现出的是空气阻尼效应。本节为研究这种效应对弓网受流的影响，首先根据文献[21]的描述推导作用在接触线、承力索上的空气阻尼，然后将其添加到弓网动力学方程中进行修正。

1.1 接触线、承力索上的空气阻尼

接触线、承力索在静风载荷作用下受定长气动力作用，空气阻尼产生的原因在于其上下的微幅振动引起攻角的微小变化。图1为接触线截面迎风受力示意图。

假设空气均匀流以攻角α、速度Uα流过，ρair为气流密度。在风轴坐标系(由FL和FD组成)下，阻力FD(α)和升力FL(α)分别为[22]

( 1 )

式中:CD(α)、CL(α)分别为攻角α时的阻力和升力系数。它们在垂直方向的作用力为

Fy=FD(α)sinα+FLαcosα

( 2 )

为方便起见，可将Fy改写为

( 3 )

式中：Ue是Uα的水平分量,Ue=Uαcosα， 于是

( 4 )

与式( 3 )比较后，可以得到

CFy=(CL+CDtanα)secα

( 5 )

( 6 )

将Fy在α=0处关于α进行一阶泰勒展开

( 7 )

式中：Fy(0)是不随时间变化的，在动态响应分析中可以忽略。Δ(α2)表示高阶项，也可忽略。因此有

( 8 )

由式( 2 )、式( 3 )可知

( 9 )

将式( 9 )代入式( 8 )，可得到定常气动力的表达式

(10)

因此，在横风作用下，接触线、承力索上的空气阻尼可表示为

(11)

1.2 计及空气阻尼的弓网动力学方程

为考虑接触线、承力索的弯曲刚度，常将它们看作是欧拉-伯努利梁单元，常用的接触网力学方程建模方法主要有限单元法[2-3]和模态叠加法[4-6]2种，模态分析法具有求解速度快、节省内存等优点，在研究弓网关系时使用较为广泛，本节亦采用这种方法考虑空气阻尼修正弓网动力学方程。图2为接触网结构的受力图，接触线或承力索的运动偏微分方程为[23]

(12)

式中：EI为接触线、承力索抗弯刚度；T为张力；ρ为线密度；C为系统自阻尼；Fc(x,t)为受电弓抬升力(承力索此项为零)；Fh(x,t)为悬挂装置的作用力。由上文可知

(13)

将其代入式(12)得

(14)

由式(12)可以看出静风载荷对接触网系统的贡献相当于改变了梁单元的阻尼系数。利用分离变量法对式(11)求解，可得到承力索、接触线的振动微分方程分别为

(15)

(16)

式中:qan(t)和qan(t)为由

分解出的广义位移；L为锚段长度；Fa1(xr,t)和Fa2(xr,t)分别为吊弦和支撑杆对承力索的贡献力；Fb1(xr,t)和Fb2(xr,t)为吊弦和定位器对接触线的贡献力；p为吊弦个数；q为定位器和支撑杆个数；ωan和ωbn分别为承力索和接触线的自振角频率。它们分别表示为

(17)

(18)

(19)

(20)

(21)

(22)

其中，MD和KD分别为定位器质量和刚度；MA和KA分别为支撑杆的质量和刚度；MB为定位器质量。

对于受电弓模型，本文采用较为通用的三元受电弓模型，其运动微分方程为

(23)

式中：M1、M2、M3分别是受电弓弓头、上框架、下框架归算质量；C1、C2、C3分别是受电弓弓头、上框架、下框架归算阻尼系数；K1、K2、K3分别是弓头与上框架之间、上下框架之间、下框架与底座之间的等效弹簧刚度；F0为升弓力。

接触压力Fc(xc,t)可采用罚函数法定义

(24)

联立式(15)、式(16)和式(23)、式(24)即可得到弓网耦合动力学方程

(25)

2 接触线、承力索截面的CFD绕流仿真

文献[18]和文献[24]采用CFD方法计算了接触线的气动参数，并与风洞试验对比，证明了采用流体力学数值仿真的方法测量接触线气动参数的可行性。本节也采用这种方法计算不同风速、攻角下的接触线气动参数CL和CD。此方法在研究输电导线风振中已较为常用[25]。本文采用接触线截面为标准的京津城际铁路接触线；承力索截面等效为圆形。图3所示为接触线的截面图及网格划分。

流体采用较为通用的k-epsilion模型，迎风格式采用精度较高的二阶迎风格式。由于承力索截面可看作是规则的圆形截面，其气动力系数不随攻角变化，只与风速有关；而接触线截面是不规则的，为了能够较为全面地考虑接触线截面的特殊性，本次实验每5°取一个攻角，分别仿真了不同风速下攻角在-90°～90°范围内的气动力系数，仿真时具体参数选取可参考文献[18]。表1列出了承力索在不同风速下的气动力系数；图4绘制了不同风速下接触线的气动力系数随攻角变化的曲线。从CL和CD曲线可以看出接触线由于其截面的特殊性，所表现出的气动特性与标准圆柱是完全不同的。将本节仿真出的气动参数代入式(11)即可求得接触线和承力索的空气阻尼。

表1 承力索截面气动力系数

3 空气阻尼对弓网受流特性的影响

接触网参数以京津城际为例，参数见表2；受电弓选取DSA380参数[26]，见表3。车速v取350 m/s，接触刚度KS为82 300，静抬升力与气动抬升力F0=0.000 97×(3.6×v)2+70 N。仿真锚段L取12个跨距，去掉第一跨与后两跨不稳定的数据，取第2到10跨接触压力为研究对象。根据前两节的推导和计算，将不同风速下的空气阻尼带入弓网动力学方程(25)中，并利用Newmark法进行求解，可计算得出考虑不同风速引起的空气阻尼的弓网间接触压力。图5和表4分别为无风时和风速为5、10、20、30 m/s时弓网间的接触压力曲线及其统计量。

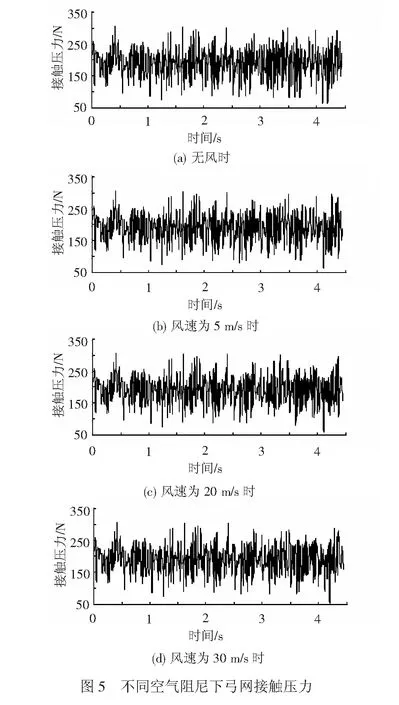
从图5和表4中可以看出，在静风载荷作用下，接触线和承力索的空气阻尼很少，当风速达到30 m/s时承力索阻尼仅有0.213 3，而接触线的也只有0.091 9，且都为正阻尼，不会使接触网形成大幅的自激振动；接触压力的各项统计指标均无明显变化，在正阻尼的作用下，接触线振动还会得到抑制，使得标准差减小，即平均风引起的垂向空气阻尼不会导致弓网受流明显的恶化。但是在这里还要注意2个问题，第一，若在极端气象条件下，尤其是接触线、承力索覆冰，改变了它们的气动力系数，可能会出现较大的负阻尼，在平均风下可能会产生大幅的自激振动，俗称舞动，会对弓网受流造成极大危害，因此，对极端气象条件下的接触网线索空气阻尼进行进一步研究是很有意义的；第二，本文主要关心的是平均风引起的空气阻尼对弓网接触性能的影响，接触网横向偏移导致的刮弓事故不在讨论范围之内。

表2 京津高速铁路接触网主要参数

表3 DSA380归算参数

表4 不同空气阻尼下弓网接触压力统计量

4 计及脉动风激励的弓网动力学方程推导

由前文的推导及仿真结果可知，静风引起的空气阻尼对弓网受流的影响微乎其微，本节将推导计及脉动风激励的弓网动力学方程，研究脉动风激励对弓网受流的影响。

4.1 接触线、承力索上的脉动风激励

作用在承力索/接触线上的脉动风载荷是顺向脉动风和垂向脉动风以及静风载荷叠加而成的，并受风攻角变化的影响[17-18]。

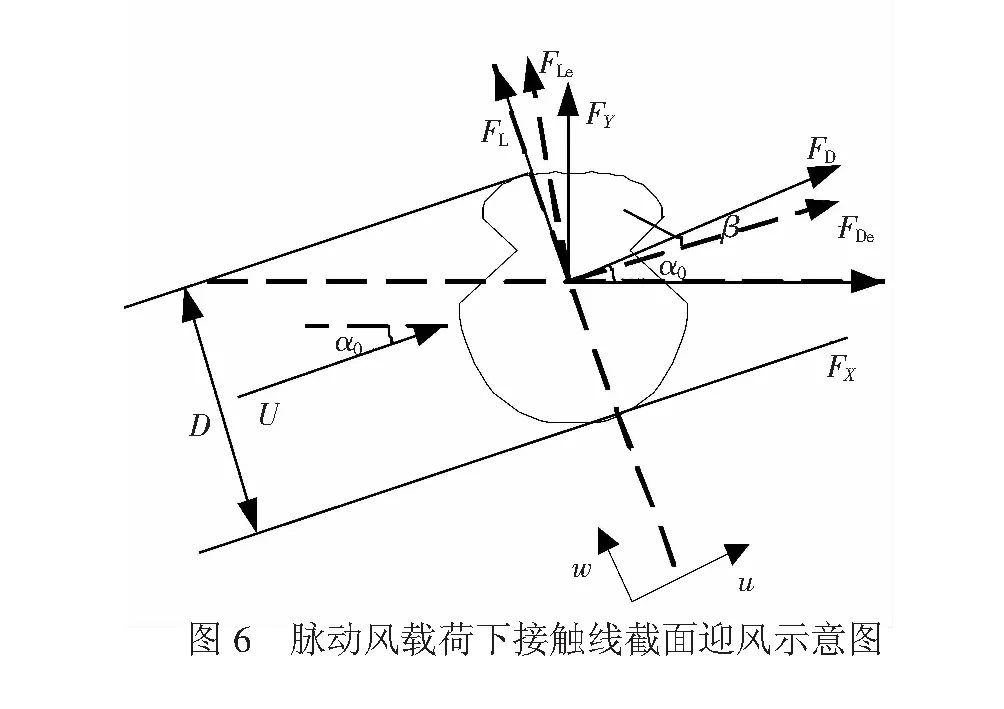
与平均风载荷相似，图6为随机风场作用下接触线截面受力示意图，平均风速为U，初始风攻角为α0，动态迎风角为β，则有效风攻角αe为

(26)

式中:u为顺向脉动风速;w为垂向脉动风速;vx和vy分别为接触线节点顺风向和垂直于风向上的速度。

与推导空气阻尼相似，在相对风轴坐标系中，接触线所受到的气动升力FL和气动阻力FD可以表示为[22]

(27)

(28)

Ur为相对风速，可由下式计算

(29)

由于动态迎风角β很小，则气动载荷的水平分量FDe和竖直分量FLe可以表示为

(30)

将式(27)代入式(30)中，并忽略高阶项可得到

(31)

(32)

将其变换到体轴坐标系，可得到影响受流的垂向脉动风载荷

Fgy=FDesinα0+FLecosα0

(33)

4.2 接触线、承力索上的脉动风激励

根据1.2节的推导思路，令作用在梁单元上的竖直方向上的气动力Fy=Fgy，则式( 2 )可以写成如下形式

(34)

由于脉动风具有时间和空间上的相关性，Fgy不能够像处理空气阻尼一样移动到等式的左端，只能够进行简化，将其当作外界激励，离散施加到接触线、承力索上。利用分离变量法求解，可化为如下形式

(35)

(36)

(37)

式中：Fgya和Fgyb分别为作用在承力索和接触线上的脉动风激励，计算方法可参见式(33)，Ls为离散单元长度。在下节的算例中，每隔16 m取一个点，12跨京津线接触网则一共选取37个点作为脉动风气动力的施加点。

结合受电弓运动式(23)、式(24)，则可以构建计及脉动风激励的弓网动力学方程。

4.3 基于AR模型的脉动风模拟

在求解计及脉动风激励的弓网动力学方程之前，首先需要求得式(31)、式(32)中的顺风向和垂直于风向的脉动风时程u和w。文献[13-14]指出，同时具有时间相关性的AR模型能够更好的构建适合于铁路接触网结构的脉动风场，本节亦采用这种方法。

采用AR模型模拟脉动风时程时，Q个点空间相关脉动风速时程v(X,Y,Z,t)列向量可表述为[24]

(38)

X=x1,x2,…,x3,…,xQT

Y=y1,y2,…,y3,…,yQT

Z=z1,z2,…,z3,…,zQT

式中：xi,yi,zi为空间点i的坐标；W为AR模型的最大阶数；Δt为模拟脉动风的时间步长；φk为k阶AR模型自回归系数矩阵；N(t)为独立随机过程向量。

文献[28]指出4阶AR模型能够足够精确地模拟脉动风速时程，本文分别选取Davenport谱和Panosfky谱模拟顺向和垂向脉动风时程。具体参数选取可参考文献[13-14]。

以本文的京津线12跨接触网为例，每16 m取1个点，一共37个点，图7、图8为平均风速为30 m/s时，第1点的顺向和垂向脉动风时程仿真时程以及和目标谱的比对结果,从图中可以看出仿真谱和目标谱重合度很高，AR模型能够很好地反映出脉动风的频域特性。

根据上节的推导和计算，将不同风速的脉动风激励施加到弓网动力学方程中，并利用Newmark法进行求解，可得到接触压力的时程，本节将分别从时域和频域角度研究风速对接触力的影响，并考虑风攻角的影响，研究相同风速下不同攻角对受流的影响。

4.4 风速对接触压力时域特性的影响

图9为风攻角保持40°不变时，风速分别为5、10、30 m/s时的弓网间的接触压力曲线，表5为其时域统计量。

从图9和表5中可以看出。在脉动风激励下接触压力最小值减小量和最大值的增加量都较为明显。当风速为5 m/s时，接触压力统计量相比于无风情况变化不明显，此时脉动风对弓网受流特性的影响很小。但达到10 m/s时，脉动风激励对弓网受流的影响已经较为显著，尤其是方差的增加体现了接触力波动的增大，将导致接触线的疲劳可靠性下降。风速达到30 m/s时，弓网受流已十分恶劣，峰值达到419.25 N，弓网出现离线，弓网间电弧频繁产生，易造成供电中断和接触线烧伤，对弓网安全运营造成了威胁。

表5 不同风速下弓网接触压力统计量

风速/(m·s-1) 接触压力统计量 最大值/N最小值/N平均值/N标准差/N离线率0308．01762．24189．6541．0905314．7045．22189．7440．63010339．2940．79189．9449．16030419．250190．0073．530．016

4.5 风速对接触压力频域特性的影响

脉动风激励对弓网接触力的影响除了表现在时域统计量上以外，还会对接触力的频谱特性造成影响。本节分别对不同风速下的接触力进行快速傅里叶变换，得到接触力的频谱图。图9绘制了无风时的接触力频谱和风速为5 m/s时的接触力频谱，图10绘制了风速为5 m/s时和30 m/s时的接触力频谱。

从图10中可以看出，脉动风激励对接触压力各频域上的能量均有一定的影响，从图11可以看出，风速增加至30 m/s后，接触压力在整个频域上的能量值有明显的提升，相当于对弓网系统注入扰动能量，使其振幅有明显的提升。

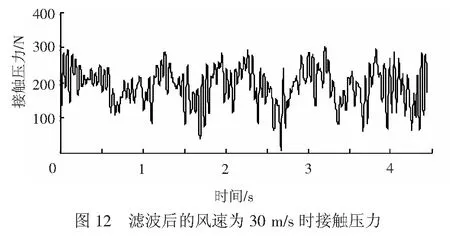
在研究弓网受流特性时，常常对仿真接触压力进行20 Hz的低通滤波，如文献[29]等。本文同样将30 m/s脉动风下的接触压力进行滤波，如图12，可以看到很多离线现象和许多峰值突变都观察不到，因此，由于脉动风的高频特性，在研究环境风下的弓网受流时，不宜对接触力进行滤波处理。

4.6 风攻角对接触压力的影响

根据前文的推导可知，脉动风对接触压力的影响主要是通过施加在弓网动力学方程右端的脉动风激励载荷Fgya和Fgyb导致的，为研究风攻角对弓网受流的影响，首先探讨施加在接触线上的气动力Fgyb随攻角的演变规律，选取施加在第一点上的气动力为研究对象，图13为风速保持10 m/s不变时，作用在第一点上气动力绝对值最大值、平均值、标准差随风攻角的演变曲线。绝对值最大值和平均值体现了脉动风激励的整体强度，标准差体现了脉动风的离散程度，很显然，脉动风的整体强度越强、离散程度越大对弓网的受流越不利。从图13可以看出，对弓网受流最有利的理想风攻角在0～20°之间，其标准差最小，绝对值最大值和平均值都在0附近，此时，环境风接近于水平风，主要影响接触网的横向振动，对竖向上的受流影响较小。为验证这一结论，图14为风速10 m/s时，风攻角分别为0°、20°和60°时的接触压力。表6为其统计量。

从表6和图14中可以看出，0°和20°风攻角下的接触压力方差明显小于攻角60°时，最大值与最小值之差也小于攻角60°时，因此，0°和20°攻角下接触压力的波动小于攻角60°时，可见，来流风越趋近于水平方向，对受流越有利。

表6 不同风攻角下弓网接触压力统计量

风攻角/(°)接触压力统计量最大值/N最小值/N平均值/N标准差/N最大值与最小值之差/N0306．0849．92189．5639．53256．1520327．1526．15189．7339．68300．9960326．6718．04190．2444．08308．63

5 结论

论文分别研究了静风载荷产生的空气阻尼和脉动风载荷的外界激励对弓网受流的影响，经过比较发现，静风载荷引起的空气阻尼对弓网受流影响不大，可忽略不计。但是脉动风载荷的影响十分明显，脉动风对弓网受流特性的影响主要体现在以下几个方面：

(1) 弓网受流质量随脉动风速增加而变差。当风速达到30 m/s时，离线已较为严重。

(2) 通过对接触压力的频谱分析发现，在研究计及环境风的弓网受流时，不宜对接触压力进行滤波处理；风速的增加相当于对弓网系统注入的扰动能量增大，会导致接触压力频谱能量的整体增加。

(3) 经过研究风攻角对接触压力的影响发现，风速一定时，来流风越偏水平方向，越有利于弓网受流。在本文算例中，0～20°是对受流最有利的理想的攻角。

本文从理论推导出发，基于模态分解法修正了计及接触网空气动力的弓网动力学方程，可用于进一步研究气动载荷对弓网动态特性的影响，也可为接触网防风设计提供借鉴。

参考文献：

[1] 于万聚. 高速电气化铁路接触网[M]. 成都:西南交通大学出版社, 2003.

[2] ZHOU Ning, ZHANG Weihua. Investigation on Dynamic Performance and Parameter Optimization Design of Pantograph and Catenary System[J]. Finite Element in Analysis and Design, 2011, 47(3): 288-295.

[3] ARNOLD M, SIMEON B. Pantograph-catenary Dynamics: a Benchmark Problem and its Numerical Solution[J]. Applied Numerical Mathematics, 2000, 31(4): 345-362.

[4] 于万聚, 王晓保. 高速铁路-受电弓系统动态受流特性的仿真研究[J]. 铁道学报, 1991,13(S1): 9-18.

YU Wanju, WANG Xiaobao. Emulation Researches on the Dynamic Current-collection Characteristics of the Pantograph-catenary Contact System on High-speed Railway Lines[J]. Journal of the China Railway Society, 1991,13 (S1): 9-18.

[5] 梅桂明, 张卫华. 受电弓/接触网系统动力学模型及特性[J]. 交通运输工程学报, 2002, 2(1): 20-25.

MEI Guiming, ZHANG Weihua. Dynamics Model and Behavior of Pantograph/Catenary System[J]. Journal of Traffic and Transportation Engineering, 2002, 2(1): 20-25.

[6] ZHAI W M, CAI C B. Effect of Locomotive Vibrations on Pantograph-catenary System Dynamics[J]. Vehicle System Dynamics, 1998, 29(S1): 47-58.

[7] BOCCIOLONE M, RESTA F, ROCCHI D, et al.Pantograph Aerodynamic Effects on the Pantograph-catenary Interaction[J]. Vehicle System Dynamics, 2006, 44(S1):560-570.

[8] 蔡国华. 高速列车受电弓气动力特性测量[J]. 流体力学实验与测量,2004,18(1):53-56.

CAI Guohua. Aerodynamic Characteristic Measurements on Pantograph of Super Express Train[J].Experiments and Measurements in Fluid Mechanics, 2004, 18(1):53-56.

[9] 曹树森, 邓斌, 马素君,等. 接触线风振疲劳可靠性分析[J]. 机械科学与技术, 2011, 30(10): 1 664-1 668.

CAO Shusen, DENG Bin, MA Sujun, et al. Fatigue Reliability Analysis of Contact Wire under Wind Load[J]. Mechanical Science and Technology for Aerospace Engineering, 2011, 30(10): 1 664-1 668.

[10] 吴家岚. 高速铁路接触网风致响应分析[D]. 成都: 西南交通大学, 2008: 42-70.

[11] 赵飞, 刘志刚, 韩志伟. 随机风场对弓网系统动态性能影响研究[J]. 铁道学报, 2012, 34(10): 36-42.

ZHAO Fei, LIU Zhigang, HAN Zhiwei. Simulation Study on Influence of Stochastic Wind Field to Dynamic Behavior of Pantograph-catenary System[J]. Journal of the China Railway Society, 2012, 34(10): 36-42.

[12] 刘志刚, 侯运昌, 韩志伟, 等. 基于风场模拟的高铁接触网动态性能分析[J].铁道学报,2013,35(11):21-28.

LIU Zhigang, HOU Yunchang, HAN Zhiwei, et al. The Dynamic Characteristics Analysis of High-speed Railway Catenary based on Wind Field Simulation[J]. Journal of the China Railway Society 2013, 35(11):21-28.

[13] 李瑞平, 周宁, 张卫华, 等. 基于AR模型的接触网脉动风场与风振响应[J]. 交通运输工程学报, 2013, 13(4): 56-62.

LI Ruiping, ZHOU Ning, ZHANG Weihua, et al. Fluctuating Wind Field and Wind-induced Vibration Response of Catenary based on AR Model[J]. Journal of Traffic and Transportation Engineering, 2013, 13(4): 56-62.

[14] 李瑞平, 周宁, 吕青松, 等. 横风环境中弓网动力学性能分析[J]. 振动与冲击, 2014, 33(24): 39-44.

LI Ruiping, ZHOU Ning, LV Qingsong, et al. Pantograph-catenary Dynamic Behavior under Cross Wind[J]. Journal of Vibration and Shock, 2015, 33(24): 39-44.

[15] POMBO J, AMBROSIO J. Environmental and Track Perturbations on Multiple Pantograph Interaction with Catenaries in High-speed Trains[J]. Computers and Structures, 2013, 124: 88-101.

[16] POMBO J, AMBROSIO J, PEREIRA M, et al. Influence of the Aerodynamic Forces on the Pantograph-catenary System for High-speed Trains[J]. Vehicle System Dynamics, 2009, 47(11): 1 327-1 347.

[17] 宋洋, 刘志刚, 汪宏睿, 等. 脉动风下高速铁路接触网抖振对弓网受流性能的影响[J]. 铁道学报, 2014, 36(6): 27-34.

SONG Yang, LIU Zhigang, WANG Hongrui,et al. Influence of High-speed Railway Catenary Buffeting on Pantograph-catenary Current Collection under Fluctuating Wind[J]. Journal of the China Railway Society, 2014, 36(6): 27-34.

[18] 宋洋, 刘志刚, 汪宏睿. 覆冰接触线气动系数研究与风振响应分析[J]. 铁道学报, 2014, 36(9): 20-27.

SONG Yang, LIU Zhigang, WANG Hongrui. Study on Aerodynamic Parameters and Wind Vibration Responses of Iced Contact Wires of High-speed Railways[J]. Journal of the China Railway Society, 2014, 36(9): 20-27.

[19] 侯运昌, 刘志刚, 宋洋, 等. 基于索, 杆组合结构的电气化铁路接触网三维静态模型[J]. 铁道学报, 2014, 36(7): 24-29.

HOU Yunchang, LIU Zhigang, SONG Yang, et al. Modeling of Steady State of Electric Railway Catenary Based on Nonlinear Cable and Truss[J]. Journal of the China Railway Society, 2014,36( 7): 24-29.

[20] 宋洋, 刘志刚, 汪宏睿, 等. 接触网三维模型的建立与风偏的非线性求解[J]. 铁道学报, 2015,37(4): 30-38.

SONG Yang, LIU Zhigang, WANG Hongrui, et al. Establishment of 3D Model for Catenary and Nonlinear Solution for It’s Wind Deflection[J]. Journal of the China Railway Society, 2015,37(4): 30-38.

[21] 刘志刚, 韩志伟, 侯云昌,等. 计及空气阻尼影响的接触线波动速度修正研究[J]. 铁道学报, 2013, 35(1): 41-45.

LIU Zhigang, HAN Zhiwei, HOU Yunchang, et al. Modified Formula of Wave Motion Velocity of Catenary Inclusive of Air Damping[J]. Journal of the China Railway Society, 2013, 35(1): 41-45.

[22] DESAI Y M, SHAN A H, POPPLEWELL N. Perturbation Based Finite Element Analyses of Transmission Line Galloping[J]. Journal of Sound and Vibration, 1996, 191(4):469-489.

[23] 李丰良, 粟谦. 接触网的力学模型及运动微分方程[J]. 长沙铁道学院学报,1996, 14(2):90-93.

LI Fengliang, SU Qian. The Dynamic Model and Differential Equations of the Catenary [J]. Journal of Changsha Railway University,1996, 14(2):90-93.

[24] 刘煜铖, 刘志刚, 宋洋,等. 高速铁路接触线静态气动力参数仿真计算研究与风洞试验[J]. 铁道学报, 2014, 36(5): 33-38.

LIU Yucheng, LIU Zhigang, SONG Yang,et al. Simulation Calculation and Wind Tunnel Test of Static Aerodynamic Parameters of High-speed Railway Contact Line[J]. Journal of the China Railway Society, 2014, 36(5): 33-38.

[25] 王少华, 蒋兴良, 孙才新. 覆冰导线舞动特性及其引起的导线动态张力[J]. 电工技术学报, 2010, 25(1): 159-166.

WANG Shaohua, JIANG Xingliang, SUN Caixin. Characteristics of Icing Conductor Galloping and Induced Dynamic Tensile Force of the Conductor[J]. Transactions of China Electrotechnical Society, 2010, 25(1): 159-166.

[26] 赵飞, 刘志刚, 张晓晓. 基于有限元的高速弓网系统动态性能研究[J]. 铁道学报, 2012, 34(8): 33-38.

ZHAO Fei, LIU Zhigang, ZHANG Xiaoxiao. Simulation of High-speed Pantograph-catenary System Dynamic Performance Based on Finite Element Model[J]. Journal of the China Railway Society, 2012, 34(8): 33-38.

[27] 王之宏. 风载荷的模拟研究[J]. 建筑结构学报, 1994, 15(1): 44-52.

WANG Zhihong. Simulation of Wind Loading[J]. Journal of Building Structures, 1994, 15(1): 44-52.

[28] 胡雪莲, 李正良, 晏致涛. 大跨度梁结构放在和模拟研究[J]. 重庆建筑大学学报, 2005, 27(3): 63-67.

HU Xuelian, LI Zhengliang, YAN Zhitao. Simulation of Wind Loading for Large-span Bridhe Structures[J]. Journal of Chongqing Jianzhu University, 2005, 27(3): 63-67.

[29] POMBO J, AMBROSIO J. Multiple Pantograph Interaction with Catenary in High-speed Trains[J]. Journal of Computational and Nonlinear Dynamics, 2012, 7(4): 1-7.