基于单相LCL脉冲整流器的高速铁路牵引网谐波谐振抑制方法

王隽龙， 宋文胜， 葛兴来， 张文明， 冯晓云

(西南交通大学 电气工程学院， 四川 成都 610031)

目前，交-直-交结构的电力机车和高速动车组已成为我国电气化铁路的主力车型，其优点是具有良好的牵引性能，功率因数高、谐波干扰小，牵引系统功率大、体积小、重量轻、运行可靠[1]。由于交流传动电力机车和动车组中的网侧变流器广泛采用脉宽调制(Pulse width modulation, PWM)技术，与直流传动机车相比，具有网侧电流谐波频谱宽、高次谐波不可忽略的特点[2-3]。高次谐波电流不仅影响列车电力牵引传动系统的性能，还可能成为牵引网谐振的激励源，导致牵引网产生谐波谐振现象[4]。2007年4月动车组在京哈线开行以来，牵引网谐振现象曾多次发生，造成牵引变电所并联在牵引母线上的电容器组多次跳闸[5]；2010年，我国京沪高铁联调联试试验中，谐振产生的过电压造成了车载避雷器击穿事故[6]。

因此，国内外相关学者对牵引网谐波谐振特性进行了广泛研究。文献[7]基于大量实测数据，采用曲线拟合和概率统计方法，建立了高速动车组谐波电流模型。文献[8-9]基于统一正弦切割模型分别分析了两电平和三电平高速列车高次谐波的产生机理，提出了高次谐波负荷的建模方法。文献[10]建立了牵引网-高速列车的耦合仿真模型，分析了列车所产生谐波电流沿接触网的放大特性，并确定了其放大谐振频率点。文献[6,11-12]将模态分析法从电力系统引入牵引供电系统中，可确定系统谐振频率和各节点激励谐振能力及受谐振的影响程度。这些文献对谐振机理进行了深入的分析，为谐振抑制提供了理论指导。

然而，针对谐振抑制方面的工程设计较少。文献[13]提出在牵引网中安装由静止无功补偿器和混合有源滤波器组成的并联混合补偿装置，从而对谐波谐振进行抑制，这种抑制方案的本质是改变牵引网线路阻抗参数实现谐振频率的转移。由于谐波谐振现象是列车和牵引网耦合下出现的问题，因此抑制谐波谐振既可通过调节牵引网参数转移谐振频率来实现，也可通过消除谐波源，即减少机车电流中的特定次谐波含量实现。文献[14-15]通过优化网侧脉冲整流器和电机侧PWM逆变器的调制模块开关角，以抑制相应谐振谐波的幅值。文献[16]提出在牵引变压器二次侧增加一个电力电子谐波补偿装置，用于补偿和吸收牵引主传动系统对牵引网产生的谐波，从而减少车网谐波谐振现象的发生。但这两种方法均需要对谐振频率进行在线辨识，工程实现与应用较为困难。

采用LCL滤波的脉冲整流器谐波抑制效果好，并可以减小网侧电感量、降低开关频率，在风力发电及电力传动领域具有广泛的应用前景[17]。文献[18]基于脉冲整流器的稳定性和动态性能给出了LCL滤波器的参数设计方法。文献[17,19]给出了三相LCL滤波的脉冲整流器优化控制策略。但上述研究均基于三相LCL脉冲整流器，对单相LCL脉冲整流器的参数设计和控制策略还有待进一步研究。

本文首先对高速铁路牵引网的谐波谐振机理进行分析，给出谐振危害度与机车谐波电流大小的关系。在此基础上，从列车车载设备的角度出发，以抑制和消除谐波激励源为目的，提出一种网侧单相LCL型脉冲整流器拓扑，并给出了该脉冲整流器的控制算法。最后，搭建牵引网-列车联合仿真系统，对其谐振抑制效果进行仿真验证。

1 牵引网谐波谐振机理

为保证列车高速运行，我国高速铁路主要采用全并联自耦变压器(auto-transformer, AT)供电技术，与直接供电、吸流变压器等供电方式相比，其电压等级高、供电臂长，对邻近通信线路干扰较小[20]。但AT供电系统结构复杂，如果对各元件和导线单独考虑，则牵引网谐振机理分析将非常困难。本文根据文献[5]，引入牵引网单线简化模型，考察谐振点分布和谐波传播规律。

图1给出了单线等效牵引供电系统谐波分析模型，其中Zss为牵引变电所电源电抗；IT为机车电流；l1为机车到变电所距离；l2为机车到分区所距离。机车负荷是牵引网的主要谐波源，当交-直-交列车在牵引网运行时，可将列车等效为电流源。

根据电力传输线稳态方程和等值电路，对机车两边的传输线采用T型电路进行等效，见图2，可以得出

( 1 )

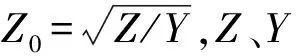
从机车所在位置来看，牵引网输入阻抗Zp为

( 2 )

式中：l为牵引网总长度，l=l1+l2。

当式( 2 )中分母为0或接近0时，牵引网阻抗取得极大值，因此谐振条件可以表示为

Zsssinhγl+Z0coshγl=0

( 3 )

由于γl≪1，因此tanhγl≈γl，式( 3 )可进一步简化为

( 4 )

式中：Lss为牵引变电所等效电感 ；wpr为谐振角频率；Zss=wprLss,；C=cl，近似为整个线路的总电容，c为单位长度线路分布电容。则系统的谐振频率fpr为

( 5 )

由上述分析可知，牵引网谐振现象可近似等效为牵引变电所等效电感与牵引网分布电容构成的并联谐振。式( 5 )表明谐振频率主要由牵引网自身参数决定，与列车位置无关。

当高速列车或电力机车将谐波电流注入牵引网时，牵引网会受到特定次谐波电流的激励而发生谐振，引起谐波电流的放大。设IX为距离机车X处的牵引网电流，则通过计算得到

( 6 )

式中:In为机车电流IT中的谐波电流。

设谐振放大系数为λ，则

( 7 )

当列车位置确定时，在特定距离机车X处来看谐振放大系数λ为常数，因此IX与In可近似等效为比例关系。此时若要减少谐波电流IX，可通过减少注入机车中谐波电流In大小来实现。

高速列车与电力机车的牵引传动系统功率都较大(约8～10 MW)，受限于现有高压、大电流的应用场合，牵引变流器的开关频率都较低(约1.5 kHz以内)，因此传统单相L型脉冲整流器交流侧输入电流谐波含量高，且主要为由开关器件切换产生的高次谐波分量[7]。由式( 6 )可知，电流中的高次谐波可能成为牵引网谐波谐振的激励源。若能够大幅减小甚至消除谐振频率点附近谐波电流In，则由于激励源强度，牵引网仅发生轻微的谐波谐振现象，不会对牵引供电系统和牵引传动系统的正常运行造成影响。

2 LCL单相脉冲整流器建模和控制系统设计

现有动车组牵引传动系统在变流器前端广泛采用单电感L型滤波器对网侧电流进行滤波，这种方法对高次谐波滤除效果相对较差。相比于传统L型滤波器，LCL滤波器具有三阶的低通滤波特性，在同样谐波标准和较低的开关频率下， LCL滤波器能够有效滤除网侧电流中的高次谐波[18]。

2.1 LCL滤波的脉冲整流器数学模型

图3为单相脉冲整流器主电路，网侧采用LCL滤波器取代传统L滤波器。图中：Lg为牵引变压器二次侧等效电感；L为变流器侧电感；Cf为滤波电容；Cd为直流侧支撑电容；RL为负载等效电阻；us为网侧电压；ig为网侧电流；i为变流器侧电流；uc为滤波电容电压；udc为直流电压；idc为直流侧负载电流。

对于图3 所示的主电路，根据基尔霍夫电压定律(Kirchhoff's Voltage Law,KVL)和电流定律(Kirchhoff's Current Law,KCL)，该脉冲整流器的数学模型可以表示为

( 8 )

( 9 )

(10)

(11)

式中:S为整流桥的等效开关函数，且S∈[-1,1]。

联立式( 8 )～式(11)，可得到该脉冲整流器数学模型的状态方程

(12)

式中:XT=(ig,uc,i,udc)，B=(1,0,0,0)T

2.2 LCL滤波的脉冲整流器控制系统设计

脉冲整流器作为电力牵引传动系统的网侧变流器，主要完成两大控制目标：第一，直流侧电压保持在允许的偏差范围内；第二，网侧功率因数接近于1(牵引工况)或-1(再生制动工况)。

2.3 LCL滤波器参数设计

LCL滤波器的参数设计较为复杂，设计不合理时不仅达不到预期的滤波效果，反而会增加电流畸变，造成系统的崩溃。本文参考三相脉冲整流器LCL滤波器的设计方法[18]，给出了单相脉冲整流器LCL滤波器的设计限制。

(1) 滤波器等效总电感LT的限制

从稳态条件下脉冲整流器输出有功(无功)能力考虑，LCL滤波器的总电感量LT(LT=Lg+L)应予以限制，其计算式为

(13)

式中：fn为基波频率；Us为网侧电压有效值；ILP为网侧电感电流的峰值。

(2) 滤波电容Cf的限制

为了保证整流器单位功率因数，滤波电容吸收的无功功率Qc一般不大于系统额定功率的5%，故可得出电容的吸收功率

(14)

令Qc=5%Pn，因此有

(15)

式中：Pn为单个脉冲整流器额定功率。

(3) 谐振频率fres的限制

LCL滤波器的谐振频率fres一般设计在10倍基频fn至开关频率fr之间，即有

10fn≤fres≤fr

(16)

3 牵引网-机车联合仿真系统

3.1 牵引网仿真模型

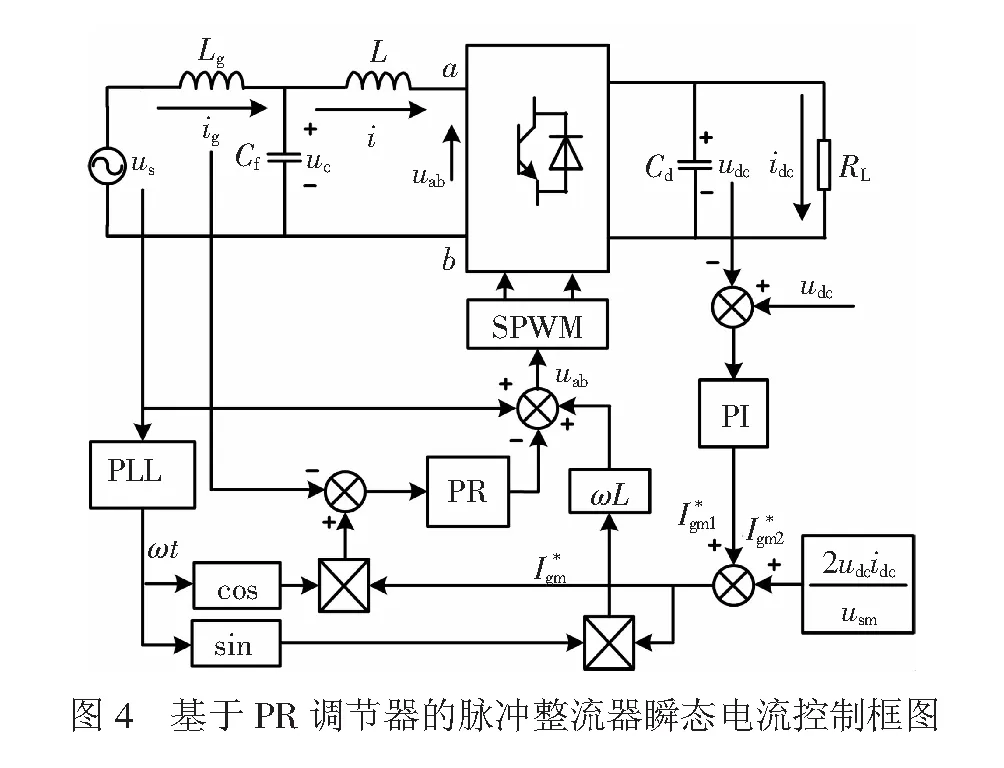
全并联AT牵引供电网结构复杂，主要由变电所(power substation, PS)、AT所(AT post, ATP)、分区所(section post, SP)及多导体传输线组成。多导体传输线主要由承力索、接触线、加强线、正馈线、钢轨、地线及保护线组成。在仿真计算中，若对各导线单独考虑，则导线数目较多，计算复杂。实际应用中，一般采用降阶的方法，将电气相连的导线等效为一根导线。本文分上下行线路分别将承力索、加强线与接触线等效为接触线；地线、保护线与钢轨等效为钢轨。因此AT牵引网多导体传输线可等效为6导体传输线，分别为上下行接触线(contact line, C)、钢轨(rail, R)、馈线(feeder, F)；同时将上下行线路在变电所、AT所和分区所通过横向连接线将接触网、钢轨、馈线并联连接，使上下行线路共用变压器。

图5为本文选取的AT供电牵引网左供电臂示意图。变电所接入交流220 kV三相公共电网，其变压器采用单相V/v接线。牵引网供电臂长19.1 km，区间有1个AT所，与变电所距离为11.2 km；有1个分区所，与AT所距离为7.9 km。

由于变电所、AT所、分区所与列车等横向并联元件之间距离小于15 km，高精度的π等值电路即可对相邻横向并联原件间多导体传输线进行较精确的建模，因此横向并联元件可用于牵引网的自然“切割”建模。

利用横向并联元件对牵引网的自然“切割”进行建模，切割后牵引网包含1、2、3、4四个切面，见图5。各切面横向并联元件可等效为导纳与电流源并联支路。相邻切面间多导体传输线用π等值电路连接。因此图5所示的牵引网可表示为图6所示的链式网络结构，图中各电气量均为6维矩阵。

根据上述内容，本文在Matlab/Simulink中建立了牵引供电系统仿真模型，其结构见图7。其中uc、ur、uf为上行的接触线、钢轨和馈线，dc、dr、df为下行的接触线、钢轨和馈线。为变电所部分由供电电源和变压器模块、等效并联导纳模块和短路连接线组成；6导体传输线采用Simulink库文件Distributed Parameters Line模型，输入为基于Carson理论计算得到的传输线分布参数[22]；AT所由短路连接线、自耦变压器(图中AT模块)组成；AT所和分区所之间的传输线分为4 km和3.9 km两部分，从上行接触线引出输出端①，从上行钢轨引出输出端②，用于连接动车组模块；分区所由短路连接线模块、自耦变压器和端部截断等效并联导纳模块组成。变电所、AT所与分区所中牵引变压器与AT、横向短路连接线、SP端部截断的等效并联导纳及传输线π等值电路的计算方法可以参考文献[22-23]。

3.2 高速动车组牵引传动系统等效模型

动车组是高速铁路牵引供电系统的主要谐波源，建立其精确的仿真模型有利于模拟动车组谐波特性和牵引网谐振特性。本文参考CRH3型动车组牵引传动系统结构，搭建了基于LCL滤波的高速动车组牵引传动系统等效模型。

图8给出了基于LCL脉冲整流器的基本动力单元示意图。如图所示，牵引变压器原边电流为is，次边电流为ig1与ig2；LCL滤波器由变压器漏感、滤波电感Cf、变流器侧电感L组成；整流器A和B通过并联方式组成二重化脉冲整流器，可提高系统2倍的等效开关频率[1]；由于列车网侧高次谐波的形成主要由网侧变流器产生[8]，为了简化起见，直流侧的牵引逆变器-牵引电机系统近似等效为阻性负载。图中输入端①和输入端②分别与牵引网仿真模型上行的接触线及钢轨连接，与牵引网仿真模型共同组合为联合仿真系统。

4 联合仿真对比验证

为了验证脉冲整流器的性能及其谐波谐振抑制效果，基于Matlab/Simulink搭建基于LCL滤波的二重化脉冲整流器和全并联AT供电系统的联合仿真模型，并在同一牵引网下与单电感滤波的二重化脉冲整流器进行仿真对比。

牵引供电系统采用的仿真参数见表1；牵引传动系统采用的仿真参数参考CRH3型动车组牵引传动系统，LCL滤波器参数由2.3节设计得出，其仿真参数见表2。

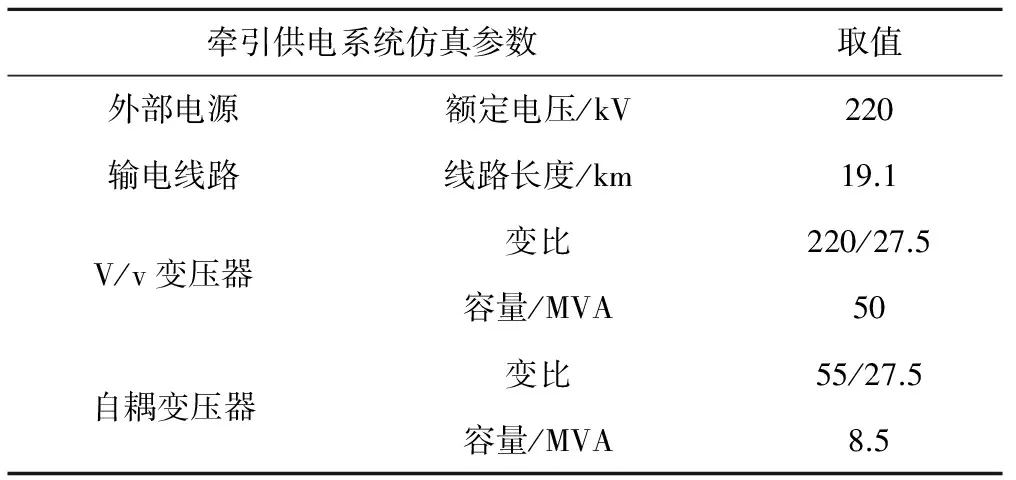
表1 牵引供电系统仿真参数

表2 牵引传动系统仿真参数

图9给出了在100%额定功率情况下，基于单电感L滤波(滤波电感Ls=Lg+L)的仿真结果。图9(a)为变压器二次侧电压us和电流ig的仿真波形，可以看出电压和电流同相位，实现了单位功率因数。图9(b)为网侧电流的频谱特性，其THD值为10.64%，谐波主要为1 100 Hz(2倍开关频率)和2 200 Hz(4倍开关频率)附近的奇次谐波，其中1 050 Hz、1 150 Hz的谐波含量高达7.07%、6.47%。

图10给出了在100%额定功率情况下，基于LCL滤波的脉冲整流器的仿真结果。图10(a)为变压器二次侧电压us和电流ig的仿真波形，可以看出电压和电流同相位，实现了单位功率因数，网侧电流正弦度较好。图10(b)为网侧电流的频谱特性，其THD值为3.36%，谐波主要分布在1 050 Hz和1 150 Hz，含量分别为2.31%和1.85%。对比图9和图10可知，基于LCL滤波的脉冲整流器网侧电流波形更为平滑，2倍开关频率附近的高次谐波含量明显下降。

图11给出了100%额定功率下整流器二重化后对机车电流is的谐波分析，可以看出采用载波移相技术后分布在1 100 Hz附近的谐波已基本消除，机车电流的主要谐波分布在2 200 Hz附近。图11(a)为采用单电感滤波机车电流is的谐波分析， 其2 050 Hz、2 350 Hz的谐波含量较高，分别为1.34%、1.08%；图11(b)为采用LCL滤波机车电流is的谐波分析，其2 050 Hz、2 350 Hz的谐波含量分别为0.14%、0.11%，表明高次谐波得到了有效地抑制和消除。

当机车功率从10%到100%之间变化时，两种滤波器对应的机车电流谐波分析见图12所示，2种滤波器对应的机车电流高次谐波幅值的详细对比见表3。从图12和表3中可以得到，机车电流is的高次谐波幅值与机车功率基本无关，不同功率下基于LCL滤波方法的高次谐波幅值要远小于基于单电感滤波方法的高次谐波幅值。

表3 不同功率下机车电流高次谐波幅值对比

图13和图14给出了100%额定功率下L和LCL车载滤波器的牵引网-列车联合仿真结果。图13(a)为采用单电感滤波器对应的牵引网压波形，图13(b)为牵引网压的谐波分析结果。由于单电感滤波器对机车电流中的高次谐波滤波效果较差，这些高次谐波会激发牵引网产生谐波谐振现象，从图13(b)中可以看出牵引网压中高次谐波的含量较高，其中2 350 Hz的谐波含量达到30.74%。

图14(a)和图14(b)分别给出了加入LCL滤波器后，牵引网压的波形和其谐波分析结果。由图14(a)可看出加入LCL滤波器后，牵引网谐波谐振现象已经得到有效抑制，图14(b)所示谐波分析结果表明牵引网压中的高次谐波得到了很好地消除。

图15给出了机车功率从10%增大到100%时，牵引网压谐波分析的情况。图15(a)为基于单电感滤波的牵引网压情况，可以看到随着机车功率从10%增大到100%，2 350 Hz谐波电压峰值超过10 kV，牵引网发生了严重的谐振现象。图15(b)为基于LCL滤波的牵引网压情况，可以看到在2 350 Hz附近有轻微的谐振现象，但此时谐波幅值明显减小，牵引网谐波谐振现象得到了较好地抑制。

表4给出不同功率牵引网压高次谐波幅值对比。

表4 不同功率下牵引网压高次谐波幅值对比

结合表3可以看出采用LCL滤波器后，机车电流中的高次谐波虽然仍分布在谐振频率附近，但谐波含量大幅降低；牵引网压中谐振频率附近的谐波虽有明显放大，但谐波含量较低，对牵引供电系统和牵引传动系统的正常运行影响较小。

以上仿真结果表明，在脉冲整流器前端引入LCL滤波器后，机车电流中高次谐波含量大幅减小，消除了谐振的激励源，有效地抑制了牵引网谐波谐振现象。

5 结论

本文以电气化高速铁路面临的牵引网高次谐波谐振问题为研究对象，以谐振抑制为研究目的，提出了一种基于单相LCL型脉冲整流器拓扑的谐波谐振抑制方法，给出了该拓扑整流器的控制算法与LCL滤波器参数设计方法，开展了牵引网-列车系统耦合仿真验证。理论分析和仿真结果都表明：

(1) 牵引网谐波谐振是由于机车电流的主要谐波频率与牵引网谐振频率发生匹配时，网压发生严重畸变的现象。机车电流中的高次谐波是牵引网高次谐波谐振的激励源，可通过减少高次谐波含量实现谐振抑制；

(2) 与传统单电感滤波的脉冲整流器相比，在总电感参数相同情况下，单相LCL型脉冲整流器仅增加一个较小容值的电容，可有效地降低列车网侧电流的谐波含量，实现对牵引网高次谐波谐振的抑制。

参考文献：

[1] 冯晓云.电力牵引交流传动及其控制系统[M].北京：高等教育出版社，2009.

[2] 解绍锋, 李群湛, 赵丽平. 电气化铁道牵引负载谐波分布特征与概率模型研究[J]. 中国电机工程学报, 2005, 25(16): 79-83.

XIE Shaofeng, LI Qunzhan, ZHAO Liping. Study on Harmonic Distribution Characteristic and Probability Model of the Traction Load of Electrified Railway[J]. Proceedings of the CSEE, 2005, 25(16): 79-83.

[3] 高吉磊, 张雅静, 林飞, 等. 单相PWM整流器谐波电流抑制算法研究[J]. 中国电机工程学报, 2010, 30(21): 32-38.

GAO Jilei, ZHANG Yajing, LIN Fei, et al. Research on Harmonic Current Elimination Method of Single-phase PWM Rectifiers[J]. Proceedings of the CSEE, 2010, 30(21): 32-38.

[4] MOLLERSTEDT E，BERNHARDSSON B.Out of Control Because of Harmonics Analysis of the Harmonic Response of an Inverter Locomotive[J].IEEE Control Systems Magazine，2000，20(4)：70-81.

[5] 刘建强, 郑琼林, 杨其林.高速列车牵引传动系统与牵引网谐振机理[J]. 电工技术学报，2013, 28(4): 221-227.

LIU Jianqiang, ZHENG Qionglin, YANG Qilin.Resonance Mechanism Between Traction Drive System of High-speed Train and Traction Network[J]. Transactions of China Electro- technical Society, 2013, 28(4): 221-227.

[6] 崔恒斌，冯晓云，林轩，等.车网耦合下高速铁路牵引网谐波谐振特性研究[J].电工技术学报，2013，28(9)：55-64.

CUI Hengbin，FENG Xiaoyun，LIN Xuan，et al.Research of Harmonic Resonance Characteristic of High-speed Railway Traction Net Considering Coupling of Trains and Traction Nets[J].Transactions of China Electro-technical Society，2013，28(9)：55-64.

[7] 杨少兵, 吴命利. 基于实测数据的高速动车组谐波分布特性与概率模型研究[J]. 铁道学报, 2010, 32(3): 33-38.

YANG Shaobing, WU Mingli. Study on Harmonic Distribution Characteristics and Probability Model of High Speed EMU Based on Measured Data[J]. Journal of the China Railway Society, 2010, 32(3): 33-38.

[8] 崔恒斌，冯晓云，张杰，等.基于载波脉宽调制技术的牵引整流器谐波特性分析方法[J].电工技术学报，2013，28(8)：21-31.

CUI Hengbing，FENG Xiaoyun，ZHANG Jie.Harmonic Characteristic Analysis of Carrier Based Pulse-width Modulation Traction Converter[J].Transactions of China Electro-technical Society，2013，28(8)：21-31.

[9] CHANG G W, LIN H, CHEN S. Modeling Characteristics of Harmonic Currents Generated by High-speed Railway Traction Drive Converters[J]. IEEE Transactions on Power Delivery, 2004, 19(2): 766-773.

[10] 何正友，胡海涛，方雷，等.高速铁路牵引供电系统谐波及其传输特性研究[J].中国电机工程学报，2011，31(16)：55-62.

HE Zhengyou，HU Haitao，FANG Lei，et al.Research on the Harmonic in High-speed Railway Traction Power Supply System and its Transmission Characteristic[J].Proceedings of the CSEE，2011，31(16)：55-62.

[11] 王硕禾, 蔡清亮, 许继勇, 等. 基于模态分析的牵引供电系统谐波谐振过电压研究[J]. 铁道学报, 2013, 35(7): 32-40.

WANG Shuohe，CAI Qingliang，XU Jiyong，et al. Harmonic Resonance Over-voltage of Traction Power Supply System Based on Modal Analysis[J]. Journal of the China Railway Society, 2013, 35(7): 32-40.

[12] 胡海涛，何正友，钱澄浩，等.基于模态分析的全并联AT网动态谐波谐振研究[J].电网技术，2012，36(1)：163-169.

HU Haitao，HE Zhengyou，QIAN Chenghao.Modal Analysis Based Research on Dynamic Harmonic Resonance of All-parallel Autotransformer Traction Supply Network[J].Power System Technology，2012，36(1)：163-169.

[13] 张定华，桂卫华，王卫安，等.新型电气化铁道电能质量综合补偿系统的研究及工程应用[J].电工技术学报，2009，24(3)：189-194.

ZHANG Dinghua，GUI Weihua，WANG Weian，et al.Study and Application of a New Power Quality Combined[J]. Transactions of China Electro-technical Society，2009，24(3)：189-194.

[14] HOLTZ J, KRAH J O. Adaptive Optimal Pulse-width Modulation for the Line-side Converter of Electric Locomotives[J].IEEE Transactions on Power Electronics, 1992，7(1)：205-211.

[15] HOLTZ J, KRAH J O. Suppression of Time-varying Resonances in the Power Supply Line of AC Locomotives by Inverter Control[J]. IEEE Transactions on Industrial Electronics, 1992, 39(3): 223-229.

[16] KRAH J O, HOLTZ J. Total Compensation of Line-side Switching Harmonics in Converter-fed AC Locomotives[J]. IEEE Transactions on Industry Applications，1995，31(6)：1264-1273.

[17] 王颖杰，伍小杰，戴鹏，等. 采用参数辨识及新型主动阻尼控制的LCL滤波脉宽调制整流器[J]. 中国电机工程学报, 2012, 32(15): 31-39.

WANG Yingjie, WU Xiaojie, DAI Peng，et al.PWM Rectifier with LCL Filter Based on Parameter Identification and a New Active Damping Control[J]. Proceedings of the CSEE，2012, 32(15): 31-39.

[18] MARCO L，FREDE B，STEFFAN H.Design and Control of an LCL-filter Based Three-phase Active Rectifier[J].IEEE Transactions on Industry Applications，2005，41(5)：1281-1291.

[19] 何良，赵继敏，谢海先.三相电压型脉宽调制整流器的LCL滤波器设计[J].电网技术，2006，30(S1)：51-53.

HE Liang，ZHAO Jiming，XIE Haixian. The LCL Filter Design of Three-phase PWM Rectifier[J]. Power System Technology，2006，30(S1)：51-53.

[20] 吴命利.牵引供电系统电气参数和数学模型研究[D].北京：北京交通大学，2006.

[21] 王剑，郑琼林，高吉磊.基于根轨迹法的单相PWM整流器比例-谐振电流调节器设计[J].电工技术学报，2012，27(9)：251-256.

WANG Jian，ZHENG Qionglin，GAO Jilei.Design of Current Proportional-resonant Regulator for Single-phase PWM Rectifier Based on Root-locus Method[J].Transactions of China Electro-technical Society，2012，27(9)：251-256.

[22] 吴命利.电气化铁道牵引网的统一链式电路模型[J].中国电机工程学报，2010，30(28)：52-58.

WU Mingli.Uniform Chain Circuit Model for Traction Networks of Electric Railways[J].Proceedings of the CSEE，2010，30(28)：52-58.

[23] 李群湛，贺建闽.牵引供电系统分析[M].成都：西南交通大学出版社，2007.