数形有机结合关系自然求联——《平面图形的面积关系》教学设计与思考

张翼文（特级教师）

【教学目标】

1.知识技能：通过已学知识梳理，学生能自主地解答长方形、平行四边形、三角形与梯形面积的问题。

2.数学思考：通过经历画画、说说、想想等数学活动，学生能主动理解梯形的面积公式对于长方形、平行四边形、三角形的面积计算也是适用的。

3.问题解决：通过对长方形、平行四边形、三角形与梯形的面积公式的沟通，学生能主动地解决一些相关问题，以此促进数学推理能力的提升。

4.情感态度：通过数学探索活动，学生感受事物间的相互联系，并体验数形结合看问题的内在魅力，从而激发数学学习的兴趣。

【教学过程】

一、出示课题，谈话引入

师：今天我们一起来研究《平面图形的面积关系》，你看了这个课题后，你觉得哪个词是这节课的关键词呢？（板书：平面图形的面积关系）

生：我认为应该是“图形”。

生：我认为应该是“关系”。

生：我认为应该是“面积”。

师：同学看法不一致，那怎么办？

生：往下学习就可以知道了！

师：那我们就往下研究即可知。

【设计意图：课堂伊始，师生围绕课题进行简单对话，既能集中学生注意力，又能唤起探索的心向与欲望。】

二、回顾梳理，主动探索

1.知识的简单回顾与梳理。

（1）媒体出示，并说一说以下几种平面图形的面积计算公式。

（2）梳理展示。

S长方形=a×b

S平行四边形=a×h

S三角形=a×h÷2

S梯形 =（b+a）×h÷2

（3）问题暗示，引入探索。

师:这几个平面图形的面积计算过程中，你觉得哪个相对麻烦些呢？为什么？

生：我们认为梯形的面积计算相对麻烦些，因为，计算的步骤会多些。

师：今天就从计算相对比较烦的梯形面积公式开始研究，看能否给我们带来什么启示？

【设计意图：本环节对原有的几种平面图形的面积计算的知识进行简单回顾与梳理，这样面向全体的活动，可以夯实学生基础，起到温故而知新的效果。同时，在师生对话交流过程中，教师具有一定倾向性的问题暗示，可以进一步激发学生的探索欲望，为课堂后续学习注入热情。】

2.任务驱动，实践操作。

（1）任务驱动。

活动要求：请在下面格子图内画出高为4厘米，面积为20平方厘米的梯形。

（每个小正方形的边长为1厘米。）

（2）自主实践。（略）

（3）汇报交流。

师：完成这个作品前，你们是怎么想的呢？

生：我是用梯形公式倒过来推算的，求出梯形的上下底之和（即面积20乘2除以高4，得到上下底之和为10），然后确定上底为4，下底为6，最后再画的。

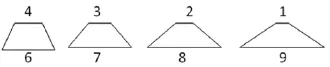
（4）展示作品。

师：老师也准备好这四幅作品，为了便于看清楚，老师已经按等比例扩大。

（逐一把四幅作品展示黑板上）

【设计意图：本环节通过画梯形这一任务驱动，促使学生对计算梯形面积相关知识的有意回忆，过程中学生进行有序地思考，学习任务完成的过程即思行合一的过程，进一步使学生知其然亦知其所以然。】

三、问题驱动，沟通联系

1.对话感知，引发思考。

师：上下底之和为10，高为4的梯形，只能画出这四幅作品吗？

生：如果梯形上下底的长度不一定是整数，可以是小数的话，那就有很多可能？

师：你们明白他刚才说的意思吗？你们能举例说明吗？

生：上底为3.5,下底为6.5,高为4。

生:上底为1.8,下底为8.2,高为4。

……

师:有多少种呢?

生:有无数种情况。

……

【设计意图：此环节通过启发式的引导，顺其自然地促进学生解决问题所需采集的数据从整数向小数延伸，伴随着学生的思维就由局限走向开放，彰显了课堂动态推进的过程中变与不变、有限与无限的关系。】

2.问题跟进，素材展现。

师：如果老师也来说几种，可以吗？

生：赞同！

师：上底为 0.9，下底为 9.1，高为 4；（实物展示黑板上，并标把上下底数据标上）

上底为0.8,下底为9.2,高为4;

上底为0.2,下底为9.8,高为4;

上底为0.1,下底为9.9,高为4。

……

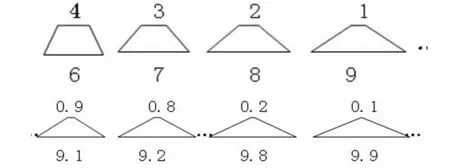
【设计意图:此环节通过师生对话，教师适机有选择地展现一些梯形,并标有相关数据,为接下来,学生进行长方形、平行四边形、三角形与梯形的面积计算公式进行有效沟通提供直观的素材。换句话说，也就是要促进学生思维走向深刻是需要教师帮助学生搭建“脚手架”的。】

3.数形结合，观察发现。

师：请仔细观察以上一组梯形，你有什么发现，或有什么想说的吗？

生：从左往右看，我发现梯形的上底越来越短，下底越来越长。

生：从左往右看，我发现梯形越来越像三角形了。

师：大家都观察到了吗？

（学生点头默许）

师：你们是怎么看出来的呢？

生：我是从并排梯形样子看出来的。

生：我发现，如果梯形上底越来越短，越来越短，它就会变成三角形。

生：我不太同意他的观点，因为梯形上底尽管越来越小，越来越小，但是再小，还是有长度的，只是我们看图形像三角形，实际上还是梯形。

师：你们同意他的观点吗？

（学生点头表示同意）

师：你们很会观察与思考，这正如华罗庚先生所说“数缺形少直观，形缺数难入微”。如果我们单从形看，越往右的梯形肉眼看就是三角形，如果看上下底提供的数据来看，哪怕上底越来越小，但是它还是梯形，只有当数与形结合起来看，我们来分析问题就会更合理。

……

【设计意图：从环节中可以看出，学生在课堂中精彩对话源自于适合的素材，本环节提供一组上下底标有变化数据的梯形实物图，帮助学生可以数形结合进行有效观察，并发现梯形与三角形之间的微妙关系，以此适机进行梯形面积公式适用于三角形的面积计算的有效沟通。以此真正意义上落实“数缺形少直观，形缺数难入微”之数形结合帮助学生进行合情推理的课堂教学理念。】

4.适机整合，沟通联系。

（1）引导沟通。

师：大家刚才发现，越往右梯形的上底越来越小，如果我把梯形上下底标上字母（在展示的图形上标出）。上底越来越小，也就是上底A点与B点慢慢逼近，AB点之间的距离越来越小，距离越来越接近“0”，如果 AB点距离为“0”时，那梯形就成为三角形；这时候三角形的面积可以怎么计算呢？

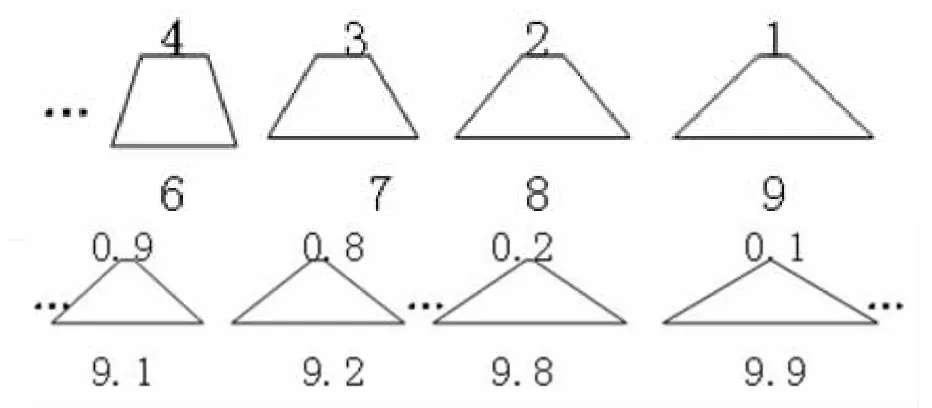
生：（0+10）×4÷2。

（2）自主求联。

师：梯形的面积公式也适用于三角形的面积。

（并规范板书 S三角形 =（b+a）×h÷2(b=0)）

（3）整体求联。

师：从左往右来看以下梯形的上底不断变长，如果继续增长，梯形又可能变成什么图形呢？

生：平行四边形。

师：那么梯形的面积也适用于平行四边形。

（板书示意沟通梯形、三角形、平行四边形、长方形的面积关系图）

（4）适机点题。

师:到现在为止,你明白这个课题的关键词应该是什么呢?

生:应该是“关系”！（异口同声地说）

【设计意图：此环节通过适当的问题驱动，引领学生静态观察与动态思考，从而促进梯形面积公式适应于三角形、平行四边形与长方形的面积计算进行“无缝”对接，正如苏格拉底所描写的教师好似“助产师”，教学行进过程中不断助推学生的学习引向深处。】

四、学以致用，解决问题

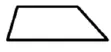
1.基础性练习。

下面四个图形的面积相等，另外三个图形的底是多少？（口答）

2.实践性练习。

（1）在上底为8，下底为10的梯形中添上一条线，使它分成两个面积相同的部分，你有几种不同的画法？并用数据表示出结果。

（2）把上底为8，下底为10的梯形分成面积相等的平行四边形、三角形与梯形的三部分，你能完成吗？并用数据表示出结果。

3.综合性练习。

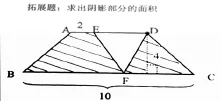
拓展题：求出阴影部分的面积

【设计意图：练习设计应该体现一定的层次性和灵活性。目的之一是夯实学生的基础，基础知识和基本技能是学生发展的根本，教学中不能淡化；另一方面让学生的思维走向深刻，着眼学生的后续发展。】