让学生与“距离”没有距离——《点到直线的距离》教学设计（一）

王敏烽/ 方巧娟

【教学内容】

人教版四年级上册第五单元第59页例3。

【课前思考】

本课教材编排首先通过引导学生把直线外一点A和水平方位的直线上任意一点连起来，通过实际测量得出“从直线外一点到这条直线所画的垂直线段最短”，并引出点到直线的距离的概念；然后利用画点到直线的垂线的经验，尝试画出平行线之间的垂直线段，并通过测量发现平行线之间的垂直线段长度相等。

通过前测发现，学生对于水平方位的直线外一点找最短线段和发现两条平行线内的距离处处相等的规律并不难。如果点到直线的距离只停留在水平方位直线的认识，概念建立是不完整的，对后续高的认识是非常不利的。因此，笔者将主例题调整为通过情境方式引入找斜线外一点的最短线段展开研究。经历“找出一条线段——找出无数条线段——垂直线段——垂直线段最短——垂直线段长度即距离”的过程认识距离，结合验证、辨析、动手画、判断等方式巩固距离，同时还结合生活进一步连接数学和生活之间的关系。

【课中探索】

一、出示图例，明确研究方向

出示森林地图：

1.猜测研究对象：图上你看到了什么？

2.抽象研究对象：在这幅森林地图上，你能找到点和直线吗？

3.小结：羊村可以用点O来表示，马路可以用直线m表示。（课件抽象画出点O和直线m）今天我们继续来研究有关于点和直线的知识。

【设计意图：从生活实际问题介入，把大路和房子抽象成数学中的点和线，让学生感受到生活问题解决中我们可以把问题先进行抽象，同时也为后续的问题解决做好孕伏。】

二、围绕核心，落实距离本质

1.找线段：慢羊羊村长打算在羊村O和马路m之间修一条小路，小路的一端在点O，另一端应该在哪？你会怎么修小路？

（指名修一条小路，画出线段）

2.找出无数条线段：还可以怎么修？

（学生指，教师画）

小结指出：从O点出发到直线m上任意一点的线段就是小路，并且这样的线段有无数条。

【设计意图：将例题中水平方向的小路调整为斜方向的小路，意在增加探究难度，减少“水平竖直哪条最短”对学生造成的负面影响，同时也增加了“哪条最短”的探究难度，提升了画垂直线段的价值。本环节重在明确“距离”是从某一点出发到某一点结束的线段。】

3.找出最短线段。

在学生画、量等操作之后，通过反馈、对比，在学生规范演示画中落实“你是怎么找的”。

4.明确垂直线段，组织讨论：这条线段有什么特别吗？

（板书：垂直线段）

5.思考讨论：垂直线段一定是最短的吗？可以怎样验证？

通过测量验证，优化突出垂线在这些线中的地位。

小结指出：这条线段果然特殊，不仅垂直而且还是最短的。

（板书：垂直线段最短）

【设计意图：通过学生自主探究、规范、修正，了解垂直线段最短，特别是要区别于以往学生认知当中的“竖直最短”这一认识，规范距离的画法。】

6.引出概念：引导学生解读概念，并且明确点O到m的距离就是线段OM的长度。

7.跟进练习：出示图片。

（1）辨析：以下三位同学谁说得对？为什么？

A同学：AF就是点A到直线n的距离。

B同学：AH、AF、AE都可以看作A到直线n的距离，只是长短不一。

C同学：不对，点A到直线n的距离应该是垂直线段的长度，这里没有垂直线段。

（2）找出正确的距离。

说一说什么叫点到直线的距离？如果想知道直线外一点到直线的距离是多少应该怎么做？

（板书：一画，二量）

【设计意图：通过概念辨析，帮助学生进一步明确“点到直线的距离”的核心要素在于“垂直线段”、“长度”，在此基础上梳理小结得到距离的步骤方法。】

三、自主探究，提升距离本质

跟进情境：慢羊羊路的设计图。要求：这条路要设计通过5米宽的车子，下面的设计图可行吗？（图上1厘米表示1米）

1.自主探究：在直线a上任意找几点，并表示出两平行线之间的距离，量一量。

2.展示交流，小结指出：平行线间的距离处处相等。

【设计意图：通过检验路宽是否符合要求这一生活问题，激发了学生对平行线之间距离性质的探究欲望，提供了较为开放的自主探究空间。】

四、理解应用，夯实距离本质

1.图形中的距离。

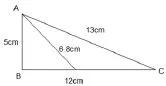
点A到线段BC的距离是（ ）厘米，点C到线段（ ）的距离是12厘米。

2.填一填

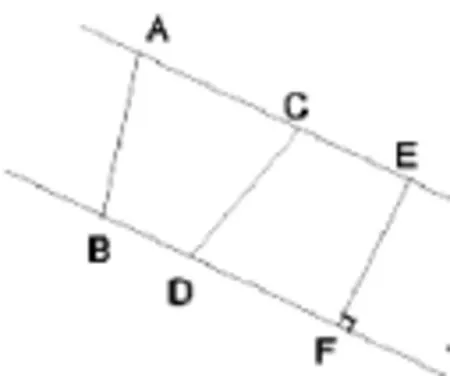
已知平行线之间的距离是3厘米，线段（ ）的长度是3厘米。

3.生活中的距离。

出示三幅生活中的距离问题图：

（1）跳远比赛中如何测量成绩？结合学生描述，在生活情境图片中用数学方式抽象出“脚后跟到踏板的距离”。

（2）怎样用最快的速度通过斑马线？顺着学生的描述和动作，用做垂直线段的方式呈现出最短距离。

（3）怎样挂画又快又正？放手讨论的同时，点名学生回答，追问：结合今天所学的知识来完整的说一说

【课后回望】

一、依托情境，激发生活经验，助力理解“距离”的概念

本设计创设了多处情境让学生去感悟、理解“点到直线的距离”这个概念。比如，围绕帮助慢羊羊村长设计一条从羊村到公路的小路为主问题展开，学生结合生活经验触发对要修一条最短的路的需求，并以此为切入口对最短问题展开主动研究。又如，在学习“平行线之间的距离处处相等”这个知识点时，笔者设计了“能通过5米宽的路吗？”现实问题情境让学生去思考、研究。通过问题情境，有效激发了学生的经验和兴趣，为概念的过程性学习提供较好保障。另外，在练习环节安排了“跳远成绩如何测量？过斑马线怎样最快？如何把画摆正？”等生活化练习，促进了学生对概念的理解与应用。

二、变式引入，打破思维定势，凸显“距离”概念的本质

在情境创设的同时，笔者并没有只停留于问题表象，而是深度挖掘了知识本质展开教学。在设计中笔者对主例题进行了改变，为了不让学生混淆“竖直线段就是垂直线段”这一概念，将公路斜着出示，当然也是为了能更快地触及垂直线段的本质，迫使学生寻找“垂直”这一抓手。在点到直线的距离认识中，围绕“找无数条线段——最短线段——垂直线段最短——垂直线段的长度是距离（以及对距离概念的辨析）”的路径，通过层层递进的操作、判断、辨析等活动，始终围绕着距离的核心要素展开教学，帮助学生理解和掌握距离概念的本质。