基于球管模型核磁共振T2谱反演新方法
王飞飞, 章海宁, 汤天知, 刘堂宴
(1.海洋地质国家重点实验室(同济大学), 上海 200092; 2.中国石油集团测井有限公司, 陕西 西安 710077)
0 引 言
核磁共振T2谱提供的岩石物性和流体特性的信息如岩石孔隙大小分布、有效孔隙度、渗透率、可动流体与不可动流体饱和度等为地质勘探和油田开发过程中的储层评价、产量预测和开发方法的制定提供了重要依据[1-2]。核磁共振测井原始回波串数据通过多指数反演获得用于地层评价的T2谱。Butler等[3]讨论了罚函数法(BRD),Dunn等[4]讨论了非负最小二乘曲率平滑法,王为民等[5-6]讨论了奇异值分解(SVD)法,翁爱华等[7]研究了核磁共振测井数据高分辨率反演方法,王忠东等[8]讨论了联合迭代重建算法(SIRT),陈华等[9]将差分进化算法(DE)引入到核磁共振弛豫信号反演。其中,以SVD算法为一般应用算法。本文考虑孔隙结构,在球管模型的基础上,优化常规的对数均匀布点方式,进而优化了核矩阵,并基于Tikhonov正则化思想,实现了SVD反演算法和共轭梯度CG算法的改进。
1 核磁共振多指数弛豫模型
核磁共振扩散理论表明,单个孔隙内磁化强化信号的横向弛豫具有单指数衰减规律。岩石内部孔隙介质是一系列大小不等的孔隙群组成,所测量的总磁化强度信号是一系列指数衰减信号的迭加,其计算模型为
d1=f1e-t1/T2,1+f2e-t1/T2,2+…+fne-t1/T2,n
d2=f1e-t2/T2,1+f2e-t2/T2,2+…+fne-t2/T2,n
⋮ ⋮ ⋮ ⋮
dm=f1e-tm/T2,1+f2e-tm/T2,2+…+fne-tm/T2,n
(1)
式中,m,n分别为回波个数和弛豫分量个数(布点个数),m>n;ti(i=1,2,…,m)为第i个回波采集时间,是回波间隔(TE)的整数倍;fj(j=1,2,…,n)为第j个弛豫分量的初始幅度,经过刻度,可以表示为第j种孔隙占总孔隙的百分比;di为第i个回波的幅度;T2j为横向弛豫时间常数。矩阵形式
Ym×1=Am×nfn×1
(2)
通常,m>n,而且核矩阵A的条件数非常大,因此,该方程是个病态问题。另外,物理意义上fj≥0即方程(2)还应该满足非负条件。
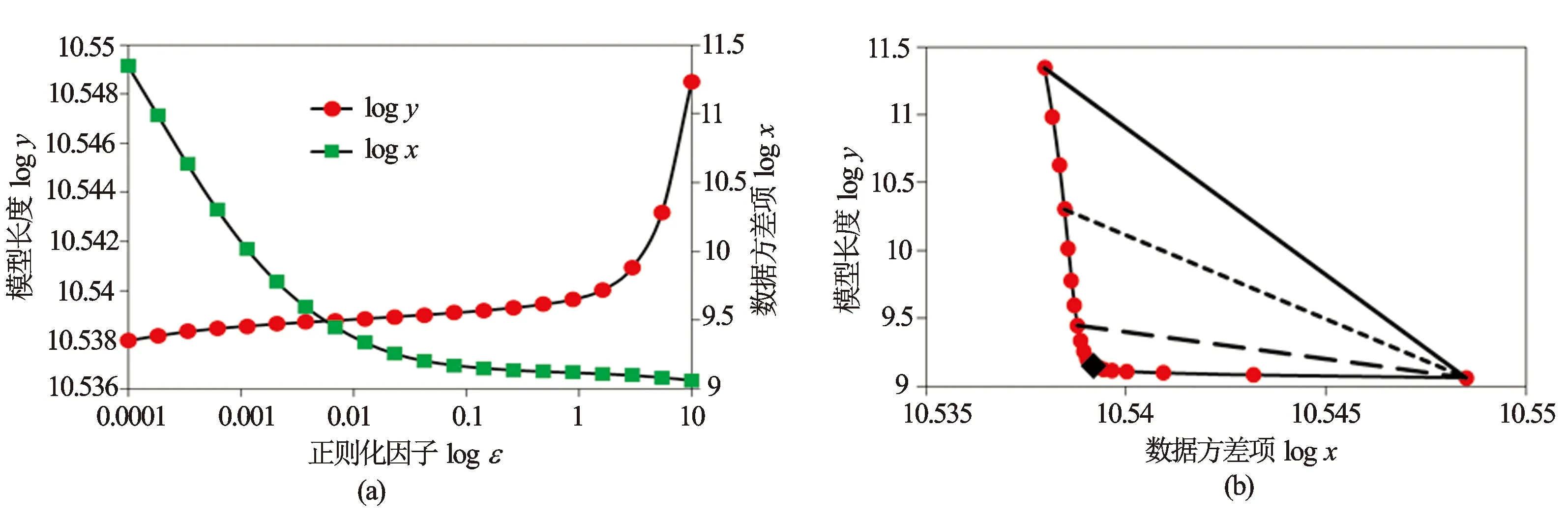
图1 x和y与ε的关系曲线(a)及典型的L曲线图(b)
1.1 Tikhonov截断奇异值法(TTSVD)
Tikhonov正则化方法是解决病态问题应用最为普遍的方法[10-11],其估算准则为
OF=‖Af-d‖2+ε‖Lf‖2=min
(3)
式中,ε为正则化因子,控制残差和解的约束大小的权重;这里L取单位矩阵,对应零阶正则化。该目标函数兼有数据方差项和模型长度项2项内容,为了使得目标函数达到最小,对f求偏导数,并令其为0,得到正则化解
freg=(ATA+εI)-1ATd
(4)
大多数地球物理反演问题,ε为0或足够大都难以取得模型的最优解,有必要寻找一种折中方案。其中,L曲线法是一种很好的确定正则化因子的方法。
L曲线法的基本思想是对于不同的正则化因子在双对数坐标下数据方差项和模型长度项之间的关系曲线呈现出“L”形,其拐角处所对应的正则化因子即是所要选择的最佳正则化因子。
对于连续的L曲线,可以通过求取L曲线的曲率,曲率最大点所对应的正则化因子即为所求。
(5)
显然,x和y都是正则化因子的函数。通常x与ε呈现递减关系,y与ε呈现递增关系[见图1(a)]。曲率k可以表示为
(6)
实际过程中,L曲线并不连续。一般做法是通过预先给定一系列正则化因子ε,可以得到对应的x和y,在双对数坐标下绘出两者的关系曲线。这种情况下可以构造一系列的三角形,最大面积(也可以理解为L曲线上的点到起始点连线段距离最大)所对应的正则化因子即为最佳的正则化因子[见图1(b)]。
不考虑正则化因子,则正则化解为最小二乘(LS)解
fLS=(ATA)-1ATd
(7)
对核矩阵A进行SVD分解
(8)
式中,U和V满足
UTU=VTV=In
(9)
则最小二乘解的奇异值分解形式为
(10)
奇异值λi减小得非常快,当i值很大时,对应的奇异值λi很小,此时即是观测数据中含有较小的误差都将使得最小二乘解较大地偏离真实值。实际测量的回波数据中包含有噪音,为了避免上述现象,通过设置一个阈值,将奇异值中小于阈值的赋值为0,即可消除小的奇异值对最小二乘解得影响,达到消除方程病态性的目的。应该注意到,去除的奇异值越多,损失的有用信息也越多。因此,有必要寻找一个合理的阈值,既能保证病态方程得意消除,又能保留足够多的有用信息。
关于奇异值截断,王为民等[5]提出利用信噪比进行截断的方法
(11)
林峰等[12]通过分析最佳奇异值保留个数与信噪比的关系,提出了改进的奇异值截断算法,并且提出,在回波个数m=500、布点个数n=30的条件下可以取a=1.45,b=16,有
(12)
这里,信噪比SNR的定义方式为
(13)
非负约束方面,姜瑞忠等[13]从向量空间的角度对SVD算法进行了分析,提出了一种新的实现非负约束的迭代方案。
由此,TTSVD反演算法可以概述为2步:L曲线法确定正则化因子,得到正则化解作为初始模型;TSVD迭代,加入非负约束条件。
1.2 共轭梯度法(CG)
CG法是由Hesteness和Stiefel于1952年为求解线性方程组而提出的,是解决大型线性和非线性方程组的最优化有效的算法之一,其基本思想是把共轭性与最速下降法相结合,利用已知点处的梯度构造一组共轭方向,并沿着此组方向进行搜索,求出目标函数的极小点。CG的算法流程如下。
(1) 初始化:初值x0∈Rn,计算残差r0=b-Ax0和d0=ATr0,给定最大迭代次数和算法终止常数err>0;置k=0,开始迭代;
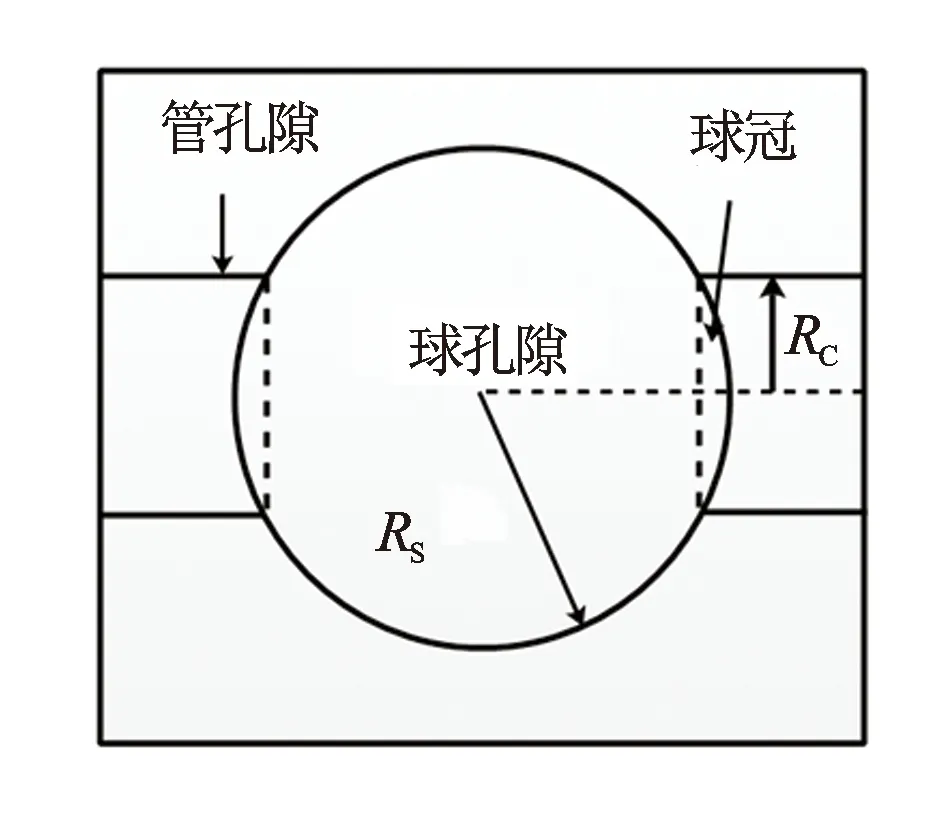
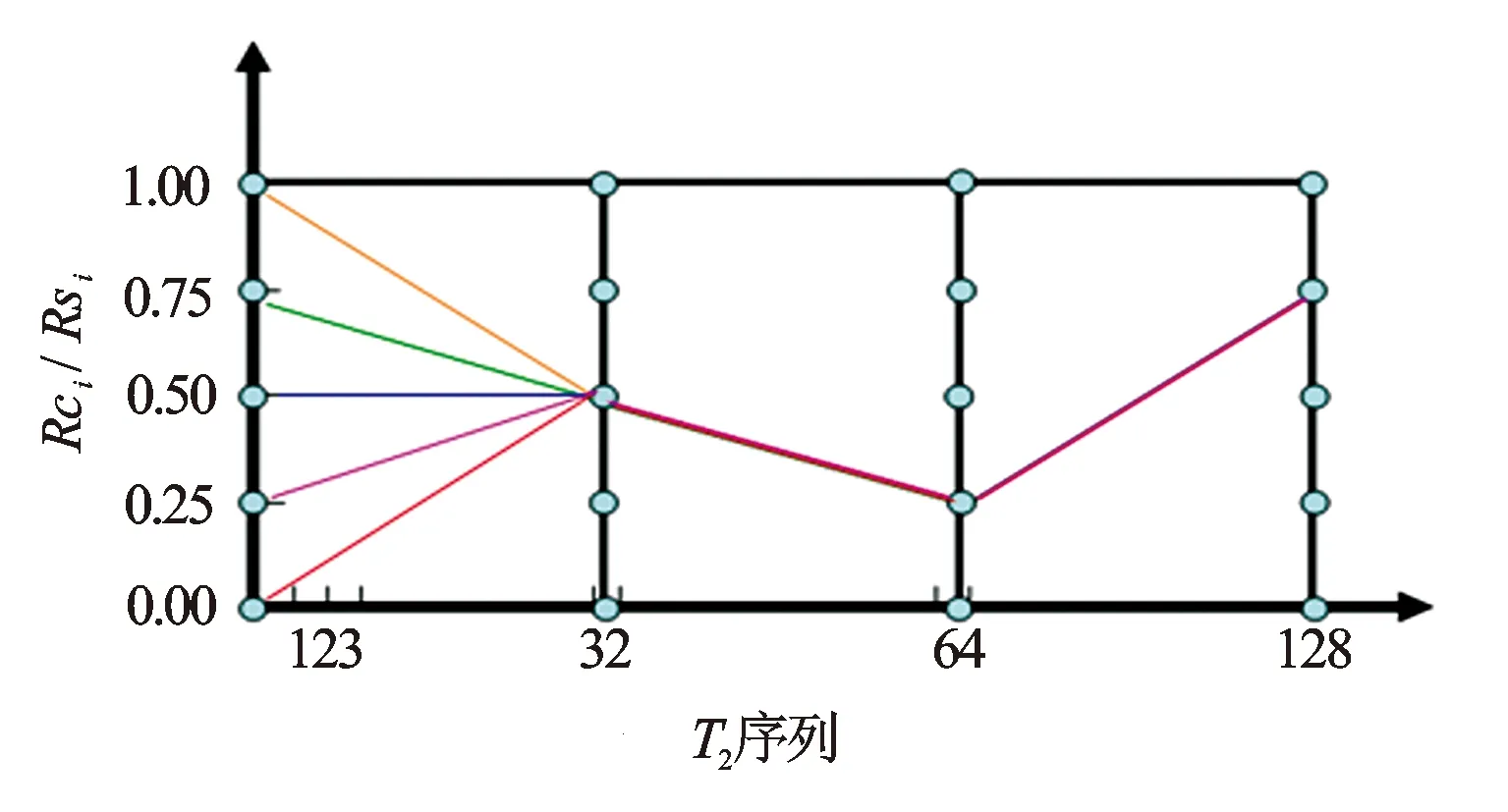
(2) 若‖rk‖ (4) 计算:βk=‖ATrk‖2/‖Ark-1‖2,dk=ATrk+βkdk-1; k=k+1,回到(2)。 球管模型[14]考虑了球孔隙和管孔隙在不同组合形式下具有的核磁共振特征,其基本思路是根据预先的布点方式确定各孔隙组分的等效球半径Re,通过预先设定的不同球管配比关系(引入“路径”概念),加上表面积约束条件,可以确定新的布点方式,利用新的布点方式优化核矩阵进行反演,对比回波拟合曲线,找出拟合方差最小的一组路径,即得到岩石最可能的理想孔隙结构。 球管模型(见图2)的描述方程 (14) 式中,S、V和R分别为面积、体积和半径,下标s、c为球孔隙和管孔隙。 图2 球管模型平面示意图 表面积约束条件 (15) 求解上述方程得到优化的布点方式 (16) 理论上,预先设定的路径有无数条,每一个布点处都可能对应着不同大小的球管模型,即不同的Cd(管半径与球半径比值)值(见图3)。为了方便计算,简化了路径数量,给出了8种比较典型的路径形式,用优化的路径处理实际数据,速度大大提高。球管模型的思想可以概括为,将各岩石孔隙网络等效为一系列不同大小的球孔隙和管孔隙,对应不同Cd值的球管模型,扫描所有路径并择优,选择相对最佳路径和最优解。 图3 球管模型路径扫描 图4 正演双峰模型与回波衰减曲线 构造一个典型的双峰谱模型,布点时间0.3~3 000 ms,布点个数为30,回波时间为0.9 ms,回波个数500[见图4(a)]。对正演的回波[见图4(b)]加入不同比例的噪音,信噪比定义为第1个回波幅度与噪音(模型回波衰减曲线与回波拟合曲线之差)方差之比,即 (17) 正演结果表明,不同程度的噪音影响,CG和TTSVD的2种方法都能反演出模型谱的双峰结构(见图5)。噪音水平为5%,2种方法反演谱与模型谱差别不显著;噪声水平低于1%,2种方法反演的谱与模型谱几乎完全重合。总之,2种方法都能提供较好的反演结果。TTSVD的反演结果略优于CG法,但反演所需的时间比CG多。 图5 CG与TTSVD正演结果图 用这种优化核矩阵的方法反演了不同地区共45块岩心样品。其中,除个别岩样属中孔隙度(介于15%~25%)外,其余都属于低孔隙度(介于10%~15%),大部分属于特低孔隙度(小于10%)。 图6 岩心反演结果对比 从图6可知,实验室给的反演结果大部分都在1个孔隙度误差范围内,改进的奇异值分解方法(TTSVD)反演结果都在1个孔隙度误差范围内,共轭梯度法(CG)反演结果除个别点结果都在1个孔隙度误差范围内。2种方法反演结果都优于实验室给的结果。图7是相对误差情况,实验室结果相对误差大部分都在5%以上,平均为7.43%,2种方法的相对误差大部分都在5%以内,平均TTSVD为3.93%、CG为3.54%。特别如黑框所示,岩样属特低孔隙度,相对误差都在10%以上,最高可达18%;该方法尤其是CG法基本都在10%以内。从T2谱形态上看,对于单峰形态,2种方法和实验室结果几乎一致;对于实验室给出的不明显的双峰形态,2种方法都能给出明显的双峰形态(见图8)。 图7 岩心反演误差分析 图8 2块岩样的反演T2谱对比 将2种优化反演方法用C语言编制成相应的计算机程序,依托CIFlog测井解释平台,实现对实际核磁共振测井数据的反演(见图9),2种方法反演的结果基本类似,无明显差别,仅在T2谱形态和幅度上略微有不同。 图9 实际核磁共振测井数据反演实例 (1) 考虑Tikhonov正则化,提供初始模型;使用截断奇异值分解进行非负约束迭代,得到最终解,正演模型效果很好。 (2) 共轭梯度算法在T2谱反演中有很好的应用。 (3) 以球管模型为基础,优化T2弛豫时间布点方式,改进核矩阵,进而优化T2谱反演,对比本文方法反演谱和实验室反演谱有很大程度上的相似性,并且对T2谱的多峰形态有更好的反映。孔隙度计算结果,该方法结果与气测孔隙度更加接近,说明该算法具有很好的实用性,可以用于岩心核磁共振T2谱反演,尤其是对于低孔隙度甚至特低孔隙度岩心有很好的应用效果。 (4) 依托CIFlog测井解释平台,实现了实际核磁共振测井数据的反演。 (5) 考虑孔隙结构的核磁共振T2谱反演方法可以作为计算孔隙结构参数如分选系数、歪度、峰度、中值半径等的基础。 参考文献: [1] Kenyon W E. Petrophysical Principles of Applications of NMR Logging [J]. Log Analyst, 1997, 38: 21-43. [2] Timur A. Producible Porosity and Permeability of Sandstones Investigated Through Nuclear Magnetic Resonance Principles [J]. The Log Analyst, 1969, 10(1): 3-11. [3] Butler J P, Reeds J A, Dawson S V. Estimating Solutions of First Kind Integral Equations with Nonnegative Constraints and Optimal Smoothing [J]. SIAM Journal on Numerical Analysis, 1981, 18(3): 381-397. [4] Dunn K J, LaTorraca G A, Warner J L, et al. On the Calculation and Interpretation of NMR Relaxation Time Distributions [J]. SPE Paper, 1994, 28369. [5] 王为民, 李培. 核磁共振弛豫信号的多指数以演 [J]. 中国科学: A辑, 2001, 31(8): 730-736. [6] 李鹏举, 葛成, 孙国平, 等. 基于奇异值分解的核磁共振测井T2谱反演方法的改进 [J]. 测井技术, 2010, 34(3): 215-218. [7] 翁爱华, 李舟波, 莫修文, 等. 核磁共振测井数据高分辨率反演方法研究 [J]. 测井技术, 2002, 26(6): 455-459. [8] 王忠东, 肖立志, 刘堂宴. 核磁共振弛豫信号多指数反演新方法及其应用 [J]. 中国科学: G辑, 2003, 33(4): 323-332. [9] 陈华, 潘克家, 谭永基. 核磁共振弛豫信号多指数反演新方法 [J]. 测井技术, 2009, 33(1): 37-41. [10] Hansen P C, O’Leary D P. The Use of the L-curve in the Regularization of Discrete Ill-posed Problems [J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487-1503. [11] Hansen P C. Analysis of Discrete Ill-posed Problems by Means of the L-curve [J]. SIAM review, 1992, 34(4): 561-580. [12] 林峰, 王祝文, 刘菁华, 等. 核磁共振T2谱奇异值反演改进算法 [J]. 吉林大学学报: 地球科学版, 2009, 39(6): 1150-1155. [13] 姜瑞忠, 姚彦平, 苗盛, 等. 核磁共振T2谱奇异值分解反演改进算法 [J]. 石油学报, 2006, 26(6): 57-59. [14] 刘堂晏, 周灿灿, 马在田, 等. 球管孔隙模型的约束寻优及应用 [J]. 同济大学学报: 自然科学版, 2006, 34(11): 1464-1469.1.3 球管模型约束优化反演
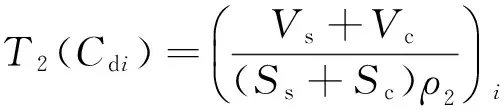
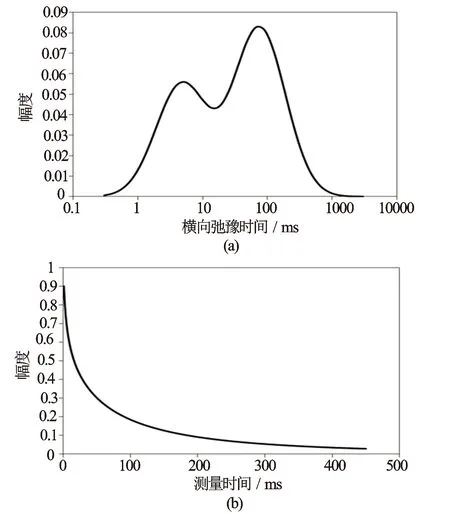
2 正演数值模拟
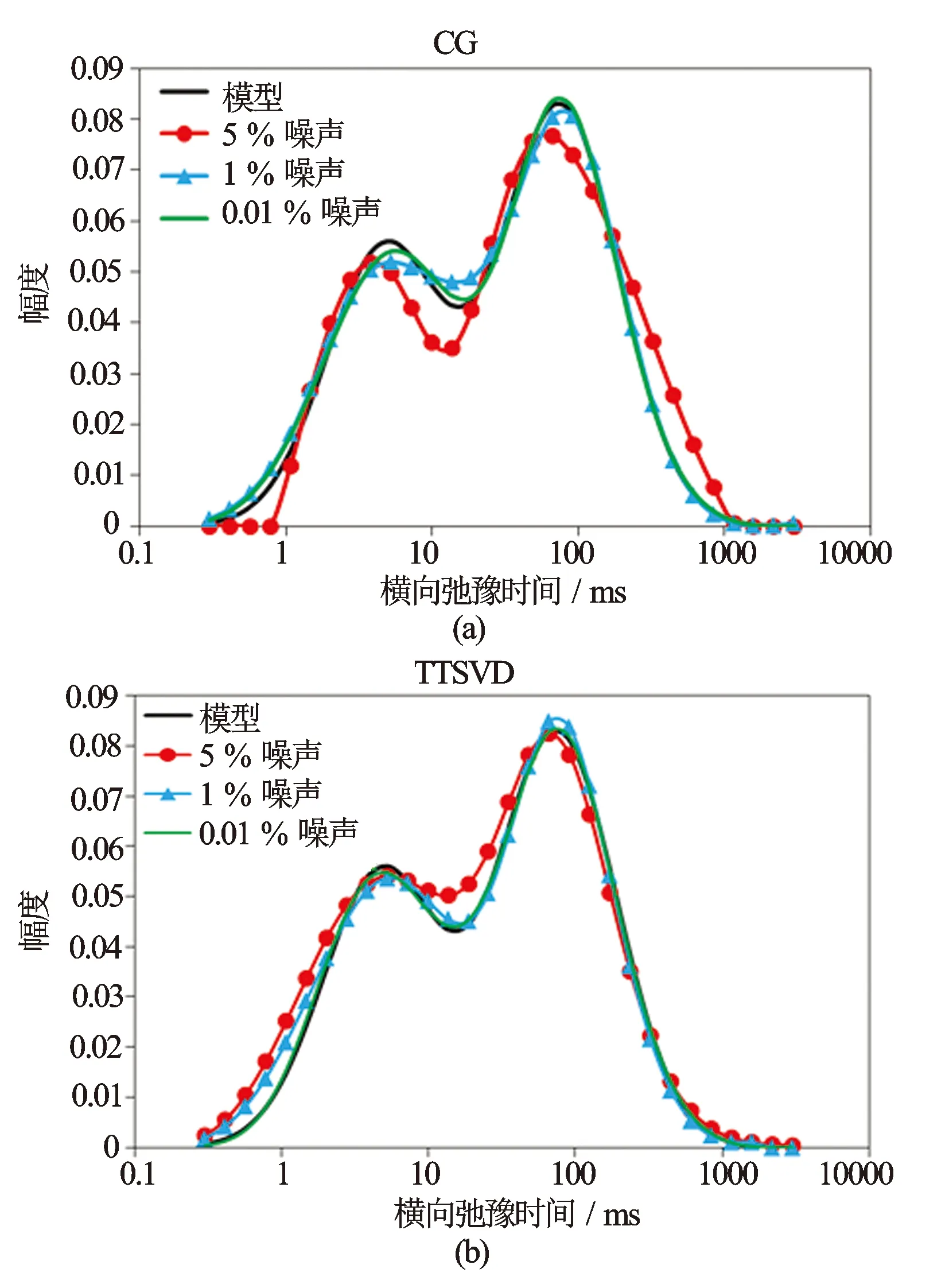
3 实际岩心检验与核磁共振测井资料处理
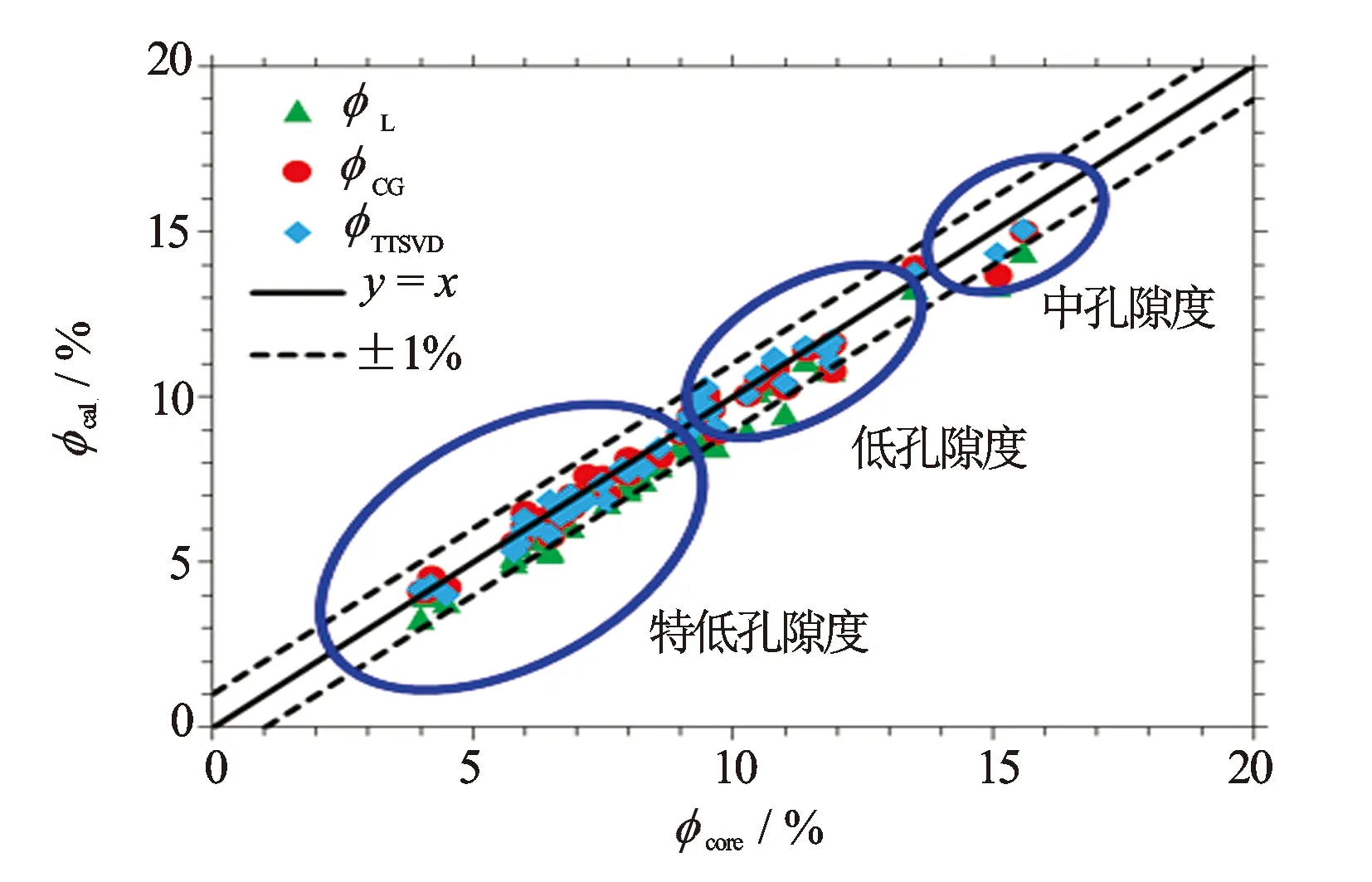
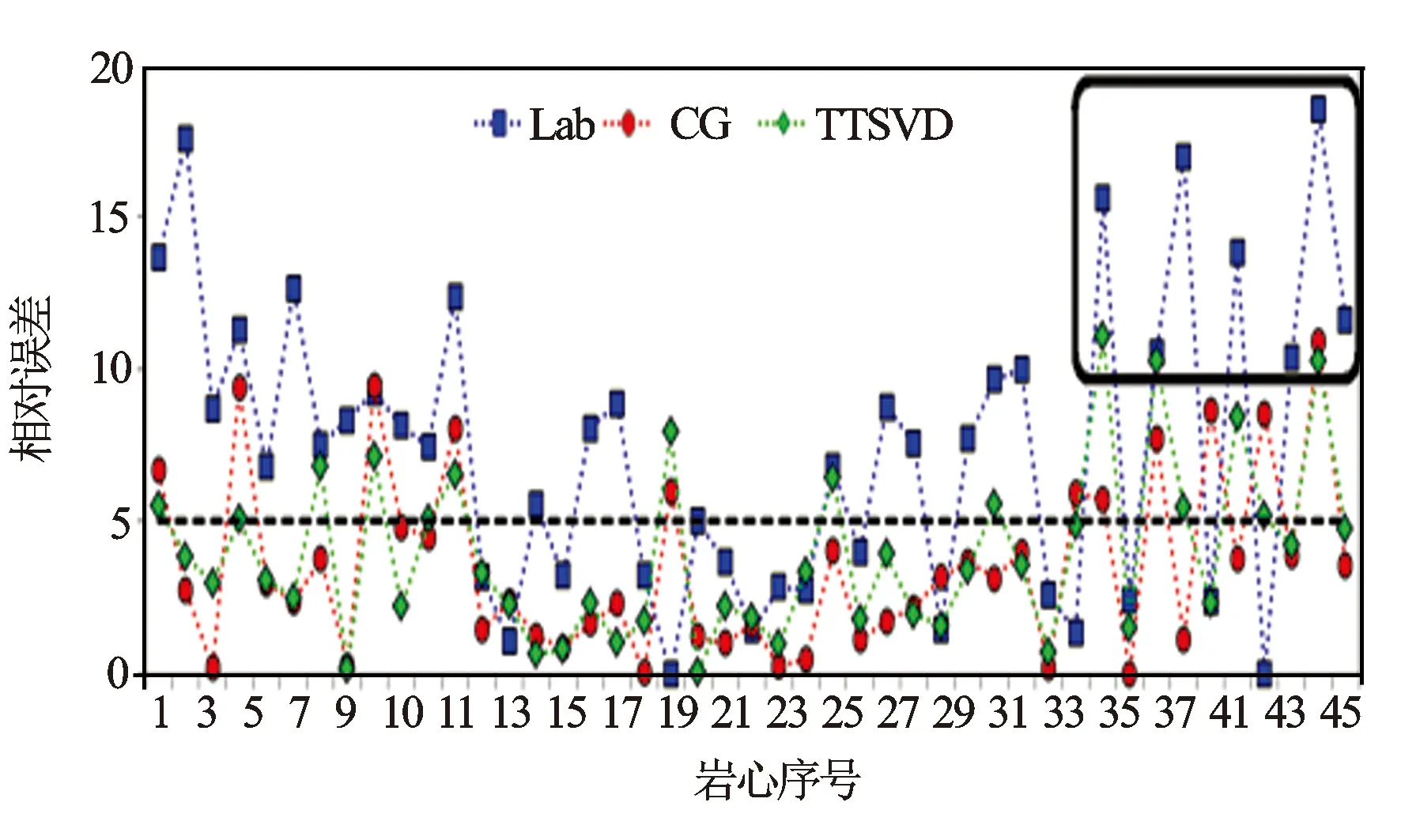

4 结 论

