基于科氏质量流量计的两相流计量方法研究
王微微, 陈静静, 孙峰超
(1.中国石油大学(华东)信息与控制工程学院, 山东 青岛 266580;2.中国航空油料有限责任公司, 山东 淄博 255434)
0 引 言
石油石化气、液两相在流动过程中相互作用,分相流量的检测难度很大[1-2]。大多油田采用分离计量法计量原油的分相流量。这种方法气液分离效果较差,往往在液相中混有一定量的气体;混有的气体对液相流量的计量精度有很大影响,也影响气体流量的准确测量。气液两相流的动态特性比较复杂,导致气液两相流流量的准确计量存在很大难度[3-4]。科氏流量计能够精确测量单相流体的质量流量,在测量气液两相流时不准确,产生较大的测量误差,在很大程度上限制了科氏流量计在石油等行业中的应用。国内外很多专家学者对此进行了研究,但科氏流量计测量气液两相介质参数时误差仍然较大,中国还没有成熟的应用于两相流参数计量的流量计[5-11]。本文利用黏性流体气泡模型对科氏流量计测得的质量流量和密度进行修正,以减小科氏流量计测量气液两相流的误差。
1 实验装置
实验在中国石油大学(华东)多相流试验平台上进行。实验介质为水、压缩空气。实验装置如图1所示。1号质量流量计为高准100M329型科氏流量计,气体流量计为孔板流量计;2号(科氏)质量流量计计量不同含气率下气液两相流的质量流量、密度等参数。实验中,液相流量3.5~16 m3/h,气相流量0.07~2.5 m3/h,表压0.25~0.4 MPa。
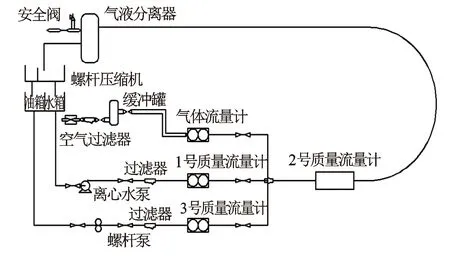
图1 油气水三相流实验平台简图

图2 气液两相流经科氏传感器示意图
在实验介质供应系统中,水由泵泵送,经调节阀调压后,经1号质量流量计计量后送入混合器。单相气体经空气压缩机压缩,再经调节阀调压后,经气体流量计计量后送入混合器。气体流量计为不同口径的孔板流量计,针对不同实验工况采用不同口径孔板流量计计量气体流量。气液两相经混合器均匀混合后,沿一段长约354 m,直径约81 mm的管道流动,达到稳定状态,然后进入实验环道测试。实验装置设置了末点处理系统,以测量流体是否进入稳定状态。在实验环道,由2号质量流量计计量气液两相流瞬时质量流量、混合密度和温度。在实验环道内,环道水平安装,2号科氏质量流量计垂直于环道安装。最后,气液两相流经气液分离器分离,气体排空,水返回水箱。
图2为气液两相流混合液流经科氏传感器的示意图。在图2中,驱动装置使科氏力传感器测量管以固定频率进行振动。测量管的两侧有检测线圈及其磁铁构成的左右检测器。当测量管中有介质流动时,检测器检测到流动与振动耦合作用导致的附加位移,此附加位移与测量管中介质的质量流量有关,因此可通过测量此附加位移计算测量管中介质的质量流量。当含气介质在测量管中流动时,测得的质量流量瞬时变化。
2 气泡模型
Hemp等[12]提出了黏性流体的气泡模型,该模型综合考虑气相速度和流体黏性,指出:
(1) 对于黏度为0的流体质量流量测量误差为
Em=-2α/(1-α)
(1)
(2) 对于高黏度的流体或有细小气泡的流体,质量流量测量误差为0。
由黏性流体的气泡模型可知,当流体黏度大于0且黏度不高时,质量流量的相对误差可表示为
Em=K[-2α/(1-α)]
(2)
式中,K为修正系数。
3 实验结果分析
在大部分两相流工况下,气相的存在使得科氏流量计不能准确测量液相质量流量。本文对质量流量计测得的混合密度进行修正,再结合两相流的含气率,根据气泡模型对测得的质量流量进行修正。
气液两相流混合密度为
ρ=(ρg-ρl)α+ρl
(3)
式中,ρl为液体密度,g/cm3;ρg为气体密度,g/cm3;α为空隙率,小数,无量纲。
由式(3)可以推出
α=(ρ-ρl)/(ρg-ρl)
(4)
令密度降Δρ为
Δρ=(ρl-ρ)/ρl=α(ρl-ρg)/ρl
(5)
可见,密度降Δρ与空隙率α密切相关。
定义两相流体的示值密度降Δρapp和真实密度降Δρt分别为
Δρapp=(ρl-ρapp)/ρl
(6)
Δρt=(ρl-ρt)/ρl
(7)
其中,真实密度值ρt由ρl、ρg和α确定。实验中,ρt由快关阀法确定。
如图3所示,根据实验数据,真实密度降Δρt与流量计视密度降Δρapp关系为
Δρt=1.0989Δρapp+0.0171
(8)
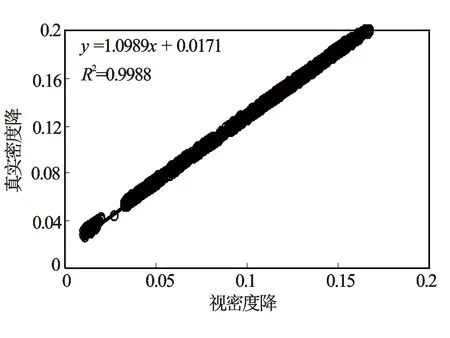
图3 真实密度降与视密度降关系图
根据式(6)、式(7)和式(8)可推导出修正后两相流的密度ρt
ρt=ρl-Δρt·ρl
(9)
密度测量相对误差计算式为
Edens=(ρ-ρt)/ρt
(10)
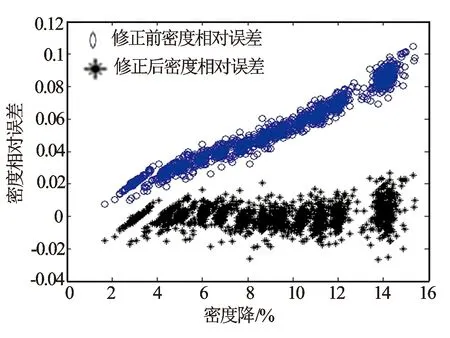
图4 空气-水两相流密度测量相对误差
修正前后的两相流密度相对误差见图4。图4中,修正后气液两相混合流体的密度相对误差明显变小,且保持在2%以内;密度降小于6%的气液两相流基本为泡状流型,气体呈细小的泡沫状流动,且较均匀分布在测量管中,细小气泡的存在使得气液两相流的密度略小于液相密度。当泡状流态的两相流流经科氏传感器检测元件时,产生的力矩偏小,传感器左右检测信号的相位差也偏小,导致科氏质量流量计的质量流量和密度测量出现误差。但由于气泡较小且分布均匀,因此该误差较小。当密度降大于6%时,出现较大的非均匀分布的大气泡,当密度降大于10%时,出现段塞流型,气液两相流密度减小,此时,流体作用在传感器检测元件处的力矩变化较大,导致质量流量和密度测量出现较大误差。将测量密度修正为真实密度有助于改善质量流量的测量误差。
将修正的两相流密度代入式(4),得到当前的空隙率α。
最后,利用气泡模型对2号质量流量计测得的两相流质量流量进行修正。对空气-水两相流,取K=0.065,由此得到修正的质量流量为
(11)
式中,Fapparent为2号质量流量计测得的视流量,kg/min。
修正前后的气液两相流质量流量相对误差如图5所示。从图5可以看出,当空隙率较小时,修正效果较好,修正后的质量流量相对误差主要分布在2%以内;当空隙率较大时,修正效果较差。但在实验范围内,修正后的质量流量相对误差均好于修正前的相对误差。通过现场测量发现,当空隙率较高时,测量管激励信号仍能驱动测量管振动,但是振幅小,拾振信号小,噪声大,对测量结果的准确性有很大影响。
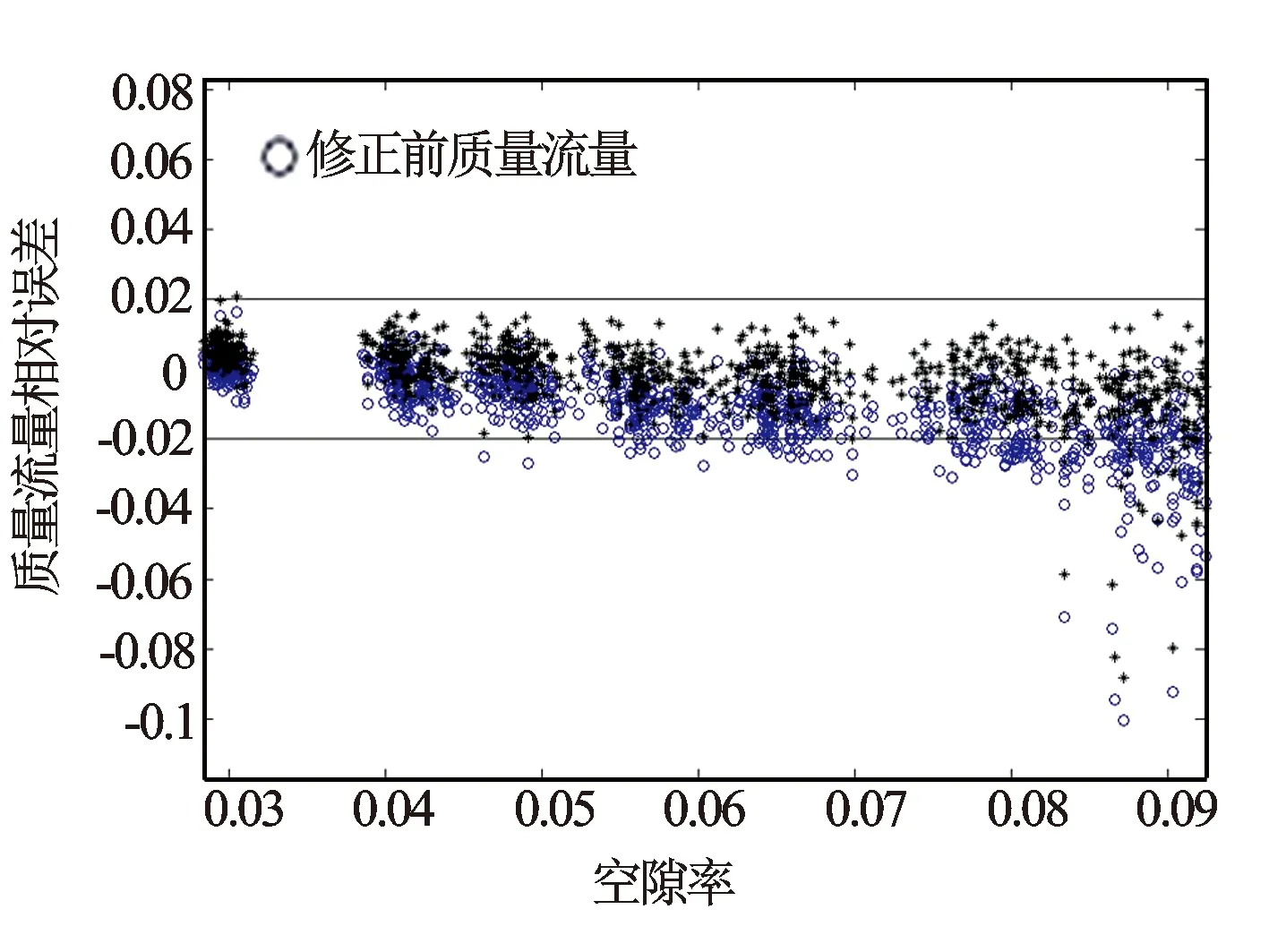
图5 空气-水两相流质量流量相对误差
4 结 论
(1) 利用黏性流体气泡模型对科氏流量计应用于气水两相流计量进行实验研究。泡状流态的两相流流经科氏传感器检测元件时,科氏质量流量计的质量流量和密度测量误差较小,段塞流型的气液两相流密度偏小,质量流量和密度测量出现较大误差。
(2) 修正后气液两相混合流体的密度相对误差明显变小,误差在2%以内。当空隙率较小时,修正后的质量流量相对误差主要分布在2%以内,修正效果较好。当空隙率较大时,科氏流量计测量管拾振信号小,噪声大,对测量结果的准确性有很大影响,修正效果较差。
(3) 在实验范围内,修正后的质量流量相对误差均好于修正前的相对误差。由于实验条件所限,本文密度修正关系适用的工况有限。
参考文献:
[1] 李海青. 两相流参数检测及应用 [M]. 杭州: 浙江大学出版社, 1991: 5-20.
[2] Hewitt G F. Measurement of Two Phase Flow Parameters [M]. London: Academic Press, 1978: 3-35.
[3] 陈家琅, 陈涛平. 石油气液两相管流 [M]. 北京: 石油工业出版社, 2010: 7-15.
[4] 李士伦. 天然气工程 [M]. 北京: 石油工业出版社, 2008: 5-37.
[5] Henry M, Tombs M, Duta M, et al. Two-phase Flow Metering of Heavy Oil Using a Coriolis Mass Flowmeter: A Case Study [J]. Flow Measurement and Instrumentation, 2006, 17(6): 399-413.
[6] 李祥刚, 徐科军. 科氏质量流量管非线性幅值控制方法研究 [J]. 电子测量与仪器学报, 2009, 23(6): 82-87.
[7] Dyakowski T. Application of Electrical Capacitance Tomography for Imaging Industrial Processes [J]. Journal of Zhejiang University SCIENCE, 2005, 6A(12): 1374-1378.
[8] Seeger M. Coriolis Flow Measurement in Two-phase Flow [J]. Computing and Control Engineering, 2005, 16(3): 10-16.
[9] Henry M P, Clarke, D W, Archer N, et al. A Self-validating Digital Coriolis Mass Flowmeter: An Overview [J]. Control Engineering Practice, 2000, 8(5): 487-506.
[10] Liu R P, Fuent M J, Henry M P, et al. A Neural Network to Correct Mass Flow Errors Caused by Two Phase Flow in a Digital Coriolis Mass Flowmeter [J]. Flow Measurement and Instrumentation, 2001, 12(1): 53-63.
[11] Johnson M W, Farroll S. Development of a Turbine Meter for Two-phase Flow Measurement in Vertical Pipes [J]. Flow Measurement and Instrumentation, 1995, 6(4): 279-282.
[12] Hemp J, Yeung H, Kassi L. Coriolis Meter in Two Phase Conditions [J]. Computing and Control Engineering, 2003, 14(4): 36.

