应用流动能力指数评价砂砾岩储层有效性

刘文辉, 申波, 高勃胤, 赵景

(1.中国地质大学地球物理与空间信息学院, 湖北 武汉 430074; 2.中石化华北石油工程有限公司测井分公司, 河南 新乡 453700; 3.长江大学油气资源与勘探技术教育部重点实验室, 湖北武汉 430010; 4.长江大学地球物理与石油资源学院, 湖北 武汉 430010)

0 引 言

储层有效性评价研究是测井评价的重点和难点[1-4],也是直接影响储量计算结果与勘探开发整体决策的重要因素。储层有效性评价往往根据试油井段的产能条件,通过化验资料、常规测井以及特殊测井资料的对比分析,确定储层有效性综合评价指标,进而建立研究区不同储层级别的分类标准。本文针对非均质性砂砾岩储层有效性评价,通过流动孔隙度理论的讨论和分析,从不同探测范围内流动能力差异入手,提出一种应用流动能力指数评价有效性的新方法。

1 流动孔隙度

1.1 理论背景

在测井解释中,地层电阻率因素定义为完全饱含地层水岩样的电阻率与地层水电阻率的比值(FR),即

(1)

式中,R0为完全饱含地层水岩样电阻率,Ω·m;Rw为地层水电阻率,Ω·m;a、m分别为岩性指数和胶结指数;φ为孔隙度。

Maxwell[5]发现,在连续的导电介质中,当分散、互相不接触的非导电介质为完全球体时,地层电阻率因素与孔隙度的关系可以表述为

FR=1+1.5(φ-1-1)

(2)

该方程建立的条件极具理想化,在测井解释中较少用到。Fricke[6]引入了几何形状参数的概念,假设非导电介质为椭球体,以Maxwell方程为基础,得到地层因素与孔隙度的关系表达式

FR=1+(1+x-1)(φ-1-1)

(3)

式中,x为几何形状参数,与椭球体长短轴比值有关。当x=2时,即等同于Maxwell方程,一般情况下,x<2。

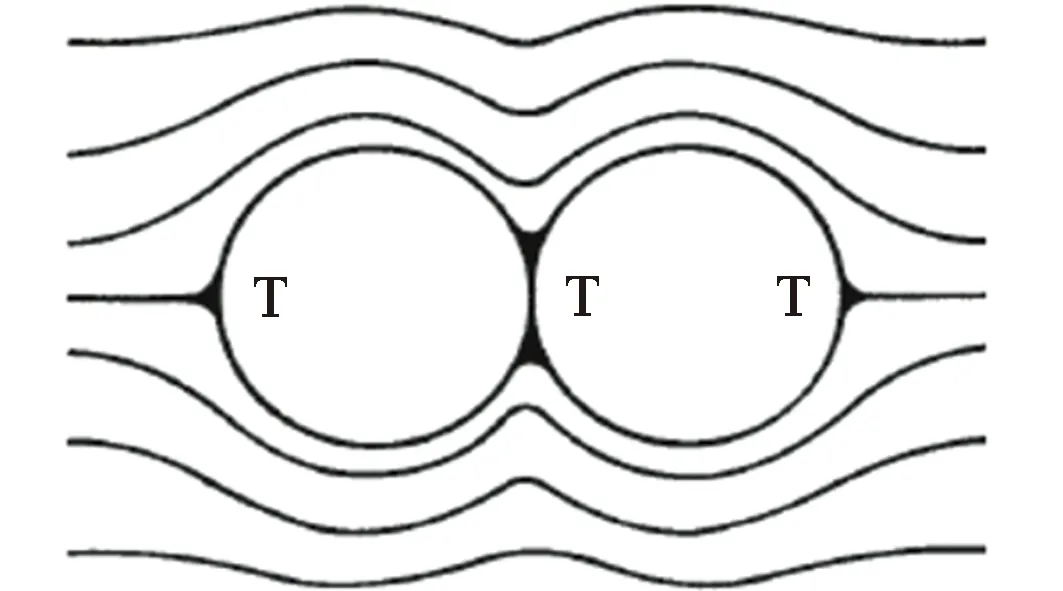
图1 Maxwell导电模型示意图[7]

当电流遇到非导电椭球体时(见图1),由于电流方向的突然改变,会在连续的导电介质空间范围内的某些区域形成电流“死角”(见图1中T处黑色标示区域代表无电流流动的孔隙空间),即除了非导电椭球体之外的流体空间内仍存在电流无法流动的区域。

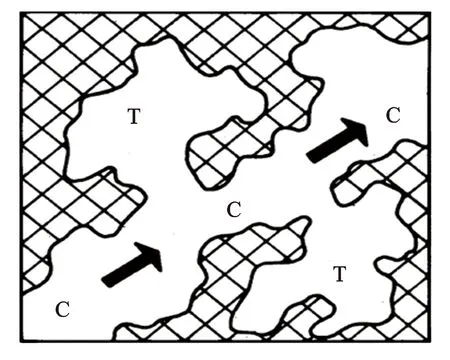
图2 孔隙介质平面示意图[8]

图2为孔隙介质平面示意图。由图2可知,即使在岩石完全饱含地层水条件时,由于岩石孔隙结构的复杂性,同样存在无电流流动区域(见图2中T处),实际电流流动通道为C所标示的区域。因此,根据电流的流动特性,可将总孔隙度分为流动孔隙度和静止孔隙度2部分,其关系表达式为

φ=φf+φs

(4)

式中,φf为流动孔隙度;φs为静止孔隙度。

1.2 计算方法

假设岩石骨架不导电,电阻率测井主要反映地层条件下岩石中连通孔隙内自由导电流体的信息。由于多种因素的耦合作用(井眼分流、导电矿物等),即使在无孔隙发育的致密地层中,电阻率也绝非无穷大。严格从电阻率测井值中分离出各种影响因素的电导率贡献值非常困难,实际应用中,通常岩石骨架的电导率可以采用常数或含水饱和度的函数代替[9]。

这里主要讨论一种简易的考虑岩石骨架导电条件下的流动孔隙度计算方法。首先定义除流动孔隙导电外的各种耦合作用电导率的总贡献值为背景电导率,用Cbg表示。在原状地层范围内,应该满足以下边界条件:当流动孔隙度等于0时,测井得到的电导率(Ct)为背景电导率(Cbg);当流动孔隙度等于1时,测量的电导率是孔隙流体电导率(Cf)。根据电导率线性叠加的性质,可得

(5)

式中,Ct、Cf和Cbg分别表示测井电导率、孔隙流体电导率和背景电导率。

根据Maxwell导电模型的分析可知,并不是所有含水孔隙空间内都存在自由流动的电流,即φw≠φf。因此,在油(气)、水共存条件下,孔隙流体的电导率取决于地层水电导率和电流能够自由流动的水体空间大小。因为油(气)不导电,所以有

(6)

式中,Swf为导电水饱和度;Cw为地层水电导率。

通过式(4)、式(5)和式(6)可知,当φf=0时,有φ=φs,即孔隙内无电流流动,测井电导率即为背景电导率;当φf=1时,有φ=φf=1,且φs=0,此时测量的电导率为地层水电导率。

为了区分连通孔隙空间和总孔隙空间[10],并降低理想条件下计算流动孔隙度的误差,式(6)改写为

(7)

式中,α为孔隙空间结构因子。

联立式(6)和式(7),经化简、合并可得

(8)

解式(8)关于φf一元二次方程,取其正值即为流动孔隙度值。

2 流动能力指数

钻井过程中,不可避免地会发生泥浆侵入渗透性储层的现象。泥浆滤液电阻率和地层水电阻率之间的差异,势必造成储集层电阻率在径向特征上的变化。在泥饼形成之前,这种渗流作用同时受到多种因素的制约,如孔隙度、渗透率、泥浆柱压力与地层压力差值、泥浆性能以及地层被钻开后经历的时间等。

流动孔隙度反映原状地层中导电水占据的孔隙空间。对于冲洗带地层,也可得到相应的流动孔隙度,其反映冲洗带地层范围内能够导电的泥浆滤液占据的孔隙空间。因此,根据式(8)可得其计算方程为

(9)

式中,Cmf、Cbgf、Cxo分别为泥浆滤液电导率,冲洗带背景电导率和冲洗带电导率;φff为冲洗带流动孔隙度,小数;αf冲洗带孔隙空间结构因子。

假设泥浆渗滤作用只与储层物性有关时,则储层物性越好,冲洗带内孔隙流体被泥浆滤液冲洗得越彻底,冲洗带流动孔隙度也就越接近总孔隙度,即φ-φff值越小;冲洗带流动孔隙度与原状地层流动孔隙度之间的差值也就越大,即φff-φf值越大。此外,泥浆的渗滤作用与岩性也有着密切的联系,因而需要引入岩性综合主成分F以反映泥浆渗流作用对不同岩性地层的差异程度[11]。为了消除综合主成分正、负值对计算结果的影响,对F值进行归一化处理,定义流动能力指数来衡量不同岩性储层泥浆渗流作用的大小,其表达式为

(10)

根据流动能力指数定义式可知,该参数是不同探测深度范围内的流动孔隙度差异及岩性的综合响应。由于储层厚度也是影响储层有效性评价的重要因素,因此,为了能够准确地衡量研究区储层的产出能力,按照单位厚度日产液量(该日产液量包括日产油、气和水,其中一方水按一吨产液量折算)的高低将储层分为3类。Ⅰ类储层:每米日产液量大于0.8 t;Ⅱ类储层:每米日产液量介于0.07～0.8 t;Ⅲ类储层:每米日产液量小于0.07 t。

利用该方法对某地区19口井50个试油层段进行了实际资料的处理,根据孔隙度—流动能力指数交会图建立了储层分类标准(见图3和表1)。

图3 研究区储层孔隙度—流动能力指数交会图

储层分类每米日产液量/t分类标准Ⅰ类储层>0.8ϕ>11%或IFC>0.8Ⅱ类储层0.07～0.87.5%≤ϕ≤11%时,IFC≤0.8;ϕ<7.5%时,0.4≤IFC≤0.8Ⅲ类储层<0.07ϕ<7.5%且IFC<0.4

3 应用实例

利用上述方法对研究区A井砂砾岩储层进行了实际资料的处理,同时结合孔隙度谱分析程序得到的不同孔径的孔隙度分布状态展开储层的有效性评价。

图4为A井2 268～2 300 m段流动能力指数及孔隙度谱处理效果图。根据孔隙度谱处理结果可以看出,次生孔隙主要发育于2 280～2 282 m井段和2 294～2 296 m井段,而试油层段2 266～2 273 m对应的孔隙度谱呈单峰分布特征,分布范围较窄,并且主峰靠近0孔隙度基线,表明该层段以原生孔隙为主,次生孔隙不发育;从FMI图像特征上看,该层段没有裂缝发育;另外,流动能力指数计算值小于0.4,试油验证为干层。从常规测井曲线响应特征上看,3个层段差异较小,但根据电阻率成像孔隙度谱和流动能力指数的分析能够较好的评价储层有效性。

图5为A井2 770 ～ 2 815 m段流动能力指数及孔隙度谱处理效果图。从整体上看,流动能力指数计算值明显大于干层,孔隙度谱分布范围较宽,且大都表现为双峰或多峰的分布特征,表明次生孔隙发育,并且孔隙分布尺度大,说明该层段非均质性较强,试油显示为高产油层。其中2 782～2 787 m井段流动能力指数平均值大于0.8,同时FMI图像特征显示裂缝非常发育。

图4 A井2 268～2 300 m段流动能力指数及孔隙度谱处理效果图*非法定计量单位,1 ft=12 in=0.304 8 m,下同

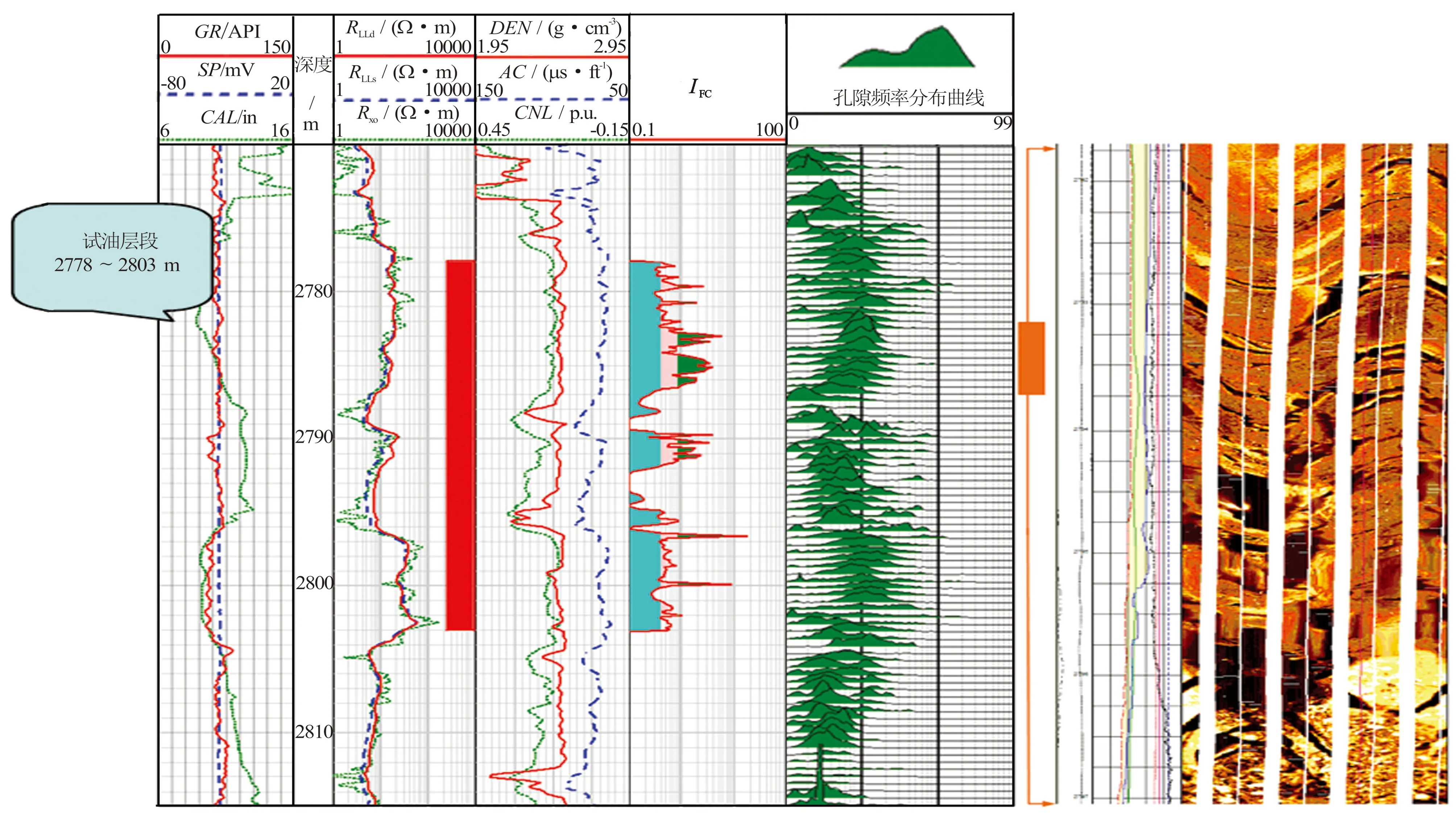
图5 A井2 770～2 815 m段流动能力指数及孔隙度谱处理效果图

4 结 论

(1) 在流动孔隙度理论分析的基础上,针对不同探测深度流动能力差异,提出了流动能力指数的概念,并建立了利用流动孔隙度和综合主成分计算流动能力指数的方法。

(2) 通过实际井资料的处理表明,利用流动能力指数能够较好的评价砂砾岩储层的有效性。在此基础上,根据孔隙度和流动能力指数交会的方法建立了研究区砂砾岩储层分类标准。

参考文献:

[1] 李全利, 吴春文. 基山砂岩体与盐家砂砾岩体储层特征分析与测井评价 [J]. 石油仪器, 2010, 24(2): 55-61.

[2] 李佳阳, 夏宁, 秦启荣. 成像测井评价致密碎屑岩储层的裂缝与含气性 [J]. 测井技术, 2007, 31(1): 17-20.

[3] 曾焱, 李涛, 叶素娟. 川西须家河组二段超致密储层有效性测井综合评价 [J]. 天然气工业, 2010, 30(6): 35-38.

[4] 司马立强, 姚军朋, 黄丹, 等. 合川气田须家河组低孔隙度低渗透率砂岩储层有效性测井评价 [J]. 测井技术, 2011, 35(3): 254-258.

[5] Maxwell J C. A Treatise on Electricity and Magnetism [M]. 3rd Edition. New York: Clarendon Press Republished by Dover Publications, Inc. , 1954.

[6] Fricke H. A Mathematical Treatment of the Electric Conductivity and Capacity of Disperse Systems [J]. Phys, 1924, 24: 575-587.

[7] Candelario P R. Generalization of the Maxwell Equation for Formation Resistivity Factors [J]. Journal of Petroleum Technology, 1976, 28(7): 819-824.

[8] Candelario P R. On the Relationship Between Formation Resistivity Factor and Porosity [J]. Society of Petroleum Engineers Journal, 1982, 9: 531-536.

[9] Worthington D F. Improved Quantification of Fit for Purpose Saturation Exponents [J]. SPE REE, 2004, 270.

[10] 张超谟, 张占松, 李军, 等. 基于港湾效应的导电机理与饱和度方程研究 [J]. 石油天然气学报, 2009, 31(6): 86-89.

[11] 申波, 毛志强, 樊海涛, 等. 基于主成分分析技术计算蚀变地层孔隙度的新方法 [J]. 测井技术, 2012, 36(2): 130-134.