速度矢量夹角可变的科氏加速度演示仪

王晓炜，章璐，王泽华，张棉好

（浙江师范大学工学院、职业技术教育学院，浙江 金华 321004）

0 引 言

对科里奥利加速度（简称“科氏加速度”）的分析，是《理论力学》和《机械原理》课程中的难点，主要是科氏加速度的产生原因和方向判断方法较难理解，而现有的演示仪只解决了水平式和立式两种特殊状态下的现象演示，不能演示倾斜方位下的现象演示和角度变化过程时的现象变化，从而学生较难理解速度矢量夹角变化对科氏加速度的影响。本文通过分析科氏加速度的产生原理，设计了一种速度矢量角度可变、可以在任意平面内演示科氏加速度的演示仪。

1 科氏加速度简介

当动系作定轴转动时，动点在某瞬时的绝对加速度等于该瞬时它的牵连加速度、相对加速度与科氏加速度的矢量和，而科氏加速度是由于动系为转动时，牵连运动与相对运动相互影响产生的。

科氏加速度是动参考系的转动与动点相对动参考系运动相互耦合引起的加速度,具体表达式为。式中，为科氏加速度矢量为牵连运动的角速度矢量为相对运动的速度矢量。

2 速度矢量夹角可变的科氏加速度演示仪

2.1 演示仪结构

图1 所示的速度矢量夹角可变的科氏加速度演示仪主要由牵连运动组件、相对运动组件组成，其中牵连运动组件由变频电机、同步带轮、机架、连接器、轴承、轴承架和大转盘组成，相对运动组件由支撑架、推杆电机、直流电机、演示台、演示轮和演示带组成。本演示仪通过推杆电机调节演示台角度，从而使牵连运动的角速度方向与相对运动的速度方向的夹角变化。

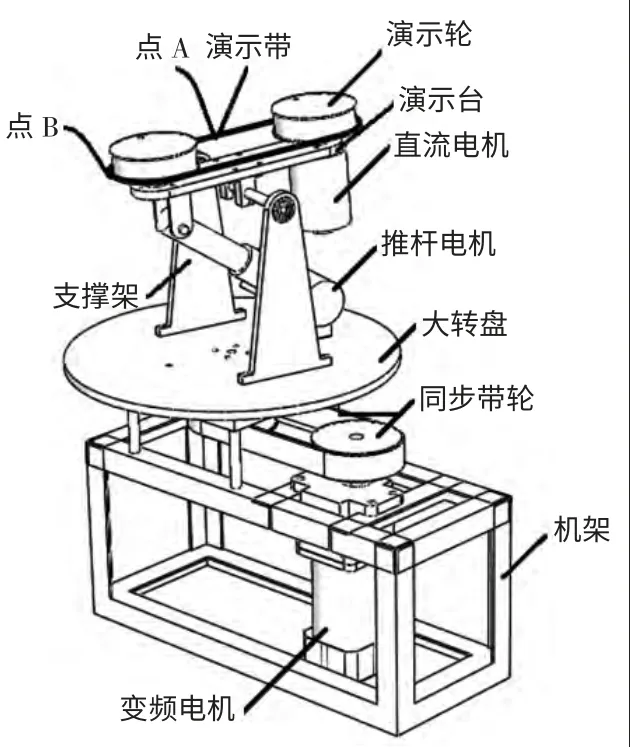
图1 速度矢量夹角可变的科氏加速度演示仪

2.2 演示仪原理及现象

2）当大转盘、演示带同时运动时，由于动参考系的转动和动点在动坐标系上的相对运动耦合，即产生科氏加速度：a.在水平状态下，观察点A（如图1 所示），点A 处矢量夹角θA＝90°，所以表达式可简化为。根据上式，演示带上点A 处产生内缩或外扩现象（具体现象由的方向决定）；

b.在垂直状态下，观察点B（如图1 所示），点B 处矢量夹角θB=90°，所以表达式可简化为。根据上式，演示带上点B 处产生向内移或向外移现象（具体现象由的方向决定）；

c.在倾斜状态下，观察点A 和点B（图1），矢量夹角θ处于0°至90°之间。当演示台与大转盘从垂直关系逐渐转换成平行关系时，即点A 处矢量夹角θA从0°减小到90°，点B 处矢量夹角θB始终为90°，所以表达式可分别简化为θB=90°。根据上式，随着夹角θA增大，点A 处科氏加速度增大，演示带上点A 处内缩或外扩现象逐渐明显（具体现象由的方向决定），点B 处科氏加速度大小始终不变，在倾斜状态的水平分加速度引起演示带产生向内移或向外移现象。

图2 科氏加速度演示仪实物图

3 结 语

已有的科氏加速度演示仪演示现象单一，效果局限，而自主设计的速度矢量夹角可变的科氏加速度演示仪，不仅结合了已有的水平式和立式的演示仪特点，而且创新设计了角度可调结构，使演示仪的演示内容更加丰富，通过该演示仪的演示，可以增加学生对科氏加速度的兴趣以及对科氏加速度相关知识的理解。

［1］ 哈尔滨工业大学理论力学教研室.理论力学［M］.7 版.北京：高等教育出版社，2009.

［2］ 孙桓，陈作模，葛文杰.机械原理［M］.北京：高等教育出版社，2006.

［3］ 张宏刚.几何法证明科氏加速度［J］.科技信息，2008（19）：217.