阵列感应测井在斜井和水平井中的响应特性

仵杰, 史盼盼, 陈延军, 李戈理, 文强

(西安石油大学光电油气测井与检测教育部重点实验室, 陕西 西安 710065)

0 引 言

许多学者开展了斜井和水平井感应测井响应数值研究。Hardman等[1]和Anderson等[2-3]求解了任意多层介质中发射线圈和接收线圈在任意方向、任意一层介质中的解,并据此计算了双感应测井仪在1个水平地层和多个水平地层中的响应曲线。Rabinovich等人[4]研究了水平井中阵列感应测井数据解释方法,不仅能得到精确的地层信息和井眼附近的侵入电阻率,而且可以反演出仪器距围岩的距离和围岩电阻率。Alpak等[5]数值模拟水平井中泥浆侵入空间分布和分析阵列感应响应特征,指出最深阵列感应数据能够提供无侵入区域的地层电阻率。肖加奇等[6]提出了在水平井中的感应测井数值计算的方法,赵小青等[7]分析了水平井感应测井的影响因素。刘迪仁等[8]研究了在不平整界面地层时双感应测井的响应特征。斜井和水平井中的感应测井响应是三维电磁场数值计算问题,需要解决网格剖分、计算公式推导、大型代数方程求解、场的三维特性分析、程序设计与编程、计算速度、计算精度等等一系列问题。通常的研究很难用于计算分析水平井中的阵列感应响应特性分析。

本文应用COMSOL多物理场有限元软件,成功实现斜井和水平井中的阵列感应响应三维数值计算,以三层地层为例,详细计算研究了斜井和水平井中的阵列感应仪器响应特性,应用三维电磁场分布特性分析响应机理。

1 基于COMSOL软件的斜井和水平井建模

图1是水平井钻井轨道示意图,它由直井段、斜井段(造斜段)和水平段3部分组成。本文研究斜井段和水平段的阵列感应测井响应特性,重点是水平段。实际井况可能存在不规则井眼、不规则侵入、不规则层面等。本文研究最基本的三层模型由目的层和上、下围岩组成。仪器为Baker Atlas公司的高分辨率感应测井仪器HDIL。

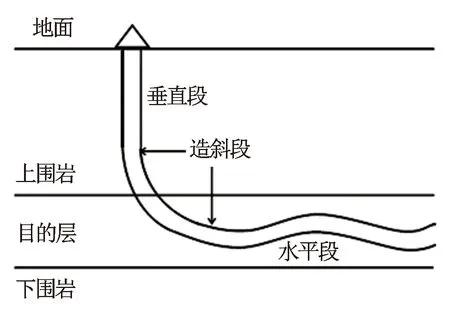
图1 水平井示意图

水平井测井仪器沿预先设定的轨道运动。为了减少数值计算量,数值计算时,仪器水平放置从上围岩向下围岩移动,步长0.2 m。为了同时考察直井和斜井情况,每1个位置仪器沿x轴旋转。从0°～100°,间隔10°。根据这些数据可以生成仪器在模型内沿任意井眼轨道移动的测井曲线。

图2 斜井和水平井三维模型

HDIL的线圈半径近似0.03 m,远小于波长和线圈间距,可以将发射电流源等效为磁偶极子源[9]。仪器为玻璃钢外壳,半径0.045 m,内部填充空气,电导率0 S/m。HDIL仪器有8个工作频率,7个子阵列。在COMSOL软件平台上实现了针对图1问题的阵列感应测井响应三维数值计算(只给出最低频10 kHz时7个子阵列的响应特性研究结果)。

2 水平井阵列感应测井响应特性分析

2.1 水平井位置对水平井中阵列感应测井响应特性的影响

依据某油区的情况,取围岩电导率为1 S/m(电阻率1 Ω·m),目的层电导率1/30 S/m(电阻率30 Ω·m),目的层的层厚为5 m。设层中心为坐标原点,水平井位置从上侧6 m到下侧-5 m变化。图3给出了7个子阵列的视电导率随水平井位置的变化曲线(子阵列1、4和7在水平井和直井中的测井响应)。

(1) 水平井中的7个子阵列[图3(a)],水平井在层界面时,子阵列3开始出现异常尖峰,子阵列间距越长,尖峰越明显;在层中心,由于受围岩影响,测量值从子阵列1到子阵列7逐渐增大;水平井离开围岩与目的层交界面,不同间距子阵列有规律分离。

(2) 对于最短子阵列1[图3(b)],水平井中的响应与直井差别很小,水平井中的响应曲线关于层中点左右对称,直井中不对称,需要平移记录点才能对称。这是因为子阵列由不对称的3线圈组成,在直井中,记录点不是读数最大位置,近似在主接收位置。水平井中,仪器轴与地层面平行时,测量结果与接收线圈在发射线圈的左侧还是右侧无关,不能区分左右,因此没有记录点平移问题。

(3) 对于子阵列4[图3(c)],水平井与直井的差别比子阵列1大。在水平井中,最小值在层中间,数值小于直井,在上下层界面出现2个小尖峰。在直井中,曲线光滑,关于最小值位置左右不对称,记录点偏移比子阵列1大。

(4) 对于最长子阵列7[图3(d)],水平井中的响应与直井明显不一样。水平井中,仪器在层界面时出现明显异常的尖峰,数值比目的层的电导率还小;在目的层中心±1 m范围的读数近似相等,似乎围岩影响相同。在直井中,围岩影响严重,没有出现平直段,目的层中的读数均大于真电导率;响应不对称,记录点平移量最大。

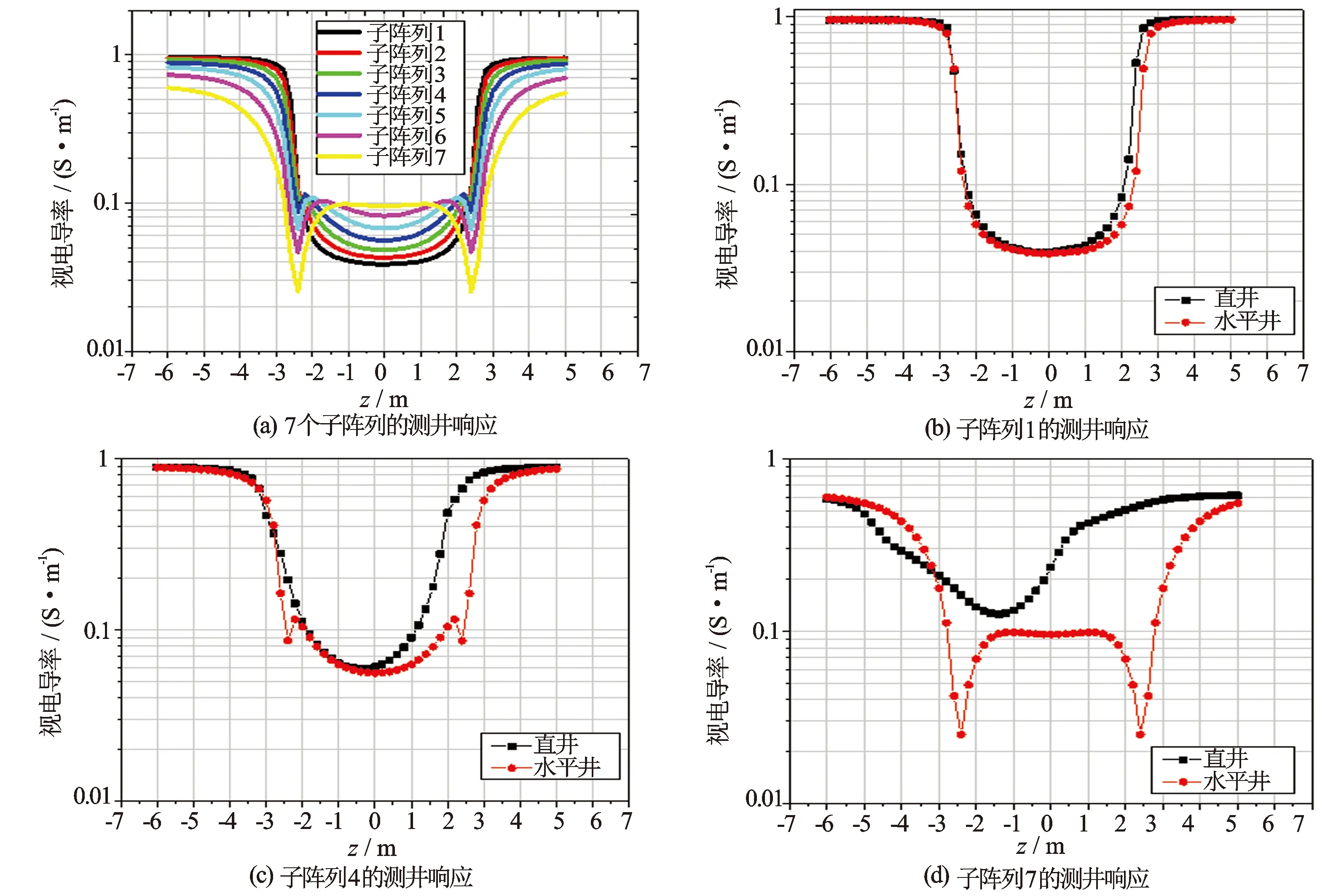
图3 水平井和直井中的阵列感应测井响应特性比较

2.2 目的层层厚变化对水平井中阵列感应测井响应特性的影响

取目的层电导率为1 S/m,围岩电导率为0.01 S/m,水平井位于目的层中心,目的层厚度1～20 m。图4给出了高电阻率围岩[图4(a)]和低电阻率围岩[图4(b)]时7个子阵列响应随层厚的变化曲线。图4表明,当层厚大于4 m时,围岩影响类似于直井,低电阻率(高电导率)围岩影响大。对于高电阻率(低电导率)围岩,各子阵列响应为目的层读数90%对应的层厚分别为2、4、4、6、6、6 m和8 m。低电阻率围岩的相应层厚大得多。

2.3 目的层和围岩电导率及其比度变化对水平井中阵列感应测井响应的影响

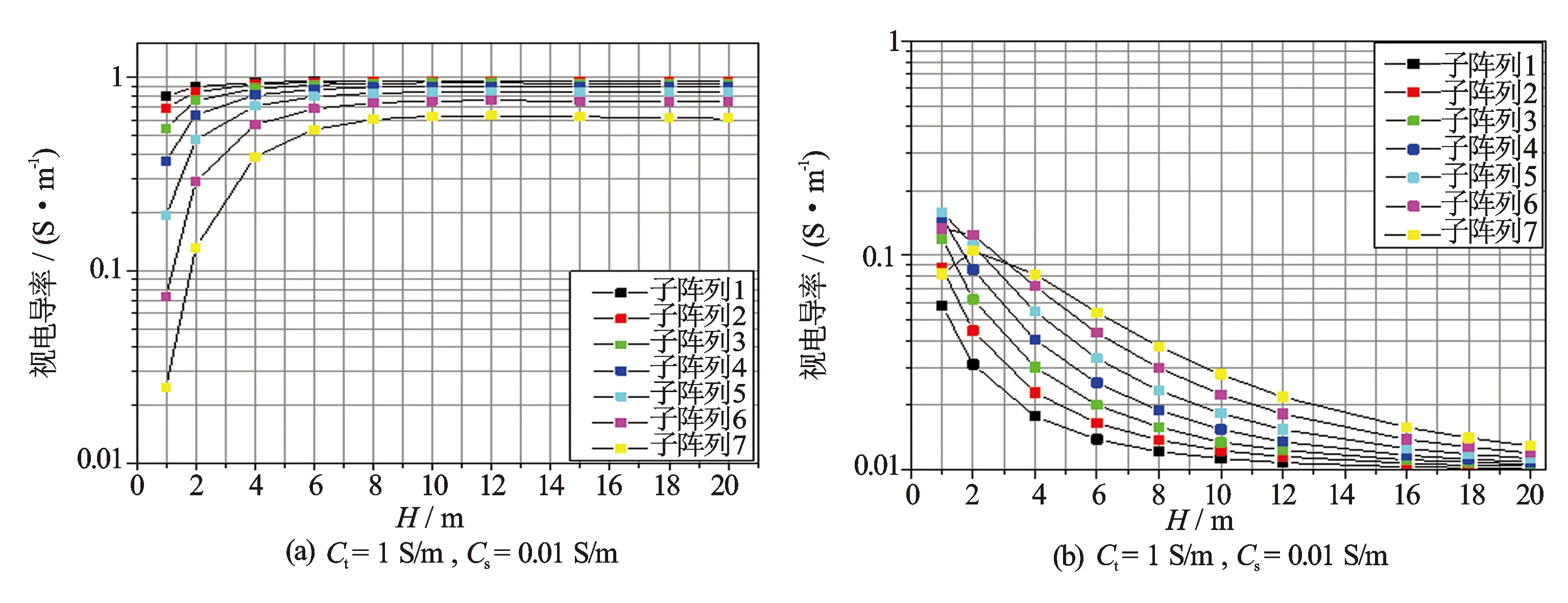
图4 水平井中目的层的层厚变化对测井响应的影响

为了使结果具有较大的适用范围,取电导率为0.001、0.01、0.1、1和10 S/m,目的层和围岩电导率是所有可能的组合,对应的电导率对比度范围10-4～10+4。层厚取1 m薄层和5 m厚层。水平井从层一侧向另一侧移动。结果表明,不同层厚时,目的层和围岩电导率及其对比度对各子阵列的影响不一样,层越薄,对比度越大,影响越复杂。当电导率小于1 S/m时,对比度越大,影响越大。当电导率大于1 S/m时,趋肤效应和对比度影响同时存在。表1给出了水平井在层中心,目的层分别为低电阻率(电导率1 S/m)和高电阻率(电导率0.01 S/m),围岩变化时子阵列1、3、5、6和7的测井响应。

当围岩与地层电导率对比度小于10或者电导率小于1,所有子阵列随对比度增大,响应增大。否则,不同子阵列影响不一样。对于短子阵列,趋肤效应影响小,主要受对比度影响。对于长子阵列6和7,同时受对比度和趋肤效应影响,响应变化复杂。

为了更清楚了解电导率和对比度的影响,图5给出了4种情况下的响应特性。图5(a)和图5(b)是对应图3模型的低电阻率围岩和高电阻率围岩,层厚为1 m薄层,给出了对应图3模型但层厚减小到1 m时的响应曲线,图5(b)是目的层与围岩电导率交换后的响应曲线;图5(c)和图5(d)是对比度分别为0.1和0.01时的情形。

(1) 低电阻率(高电导率)围岩模型[图5(a)]中,仪器位置从高电导率围岩靠近低电导率目的层时, 7个子阵列的关系有规律分离, 与图3(5 m层厚)一致。在目的层中,所有子阵列均分辨出1 m厚地层,但读数不一致,与图3明显不一致。在层界面处,尖峰异常幅度比5 m厚地层小。

(2) 高电阻率(低电导率)围岩模型中[图5(b)],仪器距层边界大于2.5 m,从低电导率围岩靠近高电导率目的层时,7个子阵列的关系是最长子阵列视电导率最大,最短子阵列视电导率最小。当距边界距离小于2.5 m时,不同子阵列视电导率曲线之间的关系随阵列间距依次反转,在层界面附近及目的层里,最长子阵列视电导率最小,最短子阵列视电导率最大。在层界面处,尖峰异常幅度比5 m厚地层明显,所有子阵列均出现尖峰,子阵列5、6和7出现负值。

(3) 图5(c)、图5(d)为层厚5 m时的响应曲线,长阵列在目的层内电导率值小于短阵列,且随着电导率对比度(Cs/Ct)减小,在层界面处长阵列出现负值,当仪器离开边界时,随电导率对比度的减小,围岩影响越大,这与图5(b)规律相同。

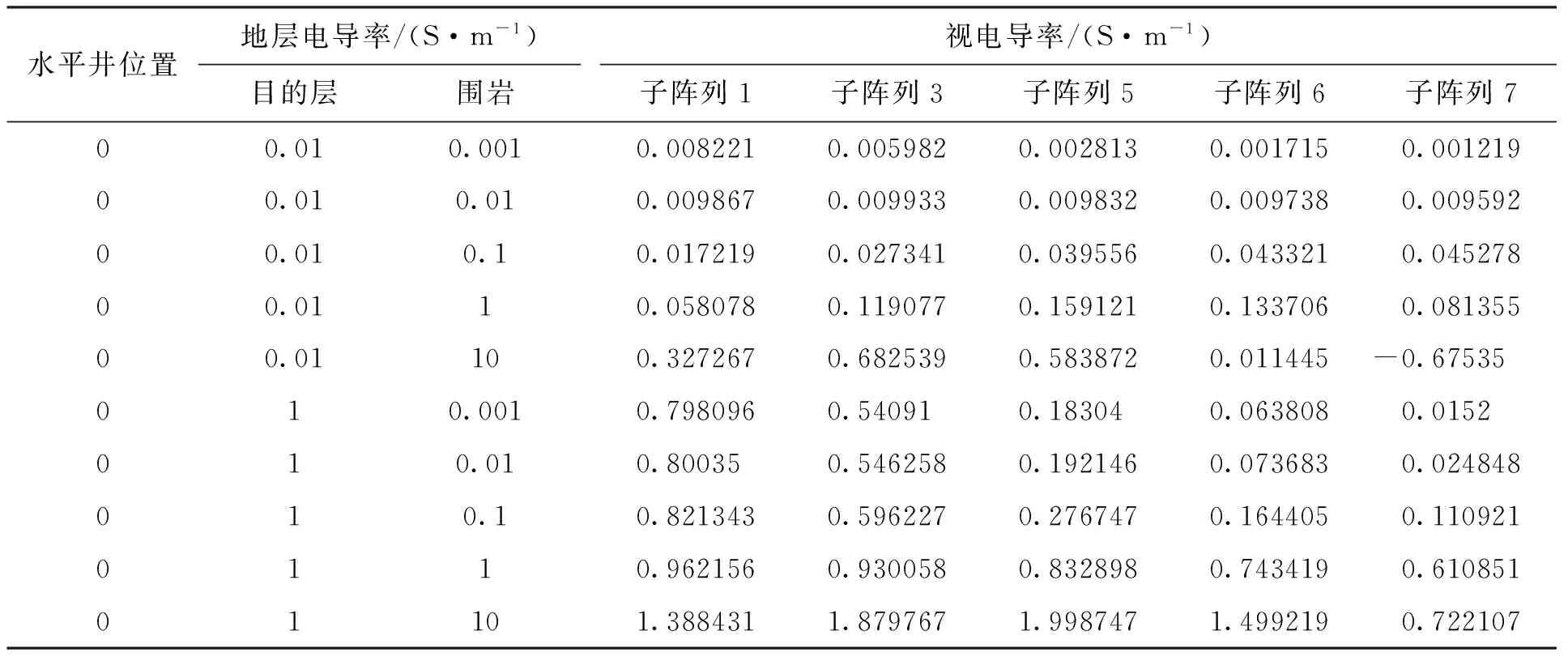
表1 层厚为1 m不同电导率对比度时各子阵列的测井响应

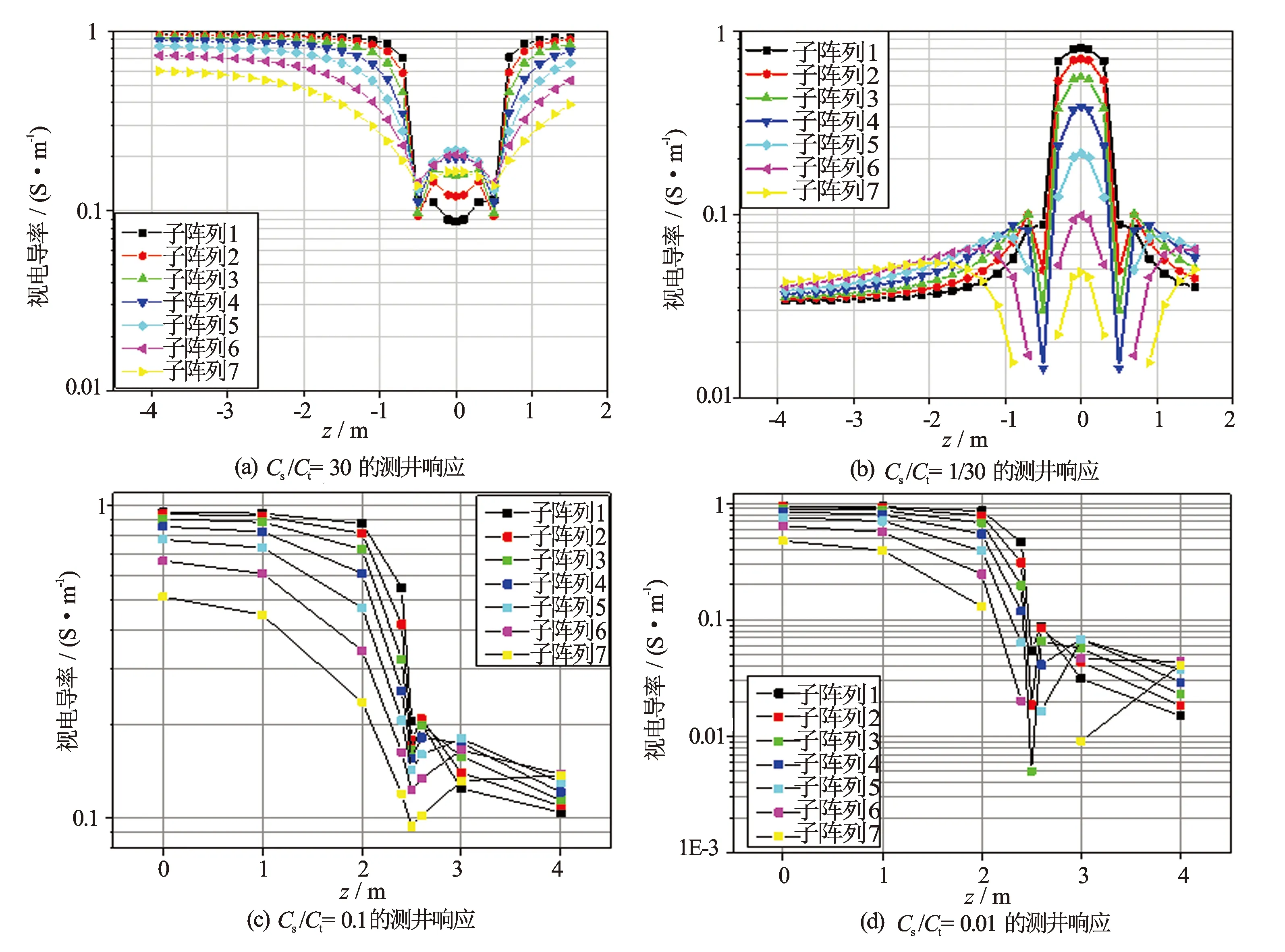
图5 1 m和5 m层厚时电导率对比度对水平井测井响应的影响

3 斜井中的阵列感应测井响应影响

在大斜度井或者水平井的造斜段,井眼与地层法线有一定夹角,即使在水平段,井眼也不是完全水平,而是在一定角度范围内变化。计算分析了地层法线与井眼相对角度从0°～100°变化时测井响应的变化特性。为了分析方便,仍以图3的模型为基准。

3.1 不同倾角下各子阵列测井的响应曲线分析

图6是各子阵列在不同角度时的测井响应曲线,从图6可以看出如下特点:

(1) 当仪器倾角为0°时[图6(a)],即直井中,曲线光滑,没有异常,短子阵列分辨率高,清楚分辨出5 m层厚,最小值读数接近目的层电导率,长子阵列围岩影响严重,分辨率低,读数与真值差别较大。由于仪器记录点不一致,各子阵列的峰值位置不在同一深度。

(2) 当倾角小于30°时[图6(b)],倾角影响较小,曲线特征与直井一致,只有最长子阵列7有一点影响,最小值略低于直井。

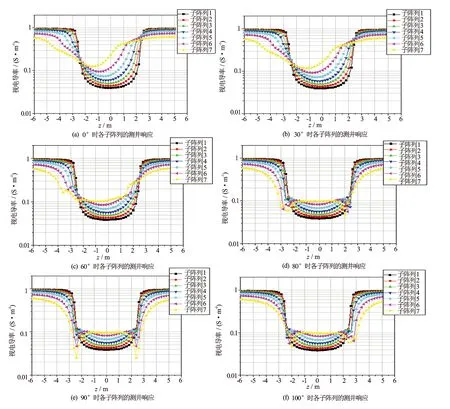
图6 不同倾角下的各子阵列测井响应曲线

(3) 随着倾角增大,倾角影响逐渐增大,尤其是分辨率低,不能分辨层厚的长子阵列。60°时[图6(c)],子阵列5、6和7在层边界左侧出现“尖峰”。大于80°时[图6(d)],所有子阵列在左右层边界出现尖峰异常,90°最明显。90°[图6(e)]时各子阵列的分辨率一致,关于层中点,响应上下对称。

(4) 在90°附近,如果倾角小于90°,当仪器从上向下运动时,发射线圈先到达界面,由于各子阵列记录点不一致,在左侧界面7个子阵列明显分离,右侧界面基本重合,如80°[图6(d)]。如果倾角大于90°时,接收线圈先到达界面,在右侧界面7个子阵列明显分离,左侧界面基本重合,如100°[图6(f)]。对于5 m厚地层,倾角在90°附近±10°变化,目的层中心7个子阵列的读数基本不变。

3.2 仪器倾角变化对于不同子阵列测井响应的影响

为了看清倾角对各子阵列的影响,对图6进行重新整理,按各子阵列绘出(见图7)。

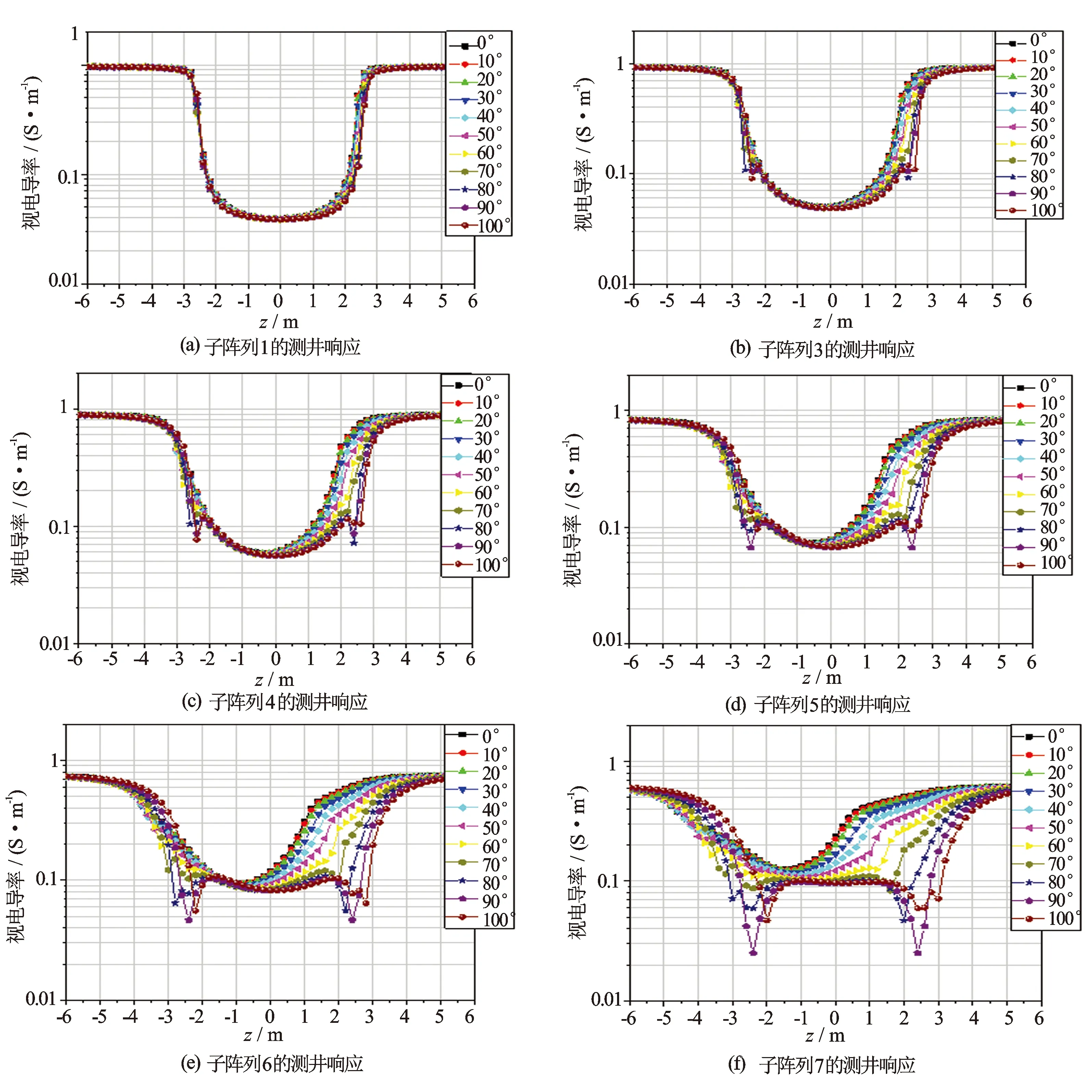
图7 仪器倾角对各子阵列测井响应的影响

(1) 最短阵列1的原始分辨层厚最小(近似1 m),远小于层厚,受倾角影响最小,没有异常尖峰。随子阵列间距增大,分层能力下降,倾角影响增大,异常尖峰逐渐明显,最长子阵列7最明显。

(2) 图7中的曲线以发射线圈为记录点。当倾角小时,不同子阵列最小值位置不一致,随着倾角增大,最小值向层中心移动,90°出现在层中心,大于90°又向另一侧移动。根据7个子阵列的分离和变化特性,可以区分井眼与地层的相对夹角和近似层厚,即判断仪器穿过界面时的空间姿态。用短子阵列识别层厚,用长子阵列识别夹角。Rabinovich等[4]提出了识别仪器距层距离的方法。

3.3 不同电导率对比度对斜井中各子阵列测井响应影响

在计算水平井中测井响应受电导率对比度影响时,同时计算了角度为0°、30°和60°时阵列感应响应。图8选择2种电导率对比度分析不同电导率对斜井中阵列感应测井响应的影响。

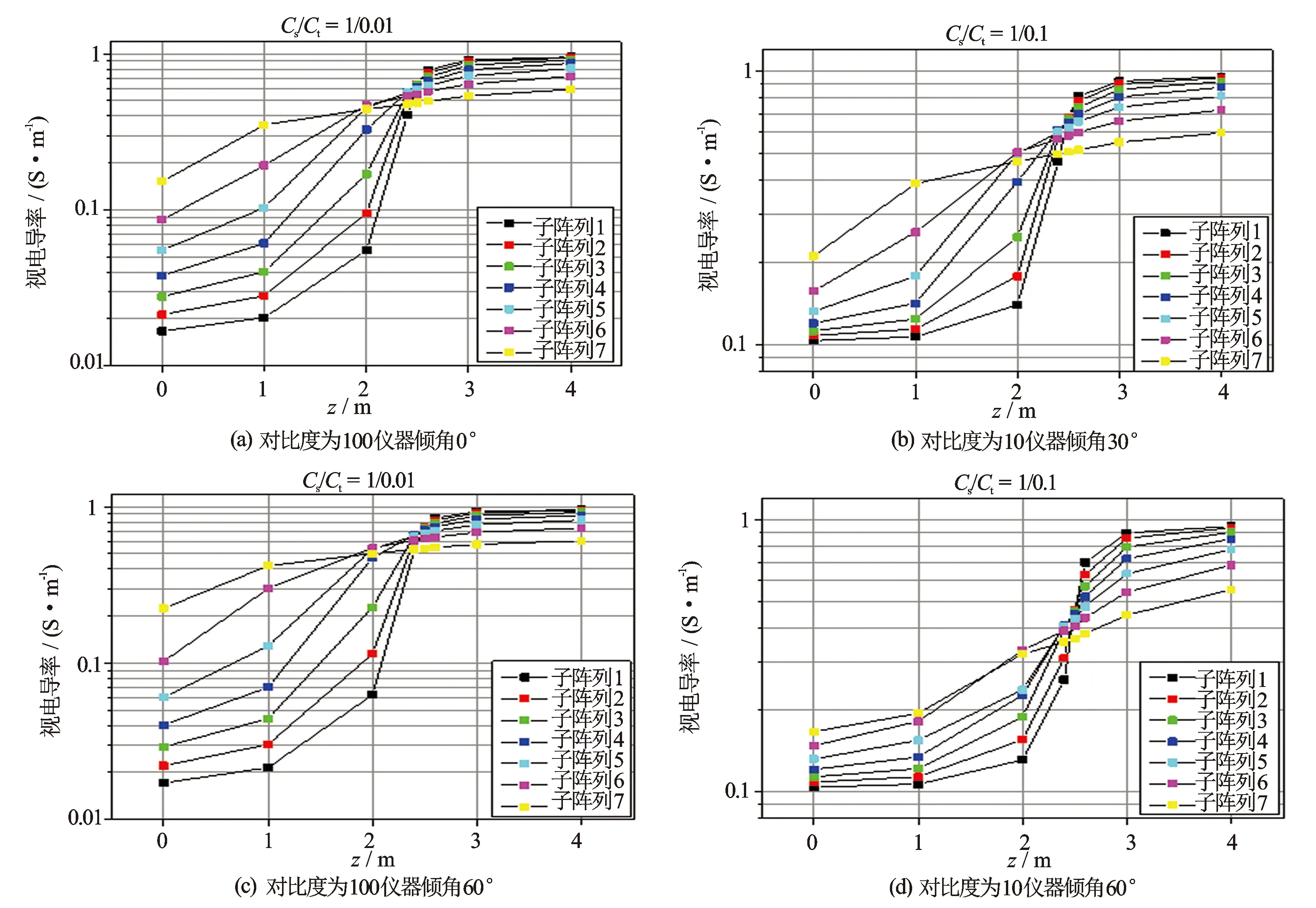
图8 不同电导率对比度情况下各子阵列感应测井响应曲线比较

仪器倾角较小时[图8(a)和图8(b)],随着电导率对比(Cs/Ct)减小,各子阵列受围岩影响较小,电导率曲线趋势变化不大,与图6(b)基本一致。当仪器倾角较大时[见图8(c)和图8(d)],随着电导率对比(Cs/Ct)减小,各子阵列感应测井受围岩影响较大,电导率曲线在目的层中逐渐集中在一起,这与图6(c)相似。

4 阵列感应测井响应特性的机理分析

长子阵列在水平井时与直井明显不同,薄层时,所有子阵列与直井明显不一致。利用COMSOL软件后处理功能绘图分析了导致如此大差别的原因和机理。

根据电磁感应原理,接收电压中与地层紧密相关的信号由导电地层中的涡流产生,涡流的空间分布特征决定了接收线圈中的信号来源和信号大小。

根据Maxwell方程电场和电流的交界面条件,可以得到电流穿过2种不同电导率媒质时的折射公式[10]

(1)

式中,γ1为电流从电导率σ1进入时的入射角;γ2为电流从电导率σ2出去时的折射角。

图3的5 m厚模型中,围岩电导率=1 S/m,目的层电导率=1/30 S/m。当电流从低电导率目的层进入高电导率围岩时,比值=1/30,由式(1)可以计算出,当入射角γ1为10.7°时,折射角γ2等于80°,即,电流很容易进入高电导率(低电阻率)地层。相反,当电流从高电导率地层到进入低电导率地层时,比值=30,折射角很小,即,电流很难进入低电导率(高电阻率)地层。

水平井中仪器轴与地层面平行,线圈面垂直于地层面,线圈中的交变电流源首先产生很强的一次交变磁场。根据电磁感应原理,交变磁场产生交变电场。在周围导电地层中将产生交变涡流。在直井中,涡流与仪器轴同心;在水平井中,涡流以不同角度穿越不同电导率之间的层边界。穿出与进入角度的关系满足式(1)描述的电流折射定律。折射电流将形成复杂的空间流动,同时产生复杂的空间磁场分布,接收线圈中电压的大小不仅与两侧电导率有关,而且与交界面和仪器轴夹角有关。此外,距发射线圈不同位置,接收的信号也不一样。针对上述情况,进行水平井中阵列感应的响应特征解释。

图9 穿过上围岩与目的层交界面的涡流空间流线图

设仪器放在z=2.4 m位置,距上边界0.1 m。此时,仪器在低电导率目的层,围岩是高电导率地层。图9是穿过层界面的空间闭合涡流流线图,蓝色流线表示仪器中心处yoz面形成闭合涡流曲线,红线流线表示在层界面附近的形成的闭合涡流曲线。图10同时绘出了距发射线圈不同位置的电流密度模等值图和涡流流向图。曲线颜色表示与仪器垂直的yoz面上电流密度模大小分布图,带箭头的黑线表示由Imag(Jy)与Imag(Jz)构成的归一化涡流流向图。在10 kHz工作频率时,接收线圈中的主要信号是x方向的磁场虚部,该磁场由Imag(Jy)和Imag(Jz)产生。从图9可知,穿过界面的电流线在仪器附近,近似与界面平行;较远处才形成与仪器轴垂直的闭合线。仪器越接近层边界,这种现象越严重。图10清楚地显示了yoz面上电流线具有如下特征。

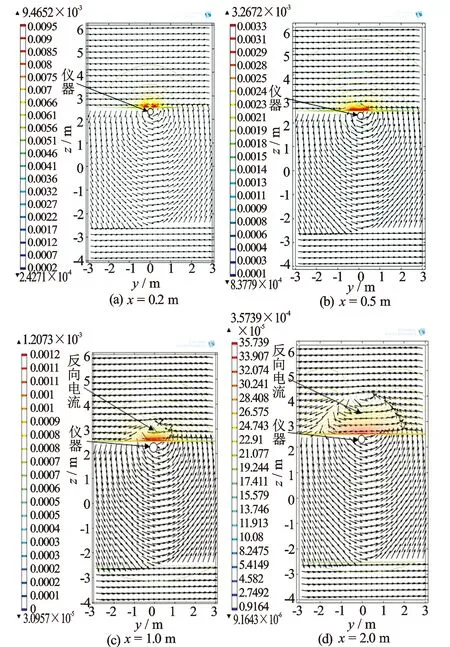
图10 距发射线圈不同位置yoz截面上电流密度模分布和Imag(Jy)与Imag(Jz)构成的电流线

(1) 发射线圈电流源在地层中建立的涡流,首先从低电导率目的层进入高电导率围岩,由式(1)知,很小入射角均可产生很大折射角,电流很容易进入围岩。其次,当电流由高电导率围岩流回低电导率目的层时,折射角小,电流不容易流回目的层。最终结果,围岩中的电流线近似平行层边界,目的层中的电流线仍为绕发射线圈的同心涡流。这种折射现象与侧向测井中直流电流过不同电导率界面类似。

(2) 距发射线圈不同位置的yoz面上,随着离发射线圈距离的增大,电流密度模逐渐减小,且在上围岩处出现反向电流。在x=0.2 m的yoz面上,电流围住仪器轴,磁场集中在仪器附近。随着与发射线圈距离的增加,仪器周围电流线和磁场产生复杂变化。当x=1.0 m,在仪器轴正对的围岩中出现与正常电流流动方向相反的电流,没有围住仪器轴。当x=2.0 m时,清楚可见这种现象。这部分电流在接收线圈中将产生与正常电流相反的磁场,减弱正常接收信号。这就解释了图4中为什么短子阵列受界面影响小,而长子阵列受界面影响大。电导率对比度越大,以上现象越严重。当围岩电导率较大时,这种现象与趋肤效应同时存在,导致测量信号变化特性更复杂。

随着仪器轴与地层法线的夹角减小,界面的面电流减弱。当仪器轴与地层法线一致,即直井时,电流不穿过层界面,交界面不存在折射现象,涡流均与仪器轴同心,磁场在交界面不产生突变,因而接收信号不会出现尖峰异常现象。

4 结 论

(1) 水平井中的阵列感应测井响应特性不但与目的层层厚、目的层和围岩电导率对比度对有关,而且与目的层和围岩电导率大小以及子阵列间距有关,尤其是水平井在地层中的位置。对高分辨率阵列感应测井仪器HDIL的10 kHz响应研究表明,当层厚大于仪器分层厚度时,水平井与直井测井响应接近;当层厚小于仪器分层厚度时,水平井与直井测井响应明显不同,在水平井进出界面时,测井响应出现明显尖峰;水平井中的测井响应同时受电导率对比度、趋肤效应和界面电荷堆积的影响,比直井复杂的多。

(2) 在斜井中,当仪器轴线与地层法线相对倾角小于30°,各子阵列受倾角影响小。当倾角从30°～80°变化时,从短子阵列到长子阵列,倾角影响逐渐增大,主接收从高电阻率进入低电阻率,界面出现尖峰现象。当倾角在90°±10°范围内时,仪器进出界面时均出现尖峰现象。电导率对比度在倾角小时,对测井响应影响不明显,在倾角大时,特别是在90°时,测井响应的尖峰现象严重。

(3) 通过绘制水平井中距发射线圈不同横截面上的磁场分布图、涡流强度和流向图,展示了涡流在不同电导率交界面的折射现象,折射导致涡流沿地层表面流动,形成新的旋涡,距发射线圈越远,电导率对比度越大,越明显。这些现象揭示了水平井阵列感应测井不同子阵列响应特征不一样的机理。

(4) 研究结论对解释水平井和大斜度井中阵列感应测井的响应特征具有重要的理论和实际意义。

参考文献:

[1] Hardman R H, Shen L C. Theory of Induction Sonde in Dipping Beds [J]. Geophysics, 1986, 51(3): 800-809.

[2] Anderson B, Safinya K A, Habaseby B. Effects of Dipping Beds on the Response of Induction Tools [J]. SPE 15488, 1986.

[3] Anderson B, Bonnet S, Rosthai R. Response of 2-MHz LWD Resistivity and Wireline Induction Tools in Dipping Beds and Laminated Formations [J]. Log Analyst, 1992, 33(5): 461-475.

[4] Rabinovich M, Beard D, Geldmacher I. Interpretation of Induction Logging Data in Horizontal Wells [J]. SPWLA 41th Annual Logging Symposium, June 4-7, 2000.

[5] Alpak F O, Dussan E B, Habashy T M. Numerical Simulation of Mud-Filtrate Invasion in Horizontal Wells and Sensitivity of Analysis of Array Induction Tool [J]. Geophysics, 2002, 44(6): 396-411.

[6] 肖加奇, 张庚骥. 水平井和大斜度井中的感应测井响应计算 [J]. 地球物理学报, 1995, 38(3): 396-404.

[7] 赵小青, 张会芳, 潘保芝, 等. 水平井感应测井影响因素分析及在水淹层解释中的应用 [J]. 测井技术, 2010, 34(1): 42-46.

[8] 刘迪仁, 谢伟彪, 殷秋丽. 水平井不平整界面地层中感应测井模拟及影响分析 [J]. 石油物探, 2012, 51(1): 86-97.

[9] 张建华, 刘振华, 仵杰. 电法测井原理与应用 [M]. 西安: 西北大学出版社, 2002: 121-125.

[10] 晁立东, 仵杰, 王仲奕. 工程电磁场基础 [M]. 西安: 西北工业大学出版社, 2002: 154-192.