岩石复电阻率频谱反演研究
林小稳, 柯式镇, 贺秋丽, 许巍, 舒心, 张琪
(1.中国石油大学(北京)地球物理与信息工程学院, 北京 102249; 2.中国石油大学(北京)油气资源与探测国家重点实验室, 北京 102249; 3.中国石油集团测井有限公司技术中心, 陕西 西安 710077)
0 引 言
激发极化法(IP)在地球物理勘探领域已经被广泛应用。复电阻率法(CR)又称频谱激电法(SIP),是20世纪70年代发展起来的激电分支方法[1]。在对岩石复电阻率研究中通过等效电路建立模型模拟岩石的频散特性,使用最为广泛的是Cole-Cole模型。利用实验室岩心测量数据,选择合适的算法反演出Cole-Cole模型中的电频谱参数,进而对解释模型进行标定是复电阻率测井资料解释的核心问题。国内外学者对模型参数的反演作了许多研究,Jaggar等于1988年提出了基于马奎特算法的反演[2]。2001年,J.Xiang等提出了基于多重最小二乘估计的直接反演算法,该方法不需要任何中间变量的介入,也不用对参数初始值进行估计,可反演得到一阶Cole-Cole模型中的4个参数[3]。2005年曹中林引入遗传算法对一阶Cole-Cole模型以及和形式的二阶模型进行了反演,并与马奎特算法进行了对比[4-5]。2006年童茂松等引入模拟退火算法对一阶Cole-Cole模型、基于乘积形式的二阶模型及Dias模型进行了反演,并提出基于乘积形式的二阶复Cole-Cole模型比一阶模型更具有优势[6]。在实际工作中如何选择合适的模型以及反演算法,国内外学者对此没有作过深入系统的研究,也没有给出过明确的结论。
本文在100 Hz~10 MHz频率范围内测量了多组人造砂岩样品的复电阻率频谱曲线并进行了反演。在反演复电阻率频谱时,使用局部寻优的最小二乘法以及在全局寻优中的2种算法——单点搜索的模拟退火算法和并行群体搜索的遗传算法。本文利用这3种算法结合基于乘积形式的二阶Cole-Cole模型对理论模型和实测数据分别进行了反演,综合对比了这3种算法的优缺点,验证了二阶Cole-Cole乘积模型与实测数据的适配性,为反演算法的选择提供了指导。
1 复电阻率测井
复电阻率测井方法是基于地层岩石电阻率的频散特性而发展起来的一种新的测井方法。它充分利用了岩石的频散信息,改变了仅考虑探测空间范围影响而忽视岩石频散性质的传统认识,在一定程度上克服了地层水矿化度的影响,可以更加直观地反映含油性,提高对油层的识别能力。利用复电阻率测井数据可以按照图1所示的流程计算含油气饱和度[7],在这一流程中,利用岩心实验数据反演出Cole-Cole模型中的频谱参数对模型进行标定是最为基础也是最为核心的一步,反演所得参数的准确性将影响模型标定的准确性,最终影响储层评价的准确性。
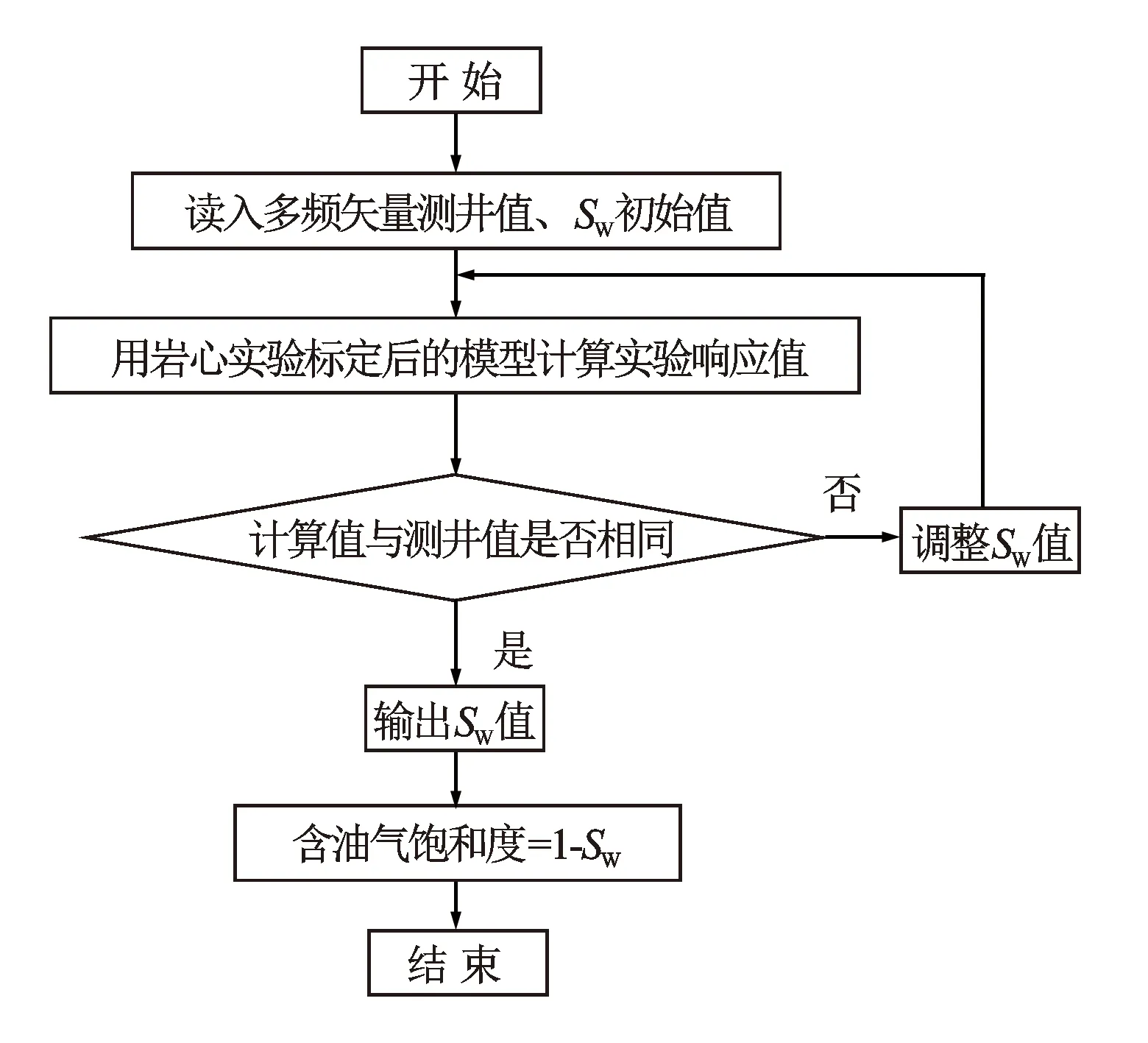
图1 复电阻率测井解释流程图
2 Cole-Cole模型
Cole-Cole模型是20世纪40年代初期K.S.Cole和R.H.Cole首先提出并用来描述电解质的介电极化效应[8],后人在此基础上不断研究,逐渐完善了这一模型。1978年,Pelton等通过研究认为,岩石的激电效应与Cole-Cole模型相符合,并将其引入到地球物理勘查中,由此奠定了复电阻率法的基础。Pelton认为岩石复电阻率随频率的变化(即复电阻率频谱)可表示[9]为
(1)
式中,ρ(ω)为复电阻率,Ω·m;ρ0为零频电阻率,表征导电性强弱,Ω·m;m为极化率,表征激电效应强弱;τ为时间常数,表征激电效应特性;c为频率相关系数,表征频谱或时间谱陡缓;ω为角频率。
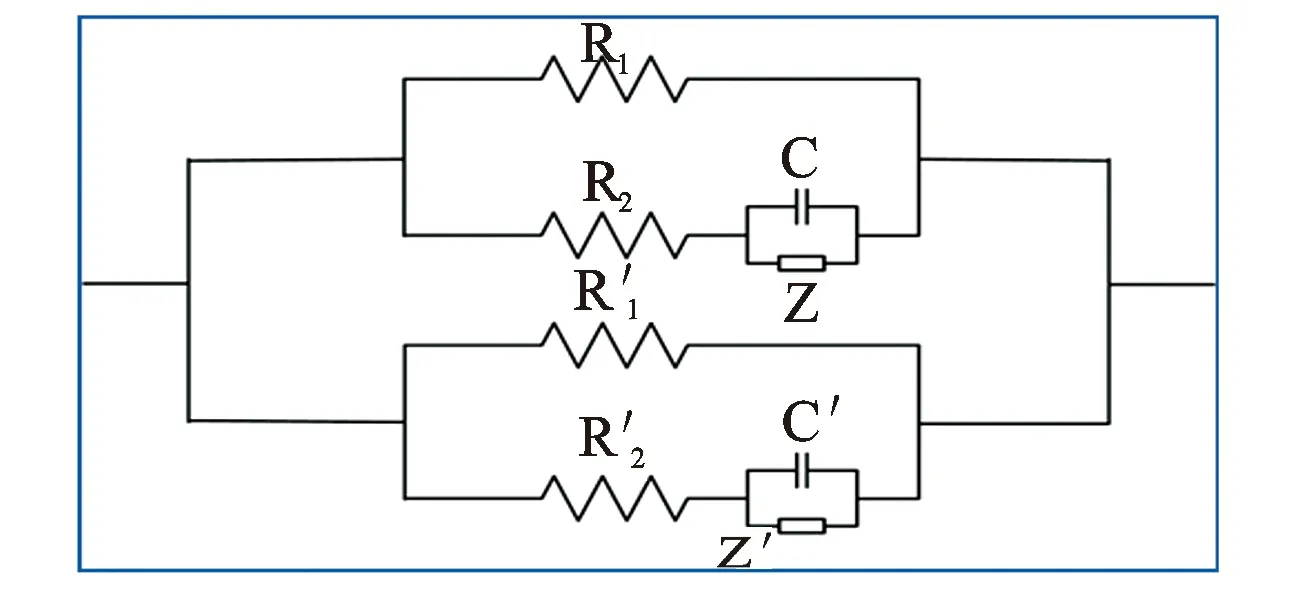
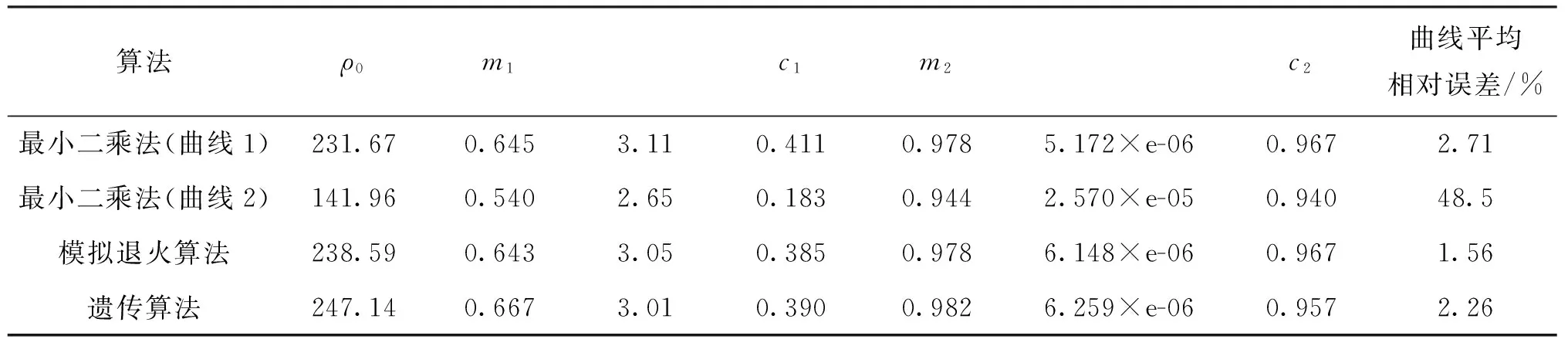
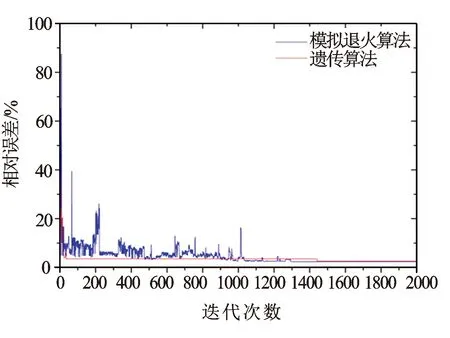
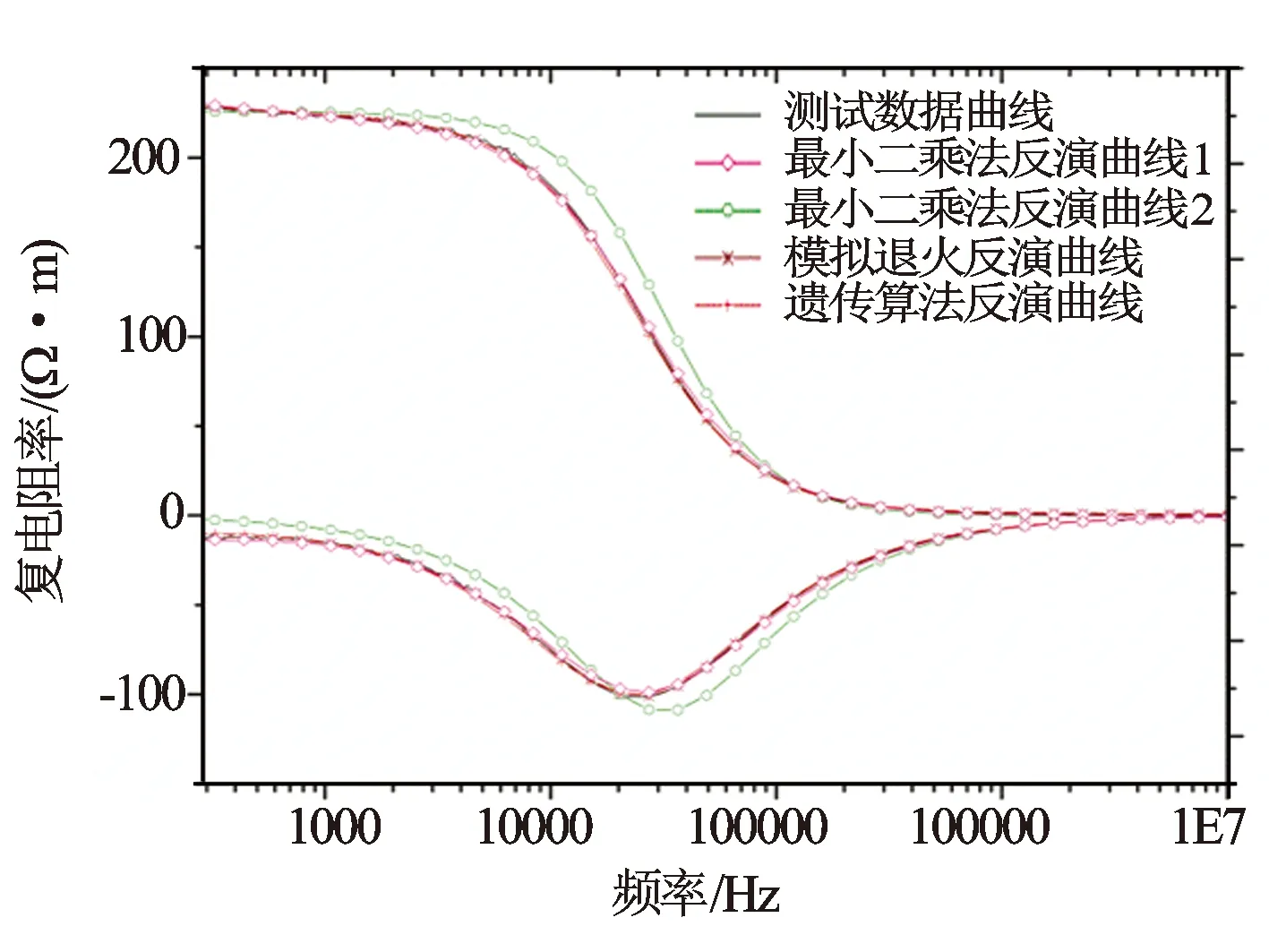
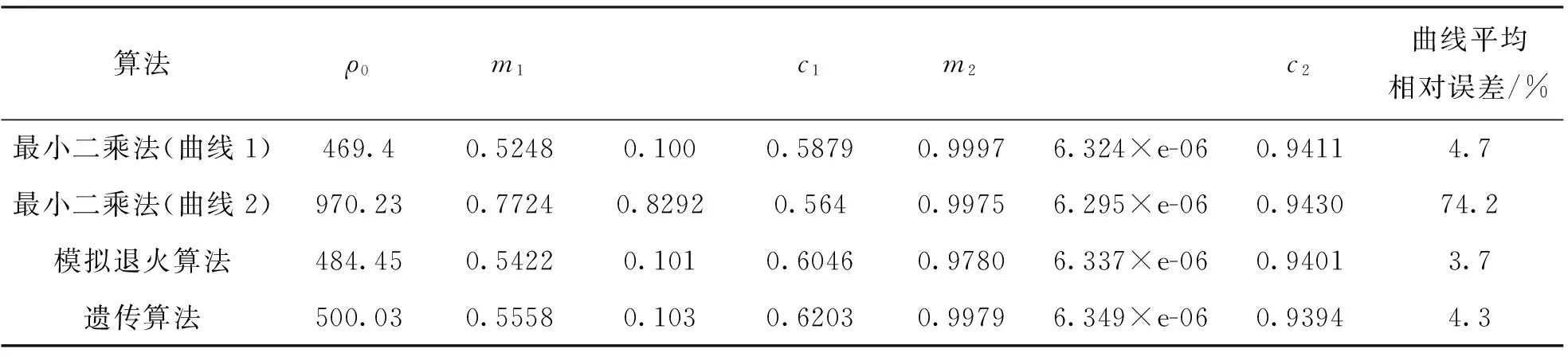
一阶Cole-Cole模型的复电阻率曲线实部表现为单斜坡,虚部为单波谷的特征,而大多数实测曲线却表现为多斜坡、多波谷特征。为了更好地计算岩石复电阻率的频散特性,Pelton等用2个Cole-Cole模型描述饱和盐水岩石的频散现象,一个表征界面极化,另一个表征盐水偶极子极化[10]。二阶Cole-Cole模型有并联和串联2种形式,其等效电路图(二阶)如图2和图3所示。本文所介绍的反演算法基于二阶(N=2)并联形式的Cole-Cole模型,且其反演得到的参数极化率mi、频率相关系数ci要在0 (2) 式中各参数的意义与一阶Cole-Cole模型中参数的意义相同。 图2 二阶串联Cole-Cole模型等效电路 图3 二阶并联Cole-Cole模型等效电路 实验室对岩石复电阻率频谱的测量有电极法和线圈法。本文采用如图4所示的电极法测量[11]。 图4 岩心复电阻率测量系统 实验测量系统结构由信号发生器、功率放大器、取样移相电路、测量电极系、岩心夹持器、锁相放大器、数字存储示波器和计算机组成。各个仪器之间采用通用并行接口总线相连,以计算机作为控制中心,控制各个仪器的工作,与控制软件一起构成完整的扫频测量系统[12]。 最小二乘法[13]让实测数据和估计数据之间的距离平方和最小,这是最小二乘法使用的逼近原则。 模拟退火算法的思想来源于对固体退火降温过程的模拟,即将固体加温至充分高,再让其充分冷却。模拟退火算法是一种启发式随机搜索方法,但它在搜索策略上与传统的随机搜索方法不同,它不仅引入了适当的随机因素,而且还引入了物理系统退火过程的自然机理[14]。模拟退火算法从某一较高初温出发,伴随温度参数不断下降,结合概率突跳特性在解空间中随机寻找目标函数的全局最优解。 遗传算法是一种自适应全局优化概率搜索算法[15]。遗传算法模拟自然进化中优胜劣汰、适者生存的原理,与传统的搜索策略不同,遗传算法不是简单的单点搜索,而是并行群体搜索,可以同时处理群体中的多个个体[16]。 利用最小二乘法、模拟退火算法以及遗传算法在100 Hz~10 MHz频率范围内对二阶并联形式的Cole-Cole理论模型在不同的信噪比时进行反演,反演出公式中的7个参数和复电阻率曲线。表1给出了理论模型参数和反演初始参数;图5所示是在信噪比为30时反演所得曲线。使用这3种算法对理论模型(信噪比为30)进行了20次反演,反演所得参数及曲线平均相对误差如表2所示。 表1 理论模型参数及反演初始参数 表2 理论模型反演结果平均相对误差表 图6 理论模型反演迭代收敛图 反演时对于最小二乘法设置了2组初值(见表1)。第1组设置恰当;第2组设置不恰当以作为第1组的对比。反演结果表明,使用第1组初始值时最小二乘法可以得到准确的解;使用第2组初始值时最小二乘法所得的结果误差很大,这恰恰反映了最小二乘法对初始值具有依赖性,容易陷入局部极值而得不到准确结果的局限性。模拟退火算法进行反演,使用第2组初始值初始值依然可以得到准确的反演结果,这也验证了作为全局寻优的模拟退火算法,摆脱了对初始值的依赖性,避免陷入局部极值;针对群体开始搜索的遗传算法,作为一种并行的全局寻优算法,同时对模型的7个参数进行并行搜索,也可以得到准确的反演结果。对于这3种算法,最小二乘法耗时最短,遗传算法耗时最长。算法的运行时间受算法运行平台配置、算法内部优化等影响,本文比较的是模拟退火算法和遗传算法的收敛速度。图6所示是同时循环2 000次时模拟退火算法与遗传算法的迭代收敛图。由图6可知模拟退火算法的收敛速度慢于遗传算法,这是因为模拟退火算法是通过搜索邻域逐渐搜索全局最优解,对整个搜索空间的状况了解不多,不便于使搜索过程进入最有希望的搜索区域,从而使得模拟退火算法的运算效率不高;遗传算法针对群体开始搜索,运算效率较高,但遗传算法对局部搜索的并不充分。在实现过程中,模拟退火算法更加简单,容易实现;遗传算法过程繁琐,计算过程中有较多的参数,实现过程比较复杂。 通过对理论模型反演,验证了模拟退火算法和遗传算法在反演工作中的可行性。利用第3部分所述的实验测量系统测量了不同饱和度人造岩心的复电阻率数据,利用所测数据中第1组的实验实测数据的反演结果曲线图如图7所示,所选岩心的孔隙度为0.27,矿化度为1 kmg/L,含水饱和度为100%。反演时与理论模型反演相同,也设置了2组初始值,对实测数据进行了20次反演,反演得出的7个参数和曲线平均相对误差如表3所示。由实测数据的反演结果可得出与前文一致的结论,二阶乘积形式的Cole-Cole模型可以很好的与实测数据相匹配。通过对这3种算法的综合对比,可以看出全局寻优的模拟退火算法因其不依赖初始值的设置,可以找到全局最优解,过程简单明了,容易实现的特性在实际工作中更有优势。 图7 实测数据反演曲线图 算法ρ0m1c1m2c2曲线平均相对误差/%最小二乘法(曲线1)469.40.52480.1000.58790.99976.324×e-060.94114.7最小二乘法(曲线2)970.230.77240.82920.5640.99756.295×e-060.943074.2模拟退火算法484.450.54220.1010.60460.97806.337×e-060.94013.7遗传算法500.030.55580.1030.62030.99796.349×e-060.93944.3 (1) 基于乘积形式的二阶Cole-Cole可以很好地匹配实测数据,可以应用于实际反演。 (2) 在初值设置合理时,最小二乘法可以快速准确地得到反演结果;但当初值设置不合理时最小二乘法容易陷入局部极值,无法得到正确的反演结果,因此,使用最小二乘法时需要对初始值进行估计,容易带来误差。 (3) 模拟退火算法和遗传算法这2种全局寻优算法,不依赖初始值的设置,避免了陷入局部极值,可以准确得到全局最优解,反演效果较好。 (4) 模拟退火算法由单点开始搜索领域逐渐搜索全局最优解,运算效率不高,但过程简单明了,容易实现;遗传算法针对群体开始并行搜索,运算效率较高,但实现过程参数较多,比较复杂。 (5) 实际工作中使用模拟退火算法较好,摆脱了对初始值的依赖,容易实现,可以提高工作效率。 参考文献: [1] Lesmes D P, Frye K M. Influence of Pore Fluid Chemistry on the Complex Conductivity and Induced Polarization Responses of Berea Sandstone [J]. Journal of Geophysical Research, 2001, 106: 4079-4090. [2] Jaggar S R, Fell P A. Forward and Inverse Cole-Cole Modeling in the Analysis of Frequency Domain Electrical Impedance Data [J]. Exploration Geophysics, 1988, 19: 463-470. [3] Xiang J, et al. Direct Inversion of the Apparent Complex-resistivity Spectrum [J]. Geophysics, 2000, 66(5): 1399-1404. [4] Cao Z L, et al. Inversion Study of Spectral Induced Polarization Based on Improved Genetic Algorithm [C]∥Progress in Electromagnetic Research Symposium, Hangzhou, 2005. [5] 曹中林, 昌彦君, 等. 基于演化算法的复电阻率频谱参数反演 [J]. 工程地球物理学报, 2005, 2(1): 33-38. [6] 童茂松, 丁柱. 岩石复电阻率频谱模型参数的反演 [J]. 测井技术, 2006, 30(4): 303-305. [7] 柯式镇, 冯启宁, 何亿成, 等. 电极法复电阻率测井研究 [J]. 石油学报, 2006, 27(2): 89-82. [8] Cole K S, Cole R H. Dispersion and Absorption in Dielectrics [J]. Chem Phys, 1941, 1: 341-351. [9] Pelton W H, Jones N B, et al. Mineral Discrimination and Removal of Inductive Coupling with Muti-frequency IP [J]. Geophysics, 1978, 43(3): 588-609. [10] Pelton W H, Smith B D, Sill W R. Interpretation of Complex Resistivity and Dielectric Data, part II [J]. Geophysics, 1984, 29(4): 11-45. [11] 张雷洁, 柯式镇, 等. 40 Hz~110 MHz岩石复电阻率频谱实验测量 [C]∥中国地球物理2013——第二十专题论文集, 中国地球物理学会第二十九届年会, 昆明, 2013. [12] 柯式镇, 冯启宁, 孙艳茹. 复电阻率频散模型及其参数的获取方法 [J]. 测井技术, 1999, 23(6): 416-418. [13] Plackett R L. The Discovery of the Method of Least Squares [J]. Biometrika, 1972, 59: 239-251. [14] Kirkpatrick S, Gelatt C D, Vecchi M P. Optimization by Simulated Annealing [J]. Science, 1983, 220(4598): 671-680. [15] Stoffa P L, Sen M K. Non-linear Multiparameter Optimization Using Genetic Algorithm: Inversion of Plane Wave Seismograms [J]. Geophysics, 1991, 56: 1794-1810. [16] Hu B, Tang G, Ma J W, et al. Parametric Inversion of Viscoelastic Media from VSP Data Using a Genetic Algorithm [J]. Applied Geophysics, 2007, 4(3): 194-200.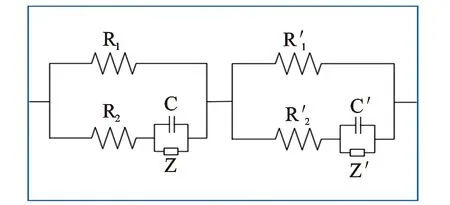
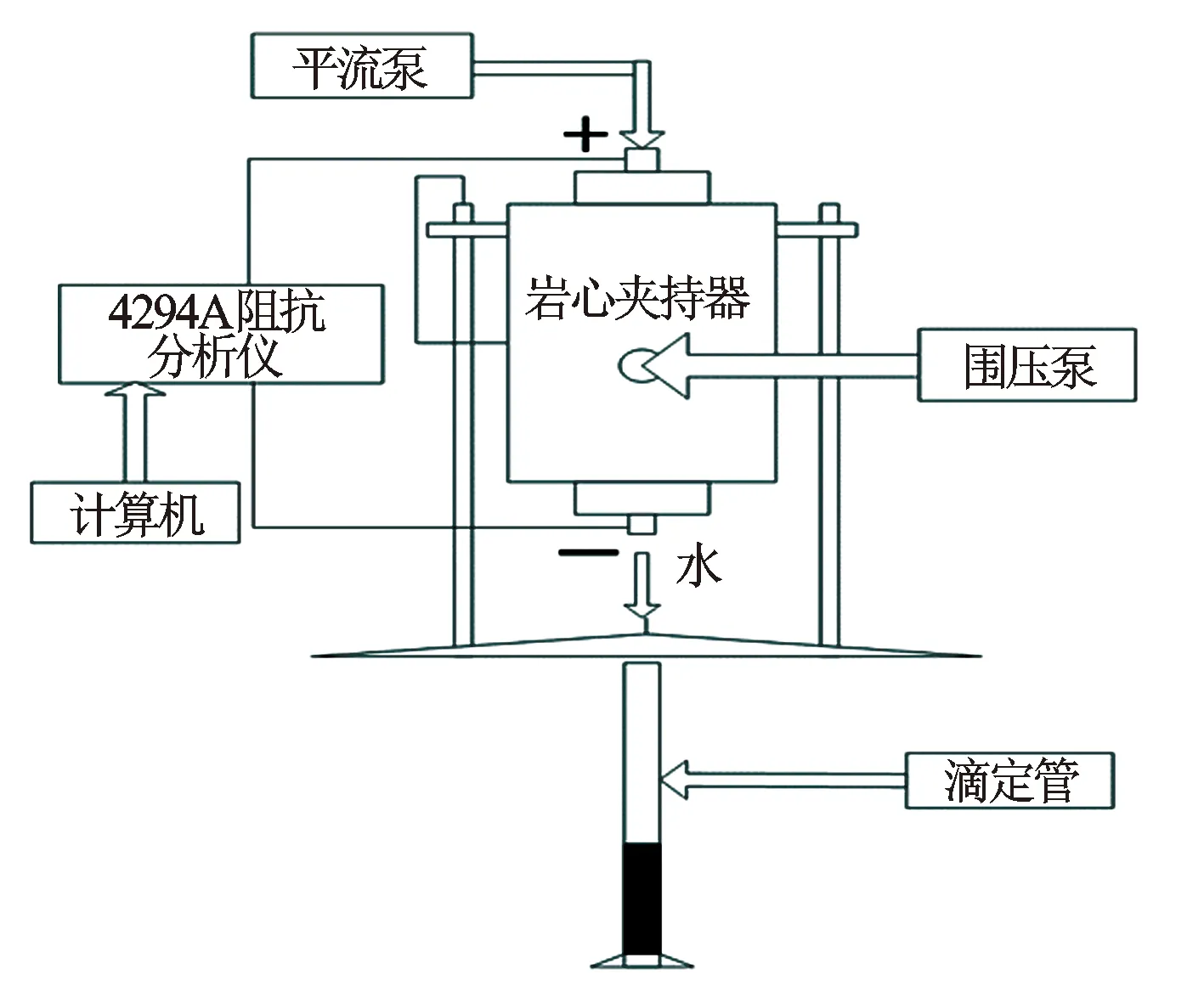
3 实验测量系统
4 反演算法
5 反演结果分析

6 结 论

