基于相渗分析纯岩石电阻率增大系数与含水饱和度关系

张军, 王晓畅, 胡瑶, 李军, 苏俊磊

(中国石油化工股份有限公司石油勘探开发研究院, 北京 100083)

0 引 言

G.E.Archie[1]发表的砂岩电阻率的定律中关于电阻率增大系数与含水饱和度关系部分可理解为,在双对数坐标下,纯净砂岩电阻率增大系数与含水饱和度呈线性关系。G.E.Archie的研究成果主要基于取自美国海湾地区的中高孔隙度纯砂岩岩心样本岩电实验测量结果。全世界范围内的应用表明,除了砂岩,阿尔奇公式在碳酸盐岩、火山岩中也有一定的适用性,阿尔奇公式已成为测井地层评价的基础公式[2-6]。针对致密砂岩等复杂储层的岩电实验发现,电阻率增大系数与含水饱和度关系呈现非阿尔奇现象[7-14],即当含水饱和度较小时,电阻率增大系数明显向下偏转,双对数坐标下与含水饱和度不再呈现线性关系。如何解释复杂储层的非阿尔奇现象,进而对阿尔奇的形式进行改进(或更准确地确定阿尔奇公式参数)成为测井地层评价的一个研究热点。

电阻率与渗透率都是岩石的固有性质,取决于岩石的成分、孔隙结构等因素[5-6];岩石导电与渗流具有相似的过程[15-20],电阻率增大系数与相对渗透率都是含水饱和度的函数。对同一岩石样品,电阻率增大系数与相对渗透率应有一定的联系;另一方面,岩石导电与渗流又存在差异,岩石中常常存在较细小的孔喉,在一定的温度、驱动压差条件下,这些孔喉可能并不参与渗流,但却可能参与导电(前提是可以形成闭合的导电通路)。本文尝试结合岩石的渗流特征研究岩石电阻率增大系数与含水饱和度的关系。

1 岩石渗流模型分析

岩石中孔喉较大的连通孔隙空间对岩石渗透性贡献较大,岩石渗透性主要由大孔径连通孔隙空间决定[21-22];在一定的温度、驱动压差条件下,较细小孔喉的孔隙空间可能不参与渗流,为简化渗流分析,在渗流模型中不考虑不参与渗流这部分孔隙空间,对参与渗流的孔隙空间利用毛细管模型描述流体在岩石中的渗流情况。设岩石截面积和长度分别为A和L,毛细管截面半径为rm、长度为lm[见图1(a)],在两相渗流(含水饱和度为Sw)情况下,水相渗流(导电)通道仍保持等截面积毛细管形状,水相实际渗流截面半径和长度分别为rw、lw[见图1(b)]。

图1 岩石渗流模型截面图

由渗流模型条件可知,岩石含水饱和度Sw可表示为

(1)

当岩石含水饱和度Sw=100%时,由泊肃叶定律可得

(2)

式中,Q为流体流量;Δp为压差;μ为水黏度。

由达西公式可得

(3)

式中,K为岩石含水饱和度Sw=100%时的渗透率,即绝对渗透率。联立式(2)、式(3)可得

(4)

同理可得到两相渗流(含水饱和度为Sw)时的水相渗透率

(5)

联立式(4)、式(5)可得到两相渗流(含水饱和度为Sw)时水相相对渗透率

(6)

式(6)可表示为

(7)

代入式(1),则式(7)可表示为

(8)

式中,lm/lw为含水饱和度为Sw时水相渗流长度与毛细管长度的比值。将式(8)变形为

(9)

(10)

式中,Swi为一定温度、驱动压差条件下的束缚水饱和度。

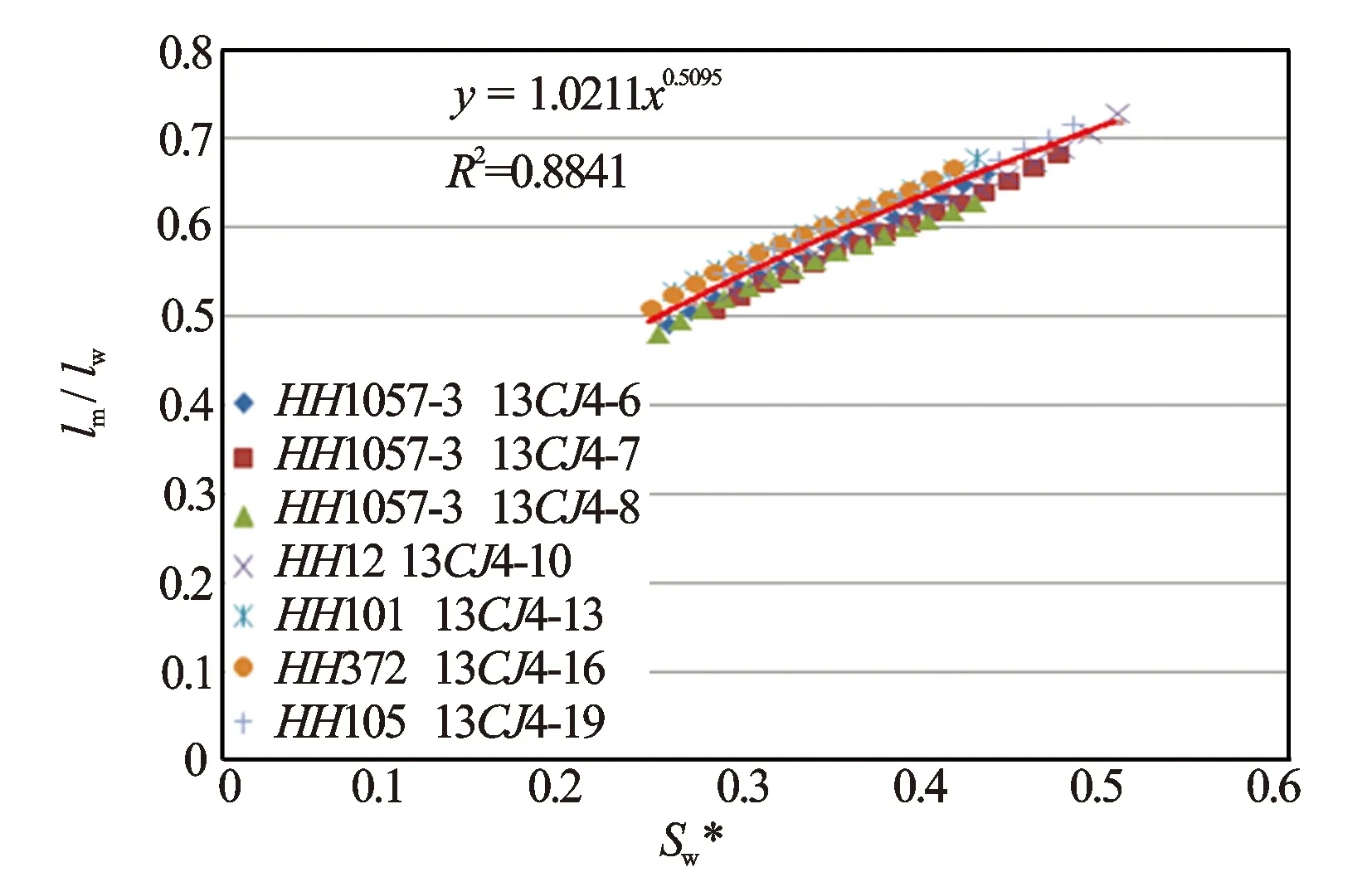
图2 lm/lw与关系图

(11)

由式(11),可用岩石含水饱和度与束缚水饱和度描述岩石不同含水饱和度时水相渗流路径长度比值,考虑到岩石中渗流与导电的相似性,可将式(11)引入到岩石导电模型分析。

2 纯岩石等效导电模型分析

建立纯岩石等效导电模型分析流体在岩石中的导电情况。假定岩石骨架不导电,岩石截面积和长度分别为A和L,为将岩石导电性与渗流特征联系起来,在一定的温度、驱动压差条件下,将岩石中的孔隙空间分为2部分:参与渗流的孔隙空间及不参与渗流的孔隙空间,均等效为等截面积毛细管束[见图3(a)]。其中参与渗流的孔隙空间等效为截面半径为rm、长度为lm的毛细管,即参与渗流的孔隙空间总体积与该毛细管孔隙体积相等,渗流(导电)路径平均长度与毛细管长度相等,导电能力也与毛细管相同;将不参与渗流的孔隙空间等效为截面半径为ri、长度为li的毛细管。在两相渗流(含水饱和度为Sw)情况下,水相渗流(导电)通道仍保持等截面积毛细管形状,参与渗流孔隙空间等效的毛细管中,水相实际渗流(导电)截面半径和长度分别为rw、lw[见图3(b)]。

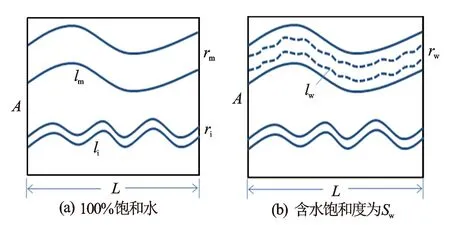
图3 岩石导电模型截面图

由模型条件可知,岩石含水饱和度Sw可表示为

(12)

岩石在给定温度、驱动压差条件下的束缚水饱和度Swi可表示为

(13)

由电阻率增大系数的定义可得岩石含水饱和度为Sw时电阻率增大系数可表示为

(14)

式中,Rt、σt分别为岩石含水饱和度为Sw时的电阻率、电导率;R0、σ0分别为岩石100%饱和水时的电阻率、电导率。根据电阻并联原理有

(15)

式中,σw为岩石中饱和的水的电阻率,进一步可得

(16)

同理可得岩石含水饱和度为Sw时的电导率

(17)

将式(16)、式(17)代入式(14),整理可得

(18)

令cim=li/lm,cwm=lw/lm,则

(19)

(20)

(21)

将式(20)、式(21)代入式(19),得

(22)

引入由相渗分析得到的式(11),可知

(23)

将式(23)代入式(22),整理,可得

(24)

式(24)即为岩石含水饱和度为Sw时的岩石电阻率增大系数I表达式,在导电模型中基于渗流特征差异对导电孔隙空间进行划分。将此公式暂命名为差异渗流导电公式。

3 差异渗流导电公式分析及其与阿尔奇公式关系

差异渗流导电公式右边包括3个量:含水饱和度Sw、束缚水饱和度Swi、岩石不参与渗流的孔隙空间平均导电路径长度与参与渗流的孔隙空间平均渗流(导电)路径长度之比cim(cim也可理解为不参与渗流的孔隙空间与参与渗流的孔隙空间平均迂曲度之比)。在一定的温度、驱动压差条件下,岩石束缚水饱和度Swi可视为常量,取值范围在0～1;cim也可视为常量,其值应大于1。

在理想情况下,岩石中所有的孔隙空间均参与渗流,即束缚水饱和度Swi=0,则式(24)表示为

(25)

即为阿尔奇公式(参数b=1,n=2)。

在实际岩石中,束缚水饱和度Swi≠0,岩石中含水饱和度Sw介于1～Swi,此时依据差异渗流导电公式得到的I—Sw关系示意图如图4。当Sw=1(即岩石100%饱和水,纯水层)时,电阻率增大系数值最小,I=1;当Sw=Swi(即岩石中无可动水,纯油气层)时,电阻率增大系数值最大,I=[Swi+cim2(1-Swi)]/Swi。由图4,在双对数坐标下,I—Sw关系呈现曲线关系,当从1向左逐渐减小时,曲线斜率逐渐减小。值得注意的是,当Sw较大(见图4曲线右端)时,I—Sw关系近似线性,其斜率即可理解为岩电实验中通常拟合的阿尔奇公式n值;而当Sw较小、接近Swi(图4曲线左端)时,I—Sw关系明显偏离右端的线性关系,电阻率增大系数I值明显向下偏转。阿尔奇公式所阐述的在双对数坐标下,纯净砂岩电阻率增大系数与含水饱和度呈线性关系,仅在I—Sw关系趋势线右端近似成立,在Sw接近Swi时并不成立。利用实测岩电实验数据对差异渗流导电公式进行检验,由岩电实验得到的电阻率增大系数、含水饱和度数据,拟合式(24)中的cim、Swi,依据式(24)绘制I—Sw关系趋势线,将趋势线与实测数据比较,发现差异渗流导电公式呈现的I—Sw曲线关系与实测岩电实验数据有很好的一致性。如图5所示,为鄂尔多斯盆地南部油区两块致密砂岩岩样岩电实验数据与差异渗流导电公式呈现的I—Sw关系趋势线对比图,两者吻合极好,验证了差异渗流导电公式对岩电实验中的非阿尔奇现象的描述能力。

图4 差异渗流导电公式I—Sw交会图

图5 实测岩电数据检验与差异渗流导电公式呈现的I—Sw关系趋势线对比图

通过差异渗流导电公式分析Swi和cim对I—Sw关系的影响。将cim固定(取cim=1.5),将Swi在0.1～0.5之间变化,I—Sw关系如图6所示。由图6,在双对数坐标下,不同Swi对应的I—Sw关系在呈现近似直线的部分(趋势线右端)斜率接近,即在保持cim不变的条件下,Swi的变化对岩电实验数据拟合的阿尔奇公式n值影响不大。可理解为,对2个岩石样品,如果非渗流孔隙空间平均迂曲度相同,其中1个有更多的相同迂曲度的非渗流孔隙空间(即束缚水饱和度相对较大),利用两者岩电实验中在双对数坐标下近似呈直线的实验数据拟合得到的阿尔奇公式n值应差别不大。

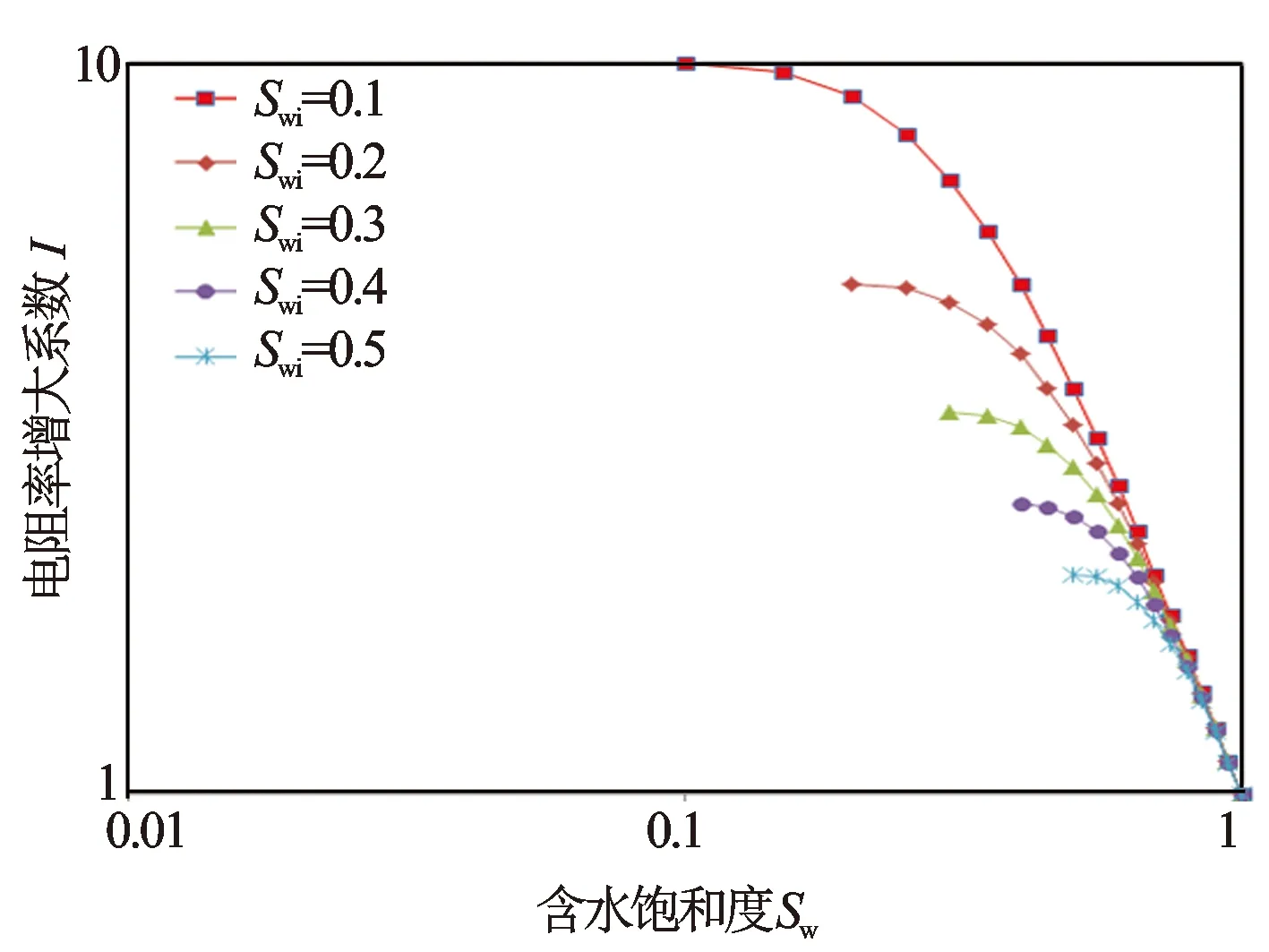
图6 不同Swi时I—Sw关系(cim=1.5)

将Swi固定(取Swi=0.3),将cim在1.2～3之间变化,I—Sw关系如图7所示。由图7,在双对数坐标下,不同cim对应的I—Sw关系在近似直线的部分斜率有明显差异,cim越大,斜率越大,即Swi不变的条件下,cim的变化对岩电实验数据拟合的阿尔奇公式n值有明显影响。可理解为,对2个岩石样品,如果束缚水饱和度相同,其中1个非渗流孔隙空间与渗流孔隙空间迂曲度之比更大(即cim更大),则其根据岩电实验数据拟合的阿尔奇公式n值更大。

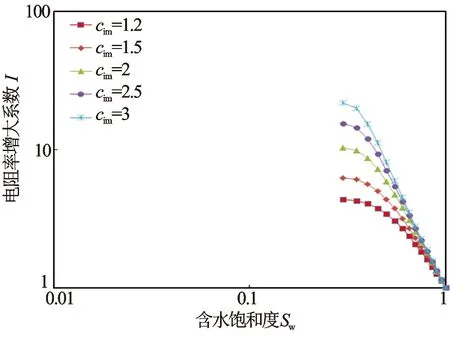
图7 不同cim时I—Sw关系(Swi=0.3)

4 结 论

(1) 利用毛细管模型描述流体在岩石中的渗流情况,通过渗流模型分析、公式推导和渗流实验数据,得到不同含水饱和度条件下水相渗流路径长度比值与岩石含水饱和度、束缚水饱和度关系式。

(2) 建立纯岩石等效导电模型,将纯岩石孔隙空间划分为参与渗流的孔隙空间与不参与渗流的孔隙空间,两部分并联导电。分析导电模型,引入渗流模型结论,推导出电阻率增大系数与含水饱和度的关系式,即差异渗流导电公式。

(3) 基于差异渗流导电公式,岩石电阻率增大系数由3个参数决定:含水饱和度、束缚水饱和度、不参与渗流的孔隙空间与参与渗流的孔隙空间平均迂曲度之比。当束缚水饱和度为0时,该公式退化为经典阿尔奇公式;当束缚水饱和度不为0时,双对数坐标下基于该公式的电阻率增大系数与含水饱和度关系在含水饱和度较大时呈现近似线性(类似阿尔奇公式规律),在含水饱和度较小则接近束缚水饱和度时则明显偏转,与岩电实验中常见的非阿尔奇现象相印证。

(4) 差异渗流导电公式解释了岩电实验中I—Sw关系的非阿尔奇现象,但该公式现在还无法应用于测井解释,原因在于公式中的渗流孔隙空间平均迂曲度与非渗流孔隙空间平均迂曲度之比还没有合适的实验手段可以测量,更谈不上用测井特征描述或计算它;但该公式有助于明确阿尔奇公式参数的影响因素,更好地理解阿尔奇公式的适用条件,从而在测井解释中更有效地应用阿尔奇公式。

参考文献:

[1] Archie G E. The Electrical Resistivity Log as an Aid in Determining Some Reservoir Characteristics [J]. AIME Petroleum Tech, 1942, 5(1): 1-8.

[2] 谭廷栋. 浅析阿尔奇公式 [J]. 国外测井技术, 1992, 7(2): 105-113.

[3] 孙建国. 阿尔奇(Archie)公式: 提出背景与早期争论 [J]. 地球物理学进展, 2007, 22(2): 472-486.

[4] 孙建孟, 王永刚. 地球物理资料综合应用 [M]. 东营: 中国石油大学出版社, 2001.

[5] 洪有密. 测井原理与综合解释 [M]. 东营: 中国石油大学出版社, 1993.

[6] 雍世和, 张超谟. 测井数据处理与综合解释 [M]. 东营: 中国石油大学出版社, 2007.

[7] 李秋实, 周荣安, 张金功. 阿尔奇公式与储层孔隙结构的关系 [J]. 石油与天然气地质, 2002, 23(4): 364-367.

[8] 么丽娜. 大庆长垣低孔渗砂岩储层原始含油饱和度模型研究 [D]. 大庆: 东北石油大学, 2012.

[9] 李霞, 赵文智, 周灿灿. 低孔低渗碎屑岩储集层双孔隙饱和度模型 [J]. 石油勘探与开发, 2012, 39(1): 82-91.

[10] 郑庆林, 王钰森, 赵雨. 低孔隙度条件下阿尔奇含水饱和度解释模型改进 [J]. 测井技术, 2006, 30(1): 57-59.

[11] 樊云峰. 鄂尔多斯盆地志丹-子北油区长6-1储层岩电关系特征研究 [D]. 西安: 西北大学, 2012.

[12] 张明禄, 石玉江. 复杂孔隙结构砂岩储层岩电参数研究 [J]. 测井技术, 2005, 29(5): 446-448.

[13] 陈杰. 基于电阻率测井资料研究致密砂岩孔隙结构特征 [D]. 成都: 西南石油学院, 2005.

[14] 李霞, 石玉江, 王林, 等. 致密砂岩气层测井识别与评价技术——以苏里格气田为例 [J]. 天然气地球科学, 2013, 24(1): 62-68.

[15] 岳文正, 陶果, 朱克勤. 饱和多相流体岩石电性的格子气模拟 [J]. 地球物理学报, 2004, 47(5): 905-910.

[16] Burdine N T. Relative Permeability Calculations from Pore Size Distribution Data [J]. Journal of Petroleum Technology, 1953, 5(3): 71-78.

[17] Pirson S J, Boatman E M. Prediction of Relative Permeability Characteristics of Intergranular Reservoir Rocks from Electrical Resistivity Measurements [J]. Journal of Petroleum Technology, 1964, 16(5): 564-570.

[18] Li K. A New Method for Calculating Two-phase Relative Permeability From Resistivity Data in Porous Media [J]. Transport in Porous Media, 2008, 74(1): 21-33.

[19] Li K. Interrelationship Between Resistivity Index, Capillary Pressure and Relative Permeability [J]. Transport in Porous Media, 2011, 88(3): 385-398.

[20] 黄蓬刚. 低渗透砂岩储层岩石渗流电性特征研究 [D]. 西安: 西安石油大学, 2012.

[21] 刘忠华, 吴淑琴, 杜宝会, 等. 储层渗透性与地层因素关系的实验研究与分析 [J]. 地球物理学报, 2013, 56(6): 2088-2097.

[22] 任晓娟. 低渗砂岩储层孔隙结构与流体微观渗流特征研究 [D]. 西安: 西北大学, 2006.