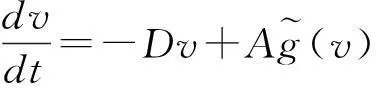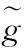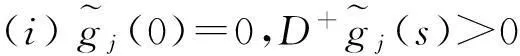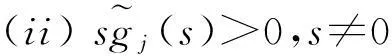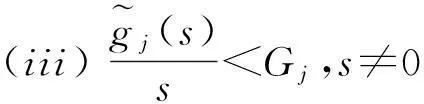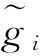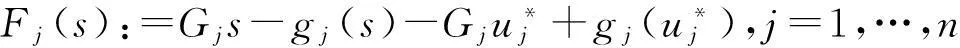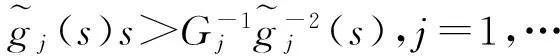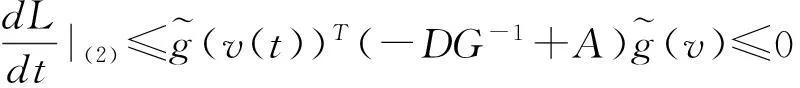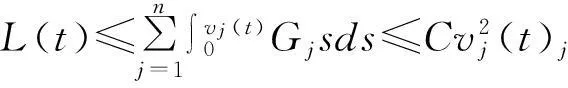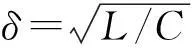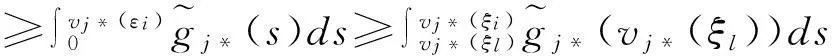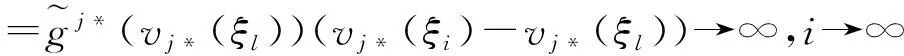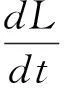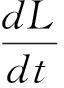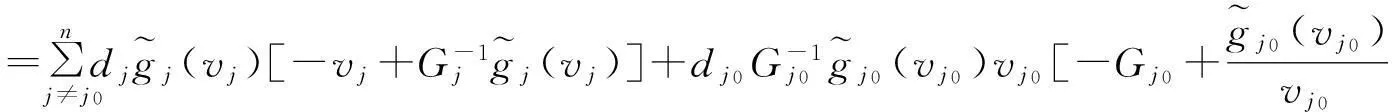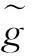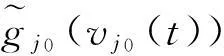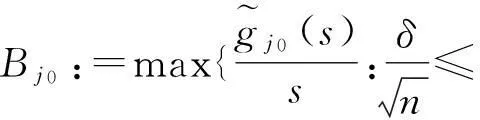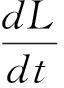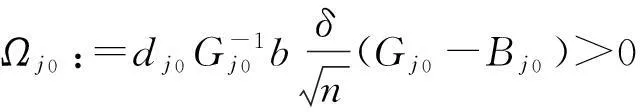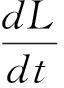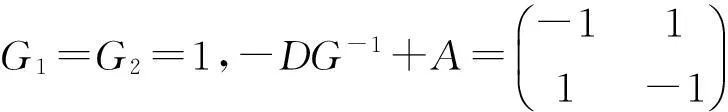Hopfield神经网络模型全局稳定的弱条件

宿　娟

(成都师范学院 数学系，四川 成都　610044)



Hopfield神经网络模型全局稳定的弱条件

宿娟

(成都师范学院 数学系，四川 成都610044)

摘要：研究了Hopfield神经网络模型全局渐近稳定的弱条件.模型中的激活函数没有有界和可微的限制，并且右上Dini导数可在多点取得最大值.首先构造Lyapunov函数，并利用可分析方法，证明了系数矩阵半负定是全局渐近稳定的弱条件.然后，通过例子和数值模拟说明了结论的有效性，改进了已有文献的结论.

关键词：神经网络；全局渐近稳定；半负定；平衡点

近年来神经网络在优化控制、模式识别等领域发挥了重要作用而备受关注[1-2].在众多的神经网络模型中，文[3]提出的Hopfield神经网络模型是目前研究和应用最为广泛的神经网络模型之一，用非线性微分方程描述如下：

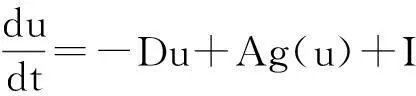
(1)

其中u:=(u1,…,un)T,uj表示第j个神经元的状态变量，T代表向量或矩阵的转置；D:=diag(d1,…,dn),对j=1,…,n，有dj>0，它表示网络在不连通且无外部附加电压差的情况下，第j个神经元恢复孤立静息状态的速率；A：=(aij)n×n是实对称方阵，aij表示第j个神经元对第i个神经元的影响强度；gj,j=1,…,n，是R上的连续函数，表示神经元的输出函数，也称为激活函数，而g(u):=(g1(u1),…,gn(un))T;I:=(I1,…,In)T,Ij∈R，j=1,…,n，表示外部输入.

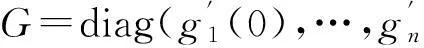
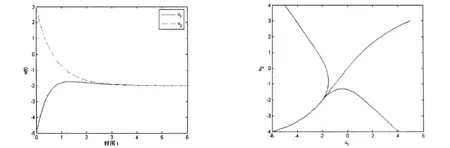
受文[7-9]的启发，本文将进一步削弱激活函数的要求至0

2结论和证明

假设u*是系统(1)的平衡点，令v=u-u*，则系统(1)改写成

(2)

文章假设激活函数gj,j=1,…,n，满足下列条件：

H10

引理1若条件H1，H2成立，对j=1,…,n，有

定义

(3)

从条件H1，H2得到

(4)

由(3)，(4)式有

(5)

再根据Fj的定义和(5)式有

引理1得证.

▯

定理1设系统(1)存在平衡点且条件H1，H2成立，若-DG-1+A半负定，其中G:=diag(G1,…,Gn)，则系统(1)的平衡点唯一且全局渐近稳定.

证明下面将证明分成三步完成.

步骤1构造Lyapunov函数，证明其导数非正，从而得到平衡点的稳定性.

构造Lyapunov函数

由引理1(i),(ii)易知L(t)正定，即L(t)≥0且L(t)=0当且仅当v(t)=0.

计算L(t)沿系统(2)的解曲线的导数有

(6)

由引理1(ii),(iii)有

(7)

将(7)式代入(6)式，并由-DG-1+A半负定可得

(8)

(9)

则L≥0.

步骤2，3将利用反证法证明极限L=0，由此说明v(t)=0的全局吸引性.

步骤2假设极限L≠0时估计v(t)的某个分量在t充分大时取值的范围.

假设L≠0，即

L>0.

(10)

下面寻找v(t)的某个分量在t充分大时的取值范围.由(8)-(10)式可得，存在t1满足

L(t)≥L,t≥t1.

(11)

利用引理1(ii),(iii)将L(t)放大有

(12)

‖v(t)‖≥δ,t≥t1.

(13)

(13)式说明对每个固定的t≥t1，存在与t相关的某个j0∈{1,…,n}.满足：

(14)

(14)式说明了对每个固定的t>t1，存在某个分量|Vj0(t)|，其下界为正.下面进一步寻找其上界.事实上存在常数M>0满足

|vj(t)|≤M,t≥t1,j=1,…,n.

(15)

若(15)式不成立，则存在序列{ξi}满足：(i)ξ1≥t1且{ξi}严格单增趋于+∞；(ii)存在v(t)的某一分量，设为vj*(t),满足vj*(ξi)→+∞或vj*(ξi)→-∞，i→∞.不妨设vj*(ξi)→+∞，则存在l∈N+满足vj*(ξi)>0，i≥l.由L(t)的定义和引理1有

与(9)式矛盾，因此(15)式成立.同理可证若vj*(ξi)→-∞时(15)式成立.

根据(14)，(15)式我们得出，对任意固定的t≥t1，存在某个j0满足

(16)

步骤3利用步骤2的结果来估计L(t)的取值，得出与L(t)正定的矛盾.

(17)

于是对固定的t≥t1,对(17)式中j≠j0的项利用引理1(iii)有

(18)

(19)

(16)式还进一步说明了

(20)

从而对固定的t≥t1，根据(16)，(18)和(19)式，我们得到

(21)

(22)

对(22)式两端在t1到t上积分有：

L(t)≤L(t1)-Ω(t-t1),t≥t1.

(23)

根据(23)式容易得到

L(t)<0,t→+∞，

即u*唯一且全局渐近稳定.定理得证.

▯

3数值模拟

本节将通过一个例子来验证所得结论.

例1考虑如下Hopfield神经网络模型，

其中激活函数

图1　初值为(-5，3)时的轨道收敛到(-2，-2)　　　　　　　　　图2　4条轨道皆收敛到(-2，-2)

注1例1中激活函数gi,i=1,2，其右上Dini导数D+gi(s)在s∈(-1,1)时均取得最大值1，用文[9]的结论不能判断该平衡点的全局稳定.

参考文献：

[1]ANTSAKLISP.Neuralnetworksincontrolsystem[J]. IEEE Control System Mag, 1990,10(3):3-5.

[2]CHEN Y H, FANG S C. Neurocomputing with time delay anlysis for solving convex quadratic programming problems[J]. IEEE Trans Neural Networks, 2000,11(1):230-240.

[3]HOPFIELD J J. Neurons with graded response have collective computational properties like those of two-stage neurons[J]. Proc Nat Acad Sci, 1984,81(10):3088-3092.

[4]PAJARES G, GUIJARRO M, RIBEIRO A. A hopfield neural network for combining classifiers applied to textured images[J]. Neural Networks, 2010,23:144-153.

[5]GHATEE M, NIKSIRAT M. A hopfield neural network applied to the fuzzy maximum cut problem under credibillty measure[J]. Information Sciences, 2013,229:77-93.

[6]CHENG Changyuan, LIN Kuanhui, SHIH Chihwen. Multistability and convergence in delayed neural networks[J]. Physica D, 2007,225:61-74.

[7]FORTI M. On global asymptotic stability of a class of nonlinear systems arising in neural network theory[J]. Journal of Differential Equations, 1994,113:246-264.

[8]LIU Xiwu, CHEN Tianping. A new result on the global convergence of Hopfield neural networks[J]. IEEE Trans Circuits Syst I, 2002,49(10):1514-1516.

[9]ZHANG Weinian. A weak condition of globally asymptotic stability for neural networks[J]. Applied Mathematics Letters, 2006,19:1210-1215.

[10]ZOU Lan, TANG Huajing, TAN K C, et al. Analysis of continuous attrractors for 2-D linear threshold neural networks[J]. IEEE Trans Neural Networks, 2009,20(1):175-180.

A Weak Condition for the Hopfield Neural Networks

SU Juan

(Department of Mathematics, Chengdu Normal University, Chengdu 610044, China)

Abstract:This paper studies the weak condition for the Hopfield neural networks whose activation functions may not be bounded or differentiable, and furthermore the upper right Dini derivatives of activation functions may obtain the maximum at more than one point. Firstly, by Lyapunov function and analysis methods, a weak condition of globally asymptotic stability is proposed. Then, example and numerical simulations are given to illustrate the theory developed in this paper. Our theory improves the existing results in the literature.

Key words:neural networks; globally asymptotic stability; nonpositive definite; equilibrium

中图分类号：O175.26

文献标志码：A

文章编号：1001-2443(2016)02-0115-05

作者简介：宿娟(1980-)，女，四川省崇州市人，讲师，硕士，研究方向为微分方程与动力系统.

基金项目：四川省教育厅项目(14ZB0329)；成都师范学院校级科研项目(CS15ZB04).

收稿日期：2015-05-10

DOI：10.14182/J.cnki.1001-2443.2016.02.003

引用格式：宿娟.Hopfield神经网络模型全局稳定的弱条件[J].安徽师范大学学报：自然科学版，2016，39(2)：115-119.