两种群都有非常数收获率的Holling-IV类捕食系统
2020-08-01 01:27王清娟吴燕林
洛阳师范学院学报 2020年8期
王清娟, 吴燕林
(阳光学院基础教研部, 福建福州 350015)
0 引言
国内外已有许多学者对具收获率或投放率的Holling-IV类捕食系统进行研究, 并取得很好的结论[1-5].但对于食饵具有较复杂的密度制约项, 两种群均有非常数收获率的研究相对较少, 文献[6-7]分别讨论了两种群都有非常数收获率的Holling-II类和Holling-III类模型, 研究了系统平衡点, 分析了中心焦点的阶数及其稳定性, 并给出系统极限环存在性及不存在性的相关条件.
文献[8]研究了如下系统:
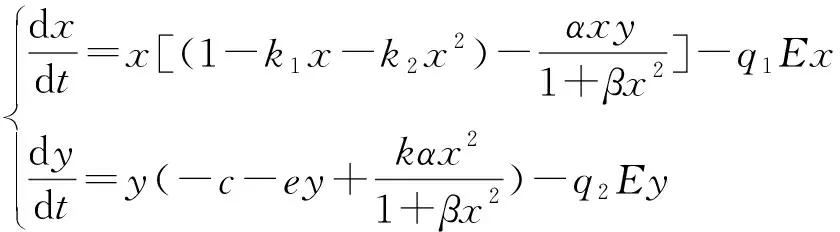
给出了此系统正平衡点全局稳定性的充分条件和生态解释.
在上述研究的基础上, 本文将讨论一类食饵种群具有非线性密度制约, 而捕食种群和食饵种群同时具有非常数收获率的Holling-IV类功能反应捕食系统:
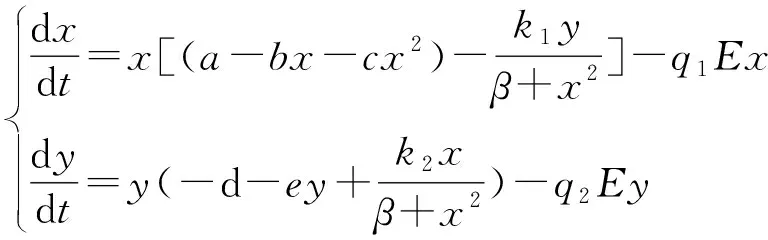
(1)
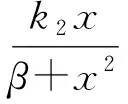
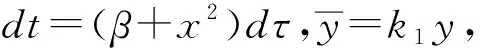
(2)
1 平衡点的存在与性态分析
系统(2)的平衡点有以下3种情况:
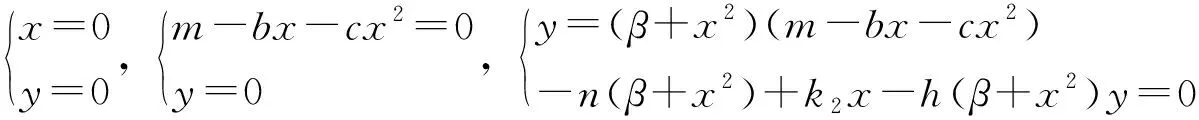
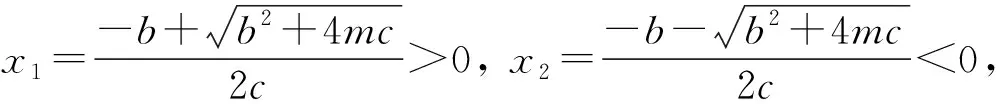
由以上讨论得, 系统有平凡平衡点(0,0), (x1,0), 而正平衡点的存在有3种情况: 无正平衡点、 有唯一正平衡点、 有两个平衡点. 下面只考虑系统在G={(x,y)|x≥0,y≥0}内有唯一正平衡点的情形.
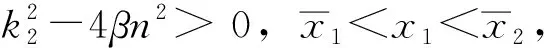
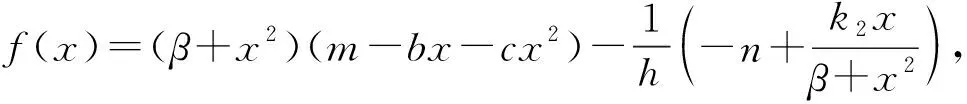

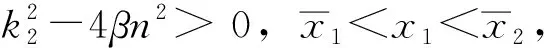
(1)平衡点(0,0)和(x1,0)为系统(1)的鞍点;
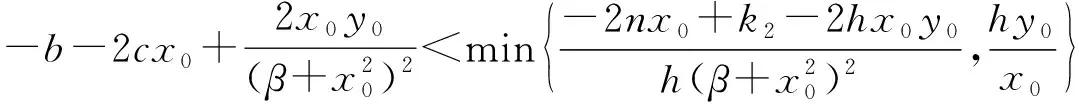
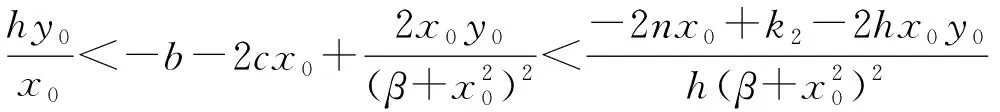
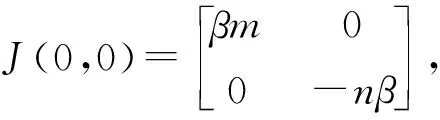
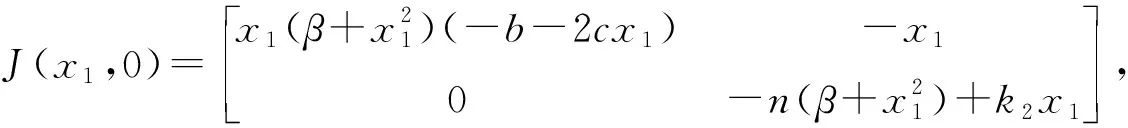
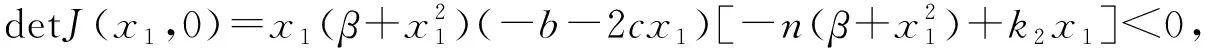
故平衡点(x1,0)为鞍点.
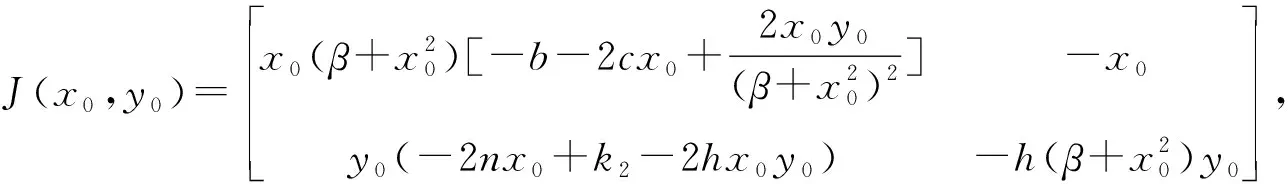
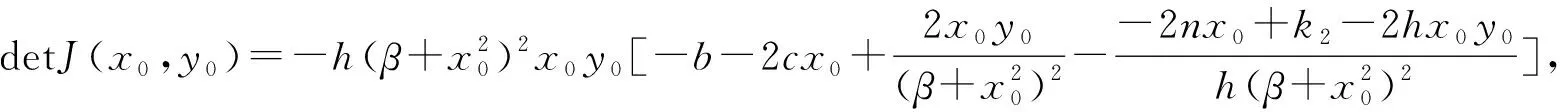
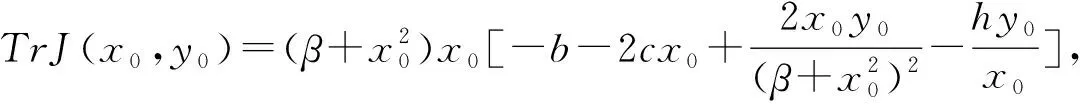
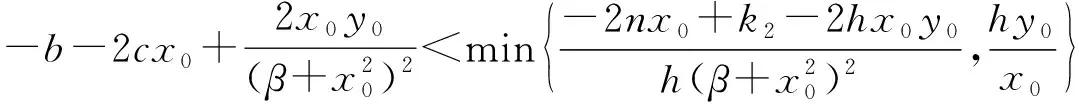
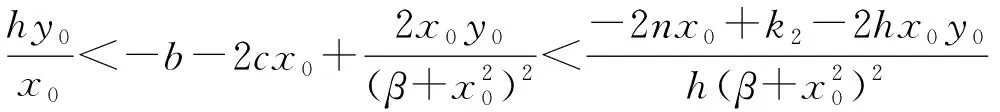
2 极限环的不存在性
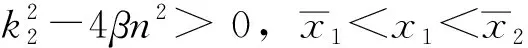
证明取Dulac函数B(x,y)=x-1y-1, 则
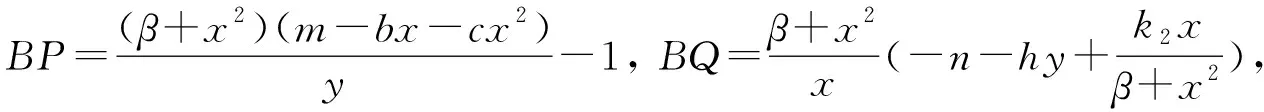
于是
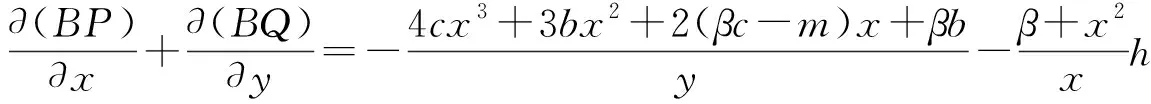
当βc-m>0时,
由Dulac判别法知: 系统(2)在G内无环.
猜你喜欢
湘潭大学自然科学学报(2022年1期)2022-04-11
数学物理学报(2022年1期)2022-03-16
应用数学(2020年4期)2020-12-28
成都工业学院学报(2019年3期)2019-11-06
数学物理学报(2019年4期)2019-10-10
数学物理学报(2019年3期)2019-07-23
烟台果树(2019年1期)2019-01-28
传媒评论(2018年7期)2018-09-18
上海师范大学学报·自然科学版(2018年3期)2018-05-14
经济数学(2017年4期)2018-01-18

