宝值(倍值)区间问题探究
2016-05-05 12:02王晓云,苏坤
高中数理化 2016年8期
宝值(倍值)区间问题探究
◇山东王晓云苏坤
近年高考中的函数题常出现以新定义为命题方向的信息型题目,给人以耳目一新的感觉,其中保值(倍值)区间问题具有一定的代表性.
保值(倍值)区间的定义:对于区间[a,b],若函数f(x)的定义域为[a,b]时,其值域也为[a,b],则称该区间为f(x)的保值区间;若x∈[a,b]时,其值域为[ka,kb](k∈N*),则称y=f(x)为“k倍值函数”,区间[a,b]为函数f(x)的“k倍值区间”.在具体的问题中,保值区间又有不同的表述形式,那么在解决具体的题目时,就要按照具体情况来分析.
1函数在定义域上单调递增





2函数在定义域上单调递减


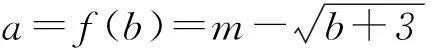
①

②
由式①、②得

③

④

⑤


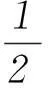

3函数在定义域上不具有单调性,在部分区间上具有单调性



图1
函数在x=0处无意义,故a、b同号.又函数值域为[0,+∞),[a,b]⊆[0,+∞),故a>0,所以0∉[a,b], 1∉[a,b],故有0 综上,不存在这样的保值区间. 4倍值区间问题 函数保值(倍值)区间问题的实质是函数“不动点”“稳定点”问题,因此首先考虑函数单调性,进而转化为对方程根的讨论,或者利用数形结合思想转化为函数图象的交点问题来解决,在解决具体问题中要灵活应用数学基本思想转化求解. (作者单位:山东省寿光市寿光中学)
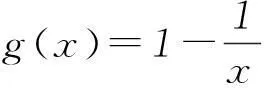






猜你喜欢
世界汽车(2022年3期)2022-05-23
语数外学习·高中版上旬(2022年2期)2022-04-09
新世纪智能(数学备考)(2021年9期)2021-11-24
新世纪智能(数学备考)(2020年9期)2021-01-04
数理化解题研究(2020年19期)2020-07-22
读写算(2019年5期)2019-09-01
中国外汇(2019年7期)2019-07-13
中国外汇(2019年6期)2019-07-13
中学生数理化·高一版(2018年10期)2018-11-08
理科考试研究·高中(2017年10期)2018-03-07

