“函数的单调性”复习设想
2016-05-05 12:03:22周爱飞
高中数理化 2016年8期
“函数的单调性”复习设想
◇江苏周爱飞
函数是高中数学重要章节,函数的单调性是其中的一个重要的概念,也是高考的热点问题.复习时要通过例题的设置引导学生充分理解、灵活运用概念,培养学生对单调性问题的转换能力.本文就“函数单调性”的考点复习进行分类突破,望能有助于高考复习实践.
1暴露学生常见错误

【设计意图】 将例1拿出来让学生自主探究,可以暴露出学生认知上最为常见的错误.
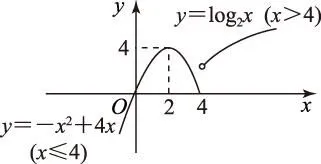
有学生会认为f(x)在(-∞,0)∪(0,+∞)上是单调减函数,实际上只要取x1=-1,x2=1,其中x1 2内化解决问题的方法 【设计意图】本例的解决方法可以运用定义法(略),也可以用复合函数法,相比较而言用后者方法更简单. 复合函数法设x2-2x-3=t,则y=log1/2t且t>0,所以x>3或x<-1.又t=(x-1)2-4,y=log1/2t关于t>0为减函数,求原来的函数单调递减区间,即求函数t=x2-2x-3>0的递增区间,所以原函数的单调递减区间为(3,+∞). 【设计意图】本例的解题方法可以运用定义法(略),也可以用导数法,相比较而言用后者更简单. 【设计意图】本例引导学生运用图象法,同时让学生有一种意识:有些函数较易画出草图,可用函数图象法辅助求解. 图象法作出函数f(x)的图象如图1所示: 图1 由图象可知f(x)在(a,a+1)上单调递增,需满足a≥4或a+1≤2,即a≤1或a≥4. (作者单位:江苏省江阴市华姿中等专业学校)


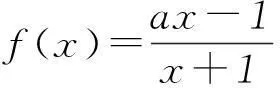


猜你喜欢
法律方法(2022年2期)2022-10-20 06:42:20
福建基础教育研究(2022年4期)2022-05-16 08:48:40
心电与循环(2021年4期)2021-11-29 02:41:56
湖南工业职业技术学院学报(2021年1期)2021-04-13 01:33:56
法律方法(2021年3期)2021-03-16 05:56:58
心电与循环(2020年3期)2020-06-18 13:43:12
时代青年·视点(2018年1期)2018-03-26 06:06:14
中国眼镜科技杂志(2016年17期)2016-10-24 08:36:30
文学教育(2016年18期)2016-02-28 02:34:53
湖南城市学院学报(自然科学版)(2016年4期)2016-02-27 14:02:46

