基于TOPSIS&Shapley值法的物流联盟利益分配研究

林　翊　王现兵

（福建师范大学，福建　福州　350117）



基于TOPSIS&Shapley值法的物流联盟利益分配研究

林翊王现兵

（福建师范大学，福建福州350117）

摘要：物流市场日益激烈的竞争促使物流企业倾向于采取联盟运营模式，而合理利益分配是物流联盟保持稳定的关键。在已有关于物流联盟研究的基础上，以物流企业的边际贡献度、风险、投资额、任务、服务能力为权重因子，采用TOPSIS法和Shapley值法结合方法为物流联盟构建优化的利益分配模型。并通过算例分析验证利益分配的合理性，以期为利益分配模型在物流联盟利益分配的运用及相关研究提供参考。

关键词：物流联盟；利益分配；TOPSIS法；Shapley值法

一、文献综述

物流企业为应对市场竞争及获取可持续经营，选择物流联盟运营模式较为普遍。物流联盟是企业之间以物流服务为合作基础的战略联盟，借助物流联盟，物流企业能够在交易费用、协同效应等角度获取竞争优势[1]。然而，物流联盟与其他类型联盟一样，也面临不稳定性威胁。Lunnan、Haugland以资源基础理论为研究背景，指出约有30％～70％的战略联盟会提前解体[2]。另外，也有学者指出物流企业形成物流联盟体的直接动力是获取更多经济利益[3]。因此，合理选取影响物流联盟稳定的利益分配因素，并据此选用恰当利益分配方法为物流联盟搭建公平、合理的利益分配模型具有重要意义。

当前，已有学者从多角度研究物流联盟的影响因素以及利益分配。其中，在联盟稳定性研究上，魏玮运用博弈论框架分析战略联盟组织不稳定原因，揭示了战略联盟稳定的关键在于组织内成员的博弈支付结构和博弈者对未来的预期[4]。杜义飞、李仕明、陈德富等认为参与者对价值创造的贡献直接影响联盟的稳定性，且价值创造的特征函数结构同联盟创造的最小价值之间存在线性变换关系[5]。徐扬、申金升、王传涛从经济学和系统学角度对物流企业风险厌恶程度、联盟协同效应以及各种成本系数等物流联盟稳定性影响因素进行分析，指出独立经营成本系数和合作成本系数对物流企业的联盟[6]。江琳琳采用BP神经网络方法对物流联盟中存在的风险进行研究，指出物流联盟存在关系风险和绩效风险，并进一步细分11个二级风险指标[7]。

在物流联盟利益分配研究上，靳慧斌、刘明广介绍基于全因素评价的利润分配机制，并指出全因素包括企业特质、实际贡献、努力程度、承担风险以及动态运营等[8]。马小龙提出动态物流联盟利益分配应遵循多劳多得、风险补偿、效用最大化和综合优化等四项原则[9]。甘家华、王建伟、陈卓等构建混合模式下的中小物流企业联盟收益分配模型，并认为联盟收益分配受可分配收益、承担物流任务数量、任务完成质量、投资额、联盟损失等几大主要因素影响[10]。在具体的联盟利益分配方法上，易欣、张飞涟、邱慧等指出，Shapley值法下的联盟利益分配不仅体现了每个联盟成员对该联盟的平均贡献，而且反映出个人在集体中的重要性，分配原理和分配结果容易被各个联盟成员视为公平[11]；而Shapley主要依据联盟成员的边际贡献为依据进行分配，随着联盟合作的深化，成员之间的联盟地位差距逐步缩小，物流成员为联盟运营所做出的其他努力因素对利益分配的影响日益增大。因此，李靓、刘征驰、周堂从投资额、风险承担等角度对基于贡献度的Shapley值法利益分配模型进行了修正，以此搭建基于风险和贡献度的联盟利益分配模型[12]。也有研究应用TOPSIS法对综合利益分配进行了分析，例如杨晶、江可申、邸强在联盟利益的综合分配研究中，利用TOPSIS为基于负理想点、基于正理想点、Shapley值法等所构建的利益分配方案赋予权重，以确定综合因素下的协调性联盟利益分配模型[13]；顾桂兰在协同利益分配的研究中，为避免利益分配的单因素性，利用TOPSIS法对基于投入、贡献、风险的三种利益分配赋予合理权重，构建体现协调性的利益分配模型，并通过算例验证了利益分配模型的合理性[14]。

综上所述，研究拟运用Shapley值法依据联盟成员边际贡献度为物流联盟构建体现边际贡献的利益分配模型。另外，为兼顾物流企业为构建联盟所承担风险、投资额、任务量等相关努力因素，在分析物流联盟利益分配具体影响因素基础上，研究运用具备运算简单、结果合理等特征的TOPSIS定权函数法对除边际贡献度外的其他相关利益分配影响指标进行归纳，以确定物流联盟成员的利益分配权重。并通过将两种利益分配模型进行结合，为物流联盟构建体现综合评价的利益分配。

二、物流联盟利益分配影响因素分析

物流企业参与构建物流联盟主要以应对市场竞争、获取可持续经营，即为获取比独立经营多的利益为目的，利益分配模型对物流联盟稳定性具有重要影响。为合理确定物流联盟的利益分配权重指标，根据物流企业自身经营特征，将物流联盟利益分配影响因素归类为边际贡献度、投资额、承担风险、任务承担、物流服务能力五个方面。其中，边际贡献度主要与物流企业的营业收入、市场占有率等经营业绩相关，也是物流联盟利益分配的主要影响因素之一。因此本文主要对投资额、承担风险、任务承担、物流服务能力四项指标体系进行分析。

（一）投资额

物流企业是以提供运输、配送、仓储、流通加工等服务的企业，以资源密集型服务为特征。因此，物流企业联合构建物流联盟的投资主要以有形资产投入为主，无形资产投入为辅。其中，有形资产投入包括仓库、车辆、建筑、设备等固定资产以及投入融资资金、人力资源等相关要素；无形资产则包括客户关系、市场竞争力、企业知名度等相关隐性资产。在物流联盟的利益分配中，成员投资额是重要的决定因素之一。

（二）承担风险

风险是物流联盟利益分配的重要影响因素，也是物流联盟利益分配的重要影响因素。根据风险来源，将物流联盟成员承担的风险种类分为内部风险和外部风险。其中，内部风险是来自物流联盟内部的各种威胁，一般包括物流协同服务形成的物流作业风险、信息传递风险、物流协调风险、个体利益诱因下的搭便车行为风险、控制与反控制风险等。外部风险是物流联盟以及物流成员经营所面对的外部冲击，主要包括政治、经济、技术、社会等方面。在对联盟成员承担风险的评价过程中，既要考虑成员承担的物流联盟风险，也要考虑物流企业在参与联盟体前后的风险承担能力以及风险变化。

（三）任务承担

物流企业组建联盟的本质是通过协同物流服务实现盈利，任务承担量是联盟利益分配的重要依据。根据资源基础理论，由于物流成员服务能力的差异，才有构建物流联盟体的必要性。因此，在联盟体制下，物流企业成员承担的任务性质以及数量有所不同，物流联盟的利益分配要体现任务承担因素的影响。在评价物流企业任务承担量过程中，不仅要考虑物流企业的任务承担量，同时要综合考虑承担任务类别，以公平、科学地确定任务承担权重因子。

（四）物流服务能力

提高物流服务效率以及满意度是物流企业构建联盟的主要目的之一，物流企业的物流服务能力也是联盟利益分配的重要影响因素。物流服务能力直接体现在物流服务质量上，主要包括企业职能服务质量和人力资源服务质量。其中，企业职能服务质量主要包括货物运输效率、物流服务时效、财务控制效率、成本控制效率等指标。人力资源服务质量主要指信息服务效率、工作效率、客户服务满意度等相关指标。

在构建物流联盟利益分配模型中，以Shapley值法分析物流联盟成员的贡献度，运用TOPSIS法对物流联盟下的其他多指标进行综合评价。因此，为合理地对物流联盟利益分配影响因素进行综合评价，本文将以Shapley值法下的利益分配模型反映物流企业的边际贡献度，通过TOPSIS法对承担风险、投资额、任务量、物流服务能力等四项因素进行综合评价，以确定物流联盟的利益分配系数。最后对两种利益分配方法下的利益分配确定相应权重，以确定各项指标综合评价下的物流联盟利益分配模型。

三、TOPSIS&Shapley值法的利益分配模型

（一）Shapley值法

Shapley值法是由Shapley L.S提出用以解决多人合作博弈问题的数学方法，是一种考虑联盟内部成员博弈的利益分配方法，其原理是根据联盟各成员为联盟体带来的利益增加值，以边际贡献为依据进行联盟利益分配[15]。本研究运用此方法对n个物流企业组建物流联盟的合作利益进行分配，对Shapley值法有以下假设和定义[13]：

假设物流联盟体由n家物流企业组建，构建的联盟成员集合I={1，2，…，n}，且对于物流联盟集合I中的任一子集si，均有与之对应的实数函数v （si）。其中，对于实数函数v（si）有以下规定：

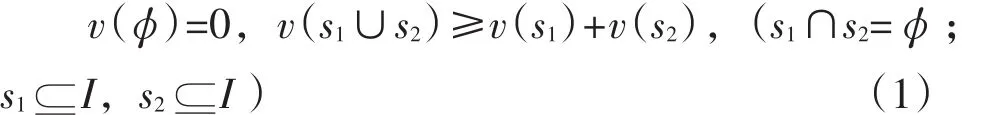
则称v（si）是满足I集合的对策函数。

假定xi为合作联盟I中联盟成员i所获取的最大利益分配额，则可得利益分配额组合数列x=（x1，x2，…，xn）。同时，假设v（i）表示联盟中的各成员独自经营获取的利益，则规定以上变量满足：

根据各变量满足的条件可知，联盟成员取得的利益分配额与联盟体的总利益额相等，即满足累加的性质；同时，联盟成员在联盟下取得的利益额高于独立经营取得利益额，即为满足合理性。设φi（v）表示在联盟I下，成员i获取的利益分配额，可得联盟下的利益分配集合为Φ（v）=[φ1（v），φ2（v），…，φn（v）]，则有：

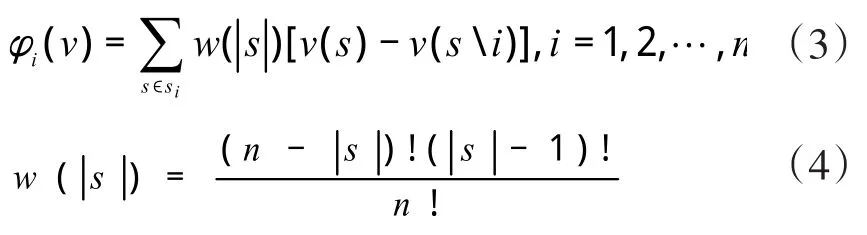
在（3）（4）式中，S表示联盟集合I可形成的所有子集。其中，|S|表示子集S中的成员个数，n为集合I中的成员个数。w（|s|）表示加权权重，v（s）表示在子集S所获取的利益额，v（si）表示子集S排除成员i所获取的利益额。

Shapley值法的联盟利益分配模型克服了利益平均分配问题，凸显个体成员在联盟中的重要性，且有利于激发成员积极性，但是Shapley值法也有一定缺陷。首先，假定联盟集合的各个子集组合是随机的，即为联盟成员地位相同的假设与现实情况不符；其次，假定联盟成员承担的风险均为1/n，难以反映实际联盟风险承担情况；最后，忽略了各个成员为组建联盟所做的其他贡献，比如投入资源、任务承担、服务质量等。而对于物流联盟来说，这些因素尤为重要。因此，为完善Shapley值法下的利益分配，为物流联盟构建更加合理的利益分配机制，本研究选取TOPSIS法对其修正。

（二）TOPSIS法

TOPSIS由Hwang和Yoon于1981年首次提出，是一种多变量、多目标的决策方法，通过测度备选方案的逼近理想解距离，实现对各方案优劣排序，已被广泛用于各个决策领域，其核心思想是根据求得的决策目标正理想解与负理想解来计算各方案的欧式距离，并得到各方案的相对贴近度；其中，相对贴近度越大的方案越优，据此实现对各个方案的优劣排序，此方法不仅具有计算简单、结果合理的优势，而且能够实现对多指标的定量评价[15]。因此，借助此方法能够可对物流联盟成员边际贡献度以外的其他指标进行评价，运用TOPSIS法有以下假设及步骤：

1.原始数据标准化处理。设物流联盟中有m个企业，选取n个一级评价指标，并假设xij为联盟成员在指标j上的所得评分，则有原始矩阵为A：

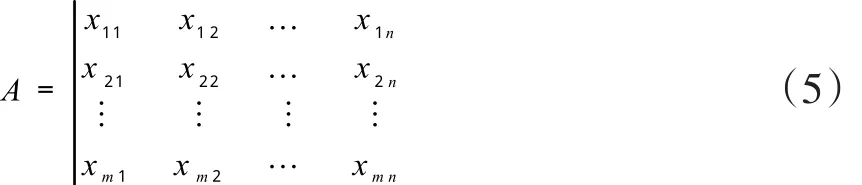
为实现对原始矩阵A的标准化处理，假设yij为标准化处理后的对应矩阵元素，并设标准化后的矩阵为B，则有：

2.正理想解与负理想解。根据确定的标准化矩阵B可得各家物流企业在相对应评价指标的正理想解yj+与负理想解yj-，并设y+、y-分别为正理想解数列与负理想解数列，有表达式：

3.欧式距离以及相对贴近度。利用（7）（8）所求得的正、负理想解，并假设联盟成员i的正欧式距离为Di+、负欧式距离为Di-、相对贴近度为Ci，则有：

根据（9）式计算的相对贴近度，可构建与各联盟成员相对应的相对贴进度数列，设为C，则有C={c1，c2，…，cn}。并将其标准化处理，则可得各联盟成员的权重因子数列β={μ1，μ2，…，μn}。最后可根据各联盟成员的权重因子确定其利益分配额，设为γi联盟成员i所分的利益，V（I）为整个联盟实现的利益额，有γi=μi·V（I）。

下面对可能影响矩形空心墩变形能力的参数进行敏感性分析，孙治国等通过有限元模拟，采用位移角作为延性目标对圆形空心墩的延性性能进行了研究。但国内对于桥梁结构而言，一般采用位移延性能力作为检验墩柱延性能力的指标。固本文采用位移延性能力作为延性指标，对纵筋配筋率、壁厚、轴压比及纵筋强度等参数对矩形空心墩抗震能力的影响。

（三）综合因子下的利益分配

在以上分析中，分别利用Shapley值法和TOPSIS法构建联盟利益分配模型。其中，Shapley值法主要关注联盟成员边际贡献度，确定其在联盟体中的重要性，以此计算联盟成员i的利益分配额为φi（I）。针对Shapley值法的缺陷，借助TOPSIS法对联盟成员除边际贡献度以外的、为构建联盟体所作努力的其他因素进行综合评价，以此确定各联盟成员的利益分配权重因子，并计算联盟成员i的利益分配额为γi。

根据Shapley值法和TOPSIS法下确定各联盟成员获取的利益分配额，为实现联盟成员为构建联盟所作努力的综合评价，假设Shapley值法下的利益分配权重为α，则有联盟成员i最终的利益分配额为：

四、算例分析

为验证所构建物流联盟利益分配模型的合理性，假设A、B、C三家物流企业组建物流联盟体，并设定各物流企业独立经营、任意两者结合经营以及三者构建物流联盟的利益额已知，通过Shapley值法与TOPSIS法对物流联盟利益分配进行分析。

（一）Shapley值法的利益分配

为确定不同合作机制下的物流企业贡献额，假设物流企业A单独经营能够获取利益20万，物流企业B独自经营能够获取利益30万，物流企业C独自经营能够获取利益40万。另假设，物流企业A、B联合运营能够获取利益80万；物流企业A、C联合运营能够获取利益90万；物流企业B、C联合运营能够获取利益120万；物流企业A、B、C组建物流联盟能够获取利益160万。根据Shapley值法下的联盟利益分配，物流企业A在不同联合运营模式下的相关利益统计数据见表1。

根据表1中的相关数据，并依据公式φ（iv）=，可求得在三家物流企业组建物流联盟下，物流企业A依据Shapley值法的利益分配模型获取的利益分配额为φ（Av）=36.67万。以此方法类求，可得物流企业B和物流企业C在物流联盟下的利益分配额分别为φ（Bv）=56.66万、φ（Cv）= 66.67万。根据求得的物流企业A、B、C在物流联盟下的利益分配额有φA（v）+φB（v）>v（A∪B）、φA（v）+φ（Cv）>v（A∪C）、φ（Cv）+φ（Bv）>v（B∪C），均满足Shapley值法下的利益分配条件。

（二）TOPSIS法的利益分配

通过Shapley值法对物流企业A、B、C的边际贡献度进行衡量，并以此确定三家物流企业在物流联盟下的利益分配额。为确定各物流企业在风险、投资额、任务量、服务能力等四个一级指标下的权重，通常情况是根据相关专家以及物流企业之间的协商确定，并利用TOPSIS法综合评价。

1.原始数据以及规范化处理。在风险承担的量化上以1～9数字为风险等级，数字越大风险越高；投资额按照各物流企业的实际情况核算、任务量主要依据物流企业的营业额确定；服务能力则主要依据物流企业的现代化管理水平、企业组织结构以及成本控制水平等确定。在本研究中，对物流企业A、B、C在四项指标的量化值假设见表2。

利用（5）式对原始数据进行规范化处理可得相关规范化矩阵B为：

表1　物流企业A基于Shapley值法的利益分配

表2　物流企业各指标原始数据

2.正理想解与负理想解。根据确定的标准化矩阵，可计算各个评价指标的下的正理想解y+与负理想解y－，有数列表达式为：

3.欧式距离以及相对贴近度。利用（11）求得的正、负理想解，以及利用公式（9）求得的物流企业A、B、C的正、负欧式距离和相对贴近度相关数据如表3所示。

表3　TOPSIS法的物流企业相关指标数据

根据表3数据，将物流企业A、B、C的相对贴近度规范化处理，可得三家物流企业联盟，以风险、投资额、任务量、服务能力等四项一级评价指标下的利益分配权重。设权重因子为μi，权重数列为β，则有β={μA，μB，μC}={0.23，0.32，0.45}。依据权重因子，可得在TOPSIS法下的物流企业所实现利益分配额为γ={γA，γB，γC}={35.8，51.2，72}。

（三）综合利益分配

在以上分析中，利用Shapley值法和TOPSIS法实现物流企业A、B、C搭建的联盟体下的利益分配。其中，Shapley值法侧重于分析三家物流企业的边际贡献度，而TOPSIS法对三家物流企业的风险、投资额、任务量、服务能力等指标进行评价。为实现联盟下的物流企业A、B、C的综合分析，以确定最终的联盟利益分配额，在本研究中，假设利用Shapley值法的利益分配权重为0.6，TOPSIS法下的利益分配权重为0.4，则根据公式（10），可得物流企业A、B、C构建联盟所实现的利益分配额分别为：

综上，利用Shapley值法与TOPSIS法结合的利益分配方法构建物流联盟的利益分配模型。且在算例分析中，假设有三家物流企业组建物流联盟以及相关变量假设，计算得出物流企业成员的利益分配额。

五、总结

合理、公平的利益分配是联盟保持稳定运营的基础，本文利用Shapley值法与TOPSIS法结合的方法为物流联盟搭建体现综合因素权重的利益分配模型。其中，Shapley值法体现物流企业成员的重要性，依据物流企业为联盟利益增值所做的边际贡献（营业额、利润额等指标体现）进行利益分配。另外，组建联盟的物流成员具有不同的属性，面临风险也不尽相同。因此，为实现物流联盟利益分配模型的优化，采用应用广泛、操作简便、结果可靠的TOPSIS综合评价方法对物流企业成员的风险、投资额、任务量、服务能力等四项关键指标进行综合评价，以此确定物流企业成员在联盟体制下的利益分配的权重因子。

另外，研究通过算例分析验证了所构建的物流联盟利益分配模型的可行性。结果显示，构建的物流联盟利益分配方法不仅克服了利益平均分配的不合理问题，而且将物流企业成员为搭建联盟的多个关键性努力因素纳入了联盟利益分配考虑之中，所计算出的利益分配结果具有合理性。构建的物流联盟利益分配模型更易被联盟成员所接受，有利于实现物流联盟的可持续运营。

参考文献:

［1］徐扬,申金升,王传涛.物流联盟的形成机理与协作博弈研究[J].交通运输系统工程与信息,2011(2).

［2］Lunnan R,Haugland S A.Predicting and Measuring Alliance Performance[J].Strategic Management Journal,2008(5).

［3］吴朗.产出分享模式下动态物流联盟利益分配方法[J].系统工程,2009(5).

［4］魏玮.战略联盟组织的稳定性、组织治理与信用约束机制[J].经济管理,2006(8).

［5］杜义飞,李仕明,陈德富.价值创造结构、K-重划分与联盟稳定性变化研究[J].管理工程学报,2012(1).

［6］徐扬,申金升,王传涛.物流联盟的形成机理与协作博弈研究[J].交通运输系统工程与信息,2011(2).

［7］江琳琳.基于BP神经网络的物流战略联盟风险评估研究[J].科技管理研究,2011(24).

［8］靳慧斌,刘明广.一种全因素的动态联盟利润分配机制设计[J].统计与决策,2007(20).

［9］马小龙.物流联盟内部利益分配问题的分析[J].交通科技与经济,2012(6).

［10］甘家华,王建伟,陈卓,等.质量导向下的中小物流企业联盟收益分配策略[J].技术经济与管理研究,2014(10).

［11］易欣,张飞涟,邱慧,等.不确定AHP和Shapley值应用于投标联合体利益分配[J].计算机工程与应用,2012(27).

［12］李靓,刘征驰,周堂.基于Shapley值修正算法的联盟企业利润分配策略研究[J].技术与创新管理,2009(6).

［13］杨晶,江可申,邸强.基于TO PSIS的动态联盟利益分配方法[J].系统工程,2008(10) .

［14］顾桂兰.基于TOPSIS的协同商务利益分配机制研究[J].企业经济,2011(3).

［15］谢识予.经济博弈论[M].上海:复旦大学出版社,2006.

［16］HWang C L,Yoon K S.Multiple Attribute Decision Making[M].Berlin: Spring-Verlag,1981.

作者简介：林翊（1973-），男，福建师范大学经济学院副教授，研究方向为产业组织与产业政策、企业管理。

基金项目：教育部人文社会科学青年基金项目“制造业与物流业联动发展的机理与模式研究——基于产业共生理论”（12YJC630220）

中图分类号：F224

文献标识码：A

文章编号：1672-3805(2016)01-0032-06

收稿日期：2016-01-13