损耗型单负材料双层结构的反射率及偏振度

康永强

(山西大同大学 固体物理研究所， 山西 大同 037009)



损耗型单负材料双层结构的反射率及偏振度

康永强*

(山西大同大学 固体物理研究所， 山西 大同 037009)

通过传输矩阵法，理论研究了损耗型单负材料双层结构在不同入射角时的反射率和偏振度。结果表明，损耗型单负材料双层结构不同于常规介电材料，随着入射角的增大，p分量反射率比s分量的反射率大。随着损耗(电损耗和磁损耗)的增大，p波的反射率和s波的反射率差异减小，直到重合，偏振度变为0。对于损耗型单负材料双层结构，当MNG层厚度增大时，偏振度变化幅度减小；而当ENG层厚度增大时，偏振度变化幅度增大。

反射率； 单负材料； 偏振度

1 引 言

近年来，含特异性材料的光子晶体引起了人们越来越多的关注[1-8]。目前研究较多的特异性材料有双负材料和单负材料[9-10]：介电常数和磁导率均为负数的材料被命名为双负材料，又称左手材料；介电常数和磁导率只有一个为负数的材料被命名为单负材料，其中包括负介电常数材料(ENG,ε<0，μ>0 )和负磁导率材料(MNG,ε>0，μ<0)。单负材料的折射率为虚数，通常是不透明的，仅支持倏逝波。然而，电单负材料和磁单负材料组成的双层匹配结构却存在共振隧穿现象[11-12]。在不考虑单负材料损耗时，将两种单负材料组成一维光子晶体结构，该结构中存在不同于常规布拉格带隙的零有效相位带隙[9,13-15]。该带隙受入射角、晶格涨落和入射波偏振模式的影响都比较小[14-17]。然而，在单负材料中，损耗是不可避免的[11-13,18]。同济大学研究小组报道了损耗型单负双层材料的非单调透射行为，即在某些情况下，增大耗散系数将会同时增大材料的透射性，这与损耗型介电材料的透射性质完全不同[18]。

本文研究了损耗型单负材料组成双层结构在不同入射角时的反射率和偏振度，以及损耗和单负材料双层结构厚度变化对反射率和偏振度的影响。结果表明，损耗型单负材料双层结构与损耗型介电材料的反射率和偏振度具有完全不同的性质。

2 理论模型及方法

设损耗型单负材料组成的双层结构AB沿z方向排列，其厚度分别为d1和d2。其中，A表示负介电常数材料，B表示负磁导率材料，周围是空气介质包围，其界面平行于x-y平面，如图1所示。

图1 负介电常数材料和负磁导率材料组成的双层结构，dA=11 mm,dB=42 mm。

Fig.1 Bilayer structure with negative permittivity material and negative permeability material,dA=11 mm,dB=42 mm.

损耗型单负材料的介电参数和磁导率通常取为Drud 模型[11-13]。负磁导率材料(μ<0，ε>0)表示为

(1)

负介电常数材料(ε<0，μ>0)表示为

(2)

其中，ωep=ωmp=10 GHz是电等离子频率和磁等离子频率，ω是角频率，γe、γm是电损耗因子和磁损耗因子。从式(1)和(2)可以看到，当ω在某一频率范围内时，μ1、ε2是负值，构成单负材料。

假定一单色平面波沿正z方向以入射角θ从空气入射到单负材料组成的双层结构AB，对于每一层，相应的传输矩阵[11-17]为

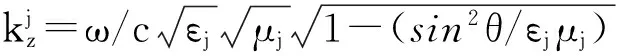
(4)

由传输矩阵得到反射系数为

(5)

则反射率R表示为

(6)

定义偏振度P为

(7)

其中，Rs为s波的反射率，Rp为p 波的反射率。

3 数值结果与讨论

材料的结构参数取为dA=11 mm、dB=42 mm, 频率f=1 GHz，图2给出了电损耗γe=0.8GHz保持不变，损耗型单负材料双层结构在4种不同磁损耗下的s波反射率Rs、p波反射率Rp及偏振度P随不同入射角θ的变化。其中图2(a)γm=0，图2 (b)γm=0.4GHz，图2(c)γm=0.6GHz，图2(d)γm=0.8GHz。从图2(a) 可以看到，正入射(θ=0°)时，s波反射率和p波反射率都为0.47，p波的反射率随着入射角的增大而增大，s波的反射率随着入射角的增大先减小后增大。并且发现除了入射角为0°和90°时，p波的反射率均大于s波反射率，这一点不同于常规损耗型介电材料(常规损耗型介电材料Rs>Rp)。偏振度P的最低点为-0.184，此时入射角对应于等效布儒斯特角(约70°)。从图2(b)可以看到，正入射时，p波反射率和s波反射率减小为0.26。随着磁损耗的增大，p波反射率和s波反射率进一步减小，图2(c)减小为0.2，图2(d)减小为0.18。进一步发现，随着磁损耗的增大，p波反射率和s波反射率逐渐趋于重合。所以可以得出结论，随着磁损耗的增大，p波反射率和s波反射率的差异减小，直到重合。即在高损耗的单负材料中，其反射波不受偏振度影响。

图2 在不同磁损耗下，两种单负材料组成的双层结构的s 波反射率Rs、p波反射率Rp及偏振度P随不同入射角θ的变化。(a)γm=0；(b)γm=0.4GHz；(c)γm=0.6GHz；(d)γm=0.8GHz。

Fig.2Rs,RpandPvs.θat diferent magnetic losses in ENG-MNG bilayer. (a)γm=0. (b)γm=0.4GHz. (c)γm=0.6GHz, (d)γm=0.8GHz.

图3 在不同电损耗下，两种单负材料组成的双层结构的s波反射率Rs、p波反射率Rp及偏振度P随不同入射角θ的变化。(a)γe=0；(b)γe=0.4GHz；(c)γe=0.6GHz；(d)γe=0.8GHz。

Fig.3Rs,RpandPvs.θat diferent electric losses in ENG-MNG bilayer. (a)γe=0. (b)γe=0.4GHz.(c)γe=0.6GHz. (d)γe=0.8GHz.

保持磁损耗γm=0.8GHz不变，单负材料双层结构在不同电损耗下的s波反射率Rs、p波反射率Rp及偏振度P随不同入射角θ的变化如图3所示。其中图3(a)γe=0，图3(b)γe=0.4GHz，图3(c)γe=0.6GHz，图3(d)γe=0.8GHz。从图3(a)同样可以看到，p波的反射率随着入射角的增大而增大，s波的反射率随着入射角的增大先减小后增大。同样发现，除了入射角为0°和90°时，p波的反射率均大于s波反射率，这一点性质与图2(a)中相同。而与图2(a)不同的是，图3(a)中偏振度P的变化幅度更大，偏振度的最低点为-0.542，此时入射角对应于等效布儒斯特角(约65°)。这主要是由于材料B的厚度大于材料A，磁损耗主要对材料B的反射率有影响。从图3(b)、(c)、(d)可以看到，随着电损耗的增大，p波反射率和s波反射率的差异减小，最后，p波反射率和s波反射率重合。这一性质也与图2中类似。

接着，我们研究损耗型单负材料双层结构厚度变化对反射率和偏振度的影响。先保持ENG材料厚度d1=11 mm 不变，电损耗和磁损耗γe=γm=0.4GHz，改变MNG材料厚度d2=6,11,21 mm。单负材料双层结构反射率和偏振度随不同入射角的变化如图4所示。从图4可以看到，厚度变化不影响Rp>Rs的性质。由图4(a)可知，在入射角θ<40°时，s波反射率Rs和p波反射率Rp都很小，表明此时损耗型单负双层结构有很大的透过率。随着入射角的增大，s波反射率Rs和p波反射率Rp都增大，即透过率降低。从图4(b)和图4(c)看到，随着MNG材料厚度d2的增大，偏振度P的变化幅度减小，偏振度P的最低点向右移动，对应的有效布儒斯特角增大。

最后，保持MNG材料厚度d2=16 mm 不变，改变ENG材料厚度d1=6,11,21 mm，电损耗和磁损耗γe=γm=0.4GHz，单负材料双层结构的反射率和偏振度随不同入射角的变化如图5所示。从图5可知，随着d1的增大，在正入射时，p波反射率Rp和s波反射率Rs逐渐变小，即透过率逐渐增大，但Rp>Rs的性质仍然保持不变。进一步发现，随着d1的增大，偏振度P的变化幅度增大，P的最低点向左移动，对应的有效布儒斯特角减小，与图4变化过程正好相反。

图4 d2=6(a), 11(b), 21(c) mm时，反射率和偏振度随入射角的变化。

图5 d1=6(a), 11(b), 21(c) mm时，反射率和偏振度随入射角的变化。

4 结 论

对损耗型单负材料组成双层结构的s波反射率、p波反射率和偏振度进行了研究。结果表明，该结构显著不同于常规损耗介电材料，性质是Rp>Rs。随着损耗(电损耗和磁损耗)的增大，s波反射率和p波反射率同时减小，偏振度变化幅度减小，最后，s波反射率和p波反射率重合，偏振度变为0。对于损耗型单负材料双层结构，当MNG层厚度增大时，偏振度变化幅度减小，偏振度P的最低点对应的有效布儒斯特角增大；而当ENG层厚度增大时，偏振度变化过程恰恰相反。

[1] PENDRY J B. Negative refraction makes a perfect lens [J].Phys.Rev.Lett., 2000, 85(18):3966-3969.

[2] SMITH D R, PADILLA W J, VIER D C,etal.. Composite medium with simultaneously negative permeability and permit [J].Phys.Rev.Lett., 2000, 84(18):4184-4187.

[3] ZHANG C M, GAO P, SUN M Z,etal.. Analysis of the resonant frequency of the octagonal split resonant rings with metal wires [J].Appl.Opt., 2010, 49(29):5638-5644.

[4] VESELAGO V G. The electrodynamics of substances with simultaneously negative values ofεandμ[J].Sov.Phys.Usp., 1968, 10(4):509-514.

[5] ZHANG S, FAN W J, MALLOY K J,etal.. Near-infrared double negative metamaterials [J].Opt.Express, 2005, 13(13):4922-4930.

[6] PENDRY J B, HOLDEN A J, STEWART W J,etal.. Extremely low frequency plasmons in metallic mesostructures [J].Phys.Rev.Lett., 1996, 76(25):4773-4766.

[7] 张检发,袁晓东,秦石乔. 可调太赫兹与光学超材料 [J]. 中国光学, 2014, 7(3):349-364. ZHANG J F, YUAN X D, QIN S Q. Tunable terahertz and optical metamaterials [J].Chin.Opt., 2014, 7(3):349-364. (in Chinese)

[8] QIAO F, ZHANG C, WAN J,etal.. Photonic quantum-well structures: multiple channeled filtering phenomena [J].Appl.Phys.Lett., 2000, 77(23):3698-3700.

[9] LIN M, OUYANG Z B, XU J,etal.. Omnidirectional and multi-channel filtering by photonic quantum wells with negative-index materials [J].Opt.Express, 2009, 17(7):5681-5866.

[10] FREDKIN D R, RON A. Effectively left-handed (negative index) composite material [J].Appl.Phys.Lett., 2002, 81(10):1753-1755.

[11] KANG Y Q, ZHANG C M, GAO P,etal.. Electromagnetic resonance tunneling in a single-negative sandwich structure [J].J.Mod.Opt., 2013, 60(13):1021-1026.

[12] 康永强,高鹏,刘红梅,等. 含各向异性左手材料的一维Thue-Mores准周期结构的反射带隙 [J]. 光子学报, 2015, 44(3):0319004-1-6. KANG Y Q, GAO P, LIU H M,etal.. Reflection band gap in Thue-Morse quasicrystal containing anisotropic left handed material [J].ActaPhoton.Sinicca, 2015, 44(3):0319004-1-6. (in Chinese)

[13] KANG Y Q, ZHANG C M, MU T K,etal.. Resonant modes and inter-well coupling in photonic double quantum well structures with single-negative materials [J].Opt.Commun., 2012, 285(24):4821-4824.

[14] JIANG H T, CHEN H, LI H Q,etal.. Properties of one-dimensional photonic crystals containing single-negative materials [J].Phys.Rev. E, 2004, 69(6):066607-1-5.

[15] WANG L G, CHEN H, ZHU S Y. Omnidirectional gap and defect mode of one-dimensional photonic crystals with single-negative materials [J].Phys.Rev. B, 2004, 70(24):245102-1-6.

[16] LI P N, LIU Y W. Multichannel filtering properties of photonic crystals consisting of single-negative materials [J].Phys.Lett. A, 2009, 373(21):1870-1873.

[17] CHEN Y H, DONG J W, WANG H Z. Omnidirectional resonance modes in photonic crystal heterostructures containing single-negative materials [J].J.Opt.Soc.Am. B, 2006, 23(10):2237-2240.

[18] DONG L J, DU G Q, JIANG H T,etal.. Transmission properties of lossy single-negative materials [J].J.Opt.Soc.Am. B, 2009, 26(5):1091-1096.

Reflectance and Degree of Polarization in Loss Single-negative Bilayer

KANG Yong-qiang*

(InstituteofSolidStatePhysics,ShanxiDatongUniversity,Datong037009,China)
*CorrespondingAuthor,E-mail:kyq_2000@sohu.com

The reflectance and degree of polarization in the loss single negative bilayer were investigated by transfer matrix method. It is found that the angle dependent reflectance of p waves is larger than that of s wave, which is contrary to the usual material with both positive epsilon and mu. With the increasing of loss (electric loss and magnetic loss), the difference ofRpandRsdecreases, and the polarization degree is 0. The increasing of the thickness of MNG layer makes the dip inPshallow, while the increasing of the thickness of ENG layer makes the dip inPdeep.

reflectance; single-negative material; polarization

康永强(1979-)，男，山西文水人，博士，讲师，2014年于西安交通大学获得博士学位，主要从事光子晶体、超材料方面的研究。

E-mai: kyq_2000@sohu.com

1000-7032(2016)03-0353-05

2015-11-22；

2015-12-17

国家自然科学基金( 61307002)； 博士科研启动基金(2014-B-04)资助项目

O431

A

10.3788/fgxb20163703.0353