浅水中低速斜航船舶水动力预报及验证与确认分析

邹璐

（上海交通大学 船舶海洋与建筑工程学院 高新船舶与深海开发装备协同创新中心，上海 200240）

浅水中低速斜航船舶水动力预报及验证与确认分析

邹璐

（上海交通大学 船舶海洋与建筑工程学院 高新船舶与深海开发装备协同创新中心，上海 200240）

浅水中的斜航船舶受到浅水阻塞效应和不对称流的综合影响。为预报该运动中的船舶水动力，文章采用基于定常雷诺平均纳维—斯托克斯方程的计算流体动力学方法，对浅水中做斜航运动的船舶粘性绕流场进行数值模拟。考虑低航速运动的特点，忽略航速影响下的自由面兴波，由数值计算得到水动力系数在漂角影响下的变化规律。针对计算精度问题，在数值模拟中从验证和确认角度分析和评估计算结果：通过网格收敛性分析分析数值误差与不确定度；结合试验数据考察计算模型的误差。此外，从计算区域尺度、湍流模型、边界条件、船体下沉和纵倾作用方面对模型误差的影响因素进行探讨，可为改进计算模型、提高数值模拟精度提供参考依据。

浅水；斜航运动；CFD；水动力系数；误差和不确定度；验证和确认

0 引 言

如何准确预报船舶操纵水动力一直以来是船舶操纵性研究领域的热点问题，因为这与船舶运动模拟和操纵控制密切相关。目前主要的预报方法包括：经验公式估算、约束模试验以及基于计算流体动力学（Computational Fluid Dynamics,CFD）的数值模拟。近年来，基于CFD的数值计算方法得到越来越广泛的应用，已成为与约束模试验并驾齐驱、相辅相成的一种水动力预报方法。然而，该方法不可避免地存在精度问题。对数值计算中的误差和不确定度的准确评估以保证数值模拟的可靠性是CFD数值预报的重要环节。目前验证和确认（Verification and Validation）是能有效评估数值和模型误差的方法，国际上有许多相关研究进展[1-5]。

实际工程中船舶常出现斜航运动的情况。此时，船体的纵轴线与航行方向成一定夹角，即所谓的漂角。船体因受到不对称流的影响，船尾出现较直航情况下愈加明显的流体分离，船尾伴流变大。在浅水中斜航的船舶由于受到阻塞效应和不对称流的综合作用，船体受到更复杂的水动力影响。浅水斜航船舶水动力预报在国际上是比较研究的代表案例。“船舶操纵预报方法验证与确认专题讨论会”SIMMAN2008[6]对此设置了相关基准算例。意大利船模水池INSEAN（Italian Ship Model Basin）对该算例进行了平面运动机构约束模试验（Planar Motion Mechanism，PMM），为数值模拟提供了重要的对比研究用数据。国外的Simonsen等[7]、Toxopeus等[8]和国内的田喜民等[9]、钱永峰[10]采用基于雷诺平均纳维—斯托克斯方程（Reynolds Averaged Navier-Stokes，RANS）的CFD方法均对浅水斜航问题做过相关研究，但这些研究并没有系统讨论计算中的误差和不确定度。作者前期工作[11]中已对浅水斜航有一定研究，本文主要是在验证和确认基础上更深入地探讨数值计算的精度水平、量化评估误差和不确定度，以及分析可能的误差源。

1 物理问题的描述

本文参考SIMMAN2008专题讨论会中的基准算例，选取浅水中在固定漂角下低速斜航运动的超大型油船船模KVLCC2（KRISO Very Large Crude-oil Carrier）为研究对象。图1表示的是KVLCC2斜航运动的示意图，β为漂角。本文着重考察的是纵向力X，横向力Y和转首力矩N，计算结果以无量纲形式表示为：

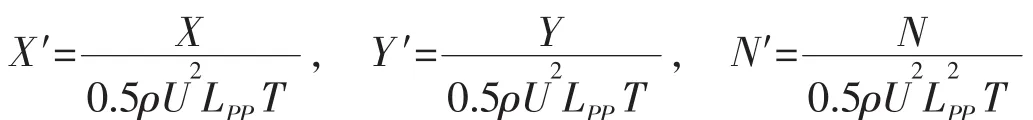
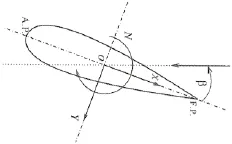
图1 斜航运动示意图Fig.1 Illustration of the drift motion

图2 KVLCC2船型及浅水域几何示意图Fig.2 Schematic of the flow field(h:water depth)

算例中船后不带附体（桨/舵）；船模缩尺比为45.714，对应主尺度：垂线间长LPP=7.0 m，船宽B= 1.269 m，吃水T=0.455 m。船型几何如图2所示。根据INSEAN的试验设置，计算中水深吃水比h/T= 1.2；低船速U=0.533 m/s，对应的雷诺数Re=U·LPP/ν=3.697×106，佛汝德数（ν为水的运动粘度，g为重力加速度）。此外，选取四个漂角β=0°，2°，4°，6°进行系列计算。由于航速较低，假定自由面兴波及船体自由下沉和纵倾对船舶水动力的影响可忽略不计，本文采用叠模方法模拟静水面并保持船体正浮。

2 数值方法

假定绕斜航KVLCC2船模的粘性流是不可压缩的，相应的流动问题可由如下控制方程描述：

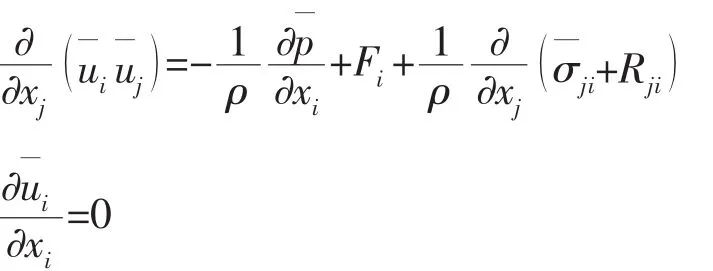
本文采用船舶水动力学专业软件SHIPFLOW中的RANS求解器XCHAP，对物理问题展开数值计算。XCHAP基于有限体积法，用Roe格式[12]离散对流项，中心差分离散扩散通量。离散的方程由交替方向隐格式（alternating direction implicit scheme）[13]求解。压力和速度通过人工压缩格式（artificial compressibility scheme）[14]全耦合。为封闭控制方程，XCHAP中主要有两个湍流模型可用：剪切应力输运模型（Shear Stress Transport k-ω model，k-ω SST）[15]和显式代数应力模型（Explicit Algebraic Stress Model，EASM）[16]。

3 计算设置和网格生成

数值计算中的坐标系定义为固定在船上的右手笛卡尔直角坐标系：坐标原点置于船中剖面、中纵剖面和水面的交点，如图3所示。x，y，z轴分别指向船首、右舷、船底。由于船体周围流场不对称，数值求解选取的计算区域包含整个船体，由七个边界面组成：船体表面；静水面（z=0）；浅水底的位置根据计算条件位于水面下1.2T处；计算域入口在船首柱（F.P）前的一倍船长LPP处；出口在船尾柱（A.P）后的LPP处；两边的计算域边界面（即岸壁处）距船中心线均为1.8LPP。在计算域的各个边界面上分别设置边界条件：船体表面满足无滑移条件（No-slip），无壁面函数；入口/出口边界面上设置入流/出流条件（Inflow/Outflow），即入口处流场速度等于船速，出口处除压力外的所有的流动参数法向梯度为零；水面处由于不考虑兴波影响，采用滑移条件（Slip）模拟为对称面；浅水底及岸壁同样设置滑移条件以简化计算。计算中首先采用EASM模型进行湍流模拟。

为保证数值求解中网格离散的质量，本文采用结构化重叠网格技术对计算域进行网格离散。由图4可见，重叠网格由两部分组成。首先对船体及其附近的区域用半圆柱型的H-O型贴体网格离散，在船首尾附近流场变化比较突出的区域加密网格以提高求解的精度。但是很明显这种网格形式不适合离散船身下方平直的浅水底，因而在H-O网格外部用嵌套的H-H网格来离散平直几何边界（特别是水面、岸壁和水底）附近的区域。

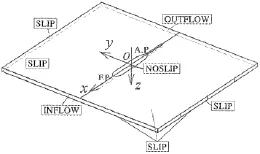
图3 坐标系及边界条件Fig.3 Manoeuvring coordinate system and boundary conditions

图4 网格离散示意图Fig.4 Schematic of grid distribution

4 验证和确认（Verification and Validation）

4.1 验证：数值误差和不确定度分析

验证（Verification）是用来评估数值误差和不确定度。数值求解过程中的误差由计算机的舍入误差、计算迭代误差和对数学方程的离散误差组成，其中占主导的部分为离散误差。离散误差的产生是源自数值求解需要对数学方程进行空间和时间上的离散。理论上随着离散点的增加，离散误差应该趋于零，然而实际数值计算中的离散误差很难避免，需要通过所谓的“收敛性分析（Convergence study）”来评估离散问题带来的误差和不确定度。对于定常问题，则主要在于网格收敛性分析。本文采用Eça等[4]的最小二乘（Least Squares Root，LSR）理论对一系列不同密度的网格进行分析和评估。

为具体考察本研究中的数值误差和不确定度，以h/T=1.2，β=4°的斜航运动为例进行网格收敛性分析。根据Eça等[4]的方法，网格收敛性分析需要通过加密网格来考察数值误差和不确定度。首先选定网格尺度比值（hi+1和hi为两相邻网格的步长），按照这个网格加密比例，生成6个密度不同的网格。表1列举了这6个网格密度下的网格节点数，其中以hi/h1表示网格尺度比以区别网格的疏密程度，h1对应的是最密的网格。然后，对这些系统加密的网格进行数值计算得到相应的水动力系数预报结果。

表1 网格尺度Tab.1 Dimensions of grid series

图5 X′，Y′，N′的网格收敛性Fig.5 Grid convergence of X′,Y′,N′

应用LSR方法对数值结果进行曲线拟合，得到网格收敛趋势图。网格5给出了各网格密度下的X′，Y′，N′数值计算结果和曲线拟合得到的网格收敛趋势及其相关参数（外推值S0，精度p），其中也给出了理论精度pth（在数值方法中已知，本文为二阶精度）对应的拟合结果用作比较。需要说明的是，网格6由于网格过于稀疏给出的结果不精确，因此其数值解没有包含在曲线拟合当中。由图5可见，拟合得到的精度p都大于理论的pth=2.0，特别是Y′，原因很可能是其各个数值解呈现一种分散（scatter）的形式，使得Y′值的变化与网格疏密程度无明显相关性。而X′和N′的结果图显示，随着网格的加密，二者的数值解都趋于收敛，相邻网格数值解之差也逐渐变小。

表2列出了由LSR方法得到的不确定度USN，其中选取最后加密的三个网格（网格3，网格2，网格1）的结果以作比较。由网格3到网格1，三个水动力系数的不确定度并不明显随网格密度变化，结合图5也可看到三个网格密度对应的数值解较为接近。然而表2中数值不确定度的值仍然较大，一方面是由于本研究中用到的重叠网格某种程度上将网格离散复杂化，因而使其数值求解精度受限；另一方面对本文中的p≫2.0情况，LSR方法的不确定度评估公式的准确度还有待考察。由网格收敛趋势图（图5）可知，高密度网格能给出较为精确的数值解，但同时也需要更多的计算资源。在结合数值不确定度结果并权衡数值精度和计算时间的基础上，下文选择对网格3的结果展开进一步讨论，并用该网格进行系统的浅水斜航计算以考察漂角对船舶水动力系数的影响。

表2 X′，Y′，N′的数值不确定度Tab.2 Numerical uncertainties of X′,Y′,N′

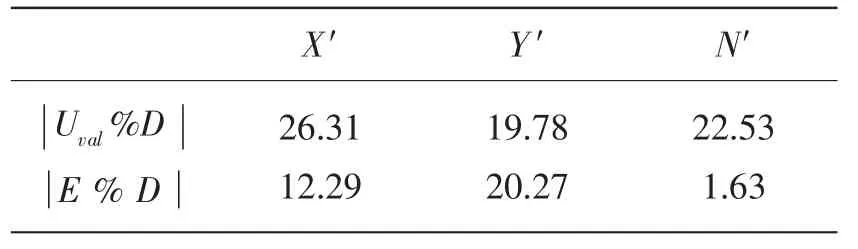
表3 X′，Y′，N′的确认分析结果Tab.3 Validation results of X′,Y′,N′

4.2 确认：模型误差的评估

以上讨论的是在网格离散过程中的数值误差和不确定度，为了更深入地探讨误差问题，还需对数值建模过程中的模型精度作进一步分析，即评估模型误差和不确定度。本文采用美国机械工程师协会（American Society of Mechanical Engineers，ASME）发表的V&V 20-2009标准[3]中的方法，结合INSEAN的试验数据（包括试验不确定度），针对同一工况h/T=1.2，β=4°进行确认分析。在ASME标准的确认分析方法中，引入了确认不确定度和比较误差两个参数。S为数值解，USN为其对应的数值不确定度；D为试验数据，UD为对应的试验测量不确定度。若，说明模型误差隐含在由数值不确定度和试验不确定度带来的“噪声（noise）”里，因而无法对模型误差做出评估；而若，则表示建模过程存在模型误差，需要结合比较误差E的大小和符号来改进模型。表3列出了本文研究中水动力系数X′，Y′，N′的确认不确定度和比较误差。X′，Y′，N′三者的平均误差在11%左右，与SIMMAN2008专题讨论会[6]上其他机构研究结果的精度水平一致。比较两个参数可以看到，X′和N′的确认不确定度都远大于比较误差，意味着模型误差并不明显；Y′的十分接近，比较误差稍大，所以还需要进一步的考察来确定模型可能存在的问题。

4.3 模型误差的来源分析

对浅水斜航KVLCC2船模的水动力预报中，可能存在的模型误差源有以下几个方面：

a.计算区域纵向尺度的影响；

b.湍流模型的影响；

c.水底和岸壁的简化边界条件的影响；

d.忽略船体自由下沉和纵倾的影响。

为检查每一误差源，本文逐一进行模型改进和新的数值计算。首先为考察计算区域纵向尺度的影响，将x方向尺度增大，把入口和出口边界面都设置在船前和船后2LPP处。而y和z方向由于要保证和模型试验的浅水、岸壁条件一致，所以保持不变。然后，用Menter的k-ω SST模型代替之前采用的EASM模型来判别湍流模型的影响。此外，原计算中水底和岸壁的边界条件采用滑移条件简化计算，而实际上斜航船体对水底/岸壁存在相对运动，在水底面（受船体扰动影响更大）上会形成边界层，因此在底/岸上采用移动壁面（无滑移）条件。最后，低速下的自由面兴波往往很小，对水动力的影响不大，所以将船体浮态的改变和自由面效应一并忽略。但是在浅水条件下，由于其阻塞作用，对船体浮态（下沉和纵倾）可能有一定影响，而下沉和纵倾的改变也会引起水动力的变化。再者，模型试验中船体是可以自由下沉和纵倾的。为此，将初始计算得到的下沉和纵倾看作流场中船舶调整后的姿态，将其加入新的计算当中来模拟船体自由下沉和纵倾对水动力的影响。

表4 各误差源对应的Uval和Tab.4 Uvalandof different sources of modelling error

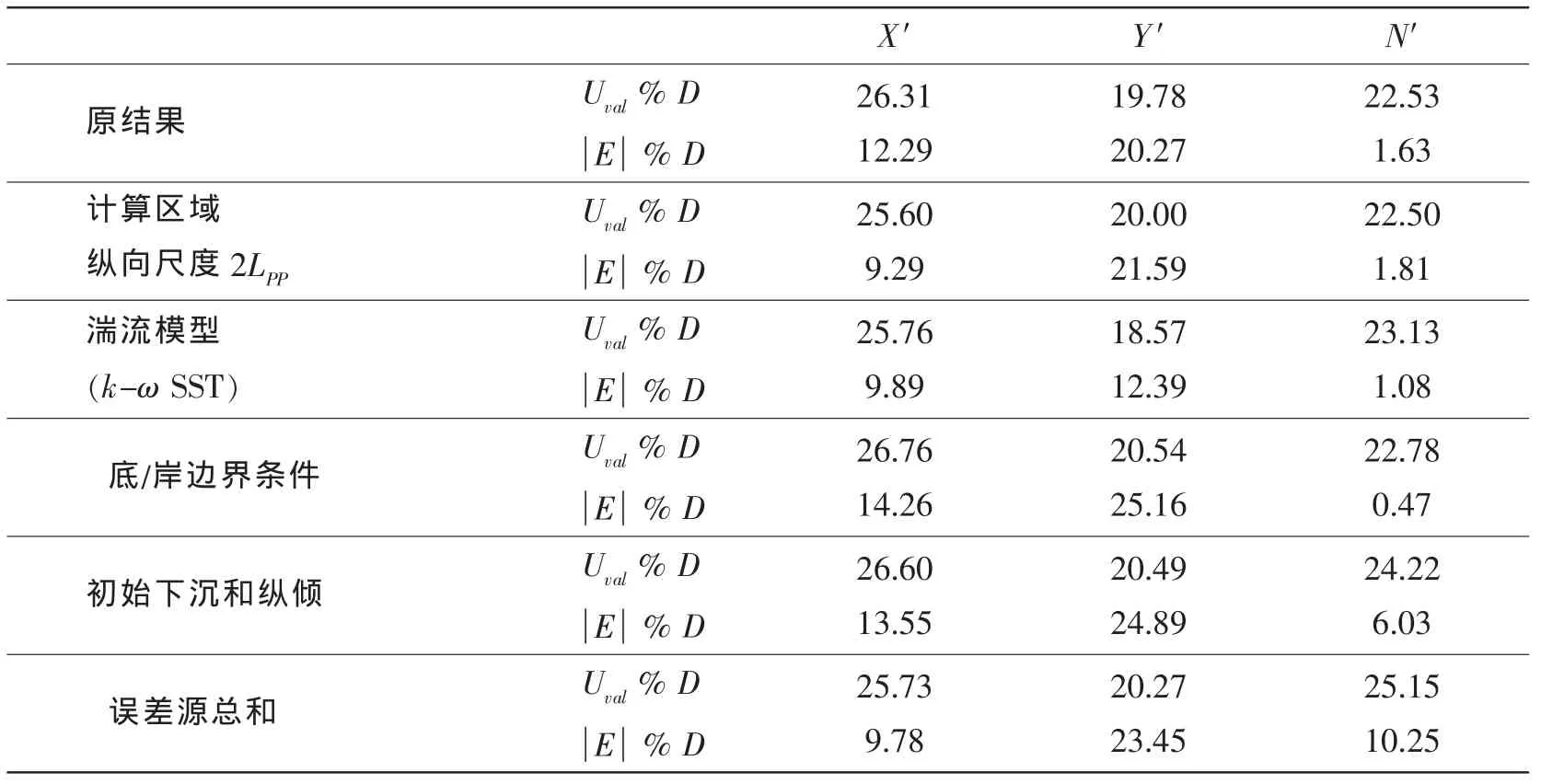
表4 各误差源对应的Uval和Tab.4 Uvalandof different sources of modelling error

X′ Y′ N′22.53 1.63计算区域纵向尺度2LPP?原结果Uval%D E%D 26.31 12.29 19.78 20.27 22.50 1.81湍流模型（k-ω SST）Uval%D E%D 25.60 9.29 20.00 21.59 Uval%D E%D 25.76 9.89 18.57 12.39 23.13 1.08底/岸边界条件初始下沉和纵倾误差源总和Uval%D E%D Uval%D E%D Uval%D E%D 26.76 14.26 26.60 13.55 25.73 9.78 20.54 25.16 20.49 24.89 20.27 23.45 22.78 0.47 24.22 6.03 25.15 10.25

对以上四个误差源分别进行调整和重新计算后，得到确认所需参数，如表4所列。与原结果对比可见，将计算区域的纵向尺度加大后，纵向力系数X′的比较误差降低了3%左右，而横向力和转首力矩的误差变化不大；三个水动力系数的对比结果并无改变。湍流模型k-ω SST对X′和N′结果的影响与计算区域尺度类似，但是将Y′的误差降低了近8%并使其比较误差小于确认不确定度，在某种程度上降低了模型误差的影响。此外，底/岸的移动岸壁边界条件增大了X′和Y′的误差，却稍微降低了N′的误差，原因还有待查证。而加入初始下沉和纵倾量后，也使得三个水动力系数的比较误差较原计算有所增大。最后，在计算中综合四个误差源改进后，可以看到本质上并没有改变原确认结果，但是Y′和N′的确认不确定度和比较误差都有所增加，尤其是N′。

4.4 漂角对水动力系数的影响

在以上分析的基础上，对其他漂角情况进行类似的计算（分别采用原计算设置和综合改进四个误差源的设置），得到相关水动力系数，如图6所示。

计算得到的X′，Y′，N′均随β的增加而变大，与INSEAN的试验数据相比可以看到Y′，N′的变化趋势与试验一致，但是X′结果和试验数据的趋势不同。在前期深水情况的数值计算中[11]，X′的计算结果与INSEAN试验值的对比也存在类似问题，但计算结果与其他比较试验结果一致。另外，本文X′计算结果与Toxopeus等人[8]的也相符，所以考虑X′变化趋势的误差与试验中测量的误差和不确定度有关。Y′，N′变化趋势的数值预报结果虽然较好，但是数值上的精度仍然不够高。另一方面，图6显示综合改进前文所述的四个误差源后，得到的结果与原计算结果的趋势一致。数值上X′和N′较原结果都有所增大；Y′值在β=0～4°上的改变并不明显，但在β=6°处比原值要大。

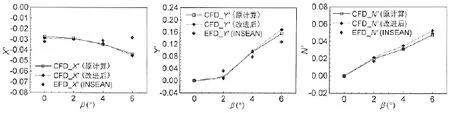
图6 X′，Y′，N′随漂角的变化Fig.6 X′,Y′,N′against drift angle

5 结 语

本文采用基于定常RANS方程的数值计算方法预报了在浅水中低速斜航运动船舶的水动力系数。为了把握数值计算中的误差和不确定度以便为提高计算精度提供必要的参考信息，文中采用系统的验证和确认方法，评估和分析计算中的数值误差以及模型误差。研究结果显示本文预报的浅水中水动力系数变化趋势与试验数据一致，但计算的精度问题仍然存在，平均误差在11%左右。在确认分析中，纵向力和转首力矩与试验的比较误差比数值和试验的不确定度之和要小，所以不易判别模型误差；而横向力系数的比较误差与确认不确定度非常接近甚至前者稍大，所以存在某种模型误差。文中考虑了四种可能的误差源：计算区域纵向尺度、湍流模型、底/岸边界条件、初始下沉和纵倾，分析结果表明这四个误差源对水动力系数的影响各不相同，唯一将横向力误差降低的是湍流模型k-ω SST；而综合所有的误差源并没有直接提高横向力和转首力矩的精度，可见确定模型误差源的复杂性，在今后的研究中还需更多的探讨。

[1]Roache P J.Verification and validation in computational science and engineering[M].Hermosa Publishers,Albuquerque, 1998.

[2]ITTC,7.5-03-01-01.CFD general:Uncertainty analysis in CFD-verification and validation methodology and procedures [K].Quality Manual,2002.

[3]ASME V&V 20-2009.Standard for verification and validation in computational fluid dynamics and heat transfer[S].American Society of Mechanical Engineers,New York,UK,2009.

[4]Eça L,Vaz G,Hoekstra M.A verification and validation exercise for the flow over a backward facing step[C]//Proceedings of the V European Conference on Computational Fluid Dynamics,ECCOMAS CFD 2010.Eds.Pereira J C F,Sequeira A,Lisbon,Portugal,2010.

[5]Zou L,Larsson L.A V&V study based on resistance submissions to the Gothenburg 2010 workshop on numerical ship hydrodynamics(Chapter 5,Book name:Numerical Ship Hydrodynamics-An Assessment of the Gothenburg 2010 Workshop. Editors:Larsson L,Stern F,and Visonneau M)[C].Springer,ISBN:978-94-007-7188-8,2013.

[6]SIMMAN 2008 Workshop[C].Available at:http://www.simman 2008.dk,Copenhagen,Denmark,2008.

[7]Simonsen C D,Stern F,Agdrup K.CFD with PMM test validation for manoeuvring VLCC 2 tanker in deep and shallow water[C]//Proceedings of the International Conference on Marine Simulation and Ship Manoeuvrability,MARSIM 2006. Terschelling,Netherlands,M-4-1,2006a.

[8]Toxopeus S L,Simonsen C D,Guilmineau E,Visonneau E G,Xing T,Stern F.Investigation of water depth and basin wall effects on KVLCC2 in manoeuvring motion using viscous-flow calculations[J].Journal of Marine Science and Technology, 2013,DOI 10.1007/s00773-013-0221-6.

[9]田喜民,邹早建,王化明.KVLCC2船模斜航运动粘性流场及水动力数值计算[J].船舶力学,2010,14(8):834-840. Tian Ximin,Zou Zaojian,Wang Huaming.Computation of the viscous flow and hydrodynamic forces on a KVLCC2 model in oblique motion[J].Journal of Ship Mechanics,2010,14(8):834-840.

[10]钱永峰.浅水中作斜航运动船体粘性绕流计算[D].华中科技大学,2007.

[11]Zou L,Larsson L,Orych M.Verification and validation of CFD predictions for a manoeuvring tanker[J].Journal of Hydrodynamics,Ser.B,2010,22(5):438-445.

[12]Roe P L.Approximate riemann solvers,parameter vectors,and difference schemes[J].Journal of Computational Physics, 1981,43:357-372.

[13]Chakravarthy S,Osher S.A new class of high accuracy TVD schemes for hyperbolic conservation laws[J].AIAA Paper, No.85-0363,1985.

[14]Chorin A.A numerical method for solving incompressible viscous flow problems[J].Journal of Computational Physics, 1967,2:12-26.

[15]Menter F R.Zonal two equation k-ω turbulence models for aerodynamic flows[C]//Proceedings of the 24th Fluid Dynamics Conference.Orlando,AIAA paper 93-2906,1993.

[16]Gatski T B,Speziale C G.On explicit algebraic stress models for complex turbulent flows[J].Journal of Fluid Mechanics, 1993,254:59-78.

Numerical predictions of hydrodynamic forces on a ship during a low-speed drift motion in shallow water including verification and validation

ZOU Lu
(School of Naval Architecture,Ocean and Civil Engineering,Shanghai Jiao Tong University,Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration,Shanghai 200240,China)

Travelling at a drift angle in shallow water,the ship is affected by both the asymmetry flow and the blockage from shallow water.To predict the hydrodynamic forces on the ship,this paper applies a Computational Fluid Dynamics method based on the steady state Reynolds-Averaged Navier-Stokes equations to solve the viscous flow around the ship during a low-speed drift motion in shallow water.Considering the ship moves at a low speed,the effects of free surface are assumed negligible.Tendencies of the hydrodynamic forces against the drift angle are simulated from numerical computations.For the purpose of evaluating the degree of accuracy in the numerical results,verification and validation analyses are performed.The numerical error and uncertainty are estimated from a grid convergence study,while the modelling errors are investigated along with the experimental data.In addition,the contributions of computational domain size, turbulence model,boundary condition,as well as the influence of sinkage and trim to the modelling errors are discussed.This study offers a useful reference for the improvement of the numerical model and the ac-curacy in numerical predictions.

shallow water;drift motion;CFD;hydrodynamic forces;error and uncertainty; verification and validation

U661.1

：Adoi:10.3969/j.issn.1007-7294.2016.07.007

1007-7294（2016）07-0841-08

2016-01-20

国家自然科学基金项目（51309152）；高性能船舶技术教育部重点实验室开放基金课题资助项目（2013033101）

邹 璐（1983-），女，博士，助理研究员，E-mail：luzou@sjtu.edu.cn。