基于变点分析思想的高维机械噪声数据本征维估计方法

梁胜杰，张志华，高绍忠，胡俊波，李大伟

（1.91697部队，山东 青岛 266405；2.海军工程大学 科研部，武汉 430033；3.91550部队，辽宁 大连116023）

基于变点分析思想的高维机械噪声数据本征维估计方法

梁胜杰1，张志华2，高绍忠1，胡俊波2，李大伟3

（1.91697部队，山东 青岛 266405；2.海军工程大学 科研部，武汉 430033；3.91550部队，辽宁 大连116023）

利用变点分析思想，针对高维数据协方差矩阵的特征值曲线特点，提出一种本征维估计方法：基于均值估计的特征值变点法，并应用于某双层圆柱壳体的机械噪声数据处理中。通过与其他现有常用方法的比较分析，验证了基于均值估计特征值变点法的可行性。结果显示：基于均值估计的特征值变点法理论简单、计算简便，计算结果客观、合理，对某双层圆柱壳体机械噪声数据的处理效果较好。

高维数据；本征维；变点分析；判别分析；机械噪声数据

0 引 言

智能计算技术的发展使得工程上待处理的数据对象变得越来越复杂，数据维数越来越高，如遥感图像数据、机械振动信号、雷达目标信号、地震资料数据等等。高维数据的特征空间中通常含有许多冗余特征，这些特征增加了学习、训练的时间及空间复杂度，降低了分析处理的精度。因此，在对高维数据进行分析前，应进行降维预处理[1]。

降维是指从原始数据较多的特征量中利用数学统计方法提取出具有代表意义的典型特征变量，以达到简化数据的目的。常用方法如主成分分析法、因子分析法等。为叙述方便，我们将提取出来的典型特征量称为本征特征量（如主成分分析法中的主元、因子分析法中的因子等），典型特征量的个数称为本征维。降维过程中，一个重要步骤就是确定本征维，如主成分分析方法中的主元数目[2]。错误的本征维（低估或高估）将导致数据分析结果的错误，如低估本征维将导致有用信息的损失及造成对计算结果本质的曲解；高估本征维将保留具有较少重要载荷的特征量，这些特征量很难被解释其意义[3]。

目前本征维估计方法主要分为两类：基于特征值的估计方法和基于分形思想的估计方法。基于分形思想的估计方法可以较准确地估计出数据的本征维[4]，但为了获得D维数据准确的本征维，要求观测样本量满足的条件，样本量过大，大大增加了试验难度；基于特征值的估计方法原理简单、计算方便，在工程上得到广泛应用，常用方法如以“特征值大于1”为标准的方法（Eigenvalue-greaterthan-one rule，K1法）[5]、平行分析法（Parallel Analysis，PA法）[6]，碎石图检验法（Scree Test，SCREE法）[7]，最小平均偏相关法（Minimum Average Partial，MAP法）[8-9]和累计贡献率法（Proportion of total variation，PTV法）[10]等。因此，本文将基于特征值研究高维数据的本征维估计方法。

基于特征值的估计方法均依据原始数据协方差矩阵的特征值进行计算，其原理不同，估计结果也不尽相同，各有特点：K1法过于主观，人们无法解释为什么认为特征值1.01对应的主元是重要的，而认为特征值0.99对应的主元不重要[11]；PA法是一种蒙特卡洛模拟法，计算中将花费大量时间，不适宜处理大样本和高维数据集；SCREE法比K1法更加主观和模棱两可，尤其是在“肘点”不明显或多于两个“肘点”情况下[12]；MAP法相比上述几种方法来说能够得到较精确的结果，但要求主元中含有较多的原始变量[3]，不适宜处理维数较低的数据集；PTV法在确定累计贡献率标准时同样具有较强的主观性，如可选50%[13]、80%[14]或95%[15]等。由于上述方法的种种缺点，导致目前比较普遍使用的统计程序也未能为使用者提供最精确的本征维估计方法[16]。

鉴于上述问题，本文将针对特征值曲线简单、直观的优点，利用统计学中成熟的变点分析思想，提出一种明确、客观的高维数据本征维估计方法：基于均值估计的特征值变点法（Eigenvalue Chang-point Method based mean estimating，meanECP），并应用于某双层圆柱壳体机械噪声数据的预处理之中。与现有方法相比，本文方法效果较好。

1 特征值变点法

变点分析研究始于20世纪50年代。自诞生以来，变点问题一直是统计中的一个热门话题。变点技术早期主要应用于工业自动控制领域，随着计算机技术的发展，现在已在医学、金融、水文研究、交通流研究等[17-21]领域得到广泛应用。

1.1 特征值变点定义

变点是指“模型中的某个或某些量起突然变化之点”[22]。这种突然变化往往反映事物的某种质的变化。对工程中的高维数据来说，在利用降维方法降维过程中，首先需要计算其协方差矩阵的特征值，并将这些特征值按从大至小的次序排列。则在高维数据协方差矩阵的特征值曲线中某个特征值起突然变化之点就是变点，就称为特征值变点。

利用特征值变点可以将高维数据协方差矩阵特征值对应的特征量按典型和非典型分开，得到的典型特征量即认为是原始数据经降维后的本征维，典型特征量的个数即原始数据的本征维。特征值变点分析的主要任务是对这种突变点给予客观的划分标准。事实上，SCREE法利用观测所确定的“肘点”也是特征值曲线的一个变点，而此变点是通过观察碎石图得到，受主观影响较大。本文将利用变点分析的统计知识给出特征值曲线变点的客观数值解。

1.2 数学模型

变点分析包括两类模型：离散型和连续型。已知高维数据协方差矩阵的特征值是按从大到小排列的离散值，本文将建立离散型特征值变点分析模型。设λ1，λ2，…，λn为来自母体的特征值抽样，且

λ1，λ2，…，λn之间相互独立，若

现在成熟的变点分析方法有：最小二乘法、极大似然法、Bayes法和局部比较法等[23]。本文将在上述方法的基础上，利用变点分析思想提出一种用于估计高维数据本征维的特征值变点法。

1.3 均值估计法

对于相互独立的λ1，λ2，…，λn特征值抽样，设

其中：a1≠a2，随机误差ξ1，ξ2，…，ξn相互独立，期望为0，方差为σ2，则称k为特征值变点。

在特征值曲线上取第i个特征值点，位置坐标为（i，λi），记为b点。其前后两个特征值点c点：（i+ 1，λi+1）和a点记线段与夹角为B。

由 λi-1≥λi≥λi+1可知如图1中（Ⅰ）、（Ⅱ）两种情况所示。

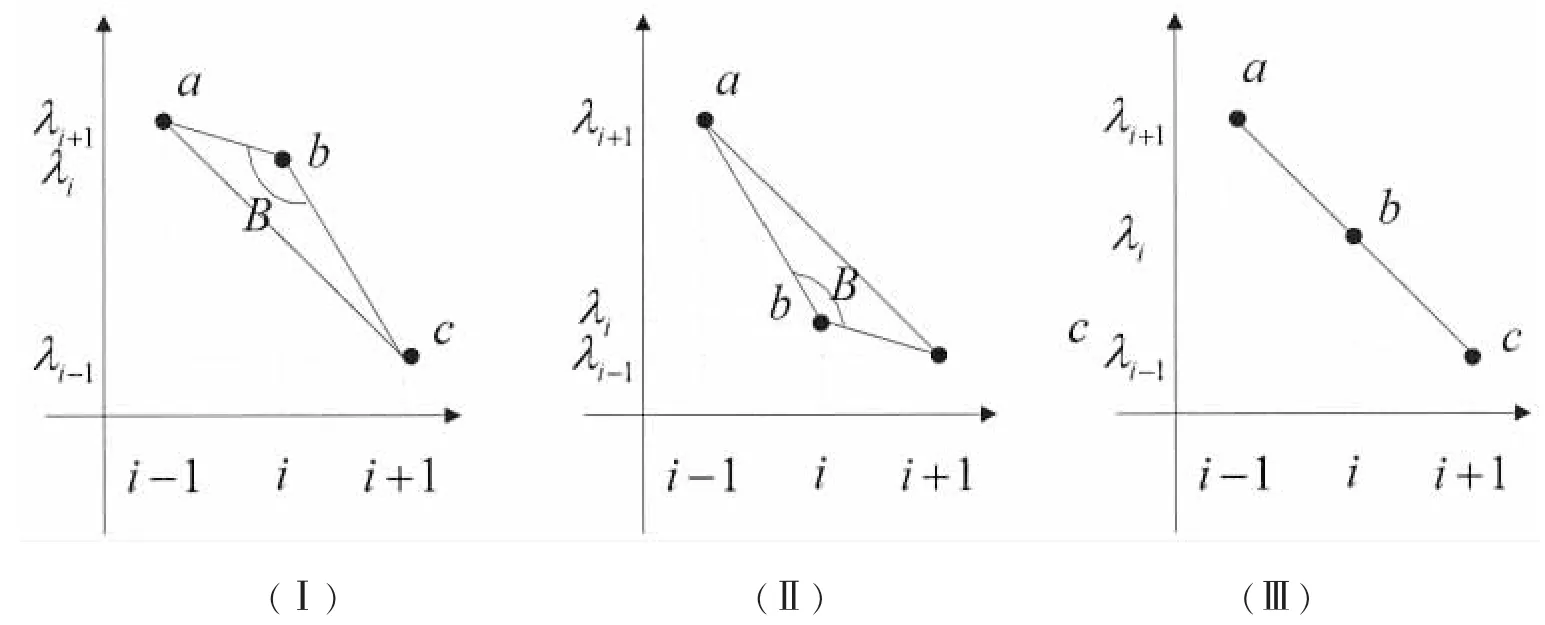
图1 相邻三个特征值点夹角示意图Fig.1 Sketch map of included angle between the three contiguous eigenvalue points

当B=π时，点a、b、c在同一直线上，此时无变点，三点对应的特征值均值相同。如图1（Ⅲ）所示；随着夹角B逐渐趋向于当λi-1=λi≠λi+1或λi-1≠λi=λi+1时，B达到最小值，此时变点最明显，变点位置为i。由上述分析可知：当无变点时，有即点a、c的纵坐标均值估计与点b的横坐标相等；当有变点时即点a、c的纵坐标均值估计与点b的横坐标存在一定误差，且当时误差最大，此时变点最明显。因此，本文将利用均值估计误差Δλi（1≤i≤n）对变点位置进行估计：

除变点估计技术外，变点分析方法还应包括变点检验技术[22]。由于本文处理的对象是特征值曲线，且主要是通过估计一个较小的本征维达到降低观测数据维数的目的，故认为该特征值曲线存在变点，而不需要做变点检验。

1.4 估计步骤

设高维数据Y是一n×N型矩阵，即

其中：n为维数，N为样本个数。为简化叙述，通常假定Y是经过中心化后样本矩阵。则meanECP法估计高维数据本征维的步骤如下：

（1）标准化高维数据矩阵：

其中：Q是Y的协方差矩阵平方根的逆矩阵；

（3）计算

其中：i=2，…，n-1；

2 方法应用及比较分析

将meanECP法用于某双层圆柱壳体机械噪声数据的本征维估计中，并与其它常用方法进行比较。

2.1 数据来源

某双层圆柱壳体的机械振动噪声数据主要来自三个设备：海水泵、电机和激振器。在壳体的不同位置布置19个加速度传感器（每个传感器称为一通道），设定八个不同工况，如表1所示[24]。

设定采样时间8 s，采样频率2 048 Hz，则每一工况在每一通道上都可测得16 384个样本数据。

由于同一个通道下的采样点较多，且特征单一，不易分析数据的规律特点，因此需要对样本点进行预处理：

（1）选定信号处理中常用的10个特征量[24]：波形因数，峰值因数，脉冲因数，振动加速度总级，期望，方差，标准差，三阶累量，四阶累量，有效值；

（2）以2 048个相邻样本点为一个样本段，并以70个样本点为步长，将样本段逐步向后平移，可在16 384个样本点内得到约205个样本段；

（3）每一工况下随机选择100个样本段，在每个样本段内计算选定的十个特征量。

本文是为了验证基于变点分析思想估计本征维的可行性，及比较与现有方法的效果好坏，故只选取10个常用的特征量和随机抽取了100个样本段作为举例，实际上可以选择更多的特征量和样本段。

预处理后，在每一工况下的每一通道上可得到一个10*100噪声数据。其中，10是维数，100是样本量。则在八种工况下，每一条通道上可得到一个10*800数据。

2.2 计算结果

对2.1节的试验数据，分别使用K1法、PA法、SCREE法、MAP法、PTV法及meanECP法进行处理，得到噪声数据在19条通道上的本征维，及不同方法的程序运行时间（程序运行平台为Matlab R2009a），结果如表2和表3所示。

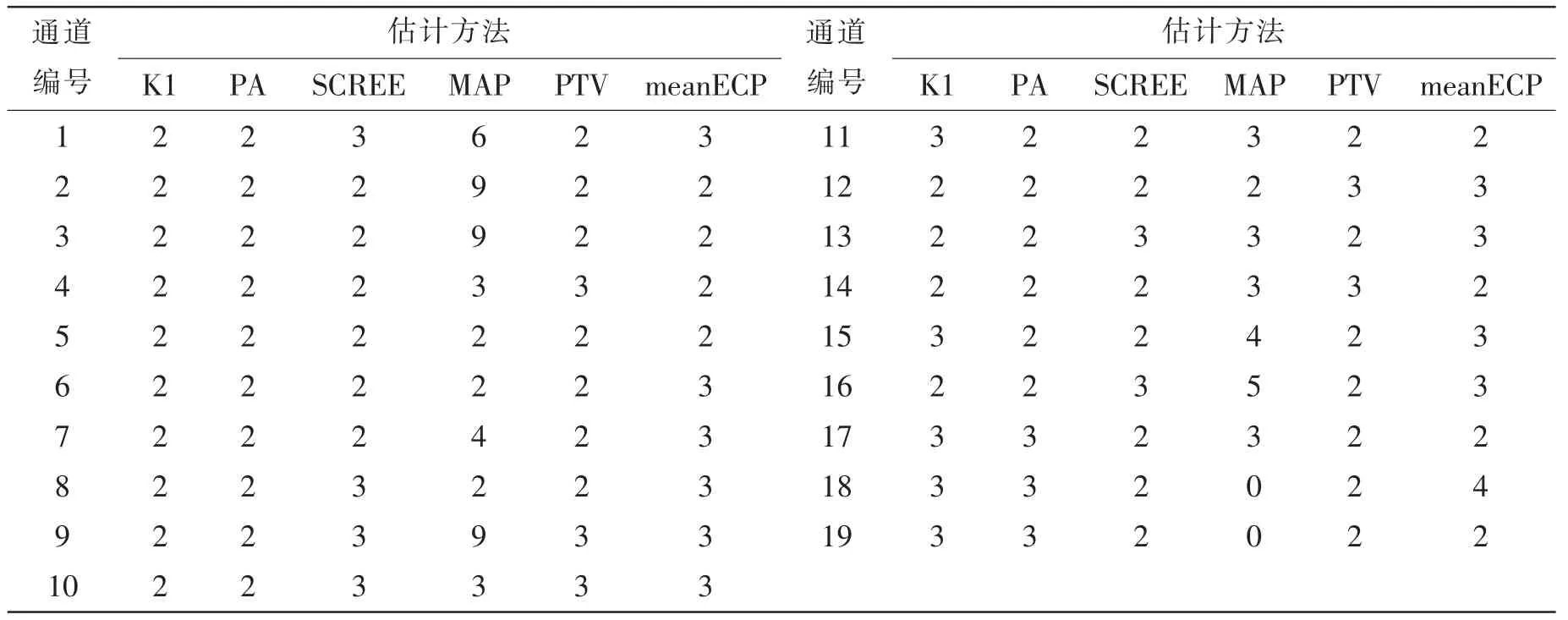
表2 本征维估计结果Tab.2 Latent characteristic variables dimensionality

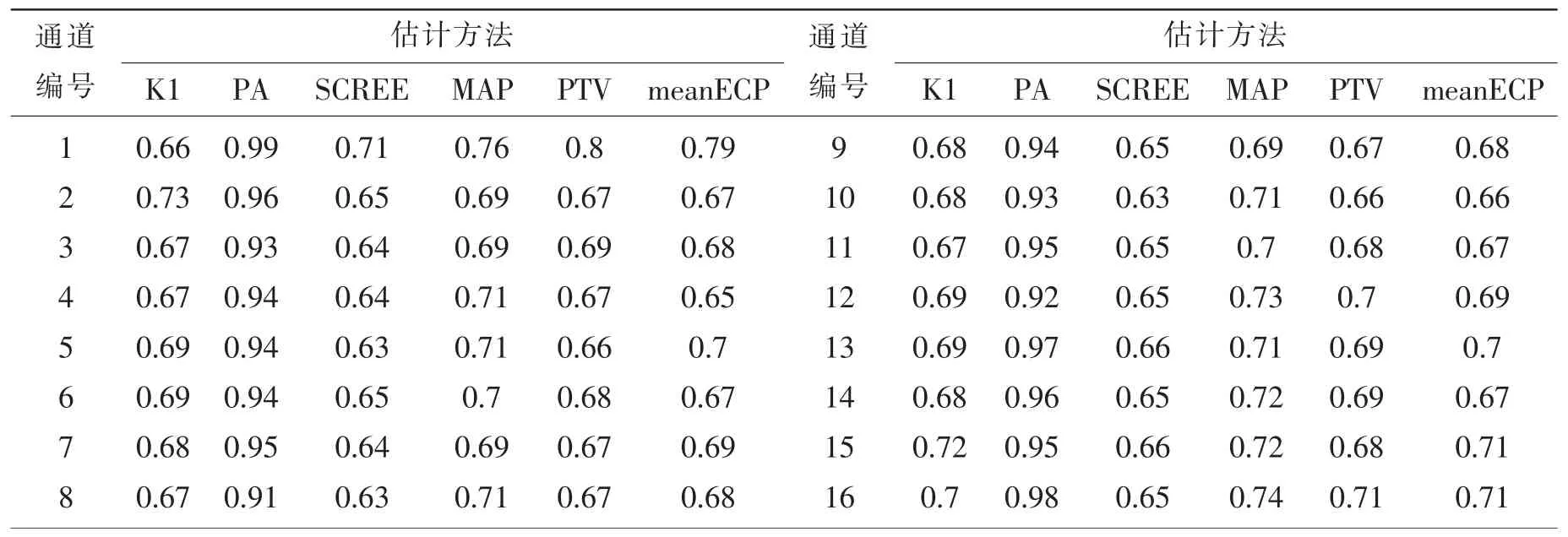
表3 不同估计方法运算时间（单位：秒）Tab.3 Computing time of different methods(Unit:s)

续表3

表3中最后一行“时间”表示不同方法在19条通道上程序执行时间的平均值。为直观比较不同方法效果，图2～7以第7通道为例，显示了6种方法的本征维估计结果。其中PA法以蒙特卡洛模拟的特征值均值线和0.95百分位线为标准[25]，两个标准估计的结果相同；MAP法中原始MAP指的是Velicer于1976年提出的以偏相关系数平方的最小平均值为标准，改进MAP是指Velicer于2000年提出的以偏相关系数四次方的最小平均值为标准；PTV法中以0.95为标准[15]。

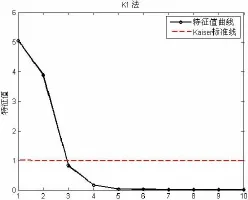
图2 第七通道上K1法估计结果图Fig.2 Evaluating result of K1 method in seventh sensor

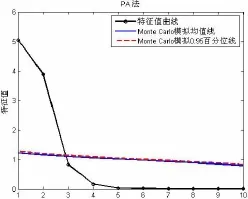
图3 第七通道上PA法估计结果图Fig.3 Evaluating result of PA method in seventh sensor

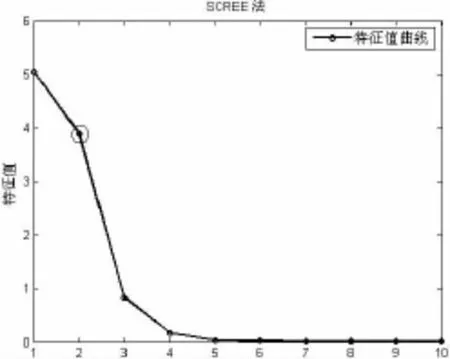
图4 第七通道上SCREE法估计结果图Fig.4 Evaluating result of SCREE method in seventh sensor

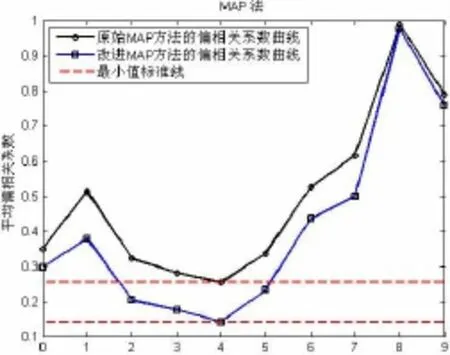
图5 第七通道上MAP法估计结果图Fig.5 Evaluating result of MAP method in seventh sensor

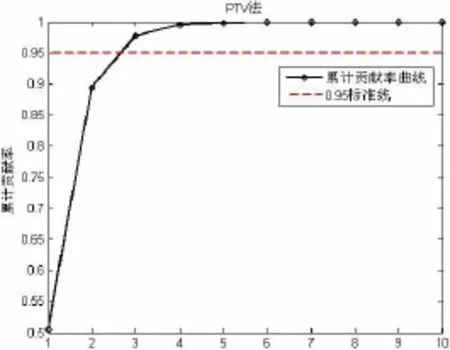
图6 第七通道上PTV法估计结果图Fig.6 Evaluating result of PTV method in seventh sensor

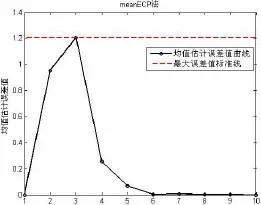
图7 第七通道上meanECP法估计结果图Fig.7 Evaluating result of meanECP method in seventh sensor

2.3 比较分析

表2中结果显示，MAP方法估计的本征维较其他方法大，且在不同通道上的变化波动也较大；同时，第18、19通道上估计的本征维为0，说明MAP方法对这两通道不适用；由K1法、PA法、SCREE法、PTV法的计算结果可知，在所有19条通道上的某双层圆柱壳体机械噪声数据的本征维在2与3范围内，由meanECP法估计的本征维同样也在2、3两位置浮动（只在第18通道上估计结果为4），从而验证了meanECP的可行性。

由表3可知，PA方法的程序运算时间明显高于其他方法，说明该法不适宜处理大样本或高维数的观测数据。同时，由于SCREE法与PTV法受主观影响较大。因此，对于某双层圆柱壳体机械噪声数据来说K1法与meanECP法较合适。

为进一步比较K1法与ECP法的效果，下面将利用判别分析方法确定噪声数据在两种方法估计的本征维下对每一条通道上来自不同工况样本的判别分析结果。基本思想是：限定某一通道，对该通道上来自八个不同工况的100个观测样本组成的10*800数据矩阵进行主成分分析，并分别利用K1法和meanECP法估计本征维，然后根据估计的本征维对来自不同工况的样本利用判别分析进行分类，依据分类正确率的大小比较估计效果：分类正确率越高，说明估计的本征维越合理，估计方法效果越好。19条通道上的判别分析结果如表4所示（程序运行平台：SPSS 17.0）。

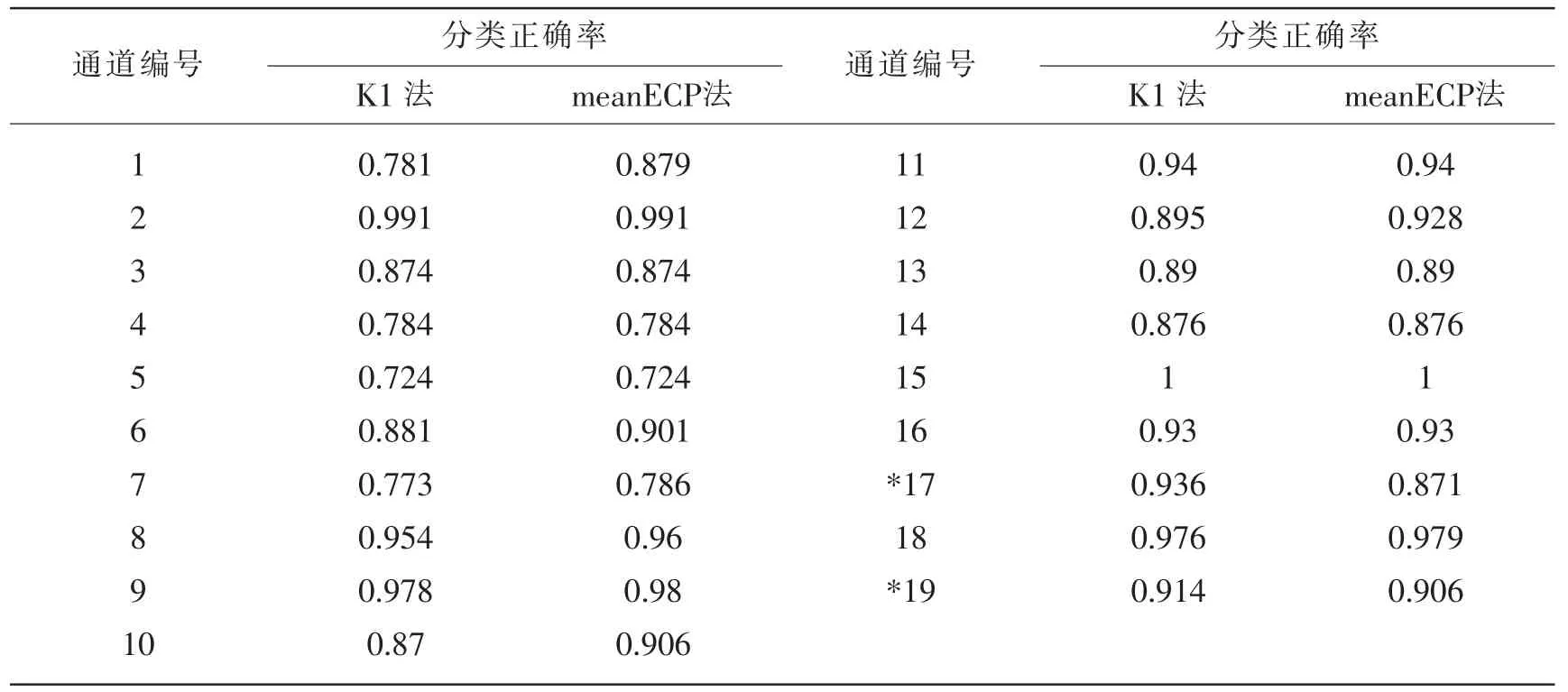
表4 K1法与meanECP法的判别分析结果比较Tab.4 Results of discrimnant analysis between the K1 method and the meanECP method

表4中，除第17、18通道外，其余通道上均显示meanECP法的估计效果比K1法的估计效果好。

3 结 论

基于均值估计的特征值变点法是在现有常用本征维估计方法基础上，充分利用变点分析思想提出来的。通过对现有变点位置估计技术的改进，基于均值估计提出了一种针对特征值曲线特点的变点估计方法。通过在某双层圆柱壳体机械噪声数据中的实际应用，验证了基于均值估计的特征值变点法（meanECP法）在高维数据本征维估计中的可行性。最后通过分析，与现有常用的本征维估计方法进行了比较。结果显示：meanECP法理论简单、计算简便，计算结果客观、合理，对某双层圆柱壳体机械噪声数据具有较好的处理效果。

参 考 文 献：

[1]van der Maaten L J P,Postma E O,van den Herik H J.Dimensionality reduction:a comparative review[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2009(10):1-35.

[2]Rubén D L,Pedro V.Determining the number of factors to retain in EFA:An easy-to-use computer program for carrying out Parallel Analysis[J].Practical Assessment,Research&Evaluation,2007,12(2):1-11.

[3]Zwick W R,Velicer W F.Comparison of five rules for determining the number of components to retain[J].Psychological Bulletin,1986,99(3):432-442.

[4]Camastra F,Vinciarelli A.Estimating the intrinsic dimension of data with a fractal-based method[J].IEEE Trans.Pattern Anal Mach Intell,2002,24(10):1404-1407.

[5]Kaiser H F.The application of electronic computers to factor analysis[J].Educational and Psychological Measurement, 1960,20:141-151.

[6]Horn J L.A rationale and test for the number of factors in factor analysis[J].Psychometrika,1965,30(2):179-185.

[7]Cattell R B.The scree test for the number of factors[J].Multivariate Behavioral Research,1966(1):245-276.

[8]Velicer W F.Determining the number of components from the matrix of partial correlations[J].Psychometrika,1976,41 (3):321-327.

[9]Velicer W F,Eaton C A,Fava J L.Construct explication through factor or component analysis:A review and evaluation of alternative procedures for determining the number of factors or components[M].Problems and solutions in human assessment:Honoring Douglas N.Jackson at seventy,Boston:Kluwer Academic Publishers,2000:41-71.

[10]Jolliffe I T.Principal component analysis(second edition)[M].New York:Springer-Verlag,2002.

[11]Fabrigar L R,Wegener D T,Maccallum R C,et al.Evaluating the use of exploratory factor analysis in psychological research[J].Psychological Methods,1999(3):272-299.

[12]Hayton J C,Allen D G,Scarpello V.Factor retention decisions in exploratory factor analysis:a tutorial on parallel analysis[J].Organizational Research Methods,2004,7:191-205.

[13]Streiner D L.Figuring out factors:The use and misuse of factor analysis[J].Canadian Journal of Psychiatry,1994,39: 135-140.

[14]Floyd F J,Widaman K F.Factor analysis in the development and refinement of clinical assessment instruments[J].Psychological Assessment,1995,7:286-299.

[15]Jackson D A.Stopping rules in principal components analysis:a comparison of heuristical and statistical approaches[J]. Ecology,1993,74(8):2204-2214.

[16]Costello A B,Osborne J W.Best practices in exploratory factor analysis:four recommendations for getting the most from your analysis[J].Practical Assessment Research&Evaluation,2005,10(7):1-9.

[17]Andreou E,Ghysels E.Structural breaks in financial time series[M].Handbook of Financial Time Series,Berlin Heidelberg:Springer-Verlag,2009:6,839-870.

[18]关文韬,金百锁,缪柏其.原油价格与黄金价格的变点分析[J].中国科学技术大学学报,2014,44(6):502-507. Guan Wentao,Jin Baisuo,Miao Baiqi.Change-point analysis of crude oil and gold prices[J].Journal of University of Science and Technology of China,2014,44(6):502-507.

[19]熊立华,于坤霞,董磊华等.水文时间序列变点分析的可靠性检验[J].武汉大学学报(工学版),2011,44(2):137-141. Xiong Lihua,Yu Kunxia,Dong Leihua,et al.Reliability test for detecting change point of hydrological time series[J]. Engineering Journal of Wuhan University,2011,44(2):137-141.

[20]危润初,肖长来,方 樟.黑龙江建三江地区地下水动态趋势突变点分析[J].吉林大学学报:地球科学版,2016,46 (1):202-210. Wei Runchu,Xiao Changlai,Fang Zhang.Trends mutation nodes of groundwater dynamic in jiangsanjiang area of heilongjiang province[J].Journal of Jilin University(Earth Science Edition),2016,46(1):202-210.

[21]Céline L,François R.Detection and localization of change-points in high-dimensional network traffic data[J].The Annals of Applied Statistics,2009,3(2):637-662.

[22]陈希孺.变点统计分析简介(I)[J].数理统计与管理,1991,10(1):55-58. Chen Xiru.The overview of statistical analysis and case study of change points(I)[J].Journal of Applied Statistics and Management,1991,10(1):55-58.

[23]Csorgo M,Horvath L.Limit theorems in change-point analysis[M].London:John Wiley&Sons,1997.

[24]张志华,梁胜杰,尹曰建等.基于SVM的双层圆柱壳体机械振动噪声数据特征提取方法比较[J].船舶力学,2015,19 (1-2):215-220. Zhang Zhihua,Liang Shengjie,Yin Yuejian,et al.Comparison of feature extraction methods on mechanical vibrating noise of ribbed cylindrical double-shells based SVM[J].Journal of Ship Mechanics,2015,19(1-2):215-220.

[25]Raiche G,Riopel M,Blais J G.Non Graphical Solutions for the Cattel’s Scree Test[C]//International Meeting of the Psychometric Society(IMPS 2006).HEC,Montreal,2006.

A method of latent characteristic variables dimensionality evaluating of High-dimensional mechanical noise data based Change-Point analysis

LIANG Sheng-jie1,ZHANG Zhi-hua2,GAO Shao-zhong1,HU Jun-bo2,LI Da-wei3
(1.91697 PLA troops,Qingdao 266405,China;2.Dept.of Scientific Research,Naval University of Engineering, Wuhan 430033,China;3.91550 PLA troops,Dalian 116023,China)

According to eigenvalue-curve’s characteristic of covariance matrix from a High-dimensional data,a new method of latent characteristic variables dimensionality evaluating is proposed based change-point analysis technology,which called Eigenvalue Change-point method based mean estimating,and then apply it to deal with the mechanical noise data of ribbed cylindrical double-shells.Through the analysis comparing with other methods,the proposed method was validated in its feasibility.It is also verified that Eigenvalue Change-point method based mean estimating is simply in theory and convenient in computing;its compute result is impersonal and reasonable;meanwhile,it has attained a preferable result when dealing with the mechanical noise data of a ribbed cylindrical double-shells.

High-dimensional data;latent characteristic variables dimensionality;Change-Point Analysis; Discriminant Analysis;mechanical noise data

TB53 O212.4

A

10.3969/j.issn.1007-7294.2016.07.015

1007-7294（2016）11-1485-09

2016-07-20

国家自然科学基金（50775218）

梁胜杰（1981-），男，博士，E-mail：lsj990308@163.com；张志华（1965-），男，教授，博士生导师；高绍忠（1963-），男，高级工程师；胡俊波（1982-），男，博士；李大伟（1985-），男，博士。