一种新的海洋平台管节点应力评估方法

粟 京，赵晓玲，刘 刚

（1.中国海洋石油总公司，北京 100028；2.大连船舶重工集团设计研究所，辽宁 大连 116005；3.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

一种新的海洋平台管节点应力评估方法

粟 京1，赵晓玲2，刘 刚3

（1.中国海洋石油总公司，北京 100028；2.大连船舶重工集团设计研究所，辽宁 大连 116005；3.大连理工大学 工业装备结构分析国家重点实验室，辽宁 大连 116024）

海洋工程焊接管节点受应力集中及复杂随机载荷的联合作用，容易发生疲劳破坏。为了提高焊接管节点结构疲劳寿命预测的准确性，文章以管壁厚方向上的一点作为疲劳评估点，提出了一种新的管节点结构应力计算方法。通过与国际上公开发表的疲劳试验数据进行比较，证明了文中方法应用于管节点结构的可行性及考虑壁厚方向应力梯度的有效性。基于数值计算，文中还提出了可用于T型管节点应力集中系数计算的参数公式，并对参数公式的精度进行了验证。

焊接管节点；应力集中系数；结构应力；应力梯度；疲劳寿命

0 引 言

焊接管节点在海洋工程领域有着极其广泛的应用。由于焊缝交线处存在严重的应力集中，加之焊接缺陷的影响，使得焊接管节点在各种随机环境载荷联合作用下焊缝位置应力状态非常复杂，疲劳破坏成为其主要的破坏形式之一[1]。在设计阶段，基于热点应力（Hot Spot Stress-HSS）的S-N曲线被广泛应用于海洋工程焊接管节点的疲劳寿命评估[2-3]。然而，对于受到多轴疲劳载荷作用的复杂焊接管节点，传统的疲劳评估应力计算方法仍存在一些问题。首先，目前的绝大部分工作均集中于特殊点处热点应力峰值的计算[4-7]而忽略了其沿管壁厚度方向及焊缝交线的分布规律；其次，研究中多采用壳单元对管节点进行模拟[8-11]，无法充分考虑焊趾尺寸对焊缝位置应力分布产生的影响。针对平板焊接结构的多轴疲劳寿命评估，刘刚等[12-13]提出了一种新的零点结构应力（Zero Point Structural Stress-ZPSS）法，并验证了其在平板焊接结构单轴及多轴疲劳强度评估中的优势。

基于上述讨论，为提高焊接管节点疲劳寿命预测的准确性，本文充分考虑裂纹扩展方向，以管壁厚度方向上非线性峰值应力为零的一点作为疲劳评估点，以该点的结构应力作为疲劳评估应力，将零点结构应力法进一步用于管节点的疲劳寿命评估。由于新方法疲劳评估点取为管壁外表面下方一点，可在一定程度上考虑应力梯度对疲劳寿命的影响；另外，该结构应力可直接通过有限元计算结果后处理得到，方便用于管节点的多轴疲劳寿命预测。

本文首先明确了管节点零点结构应力的定义，并给出了详细的零点结构应力计算流程；通过与公开发表的疲劳试验数据进行比较，对新方法应用于管节点疲劳强度评估的适用性和正确性进行了验证；为便于新方法在工程实际中的应用，本文基于大量的有限元数值计算，提出了T型管节点在各基本载荷作用下的零点结构应力集中系数参数方程，并对参数方程的精度进行了验证。

1 管节点零点结构应力定义

如图1所示，焊趾位置的局部切口应力σln可以分解为结构应力σss（包括弯曲应力σb和膜应力σm）和非线性峰值应力σnlp两部分。其中，σln随壁厚方向（x方向）的分布可通过精细有限元分析得到；σb、σm及σnlp的大小均可根据在壁厚方向的分布计算得到，如（1）-（3）式所示[14]。

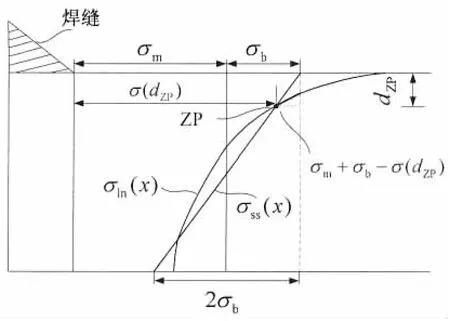
图2 零点位置及零点结构应力的定义Fig.2 ZP and ZPSS determination

结构应力σss用于平衡外加载荷，满足平衡方程；非线性峰值应力σnlp具有自平衡特性[5]，满足连续性方程。由于σnlp的自平衡特性，在壁厚方向上肯定存在一点，该点处σnlp的值为0，即σnlp=0。零点结构应力法中，将该点定义为“零点位置”（Zero Point-ZP），如图2所示；在该零点位置ZP，结构的真实切口应力等于结构应力的大小，因而可以认为没有受到焊趾引起的非线性峰值应力σnlp的影响，并将该点处的结构应力定义为“零点结构应力”（Zero Point Structural Stress-ZPSS）。参考热点应力法不考虑σln中σnlp的做法，在新的零点结构应力法中便可将ZPSS作为管节点疲劳强度评估的参考应力。得到结构应力分布曲线和局部切口应力分布曲线之后，ZP即可通过求解两条曲线的交点而得到。在ZP处，（3）式可以表示为

其中：dZP是ZP到管壁外表面的距离，从而可以得到求解ZP的表达式

当结构应力σss中只含有膜应力σm成分时，零点结构应力ZPSS与表面的热点应力值HSS相等；当σss中包含有弯曲应力σb成分时，由于σb沿板厚方向的应力梯度，ZPSS将略小于表面的HSS。因此，零点结构应力法可在一定程度上考虑应力梯度对疲劳寿命的影响。

本文引入美国机械工程师协会ASME[15]中应力分类线（Stress Classification Line-SCL）的概念，用于零点结构应力法中管节点疲劳评估应力的计算。如图3（a）所示，SCL定义为焊趾位置垂直于管壁表面沿管壁厚度方向的参考线，垂直于SCL的切口应力用于管节点零点结构应力ZPSS的计算。对任意极性角φ处，支管/主管上ZPSS最大值所在的平面很难确定，为此，计算过程中需遍历以SCL为轴线的360°所有面，计算任意平面上的ZPSS，选取最大的ZPSS及其对应的零点位置ZP和平面Δ作为最终结果，如图3（b）所示。当平面Δ同时经过支管的轴线时，计算得到的ZPSS仅包含垂直于焊缝的应力成分；否则，计算的ZPSS还会包含切应力成分，在这种情况下，剪切应力对管节点疲劳寿命的影响也会同时考虑在内。

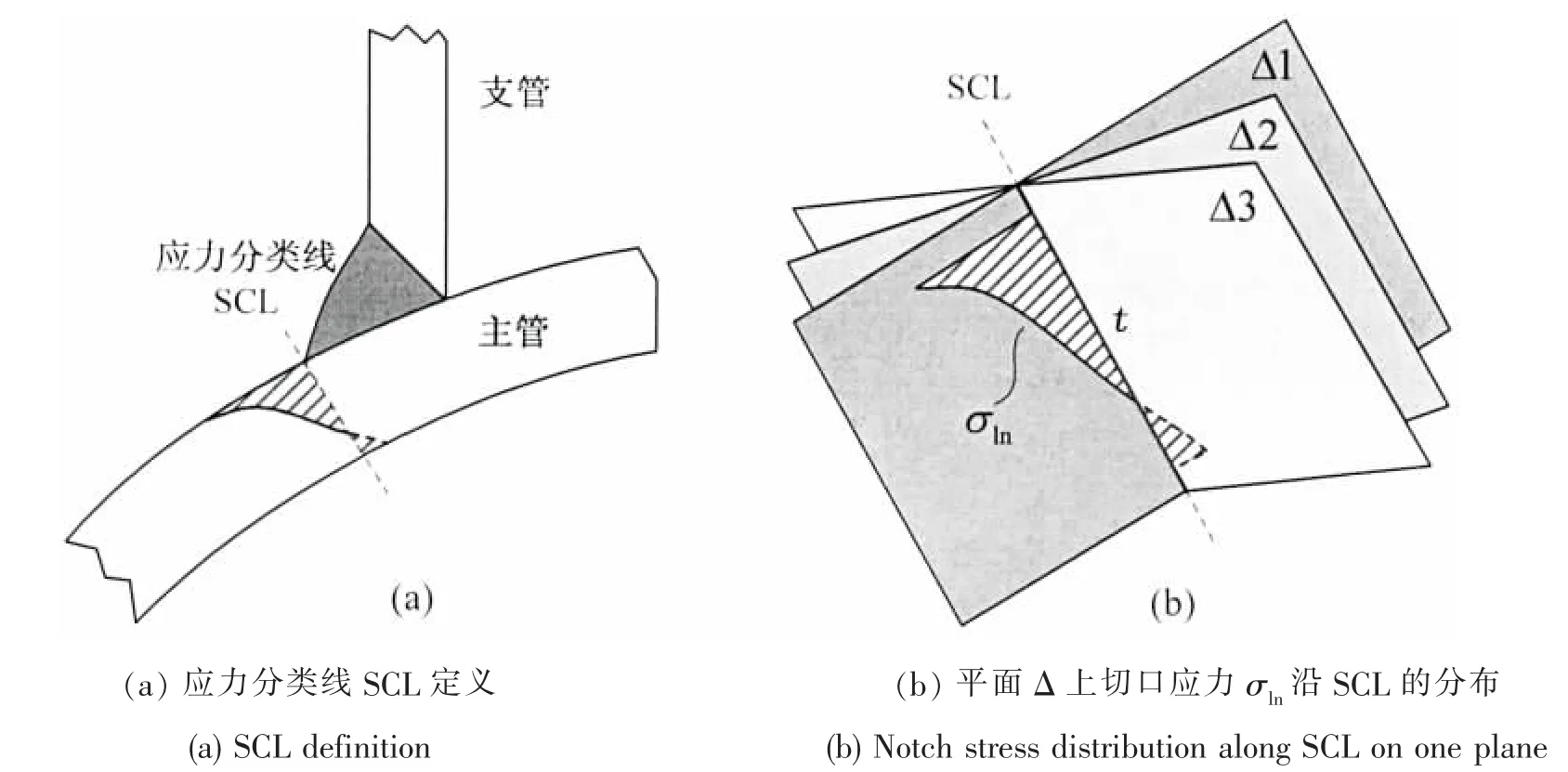
图3 管节点零点结构应力计算Fig.3 ZPSS calculation of tubular joints

特定极性角处，管节点零点结构应力的计算流程如下：

（1）提取焊趾端面沿管壁厚度方向SCL上所有节点的应力张量；

（4）按照（1）～（3）的过程，计算以SCL为轴线的所有面上的ZP及ZPSS，比较得到ZPSS的最大值及对应的ZP。

2 管节点零点结构应力计算

以图4中所示的T型管节点为例，将零点结构应力法用于其疲劳评估应力的计算。表1给出了管节点的几何参数。为更加准确地考虑焊缝尺寸对管节点应力分布产生的影响，采用三维的20节点块体单元对管节点的支管、主管及焊缝进行详细建模[16]，如图5所示；且为验证零点结构应力法在管节点中的适用性和可行性，将轴向载荷（Axial loading-AX）、面内弯曲载荷（In-plane bending-IPB）、面外弯曲载荷（Out-of-plane bending-OPB）等三种基本载荷作用下的零点结构应力法的计算结果与常用的热点应力法计算结果进行了对比。

表1 管节点几何参数Tab.1 Geometric parameters

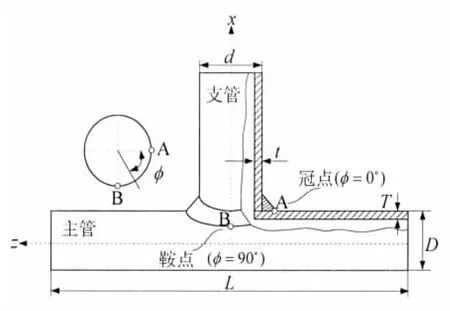
图4 T型焊接管节点的外形尺寸Fig.4 Dimensions of a welded tubular T-joint

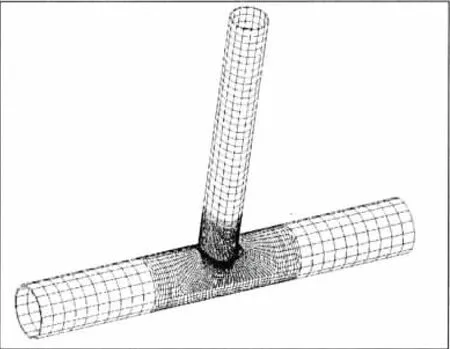
图5 T型焊接管节点整体有限元模型Fig.5 Full FE model of a welded tubular T-joint

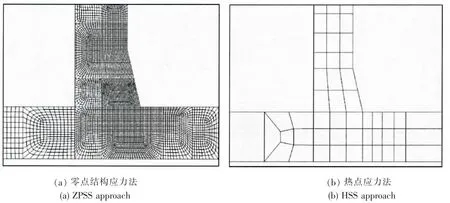
图6 焊趾附近的网格局部放大图Fig.6 Close-up view of the mesh around the weld toe

经过收敛性测试，零点结构应力法中焊趾附近网格尺寸定义为0.025tb和0.025tc沿焊缝交线共划分为64个单元；热点应力法中在焊趾处沿管壁厚度方向划分为3个单元，沿焊缝交线划分为32个单元，图6（a）、（b）所示分别为两种方法对应的焊趾附近局部网格放大图。

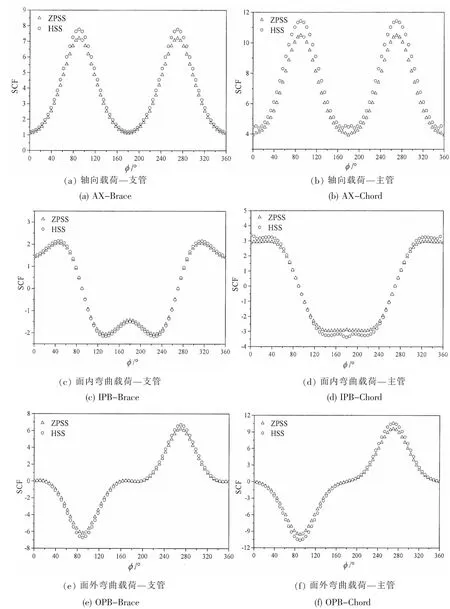
图7 分别采用HSS和ZPSS法计算应力集中系数沿焊缝交线的分布Fig.7 SCFs distribution along the intersection calculated by HSS and ZPSS methods

将热点应力HSS法和零点结构应力ZPSS法的应力集中系数分别表示为SCF和SCFZP，计算结果如图7所示。由图中可以看出，沿焊缝360°交线ZPSS法计算得到的SCFZP绝对值始终比HSS方法计算得到的SCF要小。这是因为在外加载荷作用下，为保持管节点各构件在焊缝交线处的连续性及变形协调，管壁在焊趾位置会产生局部弯曲变形，从而产生弯曲应力分量σb，由于壁厚方向应力梯度的影响，计算得到的ZPSS通常比管壁外表面处的结构应力略小（见图2）。这种现象可认为是零点结构应力法对弯曲应力的一种折减，从而可以在一定程度上考虑管壁厚度方向上应力梯度对管节点疲劳寿命的影响。如图7（b）所示，轴向拉伸载荷作用下，主管上计算得到的ZPSS与HSS差异的最大值出现在鞍点位置，这是由于在该点处的局部弯曲效应最显著。对于其他载荷类型，可由该原因得到同样类似的现象。

3 零点结构应力法精度验证

为验证零点结构应力法用于T型管节点疲劳寿命评估的有效性和计算精度，作者选取来自英国海上钢铁研究项目（UKOSRP-I）[17]的32个焊接管节点，对其进行数值计算分析。表2[18]中详细列出了32个管节点的几何参数、外加载荷类型、测试得到的HSS以及疲劳失效寿命N，表中同时给出了本文计算得到的ZPSS以及ZPSS与HSS的比值。图8将试验测得的T型管节点HSS与有限元数值计算得到的ZPSS进行了比较。

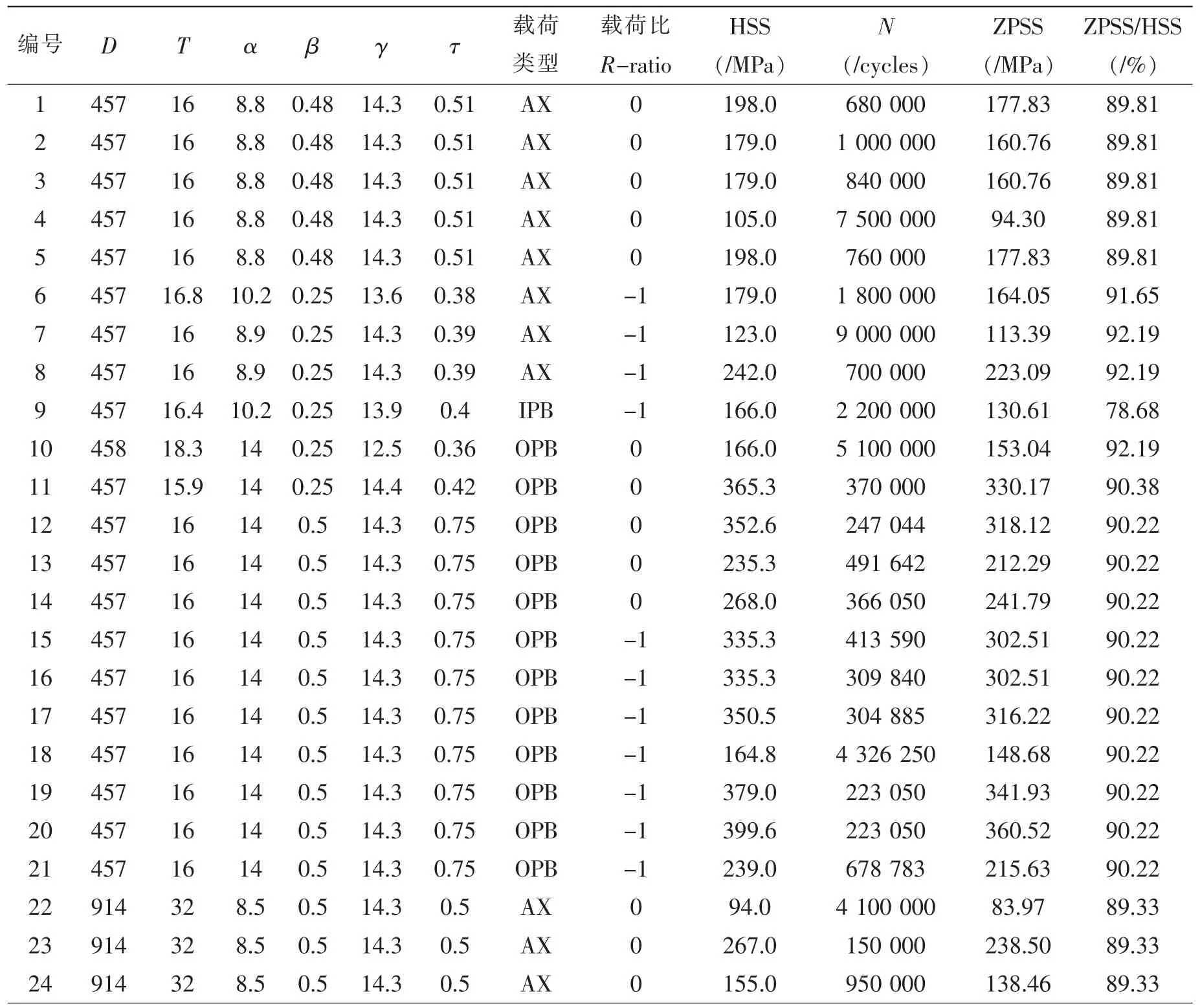
表2 T型管节点[18]参数及试验测量的HSS和计算的ZPSSTab.2 Geometric parameters,measured HSS and calculated ZPSS of the tubular T-joints[18]

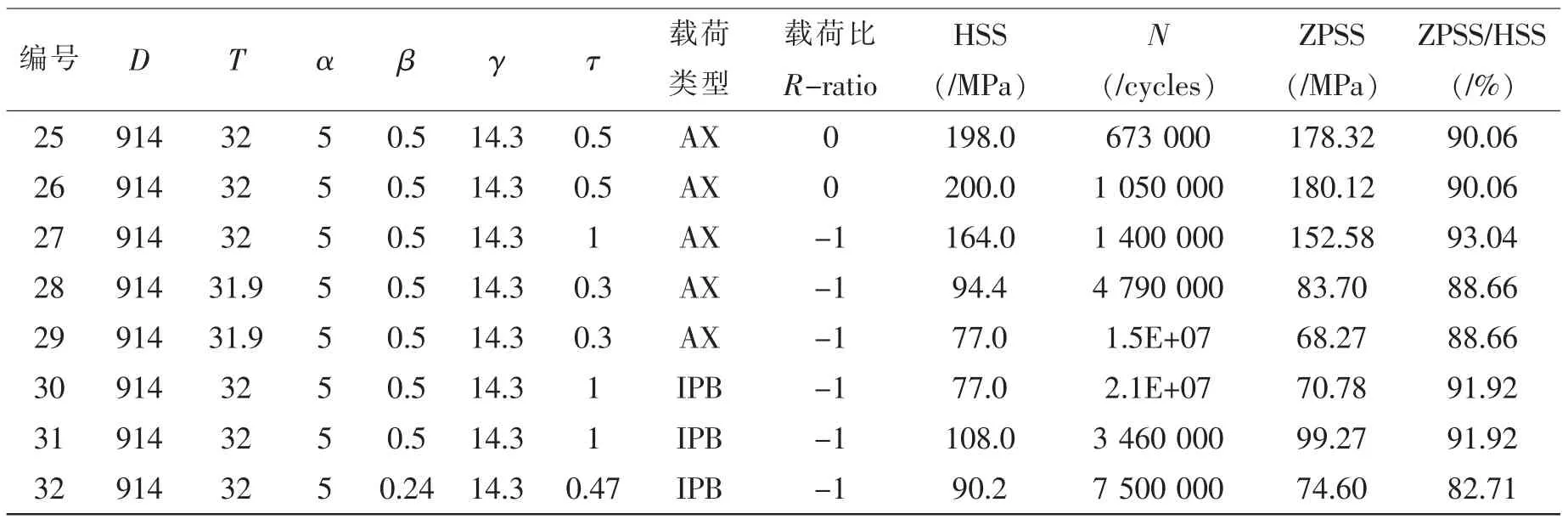
续表2

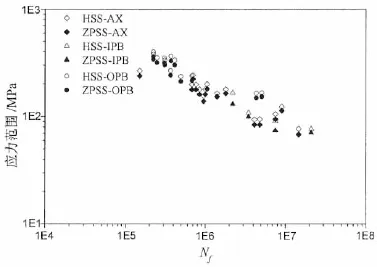
图8 T型管节点测量HSS与计算ZPSS的比较Fig.8 Stress comparison between the measured HSS and calculated ZPSS of tubular T-joints

表3 T型管节点的无量纲参数Tab.3 Non-dimensional geometric parameters of tubular T-joints

由图8可以看出，两种方法的计算结果总体上来看非常接近，分布规律相似，这说明了ZPSS用于管节点的可行性和正确性。同时，对所有载荷作用下的管节点，ZPSS法的计算结果始终略小于HSS法计算结果，这主要是由于ZPSS法中考虑了管壁厚度方向弯曲应力的应力梯度，而HSS法直接选取了结构表面处插值得到的结构应力。需要注意，虽然HSS与ZPSS两种方法对应的疲劳评估应力计算点不同，但二者的目的均是评估热点处的疲劳强度。ZPSS法的计算结果在某种程度上可看作是对HSS法计算结果的一种修正，这种修正即是为了考虑管壁厚度方向应力梯度对疲劳寿命的影响。在ZPSS法中，在结构表面以下一定深度处取计算点，其思想类似于切口应力法中的点法[19-20]。理论上HSS与ZPSS两种方法的计算结果应该比较接近，但ZPSS法应该更合理。另外，如表2所示，ZPSS与HSS之间的比值在大部分情况下为90%，这说明ZPSS法可以考虑管壁厚度方向应力梯度对管节点疲劳寿命的影响，因而比传统的HSS法具有更高的精度。

4 T型管节点零点结构应力集中系数参数方程

有限元计算结果表明，零点结构应力集中系数SCFZP沿管节点极性角φ的分布规律是其几何参数及外加载荷共同影响的结果。为便于零点结构应力法在实际工程中的应用，作者基于对各基本载荷作用下数值计算结果的分析，提出了以无量纲参数为变量的SCFZP参数公式。数值计算过程中，主管外径取值为D=600 mm，支管长度取值为l=3 000 mm，通过对600组不同几何参数的T型焊接管节点（见表3）进行计算，得到了各基本载荷作用下沿管节点焊缝交线的应力分布状态。

由图7中可以看出，管节点在不同类型载荷作用下其应力分布状态差异较大，因此对不同载荷类型作用下的应力分布规律分别进行考虑。由图7同时可以看出，零点结构应力集中系数SCFZP沿着支管/主管交线的分布与极性角φ之间关系非常复杂，SCFZP随极性角φ的分布可视为一个周期内的周期函数。容易得知，任何周期函数都可以用由正弦函数和余弦函数构成的无穷级数（即傅里叶级数）来表示。本文通过收敛性测试，选择三阶傅里叶级数作为拟合SCFZP随极性角φ分布规律的基本形式，如（6）式所示。

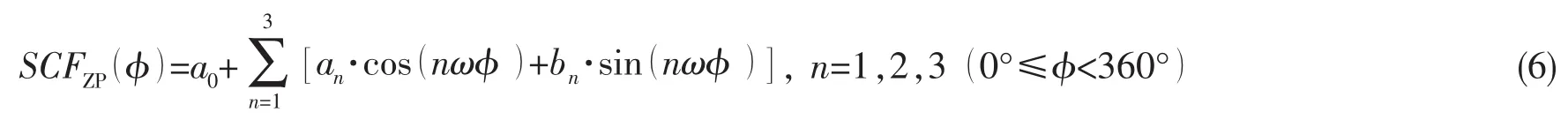
其中：a0、an、bn以及ω是傅里叶级数的系数，φ表示管节点沿着焊缝的极性角。

进一步基于各基本载荷作用下的600组数值计算结果，利用数值分析软件通过逐步回归算法对（6）式中的系数a0，a1，b1，a2，b2，a3，b3以及ω进行拟合，最终得到了以无量纲参数为输入变量的SCFZP参数公式，见附录A。对参数公式适用范围内的任意T型管节点，利用该组公式可直接计算其SCFZP沿焊缝交线的分布规律，得到SCFZP极值出现的位置和大小。

为验证SCFZP参数公式的计算精度，本文对参数公式的计算结果进行了误差分析。分析过程中，对任意尺寸的T型管节点，选取沿焊缝交线的SCFZP最大值用于误差计算。参数公式计算得到的SCFZP误差可由（7）式定义为

其中：SCFZP-PAR及SCFZP-FEM分别表示SCFZP的公式计算结果和有限元法计算结果。

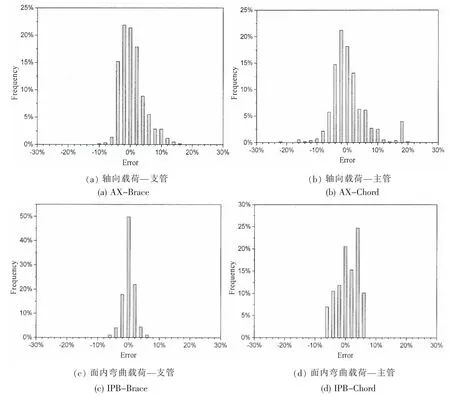
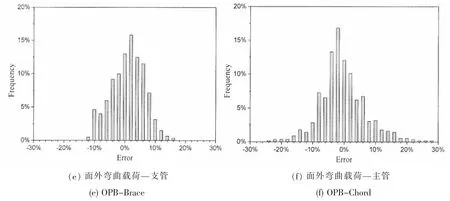
图9 SCFZP参数公式计算结果的误差频率直方图Fig.9 Histograms showing percentage errors of SCFZPparametric equation predictions

图9所示为本文所提出的SCFZP各参数公式误差频率分布直方图，图中每一竖列的误差分布范围为横轴上给定的中间值±1%。由上图可以看出，各直方图中误差的分布均以峰值处为中心，向两侧迅速减小为0；峰值附近的误差概率最高，且误差的整体分布范围较窄，这说明了数值回归参数方程SCFZP计算结果与有限元计算结果的一致性。SCFZP参数公式计算结果的最大误差约为28%，出现在面外弯曲载荷作用下的主管上，如图9（f）所示。SCFZP的参数公式计算结果的误差绝大部分分布在-10%到10%的范围内，图9（a）-（d）中的SCFZP计算误差主要分布在-5%到5%之间。以上的误差分析结果表明，本文拟合得到的SCFZP参数公式精度较高，可用于工程实际。

5 结 论

（1）提出了焊接管节点零点结构应力法的定义，通过与热点应力法计算结果比较，验证了零点结构应力法在管节点应力分析中的适用性和可行性。

（2）通过与国际疲劳试验数据对比分析，验证了管节点零点结构应力法的正确性以及考虑壁厚方向应力梯度的有效性。

（3）基于大量数值计算结果，提出了零点结构应力集中系数参数方程，可对任意基本载荷作用下支管/主管焊缝交线上的SCFZP进行计算，便于工程应用。

[1]Chang E,Dover W.Parametric equations to predict stress distributions along the intersection of tubular X and DT-joints [J].International Journal of Fatigue,1999,21(6):619-635.

[2]American Petroleum Institute.Recommended practice for planning,designing and constructing fixed offshore platforms load and resistance factor design[S].1993.

[3]Department of Energy.Background to new fatigue design guidance for steel welded joints in offshore structures[S].1984.

[4]Kuang J,Potvin A,Leick R.Stress concentration in tubular joints[C]//Offshore Technology Conference.Houston,TX, 1975.

[5]Wordsworth A,Smedley G P.Stress concentrations at unstiffened tubular joints[C].Cambridge(UK):1978.

[6]Wordsworth A.Stress concentration factors at K and KT tubular joints[J].Institution of Civil Engineers,Thomas Telford Ltd,1981:59-69.

[7]Smedley P,Fisher P.Stress concentration factors for simple tubular joints[C].Edinburgh,UK:1991.

[8]Chang E,Dover W.Prediction of stress distributions along the intersection of tubular Y and T-joints[J].International Journal of Fatigue,1999,21(4):361-381.

[9]Morgan M,Lee M.Prediction of stress concentrations and degrees of bending in axially loaded tubular K-joints[J].Journal of Constructional Steel Research,1998,45(1):67-97.

[10]Morgan M,Lee M.Parametric equations for distributions of stress concentration factors in tubular K-joints under out-ofplane moment loading[J].International Journal of Fatigue,1998,20(6):449-461.

[11]Lotfollahi-Yaghin M A,Ahmadi H.Effect of geometrical parameters on SCF distribution along the weld toe of tubular KT-joints under balanced axial loads[J].International Journal of Fatigue,2010,32(4):703-719.

[12]Liu G,Liu Y F,Huang Y.A novel structural stress approach for multiaxial fatigue strength assessment of welded joints[J]. International Journal of Fatigue,2014,63:171-182.

[13]刘 刚,刘英芳,黄 一.焊接结构多轴疲劳寿命预测结构应力法[J].船舶力学,2014,18(10):1220-1227. Liu Gang,Liu Yingfang,Huang Yi.Structural stress approach for multiaxial fatigue life estimation of welded structures[J]. Journal of Ship Mechanics,2014,18(10):1220-1227.

[14]Hobbacher A.Fatigue design of welded joints and components[M].IIW Document XIII-1539-96/XV-845-96,1996.

[15]Boiler A,Committee P V.Rules for construction of pressure vessels:Alternative rules for construction of high pressure vessels.Division 2[M].American Society of Mechanical Engineers,2004.

[16]Lie S,Lee C,Wong S.Modelling and mesh generation of weld profile in tubular Y-joint[J].Journal of Constructional Steel Research,2001,57(5):547-567.

[17]Peckover R,Fraser R,Grisp H,et al.The United Kingdom offshore steel research project[M].Phase I:Final Report.Offshore Technology Report OTH 88 282.HMSO,1989.

[18]Background to new fatigue guidance for steel joints and connections in offshore structures[M].Offshore Technology Report OTH 92 390(HSE).England:Health and Safety Executive,1995.

[19]Susmel L.Three different ways of using the Modified Wöhler Curve Method to perform the multiaxial fatigue assessment of steel and aluminium welded joints[J].Engineering Failure Analysis,2009,16(4):1074-1089.

[20]Susmel L.Modified Wöhler curve method,theory of critical distances and Eurocode 3:A novel engineering procedure to predict the lifetime of steel welded joints subjected to both uniaxial and multiaxial fatigue loading[J].International Journal of Fatigue,2008,30(5):888-907.

附录A

A.1 AX载荷作用下零点结构应力集中系数SCFZP参数方程

（1）支管

（2）主管

A.2 IPB载荷作用下零点结构应力集中系数SCFZP参数方程

（1）支管

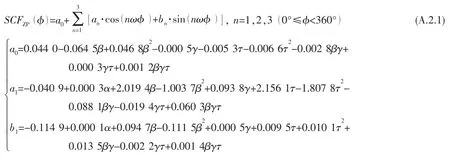
（2）主管

A.3 OPB载荷作用下零点结构应力集中系数SCFZP参数方程

（1）支管

（2）主管

注意：

（1）所有的参数方程应在下述范围内使用：

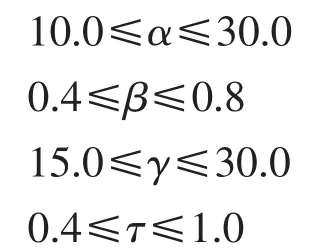
（2）φ的单位为度。

A new method for stress analysis of tubular joints in offshore platform

SU Jing1,ZHAO Xiao-ling2,LIU Gang3
(1.China National Offshore Oil Corporation,Beijing 100028,China;2.Dalian Shipbuilding Industry Engineering and Research Institute,Dalian 116005,China;3.State Key Laboratory of Structural Analysis for Industrial Equipment, Dalian University of Technology,Dalian 116024,China)

Fatigue damage in welded tubular joints is almost unavoidable due to combined effect of stress concentration and random stresses.To improve accuracy of fatigue life estimation of welded tubular joints,a new structural stress approach for tubular joints is proposed,where a point below the outer surface along the wall thickness direction is adopted as the fatigue assessment point.The applicability and correctness of the new method for fatigue strength assessment of tubular joints,as well as its effectiveness in considering the stress gradient along the wall thickness,are verified by comparing the numerical results with published experimental data of fatigue tests.Based on finite element analysis,parametric equations are derived for calculating stress concentration factors at all angular positions along the intersection of tubular T-joints.The accuracy of the parametric equations is finally validated.

welded tubular joints;stress concentration;structural stress;stress gradient;fatigue life

TG405

A

10.3969/j.issn.1007-7294.2016.07.012

1007-7294（2016）11-1449-13

2016-07-08

国家自然科学基金项目（51179027，51221961，51379031）；国家973计划项目（2011CB013704）

粟 京（1959-），男，硕士,高级工程师,E-mail：sujing@cnooc.com.cn；刘 刚（1975-），男，教授，博士生导师，E-mail:liugang@dlut.edu.cn。