考虑铺设残余变形影响的管道屈曲分析
谢 鹏,岳前进,赵 岩
(大连理工大学 工业装备结构分析国家重点实验室,辽宁大连116023)
考虑铺设残余变形影响的管道屈曲分析
谢 鹏,岳前进,赵 岩
(大连理工大学 工业装备结构分析国家重点实验室,辽宁大连116023)
文章基于壳单元建立了精细的托管架—管道相互作用模型,模拟了S型管道铺设过程,研究了铺设过程中管道的塑性变形分布,评价了铺设残余塑性变形对管道屈曲压力的影响。研究结果表明在深水S型铺设中,管道会发生明显残余塑性变形,并削弱管道的后续屈曲承载能力。
S型铺管法;管道;有限元分析;塑性变形;屈曲
0 引 言
S型铺管法是海底管道铺设中的一种重要方法,铺管系统主要由铺管船船体、张紧器和托管架三部分组成,因铺设时其线型类似S而得名[1-2]。铺管作业时,预制的短节管道在铺管船焊站上经焊接制成连续管道后,通过无损检测、张紧器,沿托管架滑入水中。随着铺设水深的增加,管道在上弯段承受的弯曲、轴向拉力和托辊反力增大,不可避免地发生塑性变形[3-5]。Xie等[6]基于模型实验研究,确定了铺设过程中上弯段管道任意截面上发生局部塑性变形时的应力分布状态。在该种状态下,管道首先在截面上受拉的一侧达到屈服极限,而靠近中性轴的钢材依旧处于弹性范围内,尚具有继续承载外部荷载的能力。随着外部荷载的增加,管道的塑性区向中性轴扩展,直至达到完全塑性状态。在受压区一侧,托辊支撑引起管道发生应变集中,导致管道发生不规则变形。当管道铺设到海底后,在外压的作用下,管道内产生新的应变并与残余变形叠加,引起管道发生屈曲失效,在现有的设计规范中这是没有考虑的[7]。
Palmer[8]于1975年首次揭示了在海底管道铺设过程中管道发生局部屈曲失稳,并会沿管道轴线方向传播。Langner[9]研究了管道的屈曲发生及传播的最小压力。Dama[10]通过试验和数值模拟研究了受损管道在内压和弯矩作用下的承载力,为受损管道的局部屈曲分析提供了可借鉴的方法。Toscano等[11]基于有限元模型分析,研究了深水海底管道整体式止屈器的穿越压力和机理。Netto[12]开展了使用止屈器防止屈曲进行传播的试验,并基于试验结果拟合了经验公式。张日曦等[13]分析了初始椭圆度对小径厚比深水管道屈曲临界压力的影响。余建星等[14]基于非线性有限元方法和模型实验验证,研究了不同尺寸的初始椭圆缺陷对不同径厚比管道压溃压力的影响。综上所述,目前学者们对海底管道承载能力的研究大多数是为了建立屈曲的临界压力和管道椭圆度之间的关系,以及防止屈曲传播方面,而尚未有针对铺设过程中残余塑性变形对管道屈曲压力影响的研究。本文基于对S型海底管道铺设过程的模拟,计算了管道的残余变形及其对临界屈曲压力的影响。
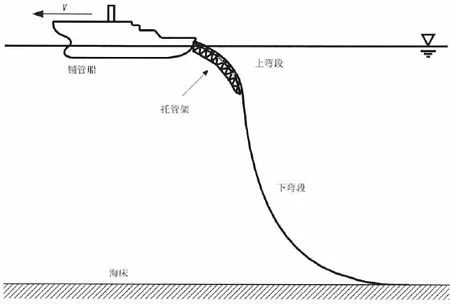
图1 S型海底管道铺设Fig.1 S-lay operation
1 S型海底管道铺设过程分析
以1 500 m水深铺设24英寸管道为例,采用Abaqus软件建立三维的弹性托管架模型和基于壳单元的管道模型,模拟管道从托管架滑下的动力过程,分析管道的应变历史及铺设残余应变分布。
1.1 S型海底管道铺设的有限元分析
托管架的曲率半径为110 m,由三节空间桁架结构组成。托管架杆件主要承受轴向压力作用,在模型中采用Pipe31单元模拟。该单元使用铁木辛克梁模型,能够承受轴向压力、允许发生横向剪切变形,可以准确模拟托管架结构的受力情况。托管架上部的托辊采用“V”型结构模拟,比较真实的模拟原型中管道和托辊的受力方式。托管架的A型支架(A-frame)起到提升托管架纵向刚度的作用,需要承受一定的弯矩,因此使用B31梁单元模拟。节间连杆(puppiece)是托管架节与节之间的连接构件,在托管架的节与节之间传递弯矩作用,采用B31梁单元模拟。托管架的有限元模型总图和单元分布如2所示。
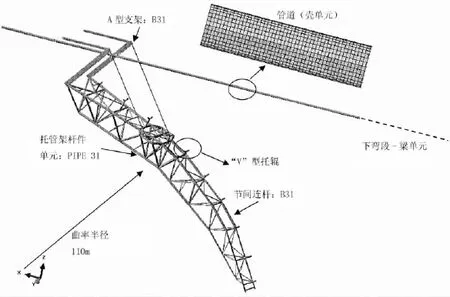
图2 S型海底管道铺设的有限元模型Fig.2 S-lay operation FEM model
1.2 管道的材料属性
管道分为上弯段和下弯段两个部分。上弯段管道采用精细的壳单元S4R模拟,该单元可以考虑管道的大变形和非线性材料属性,准确模拟管道和托辊的接触行为,易于获得管道截面上的局部变形和应变分布状态。上弯段管道长230 m,能够覆盖整个托管架,共包括9 000个单元。下弯段管道是上弯段管道的荷载边界条件,在模型中起到为上弯段提供荷载的作用。为了减小计算量、提高计算效率,下弯段管道采用B31梁单元模拟。下弯段管道长2 300 m,共2 300个单元。B31梁单元能够合理的模拟管道在下弯段的线型和质量。管道在上弯段的末端进行“壳—梁”单元的自由度耦合连接。管道的材料属性采用非线性的Ramberg-Osgood模型[15-16],该模型能够合理地描述管道的塑性变形,其表达式如下式所示:

其中:E为弹性模量,ε是材料应变,σ是材料应力,σy是屈服强度,ν是泊松比,A和B是描述材料塑性变形的硬化参数。该模型参数见表1。

表1 管道的几何和材料参数Tab.1 Pipe geometry and material parameters
1.3 边界条件和载荷步
托管架在主铰接点和A-frame的连接点处固定;管道在初始构型中水平放置,并逐步施加如下荷载。首先,在水平管道中施加轴向拉力,模拟铺设过程中张紧器和铺管船推进器对管道产生的水平方向拉力作用。其次,对于整个系统施加重力荷载,使管道逐步下垂,变形为S型。上弯段管道首先与托管架接触,下弯段管道与海底接触。最后,当管道完全变成S型后,再对管道施加强迫位移,使管道沿着托管架向下滑动,模拟管道的铺设过程。
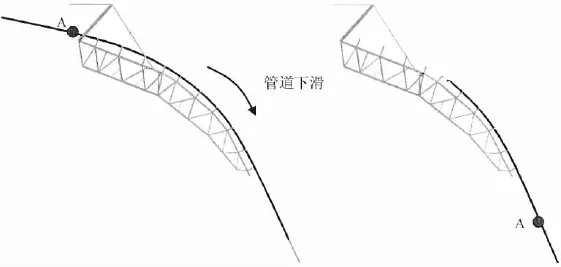
图3 管道从托管架上下滑过程模拟Fig.3 Simulation of pipe sliding downward the stinger
1.4 计算结果
1.4.1 管道在托管架上的塑性变形分布
管道在托管架上受到托辊反力的集中荷载作用,发生塑性变形,应变云图如图4所示。在管道的最外层拉应变较大,在受到托辊挤压的一侧,管道承受压应变。由于托辊与管道的接触面积并不规则,在托辊和管道的挤压位置应变不均匀,发生应变集中现象。
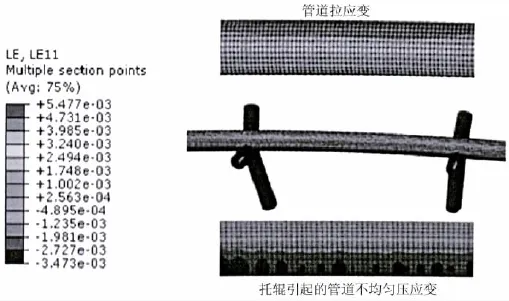
图4 上弯段管道的应变分布状态Fig.4 Overbend residual strain distribution
1.4.2 管道从托管架上滑落过程的应变历史
在铺设过程中,管道从托管架上的第一个托辊开始下滑,依次经过托管架上的所有托辊。以图3中A截面的最大应变变化历史如图5所示。结果显示,管道应变在下滑的过程中并不均匀,随着托辊的位置发生变化。经过托辊支撑时,截面应变明显增大;在随后的相邻托辊之间,管道应变又减小。这主要是因为托辊反力使管道承受的局部弯矩增大,管道发生应变集中。
1.4.3 管道的残余塑性变形
管道在从托管架下滑的过程中经历了一系列的循环应变作用,如图6所示。起始时,管道应变增加,材料进入塑性阶段。管道逐步从托管架上滑落,在托辊反力较小的3号托辊上应力、应变下降,随着管道继续下滑,又继续上升。当管道从托管架上滑落后,会沿着接近竖直的线型逐步滑至海底,直到与海床接触。在这一阶段,由于管道脱离了托管架的支撑,承受的弯矩减小,弯曲应变也逐步减小,如图中的BC阶段。当管道经过下弯段中的反弯点后,逐步承受压应变,该点的应变开始反向增大,但塑性变形一直存在,不会消失。
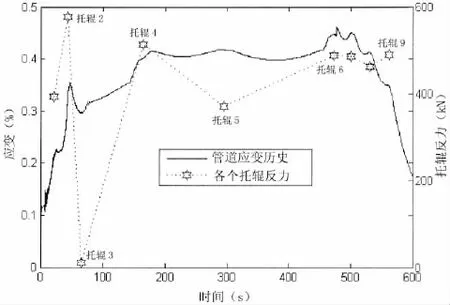
图5 管道下滑过程中的应变时程和托辊反力Fig.5 Pipe strain history during sliding downward the stinger and roller force distribution
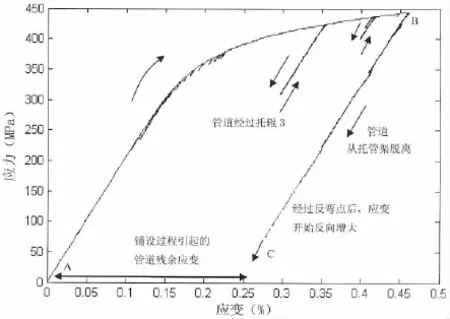
图6 管道下滑过程中的应力应变历史Fig.6 Pipe stress strain history during the sliding down process
2 含残余变形管道的屈曲分析
含有铺设塑性变形的管道到达海底后,残余变形并不会消失,而是在管道外压荷载的作用下,与新产生的变形相叠加,削弱管道抵抗屈曲的能力。
2.1 理想管道的塑性屈曲压力计算公式
Kyriakide[17]从管道的受力微元出发,推导了管道的塑性临界屈曲压力,如计算公式(2)-(4)所示:

其中:Pc是管道的临界曲压力,t是管道的壁厚,R是管道的半径,Et是切线弹性模量,Es是割线弹性模量,υ是泊松比。
2.2 含塑性变形管道的临界屈曲压力
公式(2)-(4)虽然可以计算无缺陷管道在外压荷载下的临界塑性屈曲压力,却无法考虑不规则残余塑性变形对管道临界屈曲压力的影响。有些学者研究了椭圆率对管道屈曲行为的影响,但在海底管道铺设过程中管道的塑性变形并不是椭圆的。其大小和分布受到托辊反力、管道直径、管道壁厚的影响,难以建立精确的解析表达式[18-19]。本文以含有铺设残余塑性变形的管道作为屈曲分析的初始形状,在管道外层施加外压进行屈曲分析,变形后的管道位移云图如图7所示。
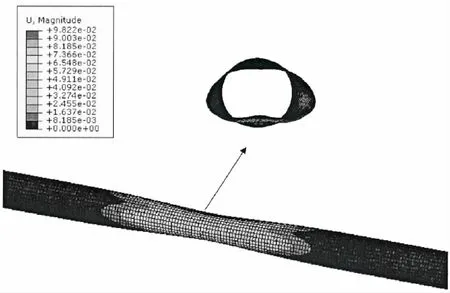
图7 含塑性变形管道屈曲时的位移云图Fig.7 Displacement contour during the plastic deformed pipe buckling
管道在外压荷载作用下发生局部屈曲,并逐步向两端扩展,变形过程如图8所示。横坐标是管道的椭圆率(公式(5)),纵坐标是管道的外压。开始时,管道在外压作用下椭圆率增加,随着变形的增大,管道的承载能力逐步降低,直至完全丧失。从图中可以看出管道的临界屈曲压力是35.8 MPa,按照公式(2)计算无损伤管道的临界屈曲压力是53.14 MPa。由此可见,残余塑性变形削弱了管道的屈曲承载能力。

其中:f0是管道的椭圆率,Dmax是变形后管道的最大直径,Dmin是最小直径,D是初始直径。
3 结 语
本文基于有限元分析,模拟了S型海底管道的铺设过程,计算了管道在经过托管架后的残余塑性变形分布以及其对后续承载能力的影响,得到如下结论:
(1)在铺设过程中,管道在上弯段发生塑性变形,应变分布不均匀。在托辊上受拉的一侧,管道拉应变较大。在受到托辊挤压的一侧,体现为压应变。由于托辊的集中反力作用,管道产生局部应变集中现象,变形不规则。
(2)管道的残余塑性变形会削弱管道的屈曲承载能力,引起管道屈曲压力的大幅下降,在深水S型海底管道铺设中应当予以考虑。
[1]Palmer A C,King R A.Subsea pipeline engineering[M].PennWell Books,2004.
[2]Heerema E.Recent achievements and present trends in deepwater pipe-lay systems[C].Offshore Technology Conference, 2005.
[3]Perinet D,Frazer I.Strain criteria for deep water pipe laying operations[C].Proceedings of the 40th Offshore Technology Conference.OTC,2008.
[4]Torselletti E,Vitali L,Levold E,et al.Submarine pipeline installation JIP:Strength and deformation capacity of pipes p assing over the S-lay vessel stinger[C].25th International Conference on Offshore Mechanics and Arctic Engineering, 2006:227-235.
[5]Torselletti E,Vitali L,Bruschi R,et al.Submarine pipeline installation joint industry project:Global response analysis of pipelines during S-laying[C].25th International Conference on Offshore Mechanics and Arctic Engineering,2006:217-225.
[6]Xie P,Yue Q,Palmer A C.Cyclic plastic deformation of overbend pipe during deepwater S-lay operation[J].Marine Structures,2013,34:74-87.
[7]Veritas D N.DNV-OS-F101:Submarine pipeline systems[Z].2012.
[8]Palmer A C,Martin J H.Buckle propagation in submarine pipelines[J].Nature,1975,254(5495):46-48.
[9]Langner C.Buckle arrestors for deepwater pipelines[C].Offshore Technology Conference,1999.
[10]Dama E,Karamanos S,Gresnigt A.Failure of locally buckled pipelines[J].Journal of Pressure Vessel Technology,2007, 129(2):272-279.
[11]Toscano R G,Mantovano L O,Amenta P M,et al.Collapse arrestors for deepwater pipelines.Cross-over mechanisms[J]. Computers&Structures,2008,86(7):728-743.
[12]Netto T,Estefen S.Buckle arrestors for deepwater pipelines[J].Marine Structures,1996,9(9):873-883.
[13]张日曦,张 崎,黄 一.小径厚比深水管道的压溃屈曲研究[J].船舶工程,2012,34(004):94-97. Zhang Rixi,Zhang Qi,Huang Yi.Collapse buckling study on deepwater pipelines with small radius-thickness ratio[J]. Ship Engineering,2012,34(004):94-97.
[14]余建星,李智博,杜尊峰等.深海管道非线性屈曲理论计算方法[J].海洋工程,2013,(01):54-60. Yu Jianxing,Li Zhibo,Du Zunfeng,et al.Theoretical calculation method of the nolinear buckling of deepsea pipes[J].O-cean Engineering,2013,(01):54-60.
[15]周家泽.工程材料弹塑性应力应变模型分析[J].武汉科技学院学报,2003,(06):42-45. Zhou Jiaze.Sress and strain analysis for elastic and plastic model of engineering materials[J].Journal of Wuhan University of Science and Engineering,2003,(06):42-45.
[16]白 宁,赵冬岩.海底管道弯矩—曲率形式的 Ramberg-Osgood方程参数计算[J].中国海洋平台,2012,26(6):16-20. Bai Ning,Zhao Dongyan.Parameters calculation of ramberg-osgood equation in moment-curvature form for offshore pipeline [J].China Offshore Platform,2012,26(6):16-20.
[17]Kyriakides S,Corona E.Mechanics of offshore pipelines:volume 1 buckling and collapse[M].Access Online via Elsevier, 2007.
[18]Vitali L,Torselletti E,Spinazzeè M,et al.Bending capacity of pipes subject to point loads[C].ASME 2003 22nd International Conference on Offshore Mechanics and Arctic Engineering,2003:675-686.
[19]Yun H D,Peek R R,Paslay P R,et al.Loading history effects for deep-water s-lay of pipelines[J].Journal of Offshore Mechanics and Arctic Engineering,2004,126(2):156.
Pipe buckling analysis considering the installation residual deformation
XIE Peng,YUE Qian-jin,ZHAO Yan
(State Key Laboratory of Structural Analysis for Industrial Equipment,Dalian University of Technology,Dalian 116023,China)
The present paper analyzes the pipe stress-strain history during the S-lay operation with detailed Stinger-Pipeline FEM model,and evaluates the buckling effects of the plastic deformation.The research results show that in deep-water S-lay operation,the laying process results in obvious plastic deformation to pipeline,which reduces the buckling capacity of the pipeline.
S-lay;pipe;Finite Element Analysis;plastic deformation;buckling
P751
A
10.3969/j.issn.1007-7294.2016.07.011
1007-7294(2016)11-1441-08
2016-06-18
863项目“深水海底管道铺设技术研究”资助(2006AA09A105);973项目“深海水下油气输送系统可靠性理论研究”资助(2014CB046803)
谢 鹏(1987-),男,博士研究生,E-mail:xiepeng@mail.dlut.edu.cn;岳前进(1958-),男,教授,博士生导师。

