电磁力控制翼型三维绕流场特性的数值研究

尹纪富，林忠义，李 巍，尤云祥，胡天群

（1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.中交疏浚技术装备国家工程研究中心，上海 201208；3.嘉兴南阳职业技术学院，浙江 嘉兴 314003）

电磁力控制翼型三维绕流场特性的数值研究

尹纪富1，2，林忠义3，李 巍1，尤云祥1，胡天群1

（1.上海交通大学 海洋工程国家重点实验室，上海 200240；2.中交疏浚技术装备国家工程研究中心，上海 201208；3.嘉兴南阳职业技术学院，浙江 嘉兴 314003）

在弦长雷诺数ReL=2.97×106下，采用脱体涡模拟方法对弱电解质中电磁力作用下翼型绕流场特性进行了数值模拟，研究了电磁力作用控制翼型失速攻角时绕流场中三维流动特性及失速问题的规律和机理。结果表明：电磁力作用可有效改善翼型周围的流场结构，显著减小翼型绕流场三维特性，并使翼型表面流体动能增加，当电磁力作用足够大时，其表面涡量转变为正向涡量。同时，电磁力作用可增加翼型升力，减小阻力，显著减小升阻力脉动特性，提高翼型升阻比，还可以显著延缓翼型失速特性，增加失速攻角，提高工作性能。

电磁力；翼型绕流；失速；数值模拟

0 引 言

翼型结构在船舶工程中应用广泛，在其随船舶以一定攻角航行的过程中，翼型表面的流动分离会使其升力减小而阻力增加，甚至失速，直接影响船舶的推进效率和操控性能。失速是翼型攻角增加到某个临界值时升力突然减小的一种状态，这是一种在船舶航行过程中不希望出现的现象[1]。因此如何有效抑制和延缓翼型结构的失速问题，在船舶工程中具有十分重要的工程价值和学术研究意义。

翼型表面流动分离是产生失速现象的本质原因之一，因此有效地抑制翼型表面的流动分离是抑制和延缓翼型失速现象的重要途径。目前对翼型结构表面流动分离的控制方法一般分为被动控制和主动控制两种。被动控制方法主要有采用柔壁型结构、安装端板、波浪形表面结构、尾刷、导流板和襟翼结构等方法[2-5]。由于被动控制方法属于预先设定的附加装置，当实际流动状态与设计状态不符时，难以达到预想的流动控制效果。主动控制方法主要有合成射流技术、吸吹气方法、等离子体技术以及电磁力控制，主动控制方法可根据流动状态调整控制参数，达到最佳的流动控制效果[6-10]。

海水作为天然的弱电解质给电磁力主动控制在船舶工程中的应用提供了先天的优势，而且电磁力控制具有响应速度快、无动作部件以及易操作等特点，因此电磁力控制方式在船舶工程中具有宽广的应用前景。Gailitis等[10]最早提出了电磁力主动控制方法，将相间分布的电极与磁极的激活板放置于弱电解质溶液，弱电解质中产生的Lorentz力作用改变了平板边界层的流动。上世纪末期，对此主动控制方法的研究逐渐开始趋向于机理和应用层面，研究者们开始研究电磁力对平板、道槽及圆柱绕流等流动的影响[11-14]。

近年来，利用电磁力控制翼型表面流动分离，进而延缓或抑制翼型失速现象的问题，成为国际上研究的热点。目前研究成果表明：电磁力作用增加了翼型近壁面流动速度，能够提高翼型最大失速攻角，在减阻方面也有较为显著的作用，电磁力作用可有效抑制和延缓翼型失速现象的发生，提高翼型的舵效。当电磁力作用与流动方向相反时，翼型上表面形成较显著的涡街结构[15-21]。在此基础上，研究者还对流向的洛伦兹力控制翼型绕流场的机理进行了深入的研究，且对洛伦兹力的控制效率的问题进行了讨论[22]。

由于受到实验条件的限制，目前的研究主要集中于翼型结构表面层流边界层分离时的电磁力控制问题，大多采用二维电磁力的近似公式对亚临界区低雷诺数时二维翼型结构的绕流场进行控制，对翼型结构失速后，电磁力控制绕流场中显著的三维特性和失速问题的控制规律和机理尚不十分清楚。

随着计算流体力学CFD技术的发展，数值模拟已成为研究电磁力流动主动控制的重要手段之一，其中针对高雷诺数的湍流问题主要采用RANS、LES和DES等方法[23]。RANS方法即雷诺平均方法，该方法模拟湍流脉动的平均流动作用，忽略了小尺度脉动信息，因此对复杂的非定常湍流模拟存在困难，对翼型结构附面层内大范围流动分离等现象的模拟结果并不十分精确。DNS方法即直接数值模拟方法，直接求解流场中的所有湍流尺度，但由于计算机能力的限制，目前还只能研究相对较低雷诺数的湍流流动问题。LES方法即大涡模拟方法，是一种介于RANS和DNS之间的湍流数值模拟方法，该方法也可以获得交警锡的真实瞬时流场，但在近壁面附近需要足够精细的网格，网格数量和质量要求较高，目前在实际工程中很难广泛应用。DES方法是一种介于LES和RANS之间的方法，综合了两者之间对流场数值模拟的优势，能够很好地处理高雷诺数时附面层内的大范围非稳态流动分离，不仅可以提高计算效率，还能获得比RANS方法更加精确的流动信息[24-25]。

有鉴于此，本文利用Maxwell方程直接数值分析表面包覆电极和磁极的翼型结构表面的三维电磁力，将其加入到流动控制方程中，在弦长雷诺数ReL=2.97×106时，采用DES数值模拟方法数值模拟电磁力作用下翼型失速攻角时绕流场特征，重点分析电磁力控制翼型失速后三维流场特性的规律及失速问题的机理。

1 数值模拟方法

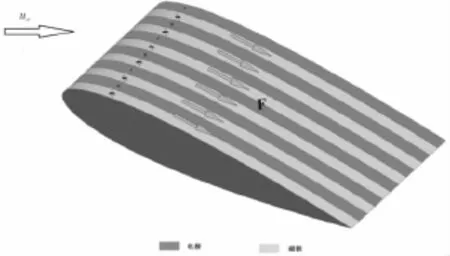
图1 表面覆盖电极与磁极翼型模型Fig.1 Configuration of the hydrofoil covered with electrodes and permanent magnets

在翼型上表面布置相间分布的电极和磁极，将其放置于弱电解质的海水中，对电极施加电压后，电极产生的电场与永磁体产生的磁场相互作用，在海水中形成流向的电磁力作用，如图1所示。其中：u∞为来流速度，F为电磁力。

将电磁力作为体积力加入到动量方程中，可得不可压缩流动Navier-Stokes方程为

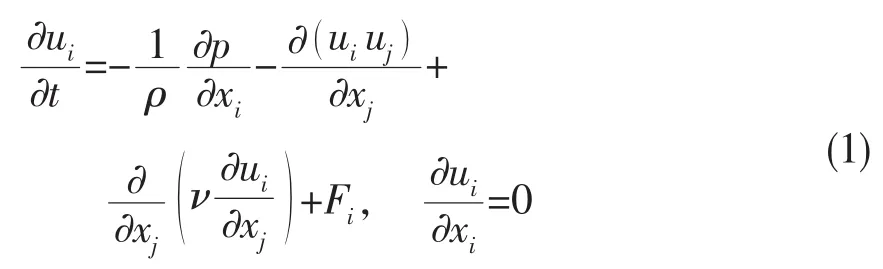
式中：t为时间；ρ为电解质密度；ν为运动黏度；u=（u1，u2，u3）为流场瞬时速度；p为扰动压力；F=（f1，f2，f3）为洛伦兹力；i，j为坐标轴方向。

流动的弱电解质在电磁场中受Lorentz力的作用，其表达式为

式中：J为电流密度，B为磁感应强度。电流密度J由两部分组成，一部分为电极产生的电流，另一部分为流体以速度u在磁场中运动产生的感应电流，可以表示为

式中：E为电场强度，σ为弱电解质电导率。在弱电解海水中，电导率σ很小，因此即便磁场强度很强，感应电流也很小，将Lorentz力表达式简化为

采用DES方法对流动控制方程进行数值模拟，DES方法主要思想是在近壁面处采用RANS方法模拟小尺度的脉动运动，而在远离壁面区域采用LES方法模拟大尺度脱体分离涡。在翼型壁面边界层内，将控制方程时间平均，采用基于SST k-ω湍流模型的RANS方法对边界层内流场进行数值模拟。在远离翼型壁面区域，将控制方程空间滤波，采用基于Smagorinsky亚格子模型的LES方法对附面层外的流场进行模拟[26]。

在SST k-ω湍流模型中k方程耗散项中的湍流尺度参数lk-ω的表达式为

式中：βk为模型常数，取值为βk=0.09。

在DES方法中，RANS和LES的分辨尺度lDES由下式定义：

其中，为了防止过早地开启亚格子应力模型引起附面层内雷诺应力的急剧下降，导致非物理性质的分离，产生网格诱导分离现象，系数CDES=0.61，Δ是网格尺度，对于非均匀网格有

在紧贴物面的区域，由于lk-ω≤CDESΔ，因此lDES=lk-ω，这时在DES中的湍流模型即为RANS中的SST k-ω湍流模型。在其它区域，由于lk-ω＞CDESΔ，因此SST k-ω湍流模型生成源项和消散源项中的lk-ω被替换为CDESΔ，当生成与消散作用达到平衡时，SST k-ω湍流模型中的湍动黏度与Smagorinsky模型中的亚格子涡黏系数在形式相似，这时DES方法与LES方法相似。

记yd为中截面上离开翼型壁面的垂向距离，电极磁极宽度a=0.01 m，由于流动分离主要发生在翼型的背压面，因此电极和磁极布置在翼型背压面上。利用Maxwell方程，采用有限元方法，对表面包覆电极与磁极的翼型表面的电磁力分布进行直接数值求解，结果如图2所示，其中（a）为法向电磁力密度为某展向断面处等势线分布。x为翼型弦向，y为翼型法向为电磁力。结果表明，电磁力在法向方向上呈指数衰减的现象，在翼型法向约0.015倍的弦长时已基本为零，沿展向呈周期性变化特性，最大值出现在电磁极交界处，其变化规律与文献[26]中圆柱表面的电磁力分布特征相类似。

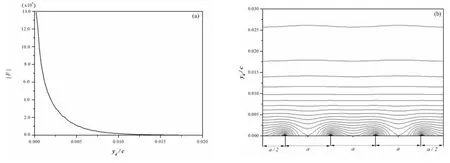
图2 翼型表面电磁力法向（a）和展向（b）分布的数值结果Fig.2 Three dimensional distribution of the Lorentz force around the hydrofoil (a)Normal direction(b)Spanwise direction

图3 计算区域平面示意图Fig.3 Schematic of a plane of the computational domain

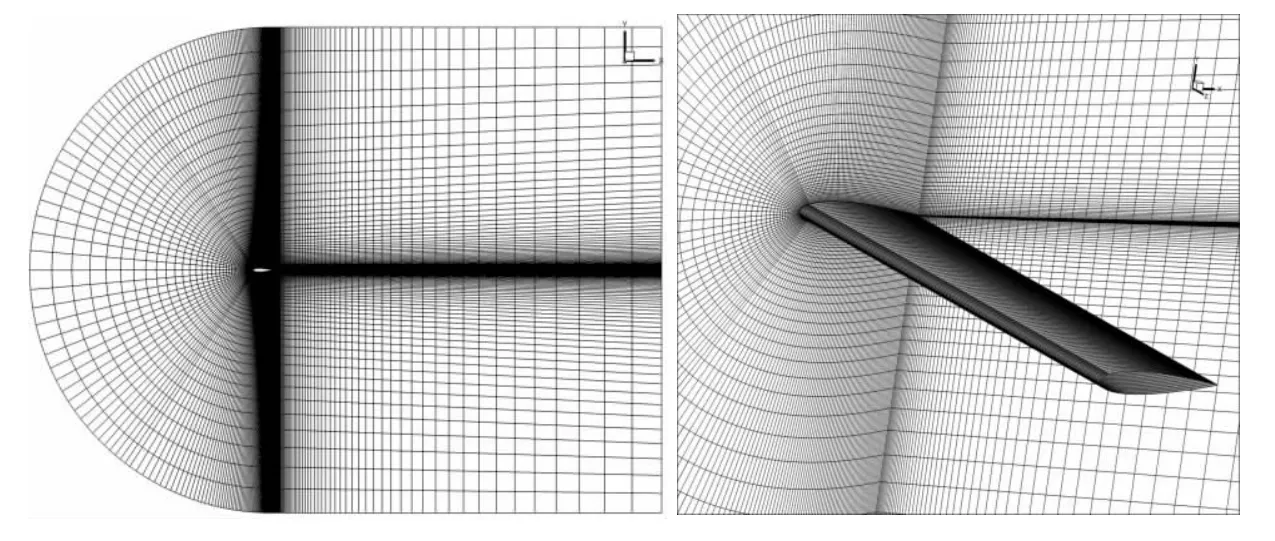
图4 数值计算平面及三维网格Fig.4 Mesh for numerical computations

本文针对NACA0018翼型进行研究，弦长c=0.3 m，攻角在5°～30°之间。数值模拟时，展向长度对翼型绕流场特性有明显的影响，因此为模拟翼型绕流场中完整的三维特性，翼型展向长度H选为5c。以翼型前缘起点为坐标原点，来流上游为12.5c，下游为21c，数值模拟计算平面区域如图3所示。入口边界为速度入口，出口边界为自由出流，上下边界为壁面边界条件，三维方向上为对称边界，翼型上下表面为无滑移壁面边界条件，以进口边界为计算初始条件。

数值模拟网格划分采用C型和H型网格对流场区域进行网格划分，翼型上下表面等分240份网格，展向在每个弦长高度等分30层网格，总网格为2.38×106。数值网格的平面及三维视图如图4所示。为了保证翼型壁面处第一层网格满足y+≈1，采用下式估算第一层网格控制点离开翼型壁面的距离Δy¯：

式中：弦长雷诺数ReL=u∞c/ν。采用有限体积法离散动量和连续性方程，对流项离散格式采用QUICK格式，扩散项采用中心差分格式，压力速度耦合迭代采用PISO算法，计算初始时间步长为Δt=0.001 s。

2 结果与分析

对翼型绕流场进行三维数值模拟时，定义翼型总阻力系数Cd、总升力系数Cl及电磁力作用参数N分别为

式中：Fd、Fl分别为翼型总阻力和升力，u∞为来流速度，S为浸湿面积；j0=σE0，E0为平均电场强度，B0为平均磁场强度。

2.1 无电磁力作用时数值结果

在数值模拟时弦长雷诺数ReL=2.97×106，弱电解质密度ρ=1 025 kg/m3，流体导电率为σ=5 s·m-1，运动黏度ν=10-6m2/s。首先对没有电磁力作用下翼型不同攻角时的绕流场特性进行数值模拟。当数值模拟时间t=20 s时，此时翼型绕流场已经达到稳定状态，然后再对不同攻角时的翼型绕流场施加电磁力作用，电磁力作用时间为5 s，计算结束时刻为t=25 s。

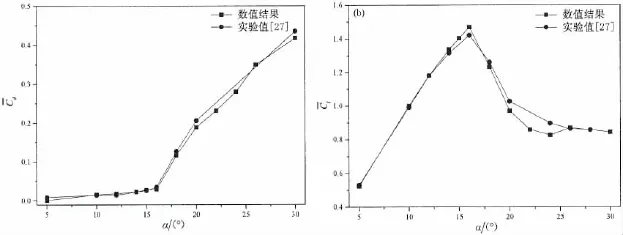
图5 当t=20 s时，翼型升阻力系数时均值数值与实验结果对比Fig.5 Comparisons of the time-average value of lift/drag coefficients results with the experimental values

结果表明：当翼型攻角小于失速攻角时，升力系数随着攻角的增加而增大，阻力系数缓慢增大，当攻角大于失速攻角时，升力系数急剧减小，阻力系数急剧增加。由此可知：翼型失速时，其升力减小，阻力增加，在实际应用中是不期望出现的一种现象，因为这会导致翼型效率降低，甚至不能够产生足够的有效升力，直接影响其稳定性和操控性能。

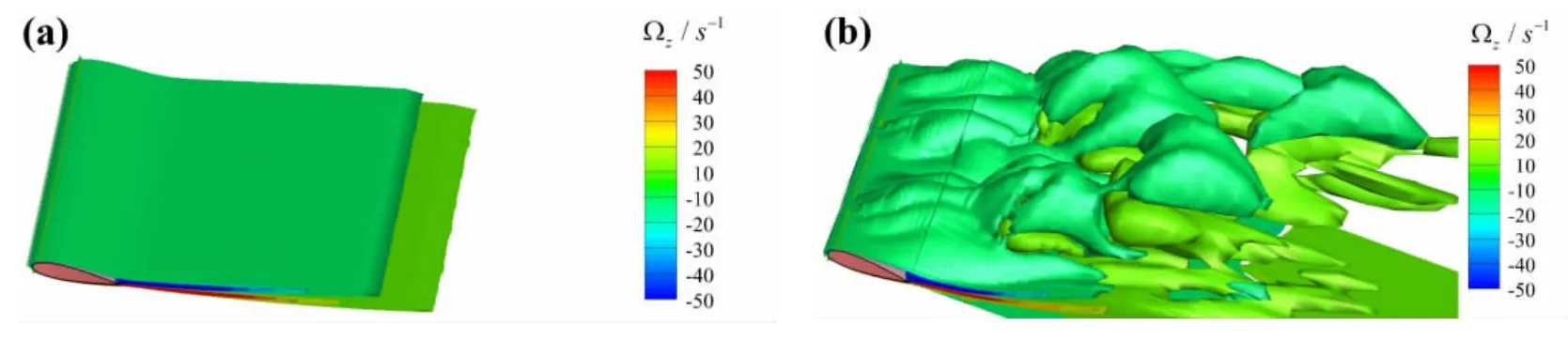
图6 当t=20 s时，翼型失速前后绕流场涡量场分布 （a）α=12°；（b）α=20°Fig.6 Numerical results for the vorticity distribution at different attack angles(a)α=12°;(b)α=20°

图6中给出了翼型失速前和失速后两个不同攻角时涡量场数值结果，图中Ωz为展向涡量。图中结果表明，当攻角α=12°时，流体流过翼型时，在翼型背压面后缘产生小尺度流动分离现象，仅在翼型上下表面的尾缘处有狭长的涡量场分布，此时翼型绕流场中的涡量场特性显现为典型层流分离中长泡分离现象[28]，涡量场分布具有层流流动特性。当攻角α=20°时，流体流经翼型时，流体在翼型上表面产生大尺度流动分离，流场中有明显的漩涡产生，翼型绕流场中具有显著的三维特性。翼型失速后大尺度流动分离增加了翼型前后的压差阻力，升力急剧减小，阻力增加。

2.2 电磁力作用对翼型流场特性的影响

首先考虑电磁力作用对翼型绕流场流动特性的影响规律。当攻角一定时，随着电磁力作用参数的改变，翼型绕流场特性随之改变。图7和图8分别给出了ReL=2.97×106下翼型失速后，当α=20°时电磁力作用下流场中三维涡量场及不同展向断面处涡量变化特性。

图中结果表明，电磁力作用可以抑制涡量场展向大尺度脉动，随着电磁力作用的增加，电磁力可抑制翼型表面的流动分离，当电磁力作用足够大时，翼型绕流场中涡量场首先转变为层流分离泡模型中长泡分离状态，随电磁力作用再增加，在翼型后方电磁力作用推动翼型表面的流体流动，产生类似射流状狭长涡结构。具体变化规律如下：

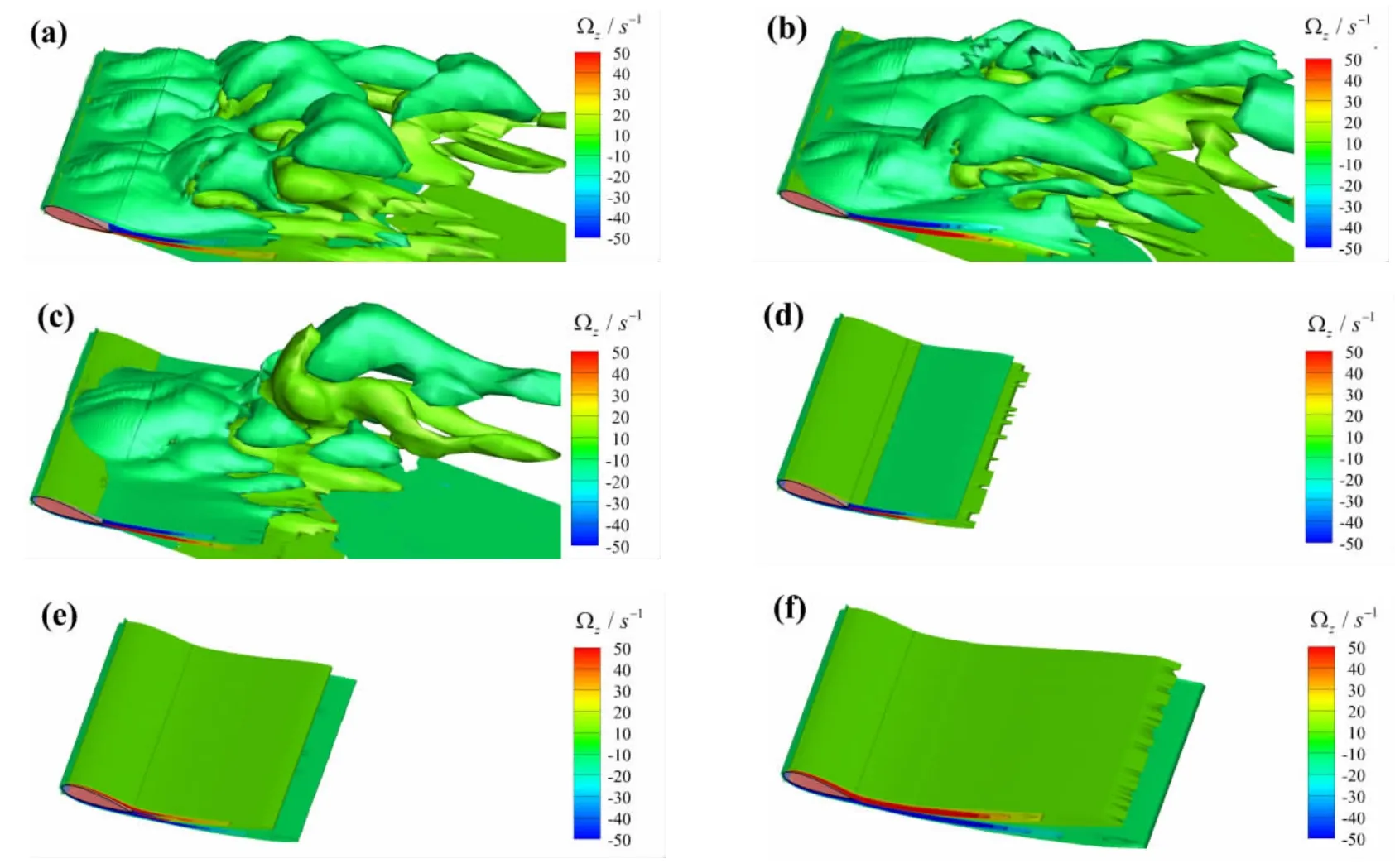
图7 当α=20°和t=25 s时，电磁力作用下翼型绕流场中涡量场数值结果（a）N=0；（b）N=0.1；（c）N=0.25；（d）N=0.5；（e）N=1；（f）N=2Fig.7 Numerical results for the vorticity distribution due to the electromagnetic force when t=25 s and α=20° (a)N=0;(b)N=0.1;(c)N=0.25;(d)N=0.5;(e)N=1;(f)N=2

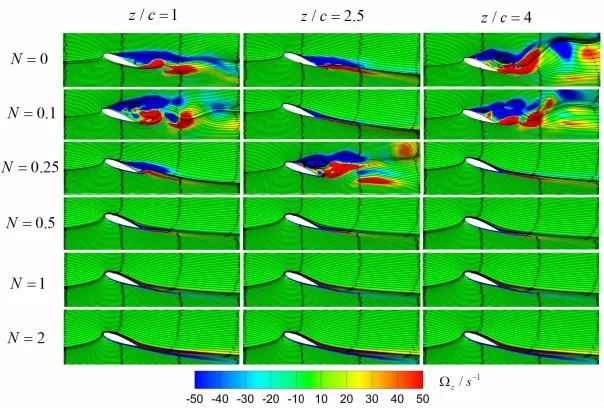
图8 当α=20°和t=25 s时，翼型不同展向断面处涡量场数值结果Fig.8 Numerical results for the vorticity distribution of different spanwise sections due to the electromagnetic force when t=25 s and α=20°

当N=0，即没有电磁力作用时，翼型后方产生具有显著三维特性的大尺度涡街结构，展向不同断面处涡量分布有明显区别，不同断面处流动分离的位置亦具有显著差异。当N=0.1时，此时电磁力作用较小，电磁力作用仅改变了翼型前缘处的流动状态，不同展向断面处涡量分布依旧具有显著的差异，尾流场中涡街结构的变化并不明显。当N=0.25时，电磁力作用增加，在翼型展向方向上，大尺度涡街结构有所减少，由于展向不同断面处涡量分布的相位并不相同，在翼型展向中截面附近区域依旧存在大尺度涡结构。当N=0.5时，电磁力作用将翼型表面流动分离完全抑制，不同展向断面处涡量场分布特征逐渐一致，流动状态类似于翼型未失速时典型层流分离中长泡分离特征，翼型上表面涡量逐渐增加，开始出现正向的涡量。当N=1时，翼型上表面涡量由负涡量转变为正涡量，此时翼型表面速度场特征发生明显变化，在翼型尾部涡量场中出现正负涡量交叉分布特征，涡量场分布不再由流动分离而导致，而是由电磁力推动了翼型表面流动加速形成狭长状涡结构。随电磁力作用再增加，当N=2时，翼型上表面涡量全部转变为正涡量，由电磁力作用产生的涡结构影响范围逐渐增加，并向流动方向的下游发展。

图9中给出了ReL=2.97×106，α=20°时，翼型展向z/c=2.5中截面处上表面速度u随yd的变化，其中x/c=0和x/c=1.0分别为翼型的前缘和后缘。结果可知：当没有电磁力作用时，在翼型展向中截面处翼型前缘速度最大，随着向翼型后缘移动，速度值逐渐减小，而且出现速度方向上的变化，由此可知在翼型上表面具有较明显的速度梯度变化，当N=0.1和N=0.25时，此时电磁力作用较小，由流场结果可知翼型绕流场中存在显著的三维特性，此时展向不同断面处分离涡脱落的相位存在差异，在展向中截面处的速度场分布并没有明显的规律性，但当yd＞0.6c时，不同断面处的速度基本一致。当N=0.5时，翼型上表面各处速度显著增加，随着yd的增加，流体速度首先增加然后再逐渐与外流场速度相一致，从翼型前缘到后缘不同垂向断面处上表面的速度逐渐减小，当x/c=0.8断面时，边界层内的速度与外流场几乎相当。当N=1时，翼型上表面各处的速度值继续增大，当在断面x/c=1.0时，即在翼型后缘处，其边界层内的速度大小与外流场速度基本达到一致，当yd大于电磁力作用范围时，其速度值又有所减小，因此电磁力作用使得翼型上表面接近尾缘处的速度梯度方向发生改变，导致电磁力作用范围内的涡量场由负涡量转变为正涡量。N=2时，壁面边界层内的速度明显增大且超过外流场的速度值，因此当yd大于电磁力作用的影响范围时，其速度场又明显减小，此时电磁力作用使上表面正向涡量更加显著，在流向x方向上的影响范围亦增加。

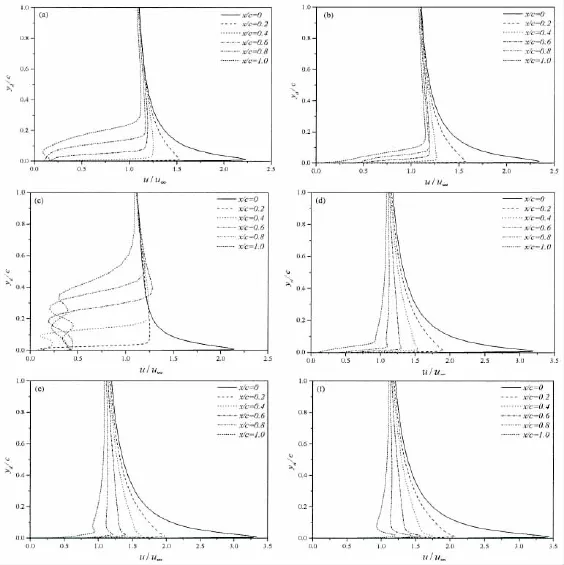
图9 当α=20°和t=25 s时，翼型展向中截面上表面速度u随yd变化的数值结果（a）N=0；（b）N=0.1；（c）N=0.25；（d）N=0.5；（e）N=1；（f）N=2Fig.9 Effect of the electromagnetic force on the tangential velocity near the up-surface of hydrofoil at the middle spanwise section when t=25 s and α=20°(a)N=0;(b)N=0.1;(c)N=0.25;(d)N=0.5;(e)N=1;(f)N=2

2.3 电磁力作用对翼型失速特性的影响

图10中给出了当攻角α=20°时，不同电磁力作用下，升力系数时历及时均值的数值结果。由图10（a）升力系数时历数值结果可知，在无电磁力作用时，由于翼型绕流场中存在显著的大尺度分离涡结构，其升力系数时历没有明显周期性特征，存在有较大的随机性。当施加电磁力作用时，随着电磁力作用的增加，升力系数随之增加，且其随机脉动幅值逐渐减小。当N=0.5时，已不存在明显的脉动量，这说明此时翼型绕流场中已没有三维特性存在，翼型表面不存在大尺度的流动分离现象。由图10（b）升力系数时均值的结果可知：当N≤0.5时，升力系数时均值随着电磁力作用的增加近似线性增加，当N＞0.5时，升力系数时均值随电磁力作用增加亦近似线性增加，但增加速率有所减缓。

图10 当α=20°时，电磁力作用对总升力系数Cl时历及其时均值的影响 （a）Cl；（b）Fig.10 Effect of the electromagnetic force on the time history and the time average value of the lift coefficients at α=20°(a)Cl;(b)

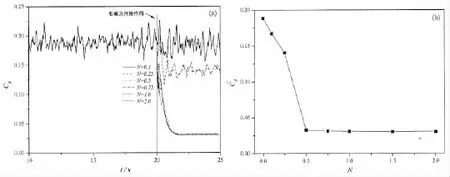
图11 当α=20°时，电磁力作用对总阻力系数Cd时历及其时均值的影响 （a）Cd；（b）Fig.11 Effect of the electromagnetic force on the time history and the time average value of the drag coefficients at α=20°(a)Cd;(b)

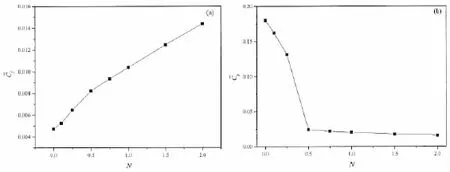
图12 当α=20°时，电磁力作用对摩擦阻力系数时均值和压差阻力系数时均值的影响 （a）；（b）Fig.12 Effect of the electromagnetic force on the total average pressure and friction coefficients at α=20°(a);(b)

图11中给出了当攻角α=20°时，不同电磁力作用下阻力系数时历及其时均值的数值结果。由图11（a）阻力系数时历结果可知：当N=0.1时，电磁力作用较小，阻力系数的时历变化并不明显，随着电磁力作用的增加阻力系数减小，其脉动幅值也显著减小。当电磁力作用N＞0.5时，电磁力作用稳定后，其阻力系数变化并不明显。由图11（b）中的时均值的结果可知：当N≤0.5时，阻力系数时均值随电磁力作用参数的增加总体上呈现近似线性显著减小；当N＞0.5时，阻力系数的变化趋于平缓，此时阻力系数大小基本与翼型未失速时阻力系数大小相当。

图12中给出了当攻角α=20°时，电磁力作用对摩擦阻力系数和压差阻力系数时均值的影响。图12（a）中摩擦阻力系数时均值数值结果可知：摩擦阻力系数随电磁力作用的增加在N≤0.5和N＞0.5时均呈现线性增加的趋势，且当N＞0.5时，摩擦阻力系数增加的速率要比N≤0.5时要小。图12（b）为压差阻力系数时均值的结果表明：当N≤0.5时，其变化特征与总阻力系数时均值变化特征相类似；当N＞0.5时，压差阻力系数随电磁力作用的增加近似线性减小，但减小的速率与摩擦阻力系数增加的速率相差不大，因此造成了图11（b）中阻力系数变化并不明显的现象。

升阻比是衡量翼型工作性能的重要标志，图13中给出了当攻角α=20°时，电磁力作用对翼型升阻比的影响特性。结果可知：翼型升阻比随着电磁力作用的增加而增大，当N≤0.25，电磁力作用较小时，升阻比略有增加但并不显著；但N=0.5时，翼型升阻比突然增大，随着电磁力作用再增加，升阻比增加的速率逐渐平缓。

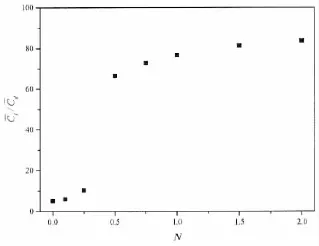
图13 当α=20°时，电磁力作用升阻比的影响特性Fig.13 Effect of the electromagnetic force on the lift-drag ratio at α=20°

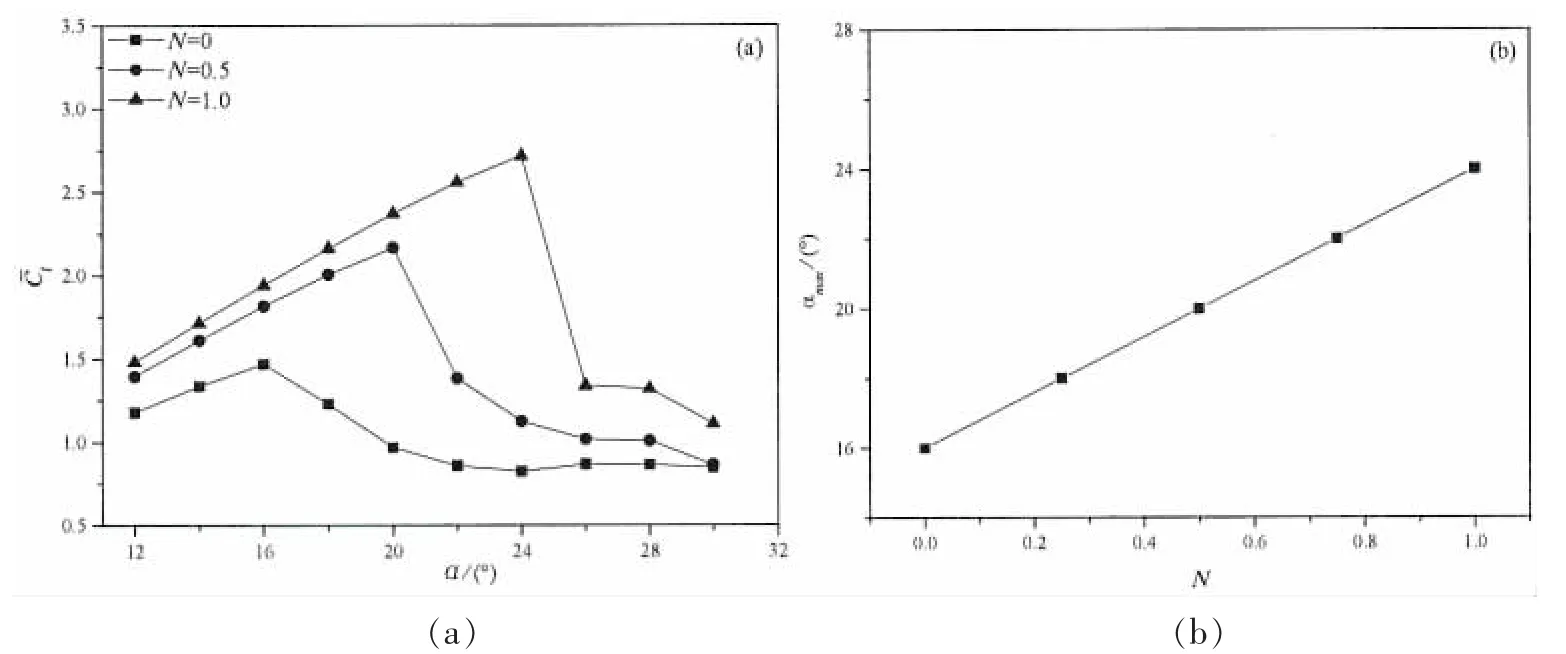
图14 电磁力作用下对升力系数时均值及最大升力角的影响Fig.14 Effect of the electromagnetic force on the time-averaged value of the lift coefficients and the angles of maximum lift

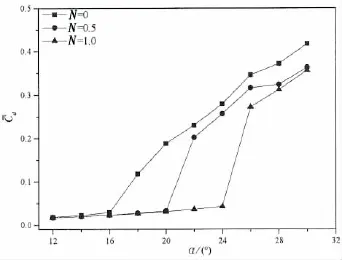
图15 电磁力作用对阻力系数时均值的影响Fig.15 Effect of the electromagnetic force on the time-averaged of the drag coefficients

为研究电磁力作用对翼型失速特性的影响，图14分别给出了电磁力作用对翼型升力系数时均值及失速攻角的影响。图14（a）升力系数时均值的结果表明：随着电磁力作用的增加，翼型升力系数时均值增大，电磁力作用下，翼型依旧产生失速现象，翼型失速后，其升力依然急剧减小，但相对于未受电磁力控制时依旧增加。图14（b）中最大失速攻角随电磁力作用的变化结果，结果显示在给出的电磁力作用范围内，最大失速攻角随着电磁力作用的增加近似线性增加。

图15给出了电磁力作用对阻力系数时均值的影响。结果表明：电磁力作用下，阻力系数时均值突然增加的攻角显著提高，即翼型发生失速时的攻角增加，当翼型失速后，随着攻角的增加，阻力系数时均值急剧增加，翼型发生失速现象。

3 结 论

利用Maxwell方程直接数值计算表面包覆电极与磁极翼型产生的三维电磁力分布，将其加入到流体控制方程的动量方程中，在弦长雷诺数ReL=2.97×106时，采用脱体涡模拟方法对弱电解质中电磁力作用下翼型绕流场的流场特性进行了数值模拟，研究了电磁力作用控制失速攻角α=20°时，翼型绕流场中显著的三维特性的规律和失速问题机理。

结果表明：当电磁力作用参数N＜0.25时，电磁力作用对翼型绕流场的控制效果并不显著；当N= 0.5时，电磁力作用可以抑制翼型表面的大尺度流动分离，将翼型绕流场转变为未失速时的层流分离状态；当N＞0.5时，翼型表面流动速度显著增加，速度梯度方向发生转变，表面涡量显著增加，涡量由负涡量转变为正涡量，翼型后方狭长涡由电磁力作用产生，随电磁力作用的增加，电磁力作用产生的狭长涡向下游影响范围增加。

当电磁力作用参数N＜0.5时，电磁力作用显著减小翼型升阻力系数的脉动幅值，使得翼型升力系数增加，阻力系数减小，升阻比增加，但升阻比增加速率较缓慢；当N=0.5时，翼型升力和阻力系数的脉动幅值基本减小到零，翼型升阻比显著增大；当N＞0.5时，翼型升阻比增加的速率逐渐减缓。电磁力作用可有效延缓翼型失速问题，提高翼型工作性能。

[1]Ekaterinaris John A,Platzer Max F.Computational prediction of airfoil dynamic stall[J].Aerospace Sci,1997,33:759-846.

[2]马 侠,肖林奎,蒋金贵等.用NS方程求解柔壁翼型绕流[J].航空动力学报,1993,8(1):11-18. Ma Xia,Xiao Linkui,Jiang Jingui,et al.Computation of flexible-wall airfoil flow using N-S equations[J].Journal of Aerospace Power,1993,8(1):11-18.

[3]Tang D,Dowell E H.Aerodyamic flow control of an airfoil with small trailing-edge strips[J].Journal of Aircraft,2006,43 (6):1854-1866.

[4]郝礼书,乔志德,宋文萍.基于涡流发生器和Gurney襟翼的翼型绕流流动控制试验研究[J].航空学报,2011,32(8): 1429-1434. Hao Lishu,Qiao Zhide,Song Wenping.Experimental research on control flow over airfoil based on vortex generator and gurney flap[J].Acta Aeronautica ET Astrnautica Sinica,2011,32(8):1429-1434.

[5]Staelens Y D,Blackwelder R F,Page M A.Novel pitch control effectors for a blended wing body airplane in takeoff and landing configuration[J].AIAA Paper,2007:68-229.

[6]Hao Feng L,Wang J J,Pan C.Effect of novel synthetic jet on wake vortex shedding modes of a circular cylinder[J].Journal of Fluids and Structures,2010,26(6):900-917.

[7]Corke T C,Enloe C L,Wilkinson S P.Dielectric barrier discharge plasma actuators for flow control[J].Annual Review of Fluid Mechanics,2010,42:505-529.

[8]Li Z,Navon I M,Hussaini M Y,et al.Optimal control of cylinder wakes via suction and blowing[J].Computers&Fluids, 2003,32(2):149-171.

[9]Henoch C,Stace J.Experimental investigation of a salt water turbulent boundary layer modified by an applied streamwise magnetohydrodynamic body force[J].Phys Fluids,1995,7(6):1371-1383.

[10]Gailitis A,Lielausis O.On a possibility to reduce the hydrodynamic resistance of a plate in a electrolyte[C].Applied Magneto hydrodynamics Report of the Physics Institute Riga 12,1961:143-146.

[11]Mutschke G,Gerbeth G,Shatrov V,et al.Two-and three-dimensional instabilities of the cylinder wake in an aligned magnetic field[J].Physics of Fluids,1997,9:3114.

[12]Weier T,Fey U,Gerbeth G,et al.Boundary layer control by means of wall parallel Lorentz forces[J].Magnetohydrodynamics,2001,37(1/2):177-186.

[13]梅栋杰,范宝春,黄乐萍等.槽道湍流的展向振荡电磁力壁面减阻[J].物理学报,2010,59(10):6786-6792. Mei Dongjie,Fan Baochun,Huang Leping,et al.Drag reduction in turbulent channel flow by spanwise oscillating Lorentz force[J].Acta Phys.Sin,2010,59(10):6786-6792.

[14]Zhang H,Fan B C,Chen Z H.In-depth study on cylinder wake controlled by Lorentz force[J].Chinese Physics Letters, 2011,28(12):124701.

[15]Weier T,Gerbeth G.Control of separated flows by time periodic Lorentz forces[J].European Journal of Mechanics B/Fluids,2004,23:835-849.

[16]Cierpka C,Weier T,Gerbeth G.Synchronized force and particle image velocimetry measurements on a NACA 0015 in poststall under control of time periodic electromagnetic forcing[J].Phys.Fluids,2010,22(7):075109.

[17]陈耀慧,范宝春,陈志华等.翼型绕流电磁控制的实验和数值研究[J].物理学报,2008,57(2):648-653. Chen Yaohui,Fan Baochun,Chen Zhihua,et al.Experimental and numerical investigations on the electro-magnetic control of hydrofoil wake[J].Acta Phys.Sin,2008,57(2):648-653.

[18]Chen Y H,Fan B C,Chen Z H,et al.Influences of Lorentz force on the hydrofoil lift[J].Acta Mechanica Sinica,2009, 25(5):589-595.

[19]刘宗凯,周本谋,刘会星等.电磁流体表面推进机理与效果分析[J].物理学报,2011,60(8):84701. Liu Zongkai,Zhou Benmou,Liu Huixing,et al.The analysis of effects and theories for electromagnetic hydrodynamics propulsion by surface[J].Acta Phys.Sin,2011,60(8):84701.

[20]Albrecht T,Weier T,Gerbeth G,et al.Numerical and experimental investigation of electromagnetic separation control using different wave forms[C]//5th AIAA Flow Control Conference.Chicaco,IL,USA,.2010.

[21]Mutschke G,Gerbeth G,Albrecht T,el al.Separation control at hydrofoil using Lorentz forces[J].European Journal of Mechanics-B/Fluids,2006,25(2):137-152.

[22]陈耀慧,董祥瑞,陈志华等.翼型绕流的洛伦兹力控制机理[J].物理学报,2014,63(3):034701. Chen Yaohui,Dong Xiangrui,Chen Zhihua,et al.Control of flow around hydrofoil using the Lorentz force[J].Acta Phys. Sin,2014,63(3):034701.

[23]Breuer M,Jovicˇic＇N,Mazaev K.Comparison of DES,RANS and LES for the separated flow around a flat plate at high incidence[J].International Journal for Numerical Methods in Fluids,2003,41(4):357-388.

[24]STRELETS M.Detached eddy simulation of massively separated flows[R].AIAA,USA,2001:0879.

[25]Dong L,Men’shov I,Nakamura Y.Numerical prediction for airfoil Stall[J].ICAS2004,Yokohama,Japan,2004.

[26]尹纪富,尤云祥,李 巍等.电磁力控制湍流边界层分离圆柱绕流场特性数值分析[J].物理学报,2014,63(4): 044701. Yin Jifu,You Yunxiang,Li Wei,et al.Numerical analysis for the characteristics of flow control around a circular cylinder with a turbulent b oundary layer separation using the electromagnetic force[J].Acta Phys.Sin,2014,63(4):044701.

[27]Jacobs E N,Sherman A.Airfoil section characteristics as affected by variations of the Reynolds number[M].National Advisory Committee for Aeronautics,1937.

[28]Horton H P.Laminar separation bubbles in two-and three-dimensional incompressible flow[D].PhDThesis.London:University of London,1968.

Numerical investigation on the three-dimensional flow characteristics around a hydrofoil influenced by the electromagnetic force

YIN Ji-fu1,2,LIN Zhong-yi3,LI Wei1,YOU Yun-xiang1,HU Tian-qun1
(1.State Key Laboratory of Ocean Engineering,Shanghai Jiao Tong University,Shanghai 200240,China;2.CCCC National Engineer Research Center of Dredging Technology and Equipment,Shanghai 201208,China;3.School of Jiaxing Nanyang Profession and Technology,Jiaxing 314003,China)

This paper numerically researches the flow structures around a hydrofoil and the lift/drag characteristics influenced by the electromagnetic force in a weakly conductive fluid at a chord length Reynolds number2.9×106with the method of detached eddy simulation(DES).The effects of the electromagnetic force on the three-dimensional flow characteristics and stall problem of a hydrofoil are investigated at a stall attack angle α=20°.The results show that the electromagnetic force can improve the flow structures around a hydrofoil and significantly reduce the three-dimensional flow characteristics.The electromagnetic force increases the kinetic energy near the boundary layer of the hydrofoil surface,delay the flow separation and change the vorticity field characteristics.Meanwhile,the electromagnetic force can decrease the drag force and the fluctuation amplitudes of the lift,increase the lift,reduce the drag,and raise the lift-drag ratio. Moreover,the electromagnetic force can significantly delay the stall problem and increase the stall angle, improve the working performance.

electromagnetic force;flow around a hydrofoil;stall;numerical simulation

O361

A

10.3969/j.issn.1007-7294.2016.07.005

1007-7294（2016）11-1388-12

2016-09-22

国家自然科学基金（11272211）；上海交通大学海洋工程国家重点实验室研究基金资助课题（GP010819）

尹纪富（1984-），男，博士研究生，E-mail：yinjifuytu@163.com；尤云祥（1963-），男，教授，博士生导师，通讯作者，E-mail：youyx@sjtu.edu.cn。