2016 年高考数学全国卷试题评析与新一轮高考数学复习建议(上)

◇ 北京 丁益祥(特级教师)

(作者单位：北京陈经纶中学)



2016 年高考数学全国卷试题评析与新一轮高考数学复习建议(上)

◇ 北京 丁益祥(特级教师)

1 试题总体评价

2016年全国高考数学甲、乙、丙3套试题,都依照考试大纲的要求,较好地坚持了“考查基础知识的同时,注重考查能力”的原则.在以能力立意的命题思想指导下,着意将知识、能力与素质融为一体,全面检测了考生的数学素养.

试题注意了数学的学科特点,突出了知识的基础性和综合性,以主干知识为主体,注意在知识网络交会点设计试题.着力体现概念性、思辨性和应用性,在数学思想、理性思维以及数学潜能方面都作了比较深入的考查.试题总体难度适中,除了个别把关试题较难外,大部分试题平和稳定、似曾相识、稳中有变、推陈出新.既考查了中学数学的知识和方法,又检测了考生进入高校继续学习的潜能,发挥了数学作为基础学科应有的作用.

2 主要特点分析

2.1 在考查双基中凸显重点内容

2016年的数学《考试大纲》在考查要求中明确指出:“对数学基础知识的考查,既要全面又要突出重点,对于支撑学科知识体系的重点内容,要占有较大的比例,构成数学试题的主体.”

《考试大纲》的这一命题要求,在2016年全国甲、乙、丙3套数学试题中都得到了较好的落实.试题一方面对高中数学所涉及的概念、性质、公式、法则、定理、公理等都作了较为全面的考查,知识点覆盖面约占所有知识点的65%;另一方面凸显了对导数与函数、三角函数(包括三角恒等变换和解三角形)、平面向量与空间向量、数列、不等式、概率与统计、圆锥曲线与方程、空间图形与平面图形等8个重要部分内容的考查.

我们以2016年全国甲、乙、丙3套理科试题作说明见表1.这些都充分说明在全面考查双基的同时,凸显重点内容重点考查、重点内容反复考查的命题特点.

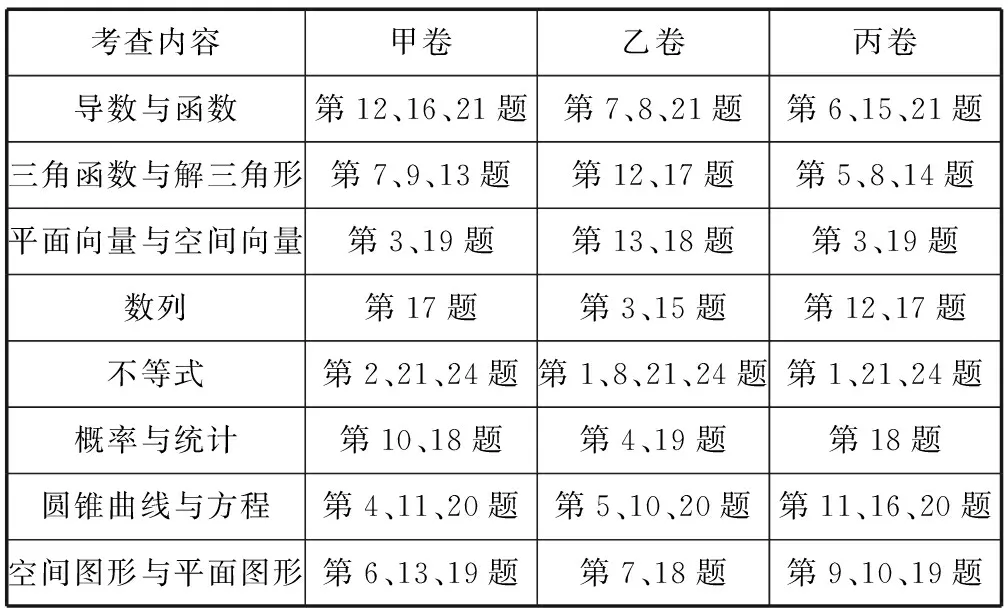
表1

2.2 在考查交会中提高学科能力

2016年甲、乙、丙3套数学试题,都十分重视从学科的整体高度和思维价值的高度,凸显对知识网络交会问题的考查,据此检测学生的数学能力.

(1) 证明|EA|+|EB|为定值,并写出点E的轨迹方程;

(2) 设点E的轨迹为曲线C1,直线l交C1于M、N2点,过B且与l垂直的直线与圆A交于P、Q2点,求四边形MPNQ面积的取值范围.

分析与评述 此题第(1)问是2条线段长度之和的定值问题和动点的轨迹问题,充分利用平面几何中圆的性质、等腰三角形的性质以及平行线的性质,不难证明|EA|+|EB|等于已知定圆的半径,当然是定值.再结合椭圆的定义,即可判断动点E的轨迹是椭圆,进而可写出其方程.

解决第(2)问的前提是求出四边形MPNQ的面积函数,然后确定其取值范围.注意到这个四边形的4个顶点是由直线l与第(1)问中求出的椭圆C1的交点,以及过点B且垂直于l的直线与已知圆的交点所确定的,这自然想到应考虑直线l斜率的存在与否,所以应分“直线l与x轴不垂直”和“直线l与x轴垂直”2种情况讨论.此外,无论是上述哪一种情况,都可以把四边形分割成2个三角形来处理.为此需要通过弦长公式或圆的半径、弦心距以及半弦所构成的直角三角形,利用勾股定理求弦长,然后根据上述2种情况再确定四边形面积的取值范围.

显然,此题突出了解析几何与平面几何的交会,具有较强的综合性,着重考查了直线与圆及椭圆的位置关系、椭圆的定义、弦长公式、平行线的性质、勾股定理、三角形面积等知识,考查了分类与整合的思想以及运算求解能力和推理论证能力.通过此类问题求解,可以有效地检测和提高学生的数学能力.

2.3 在考查应用中强化应用意识

数学应用问题的考查由来已久,2016年应用问题在保持考查概率与统计模型的基础上,又关注了其他数学模型应用问题的考查.

图1

(1) 求X的分布列;

(2) 若要求P(X≤n)≥0.5,确定n的最小值;

(3) 以购买易损零件所需费用的期望值为决策依据,在n=19与n=20之中选其一,应选用哪个?

分析与评述 第(1)问给出了关于100台这种机器在3年使用期内更换的易损零件数的柱状图,并且在“以这100台机器更换的易损零件数的频率代替1台机器更换的易损零件数发生的概率”的条件下,求2台机器3年内共需更换的易损零件数X的分布列.核心是X可取值的确定及相应概率的分析和计算.

第(2)问是在第(1)问基础上的自然引申.事实上,只需根据第(1)问所求出的X的分布列,通过计算、比较,便可以确定n的最小值.

处理第(3)问,首先应弄清购买零件的费用所包括的2个方面:1)购买机器时同时购买的零件所需费用,按每个200元计算; 2)备用零件不足时另外购买的零件,按每个500元计算.在此基础上,分别计算n=19与n=20这2种情况下各自所需费用的分布列,进而求出期望,再比较大小,即可作出正确决策.

不难看出,此题着重考查离散型随机变量的分布列和期望.后2问从经济核算的角度,考查了在数理统计基础上的理性决策,体现了概率统计知识在实际问题中的应用.这种概率统计知识的命题方式,既是近几年高考试题的热点,又是亮点,具有浓郁的应用味儿,它有效地检测了学生的应用意识和实践能力.

图2

A 各月的平均最低气温都在0℃以上;

B 7月的平均温差比1月的平均温差大;

C 3月和11月的平均最高气温基本相同;

D 平均气温高于20℃的月份有5个

分析与评述 由雷达图可看出:对于选项A,0℃在虚线为边界的图形内,故各月的平均最低气温都在0℃以上,因此A正确.对于选项B,7月的平均温差大于7.5℃,1月的平均温差小于7.5℃,所以7月的平均温差比1月的平均温差大,因此B正确.对于选项C,3月和11月的平均最高气温大约都在10℃左右,所以3月和11月的平均最高气温基本相同,因此C正确.由此可知D错误,因此选D.

事实上,由雷达图可看出,平均气温高于20℃的只有3个月份(6、7、8月),因此D错误.

此题是关于某城市气温情况的实际问题.问题的解决利用了雷达图的阅读和分析技术,这种技术是基于一种形似导航雷达显示屏上的图形而构建的一种多变量对比分析技术,雷达图是统计图中的一种,它由若干个同心圆以及从圆心向外引出的若干条射线构成.这些同心圆的间距相等,每个圆代表一定的指标值.解题时,通常将同一类变量不同时期的指标值依次连接成封闭折线,从而获得不同类别变量不同的折线图,再进行对比分析,进而作出相应的判断.

这里,雷达图只是这个旅游城市用来向游客介绍本地气温情况的一种形式.命制此题的弦外之音是数学应用意识的考查,除了概率与统计问题以外,还有涉及其他知识的问题.此题的考查为我们把握应用问题的复习内容和方向,提供了新的视角.同时,通过不同知识内容实际问题的考查,体现数学应用的广泛性,以此不断强化学生的数学应用意识.

(未完待续)

(作者单位：北京陈经纶中学)