斜拉桥π型梁桥面板剪力滞效应的优化计算方法

赵傲，苗林，陈德伟

（同济大学 土木工程学院，上海 200092）

斜拉桥π型梁桥面板剪力滞效应的优化计算方法

赵傲，苗林，陈德伟

（同济大学 土木工程学院，上海 200092）

用能量变分法分析剪力滞作用时，一般认为截面腹板部分符合初等梁理论的平截面假定，截面的中性轴过形心轴，这种假定在箱型梁中基本适用，然而在π型梁超宽桥面板中，由于剪力滞的影响，桥面板被大大削弱，截面中性轴相对形心轴有较大偏移，在理论分析中无法忽略。文章考虑π型梁截面中性轴偏移，通过对辰塔大桥π型梁悬臂施工过程进行有限元模拟，解析解与数值解吻合良好，证实了该文的分析方法和假设是正确的，对T型梁及π型梁剪力滞效应研究提供参考。

混凝土斜拉桥；剪力滞效应；能量变分法

1 概述

桥梁结构中，主梁在对称荷载作用下法向应力沿横截面的分布是不均匀的，这种现象称为剪力滞效应。用能量变分法分析剪力滞效应时，通过平截面假定和中性层假定，我们可以非常方便地表达截面上各点的应力应变，通常认为中性层恰好通过截面形心，然而，由于剪力滞效应对桥面板存在一定“削弱”作用，使得中性层与形心存在一定偏差，在箱型截面中，由于顶底板均存在剪力滞效应，这种偏差并不明显，可以忽略；但是在开口截面如T型梁和π型梁中，桥面板中剪力滞效应引起的这种偏差无法忽略，在理论分析中必须加以考虑。

本文以上海辰塔大桥混凝土π型梁为对象，考虑中性轴偏移，运用能量变分法求解截面应力分布，同时利用Ansys进行有限元模拟，通过数值案例验证本文所述分析方法的正确性。

2 计算基本假定

2.1 E.Reissner函数的确定

如图1，斜拉桥主梁可看作受均布荷载与集中荷载共同作用而发生竖向挠曲变形的悬臂梁，若选取剪力滞效应引起的附加挠度作为剪力滞广义位移，ψ（x）采用E.Reissner函数R（y）描述翼板纵桥向x方向位移在横桥向y方向的分布[1]，定义梁的纵向整体位移u（x）及竖向挠度ω（x），截面上顶板及腹板的纵向位移可分别表示为：

图1 π型梁截面及受力示意图

应用能量变分方法分析时，采用E.Reissner函数描述翼板纵桥向（x方向）位移沿横桥向（y方向）的分布曲线，假定为抛物线分布，符合实测结果[2]。由薄壁梁截面局部平衡条件得到多项式函数表达式[3]：

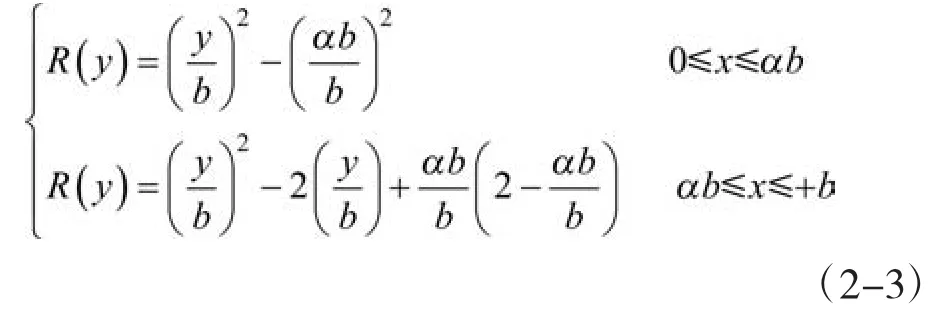
式中：b为翼板y方向净宽的1/2；ab为主肋内侧y方向距离的一半。

2.2 中性轴与形心轴偏移量

在梁的弯曲正应力分析过程中，存在两个重要假设：平截面假定和中性层假设，通过这两个假设，可以非常方便地表达截面内部应变，中性层与横截面的交线即为中性轴，中性轴与形心轴重合[4]。

而在斜拉桥施工过程中，π型超宽桥面板在弯矩及斜拉索轴向分力作用下存在较为明显的剪力滞效应，对桥面板起到一定的“削弱”作用，截面的中性轴与形心轴存在一定的偏移，桥面板越宽，剪力滞效应越明显，中心轴与形心轴的偏移越大，由于中性轴引起的偏移在计算截面正应力的时候并不能忽视。引入函数z0表示截面形心在中性轴坐标系中的偏移量。

悬臂梁在对称荷载作用下，梁截面内轴力为零，截面轴力平衡方程为：

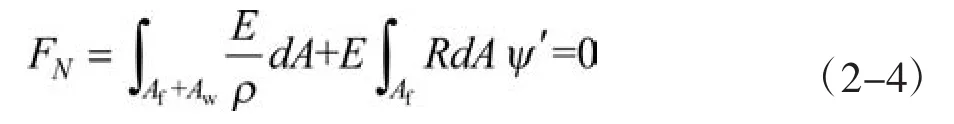
其中ρ为曲率半径，令质心在中性轴中的竖向坐标为z0，由式（2-4）可知：

由式（2-5），z0与主梁受弯曲率半径、E.Reissner函数和剪力滞广义位移ψ（x）有关，悬臂梁在受弯变形时各截面的曲率半径可近似认为相等；剪力滞广义位移ψ（x）的一阶导数用于描述影响剪力滞效应的附加弯矩，研究表明，悬臂梁在均布荷载作用下的固定端到L/4范围内为正剪力滞效应，端部集中荷载作用下全截面均为正剪力滞效应[5]，而能量变分法分析过程中必须保证在统一的坐标系内，因此偏安全地选取距固定端L/8截面处为全桥中性轴偏移量代表值。

3 变分方程推导及求解

3.1 基本变分方程的推导

根据位移方程，建立梁的力学几何方程，翼板正应变及剪应变为：

腹板正应变：

根据胡克定律，建立翼板及腹板的力学物理方程，桥面板为平面应力状态，则可得到翼板x方向应力，y方向应力，平面内剪应力和腹板方向应力：

式中：Ec为梁弹性模量；G为梁剪切模量；v为混凝土泊松比。

梁承受压弯外荷载时的外力势能：

式中：M及N分别表示作用在梁上的弯矩和轴力。

梁的体系应变能由翼板应变能和腹板应变能两部分构成：

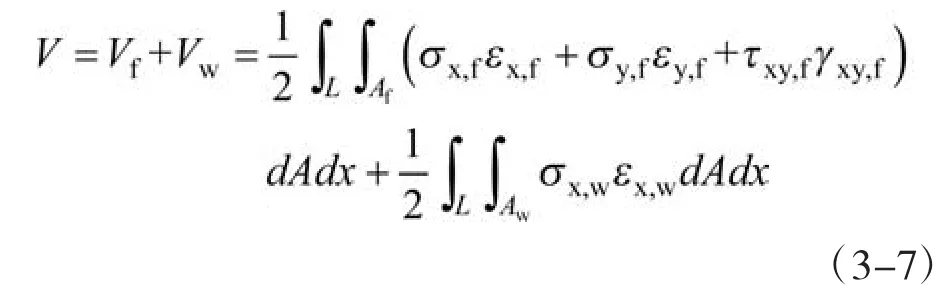
根据最小势能原理，在外荷载作用下，结构处于平衡状态。当有任何虚位移时，体系总位能的一阶变分δ为零，即：，它相当于泛函

整理后得如下方程：

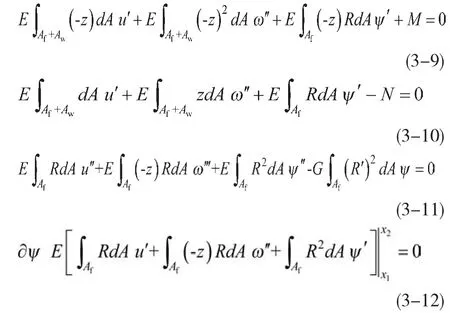
以A0、I0和Q0分别表示形心轴平面内双主肋梁的整体截面面积、整体截面对y轴的惯性矩以及整体截面对y轴的静力矩，其中； Q0=z0·A0；A0=Af·Aw，h与h′分别为桥面板和腹板中心到形心轴的距离。同时定义与E-Reissner函数R(y)相关的惯量定义：，，,则平衡微分方程及边界条件（3-9）～（3-12）可以改写为：

力学物理意义上，式（3-13）表示梁在z方向的平衡状态，式（3-14）则表示梁在x方向的平衡状态；式（3-15）表示由于剪力滞后效应导致翼板横截面出现应力分布不均匀状态，这种状态在板截面内的自平衡；式（3-16）表示广义剪力滞位移所需满足的边界条件。

3.2 承受自由端集中荷载的悬臂梁

考虑剪力滞后效应，对承受自由端集中荷载的悬臂梁，采用变分法推导的平衡微分方程加以推演。如图1（b）所示的等截面悬臂梁，自由端作用集中荷载T，作用位置位于梁主肋，距离梁截面形心δ处，荷载方向与水平方向夹角为θ。集中荷载在Ox方向上的投影N=-Tcosθ,在Oz方向上的投影P=Tsinθ。梁上作用均布荷载q。

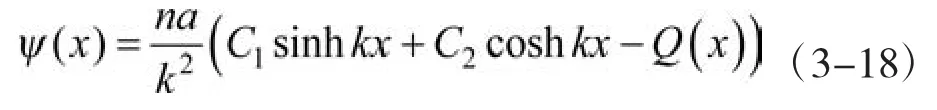
在悬臂梁的固定端，式（3-18）满足边界条件：ψ（x）=0；在悬臂梁的自由端（非固结），边界条件满足方程式（3-16）：由以上边界条件，可以求得悬臂梁最大纵向位移差函数ψ表达式（3-18）中的系数：

整理方程（3-19）和方程（3-20），可以得到梁变形微分方程：

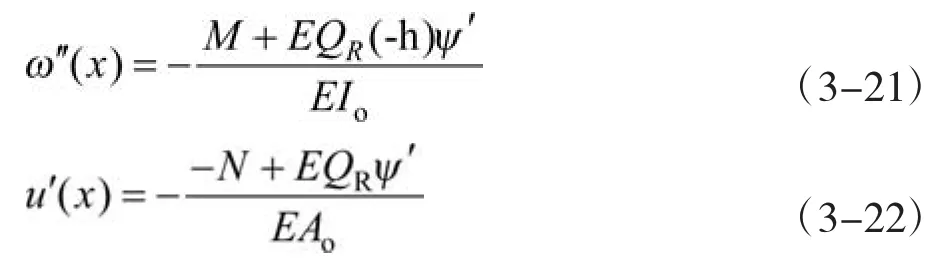
由式（3-21）与式（3-22）可见，考虑剪力滞后效应，梁的曲率-弯矩与线应变-轴力的关系已经不再符合欧拉-伯努利梁理论。在此，引入虚拟荷载来描述剪力滞后效应对结构的影响：附加弯矩；附加轴力。由于剪力滞后效应的影响，使得梁的有效刚度降低，增大了梁的变形。

结合式（2-5）与式（3-21），可知中性轴与形心轴偏移量:

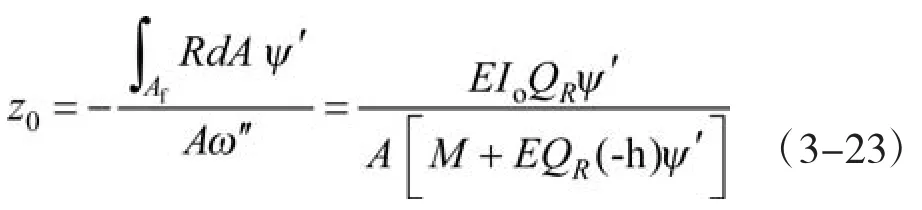
由前所述z0选取L/8截面处为全桥中性轴偏移，而式（3-23）看出，z0的取值需要先计算剪力滞广义位移ψ（x），而广义位移ψ（x）的取值与z轴的选取无关，因此暂认为中性轴偏移z0=0，即在形心轴坐标系内计算ψ（x），从而求得L/8截面处z0=0.08m。

将式（3-18）代入表达式（3-21），经过两次积分得到悬臂梁挠度曲线方程：

式（3-24）中的B1及B2为由悬臂梁固定端边界条件所确定的待定系数：

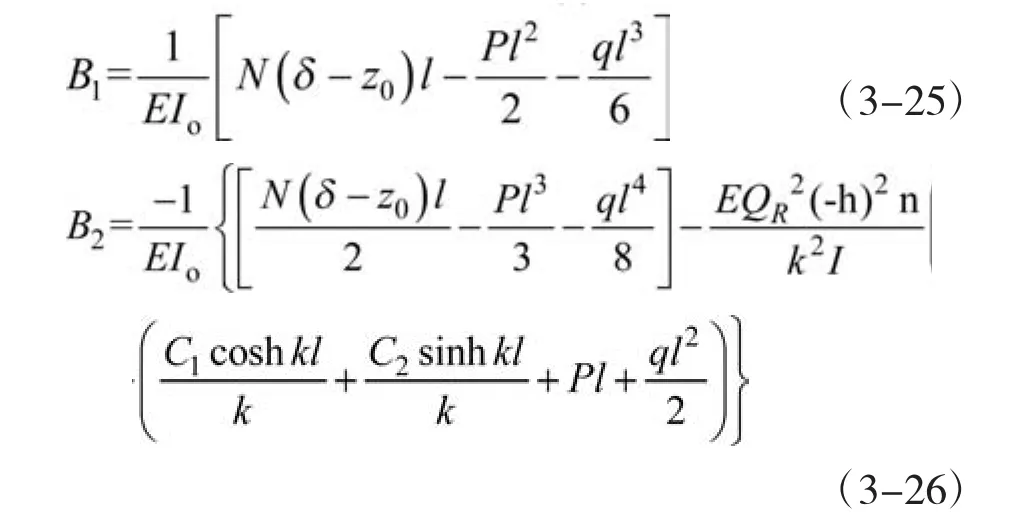
将式（3-25）、（3-26）及对（3-24）求一阶导数后，代入（3-24）式，便可以求得翼缘板的应力分布：

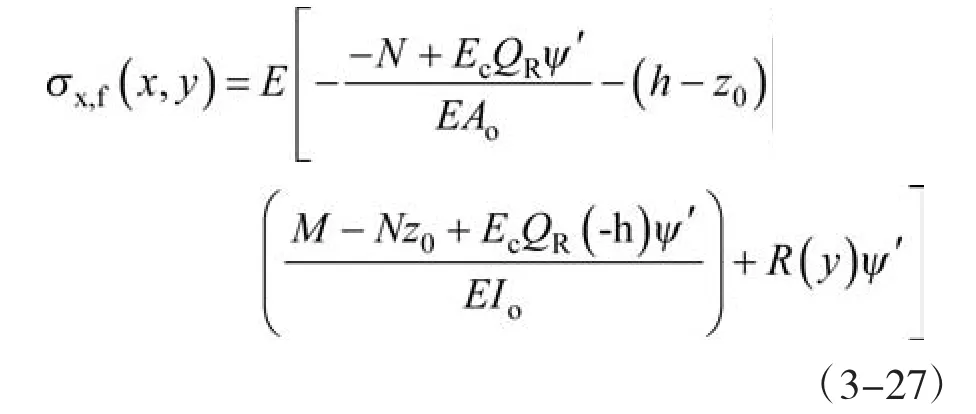
由式（3-27）便可以分析在压弯荷载作用下，翼板截面应力的横向分布规律。

4 数值算例

为了明确地了解悬臂施工阶段斜拉索索力对主梁的剪力滞效应的影响，本文以辰塔大桥为研究背景。该桥为双塔三跨单索面曲线矮塔斜拉桥(86m+160m+86m)，塔梁固结体系。桥面宽34.6m。主梁采用预应力混凝土π型梁截面。根据设计说明，模型中主梁材料C55混凝土的容重取25kN/m3，弹性模量E取值3.55×104MPa，泊松比取0.167。预应力钢绞线弹性模量取值1.95×105MPa，一号索拉索张拉应力控制为3750kN。采用结构有限元计算软件Ansys进行三维实体模型的建立和仿真分析，主梁采用实体单元，通过自动网格划分形成有限元模型。主梁在塔根处截面固定约束。全桥有限元模型如图2所示。

图2 ANSYS有限元模型示意图

在Ansys中利用PATH命令可得桥面板内特定截面内沿横向分布的节点正应力[6]，同时利用式（3-27）计算桥面板正应力，进行对比分析。

图3 悬臂梁L/8截面顶板应力比较

图3分别列出了本文方法计算的顶板各点正应力与ANSYS有限元数值解，由图中可以看出，本文方法计算结果与有限元结果基本吻合，说明了本文中关于E.Reissner函数和中性轴偏移的假设是正确的。

图中红线部分代表了不考虑中性轴与形心轴偏移的能量变分法的计算结果，若不考虑中性轴与形心轴偏移，剪力滞系数明显偏小，同时在桥面中线部分顶板甚至出现了拉应力，这显然与事实不符，考虑中性轴偏移的情况下，等效于添加了一个附加弯矩Nz0，使顶板正应力提高，进一步验证了本文假设和计算结果的正确性。

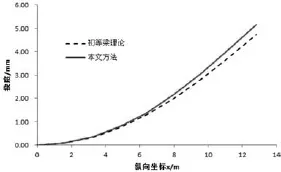
图4 悬臂梁在斜拉索及自重作用下挠度曲线

图4给出了1号索三张索力作用及自重作用下按初等梁理论及本文方法求得的挠度曲线。从图4可以看出，按本文考虑剪力滞效应的方法求得的挠度要明显大于按初等梁理论（不考虑剪力滞效应）求得的挠度，这是由于剪力滞效应会使梁翼缘板的面内刚度降低，从而必然导致挠度增大。按初等梁理论求得的跨中挠度为4.73mm，剪力滞附加挠度为0.43mm，剪力滞效应使挠度提高的幅度达到9.1%。可见，剪力滞效应会显著增大箱梁的挠度，工程实践中必须认真对待。

当然，该算例的挠度提高幅度并不适用于其他π型梁。对于具有不同参数的π型梁，由于跨度和荷载条件的不同，剪力滞效应引起的形心轴偏移也不同。工程实践中必须根据主梁具体截面尺寸和荷载条件计算剪力滞效应对挠度的提高。

5 结论

本文分析π型梁主梁剪力滞效应过程中，引入了剪力滞效应引起的中性轴偏移，假定翘曲位移函数和，建立了关于附加挠度的控制微分方程和边界条件。以辰塔大桥主梁为对象进行的悬臂梁计算表明，解析解与数值解吻合良好，从而验证了本文的理论分析方法和推导的公式是正确的。

以梁的弯曲理论为基础，利用平截面假定和中性层假设，推导出形心轴与中性轴存在一定偏差，计算表明，考虑中性轴偏差能够更加准确地描述主梁桥面板内的应力分布情况。

对集中荷载作用下悬臂算例的计算结果表明，剪力滞效应使挠度提高的幅度达到9.1%，对于具有不同参数的π型梁，由于跨度和荷载条件的不同，剪力滞效应引起的形心轴偏移也不同。工程实践中必须根据主梁具体截面尺寸和荷载条件计算剪力滞效应对挠度的提高。

[1]E.Reissner.Analysis of shear lag in box beams by the principle of the minimum potential energy.Quarterly of Applied Mathematics, 1946，4(3)：268-278.

[2]张元海，康喜东，林丽霞.箱形梁剪力滞效应分析中的翘曲位移函数及广义内力研究[J].计算力学学报，2012(6)：867-872.

[3]张士铎，邓小华，王文洲.箱型薄壁梁剪力滞效应[M].北京：人民交通出版社，1998.

[4]项海帆.高等桥梁结构理论[M].北京：人民交通出版社，2001.

[5]张士铎，王文洲.桥梁工程结构中的负剪力滞效应[M].北京：人民交通出版社，2004.

[6]胡晓伦，陈艾荣.ANSYS路径映射技术在结构分析中的应用[J].交通与计算机，2004(3)：86-89.

U442

A

1007-7359（2016）06-0107-04

10.16330/j.cnki.1007-7359.2016.06.041

赵傲（1990-），男，湖北仙桃人，同济大学土木工程学院在读硕士，研究方向：斜拉桥施工。