优化问题表征,提升“阅读与理解”能力——对解决问题“阅读与理解”板块的思考与实践
□浙江省杭州市北秀小学 倪惠娟
优化问题表征,提升“阅读与理解”能力——对解决问题“阅读与理解”板块的思考与实践
□浙江省杭州市北秀小学 倪惠娟
新人教版教材在“解决问题”的编写中,新增了“阅读与理解”和“回顾与反思”两大板块。笔者着重研究了“阅读与理解”这一板块,并进行了长期的实践与探索,总结出“三三三模式”,即“三步推进、三环相扣、三种策略”,来优化问题表征,提升学生“阅读与理解”能力,并取得了良好效果。
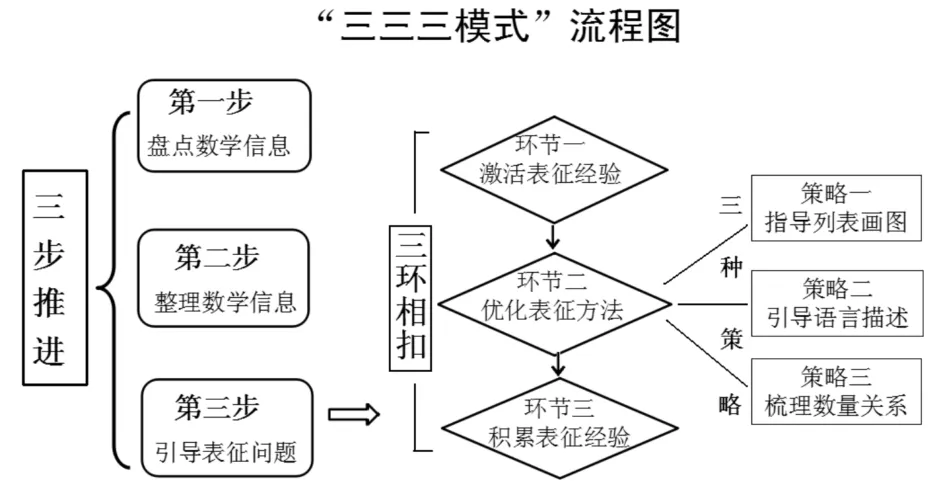
一、三步推进——掌握“问题表征”的基本流程
第一步:盘点数学信息——提升问题信息的“卷入度”。即收集整理题目中的已知信息和问题。面对这些问题,笔者借助“解题三问卡”来解决。要求学生在解题前必须做到“三问”。

如,小明是个晨跑爱好者,他平均每天早上要跑1200米,七、八两个月他一共跑了多少米?
面对这个问题,学生往往忽视“七、八月份都是大月”这个信息,很容易把它当做“30天/月”来计算。为此,笔者引导学生读题后,对照着“三问卡”,进行自问自答。最终学生都注意到了“七、八月份都是大月”这个信息,并成功解决了问题。
第二步:整理数学信息——凸显问题信息的“关联性”。笔者在教学中会常问:找到了这些信息与问题后,你是怎样发现它们之间的联系?通过一段时间的摸索和交流,创建了一些较实用的方法,如“自问自答法”和“自我暗示法”。
何谓“自问自答法”?就是先向问题提问,然后回答自己提出的问题。如:这道题要我们求什么,要求这个问题必须知道什么信息;这些信息和问题间符合什么数量关系;这道题有没有限制条件,有没有干扰信息;根据这几个信息,能求出什么问题,等等。
何谓“自我暗示法”?下面让笔者借案例来介绍吧。
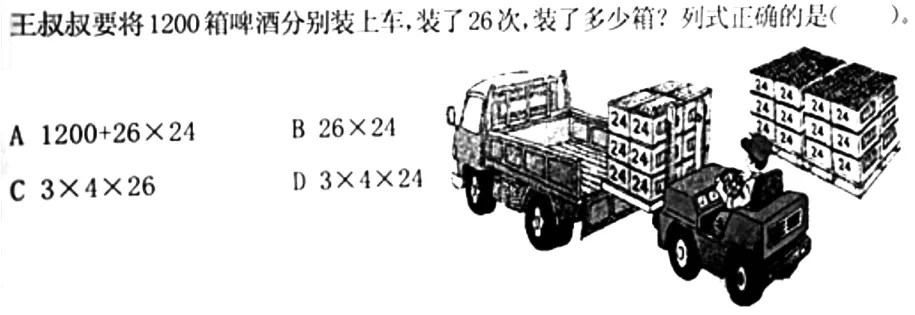
本题的信息以图、文两种形式同时存在,且无用的干扰信息“1200箱、每箱24瓶”都非常强势地吸引着学生的眼球,导致正确率极低。
同样的这道题,笔者给本校三年级下册的学生检测,就在题目下面添上了三句“提示语”。如:
1.我能从题中找出所有的数学信息;
2.我能排除掉和问题无关的信息;
3.我能理清问题和有关信息间的关系。
引导学生先对照“提示语”想一想,再做出选择,正确率竟然高达72.5%。
第三步:引导表征问题——构建问题信息的“脉络图”。引导表征问题,这是一个“去情境化、显数学化”的过程。这一步需要解题者将之前从问题中所收集到的信息,通过分析和加工,构建成属于自己的“问题认知结构”,并以自己喜欢的简洁、明了的形式呈现出来,进一步理清了问题中各部分内容间的逻辑关系,并顺利地解决问题。
二、三环相扣——经历“问题表征”的优化提升
掌握了“问题表征”的基本流程,接下来,学生们最需要掌握的是如何让“问题表征”更优化——既能舍去问题中的具体情节,又能形象地揭示出信息与信息、信息与问题之间的内在联系。
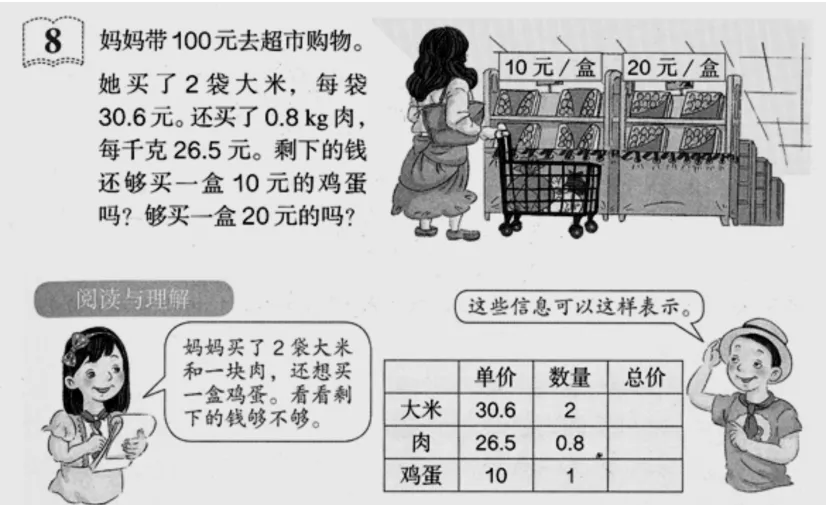
环节一:尝试——激活表征经验。出示题目后,笔者出示自主尝试的要求——
1.我能按“三问卡”的要求完成读题;
2.我能把题中重要的信息和问题,用简单的形式按顺序罗列出来。
学生在解决问题时,应该学会把题中的信息和问题,用简洁明了形式“表征”出来的能力。笔者通过巡视发现,学生的表征主要有以下几种情况。
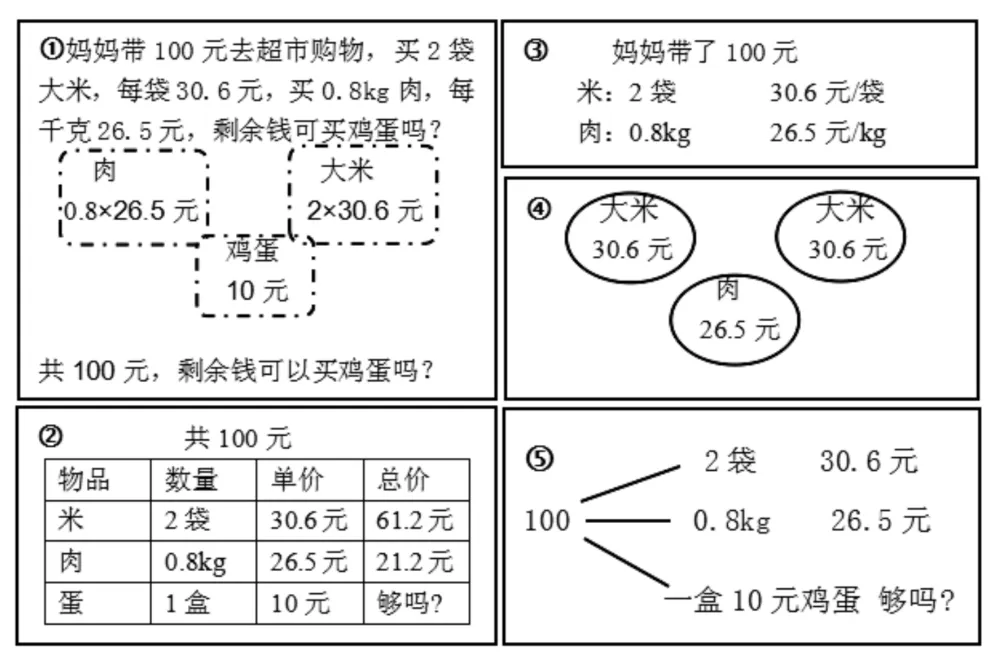
环节二:讨论——优化表征方法。笔者引导学生用两种眼光来评价这些作品,(1)欣赏的眼光,哪些地方值得我们学习;(2)批判的眼光,哪些地方需要改进。
通过交流讨论,达成了共识——
①号的作品不够简洁;③号、④号的作品虽然简洁,但不够完整,如④号作品既缺信息又缺问题,容易造成解题时的遗漏。②号和⑤号作品,都得到了同学们的认可,它不仅简洁明了地整理出信息和问题,并理出了信息和问题间的数量关系。
环节三:提炼——积累表征经验。
师:通过刚才的练习,你觉得咱们要把题中的信息和问题用简单的形式表示出来,需要注意什么?
生1:要把多余的文字,没用的信息排除掉。
生2:我们还要用最简单的形式,把重要的信息和问题都理出来,最主要是让自己一眼就看明白。
生3:最好还能反映出其中的数量关系。
师:是呀,那有哪些表示的形式呢?
生:可以列表格,可以画图,也可以用文字简单描述等等。
师:是的,当我们在解决问题时,尤其是碰到无法解决的问题时,就可以先把题中的信息和问题用“列表格、画图、或文字等”简单明了的形式表示出来,再来分析解答。
三、三种策略——掌握“问题表征”的基本形式
除了上面教学片断中提到的“列表、图文”表征外,常见的表征形式主要有以下几种——
策略一:指导列表画图——外显问题表征。图、表具有直观形象的特点,可以帮助学生简洁、明了地表征问题,提高解决问题的能力。这也是问题表征的常用方法之一。
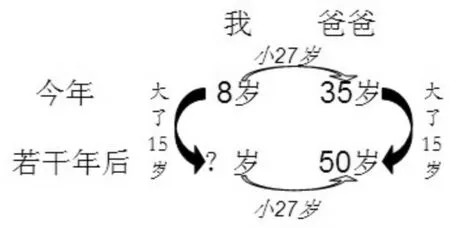
如:我今年8岁,爸爸今年35岁。爸爸50岁时,我多大?
这题有一定的难度,但如按之前的“三步推进”法,先让学生完成信息的收集,再引导学生用画图或列表的方法把信息和问题整理清楚,再来解决就变得容易多了。

今年年龄若干年后年龄我 爸爸8 35? 50
策略二:引导语言描述——完善问题表征。让学生用自己的语言把题目中的信息、问题逐一描述出来,把题目内容转化为鲜明的有声言语活动,使学生对题目的结构意义达到正确完整的理解。
例如:果园里有桃树、梨树各9棵,苹果树和梨树同样多,三种树共有多少棵?
笔者引导学生有意识地用自己的语言来复述题意,或提出不明白的地方。
生:“果园里有桃树、梨树各9棵。”也就是说“果园里桃树有9棵,梨树也有9棵。”他边演示边板书:桃9棵梨9棵
“苹果树和梨树同样多”就是说“梨树有9棵,苹果树也有9棵”。说着在原有板书后面添上:苹果9棵。
最终的板书呈现为:桃9棵梨9棵苹果9棵
通过这样的语言描述加上简单记录,孩子们脑中关于信息和问题的表征变得更清晰完善了。
策略三:梳理数量关系——优化问题表征。对于一些“骨架”较清晰的题,我们也可以从寻找题中最基本的“数量关系”入手来突显问题表征。

例如:新人教版五有题。
这题的错误率较高,主要错误有:20÷2+4;(20-4)÷2;20×2—4。出错原因,有的是找不准看做“1倍”的量,有的是找不准“3倍”对应的量,且不理解“多”与“少”的真正含义。为此,笔者引导学生先梳理数量关系,再来解答。
师:请找出关键句读一读。
根据学生回答板书:白色皮比黑色皮的2倍少4块
师:你能把这句话翻译成数量关系式吗?(简单的讨论后很快有了结果)
白色皮+4=黑色皮的2倍
黑色皮的2倍-4=白色皮的块数
黑色皮的2倍-白色皮=4
在此基础上,学生顺利地解答了问题。
所以,在解决问题的教学中根据问题的类别联想数量关系式,根据条件或问题叙述数量关系式,数量关系式的填空等练习也是可以借鉴使用的。

