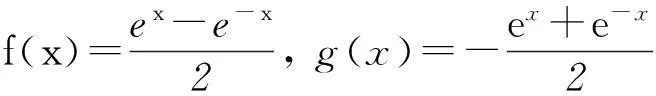单选题中比较大小的常用方法



单选题中比较大小的常用方法

◇内蒙古王志成

本文通过归类举例，说明解决单选题中的比较大小问题的4种常用方法,以切实帮助读者理清解题思路,掌握解题中的一些技能、技巧.

1排除法

在读懂题意的基础上,根据题目的要求,先将明显的错误或不合理的备选答案逐个地排除,最后得出正确的答案,这种解答单选题的方法称为排除法.

Aa

Cb

2作差比较法

比较大小,最常用最基本的方法就是作差比较法.“作差—分解因式—比较与0的大小关系”,这是运用作差比较法的基本解题步骤.

Af(x1)

Bf(x1)=f(x2);

Cf(x1)>f(x2);

Df(x1)与f(x2)的大小不确定

3利用指数函数、对数函数的图象和性质

比较有关指数式、对数式的大小时,要注意指数函数、对数函数的图象与性质的灵活运用.此外,要特别注意数字“0”和“1”在比较大小问题中的桥梁作用.

类似分析,由(1/2)b=log1/2b可得b∈(0,1);由(1/2)c=log2c可得c∈(1,+∞). 因a>0,b>0,所以a>-b，即2a>2-b，2a>(1/2)b,所以可得log1/2a>log1/2b，所以ab>a.

4利用抽象函数的性质

灵活运用抽象函数的性质(如单调性、奇偶性、对称性等),可以迅速求解与抽象函数有关的比较大小问题.

Af(2)

Bg(0)

Cf(2)

Dg(0)

①

所以f(-x)-g(-x)=e-x.

由f(x)是奇函数得f(-x)=-f(x),由g(x)是偶函数得g(-x)=g(x),于是

-f(x)-g(x)=e-x⟹f(x)+g(x)=-e-x.

②

联立式①、②解方程组得

(作者单位：内蒙古包头市包钢四中)