认知风格、中央执行负荷影响算术估算的策略选择适应性：行为与眼动证据

司继伟刘亚琼 贾国敬 黄碧娟（山东师范大学 心理学院，山东 济南 250014）



认知风格、中央执行负荷影响算术估算的策略选择适应性：行为与眼动证据

司继伟*刘亚琼 贾国敬 黄碧娟
（山东师范大学 心理学院，山东 济南 250014）

摘 要：随机选取212名大学生为被试，采用眼动技术考察了认知风格、中央执行负荷对算术估算策略选择适应性的影响。结果显示，中央执行负荷与认知风格联合作用于个体的估算策略选择，其作用过程受到算式呈现方式及策略自身特征的影响，而中央执行负荷更可能通过认知风格间接作用于估算策略运用，具体表现为场独立认知风格个体在负荷条件下较场依存认知风格个体的策略选择适应性更优。

关键词：认知风格；中央执行负荷；估算；策略选择适应性

一、引言

在实际生活中，大量的计算并不需要得到精确的结果，良好的估算能力是人们在日常生活中运用广泛的基本数学能力。估算是计算估计的简称，在中国传统的加减乘除口诀的基础之上通过心算等方式来进行的不需要精确结果的数学计算方式，这种方式具有一定的模糊性，属于个人技巧性的心理活动。［1］1980年以后，研究者已经在算术估算的类别、估算的发展状况、估算加工的脑基础、估算策略的种类以及估算能力与后天努力等众多领域做了很多研究。［1-5］现阶段很多专家对通过相关任务研究估算的执行策略的方法持保留看法，个体对问题的理解方式是多样的，单纯地考察具体策略的使用并不能够反映策略运用能力的全貌。以往许多研究已经发现，在数学问题解决过程中，人们会根据不同的情境选择使用不同的解决策略，而选择出一种快速又准确的策略会大大提高问题解决的效率。Verschaffel等人将这种既快又准的策略选择称为策略选择适应性。［6］这一观点的提出为研究者考察个体策略运用的灵活性和有效性提供了理论基础。

已有研究发现，策略适应性具体受情境因素（任务环境、成功基础率等）、群体因素（不同年龄、不同家庭收入等）以及个体差异因素（加工速度、工作记忆等）等影响。个体的策略选择具有一定的限制因素，中央执行系统在整个过程中起到主导作用，如实现策略的调配、选择和处理等。Schunn和Reder发现，个体的策略适用性受到任务复杂程度与工作记忆的影响［7］；De Rammelaere通过研究发现，中央执行系统对于估算问题的策略选择干预结果不同，这与估算问题的难易程度相联系［8］；Imbo等人曾运用选择/无选方法结合双任务范式，要求被试估算（乘法）同时，中央执行负荷对策略执行的影响程度是不同的，对复杂上调策略的影响大于下调策略。［9］现有执行功能与算术认知策略的研究大多采用相关设计，并将执行功能进行分离，但工作记忆能力是完成不同执行功能任务共同所需要的，将执行功能进行分离来观察对估算策略运用的影响程度是不全面的。本研究拟对中央执行负荷进行操纵，并对负荷水平进行更加严格的区分。

心理学家维特金于1940年建立的场独立/依存的概念体系，认知风格成为心理学家研究的重点。认知风格具有一定的偏好性，对于信息的处理过程是伴随着不同的认知风格，每种认知风格处理信息的方式都是不同的。场独立型认知风格拥有更高的思维灵活性，可以根据自己的思维对存在的信息进行加工，而场依存型恰恰相反，依靠经验来处理存在的信息，从另一个角度我们可以理解为思维活跃度是比较低的。策略选择属于信息加工范畴，认知风格可能对个体的策略选择适应性产生一定的影响。有研究指出，场依存的被试容易受到感觉通道变化的影响，使得场依存被试策略选择任务的速度和准确性都大幅地下降。［10］也有人发现，不同认知风格在一定程度上影响学习策略的多个加工过程，如信息加工、编码、储存、注意等策略等。［11-12］但在数学认知领域，目前相关研究还较少。曾有研究者发现认知风格与数学学习成绩紧密相关［13］，较优异的数学成绩与分析型的认知风格相联系，分析型认知风格与场独立型认知风格相关［14］；也有研究表明认知风格能够预测数学学习成绩［15-18］；此外，个体解决问题能力的强弱与元认知的关系非常密切［19-23］，在策略选择过程中，研究者也关注元认知的参与，尤其是自我监控能力在策略选择过程中的作用［24-25］。早期有研究发现，场独立被试在经过练习后能够学会调整自己的认知策略而场依存被试则没有表现出这样的趋势［26］；沉思型认知风格的个体，更加注重解决问题的正确率，所以倾向使用计数策略等缓慢但精确度高的策略［27］；Kolb等人发现，发散思维型个体在解决问题过程中更倾向于使用生成性而非从情境中提取策略［28］。由此看来，如今许多学者把认知风格不仅仅看作是人格的两个维度，更多地将其看作是反映个体在认知加工过程中所具有的元认知技能。另外，信息加工大多是在工作记忆系统这个平台上完成，工作记忆往往会对个体的策略选择表现产生影响。［29-30］那么认知风格是否会通过影响工作记忆而对算术策略的运用产生作用就成为值得探讨的理论问题之一。

精算和估算是算术中常用的两种方式，前者复杂的计算过程常以竖式方式进行表征，但算式呈现方式对估算的影响机制尚不明确。王明怡和陈英和在研究工作记忆中央执行对儿童算术认知策略的影响时记录了横式和竖式呈现对认知策略的影响［29］，但对于呈现方式的影响机制未作进一步探讨；Lemaire和Callies选取成年人和未成年人，观察二者在进行两位数加减计算的过程中所采用的策略类型，发现横竖两种呈现方式时的策略运用方式是不同的，采用横式的呈现方式时个体部分分解策略使用与全部分解策略使用的概率是相同的，而在竖式的估算过程中个体更多地是采用部分分解策略［31］。还有研究发现场独立型与场依存型认知风格可以作为视觉空间能力与工作记忆中的中央执行功能的测量依据。［32］估算问题呈现的方式不同，可能会造成不同的策略运用，被试可能会根据自己的偏好、资源分配情况来选择不同的策略去进行信息的处理和调配。所以，本研究将算式呈现方式也作为自变量，来探讨问题的空间表征方式与认知风格、中央执行成分三者对策略选择适应性的作用。

二、研究方法

（一）被试

被试选取某高校大学生212人，经过镶嵌图形测验和算术技能测验筛选，确定了31名高算术技能的场独立者与30名高算术技能的场依存者。在场依存的30人之中有3个人在眼动仪的测试实验中因不符合任务要求而被剔除，最终参加实验的人数确定为58名，其中场独立者31人，场依存者27人，视力或者矫正视力正常。所有被试在实验完成之后赠送礼品。

（二）实验设计

以算术技能为协变量，采取2（场独立认知风格、场依存认知风格）×2（中央执行高负荷、中央执行无负荷、中央执行低负荷）×2（横式算式呈现方式、竖式算式呈现方式）混合设计，模拟反应时、判断标准、加工深度为因变量。

（三）实验材料及仪器

采用EFT测试方法，主要的测试内容为将形状比较简洁图形和形状繁杂图形的混合，测试从中挑选出形状简洁图形的能力。主要有三部分，第一部分为练习，可以根据这部分筛选未理解问题的无效试卷，剩下的两部分各有10道题，不同编号的分值是不同的，其中1、2计0.5分，3、4为1分，5、6、7、8、9、10计0.5分，一共24分。测试过程严格按施测指导语进行，每部分限时4分钟。

French算数技能测试方法［33］是一种非常先进的算数技能测试方法，其主要的测试内容是测试个体对两位数以上问题的计算的速度和精确性，这种能力还包括其对记忆的管理水平和连续性的测试。整个测试过程有两个分支测试部分，复杂加法和复杂减法、乘法，测试时间一共有4分钟，每部分2分钟，各含有60道题目。

估算任务为自编的任务两位数乘法题，主要的呈现方式有两种：一种是横向的呈现方式，共20道题；另一种是竖向的呈现方式，共20道题。在两种呈现方式的估算测试中，每种方式都有5道上调题和5道下调题，横式呈现方式和竖式呈现方式的数字间距是相同的。为了增加测试的严谨性，所有在测试中出现的问题都严格遵守下面的原则：（1）所有乘数的个位数不能出现0、1、5、9；（2）乘数与乘数之间在十位和个位上的数字均不允许相同；（3）使用过的乘数不能通过位置转换的形式参与到下一个问题中去；（4）所有试次的结果都要保持在四位数以内。

负荷任务采用数字干扰任务，是Ham和Kim双任务范式中的重要组成部分。［34］负荷情境主要有三种，每种负荷情境都是不同的，对数字的任务主要有连减、再认等操作。高负荷连减数字任务中，数字是随机抽取的，从1开始到9，组成一个三位数进行不断连减，随机抽取160个，最小为243，最大为981。低负荷数字再认任务，生成的是七位数。七位数不重复的，随机选出90个，随机出现在任务中。

EyeLink眼动仪，参数设置为：（1）头部允许转动的范围为正负15°；（2）校准模式选定为Hv9。一台兼容计算机（P4）控制着整个实验，所有的刺激反应都可以通过一台19寸彩色标清显示器看到，显示器的分辨率为800*600，距离为60 cm。

（四）实验程序

程序采用加拿大SR Research 公司开发的Experiment Builder 1.6.1软件编写，实验的条件分为高负荷、低负荷、无负荷三种，实验周期间隔一星期，每次持续时间为45分钟，负荷条件分别是最佳策略、上调策略、下调策略，每种负荷情境都要按照最佳选择—无选上调—无选下调的顺序进行，呈现的方式分为横式和竖式两种，被试平均分为两部分，分别进行横式和竖式呈现方式的估算。每个block后有5分钟的休息时间，所有被试都要完成6个block共120个trial，三个负荷情境的测试总共需要完成18个block共120个trial。每轮正式实验之前都要进行练习，以保证对实验的理解程度。

EyeLink 1000眼动追踪应用系统存在先天缺陷，在实验的过程中无法完成负荷任务的结果和估算的结果的记录工作，所以要求被试主动将估算的结果告知主持测试的人员，同时按下手柄的按钮，将在高负荷情境下的测试结果大声地告诉主持测试的人员，由主试记录。无负荷任务按眼动仪手柄进行反应，眼动仪记录相关的结果。实验流程如图1、图2所示。具体程序如下：（1）无负荷任务实验中被试只进行估算任务。首先呈现指导语，被试在理解指导语之后触动手柄，指导语消失，然后进行眼睛矫正。呈现空屏，时间为750 ms。之后进入估算题目，被试完成后按手柄进入下一题。（2）低负荷任务实验中首先呈现指导语，当被试理解了指导语的具体含义之后触动手柄，指导语消失，然后进行眼睛矫正，按主试指导完成。接着出现一个六位数字串，持续时间为1 s，要求被试记忆，然后呈现4 s注视点“+”。要求被试报告估算答案后按下手柄。然后呈现750 ms空屏，被试需要对某一数字是否出现在之前的六位数数字串之中作出判断，当判断完成之后，按一下手柄进入到下一个试次。（3）高负荷任务实验中首先呈现指导语，当被试理解了指导语的具体含义之后触动手柄，指导语消失，然后进行眼睛矫正，按主试指导完成。呈现数字1 s后消失，要求被试开始进行连减的出声思维。呈现4 s注视点“+”，期间要求被试一直保持连减。之后出现估算任务，要求被试出声报告答案后按手柄消失，估算同时尽量保持连减。然后呈现750 ms空屏，要求被试报告连减结果。完成后，按手柄进行下一个试次。

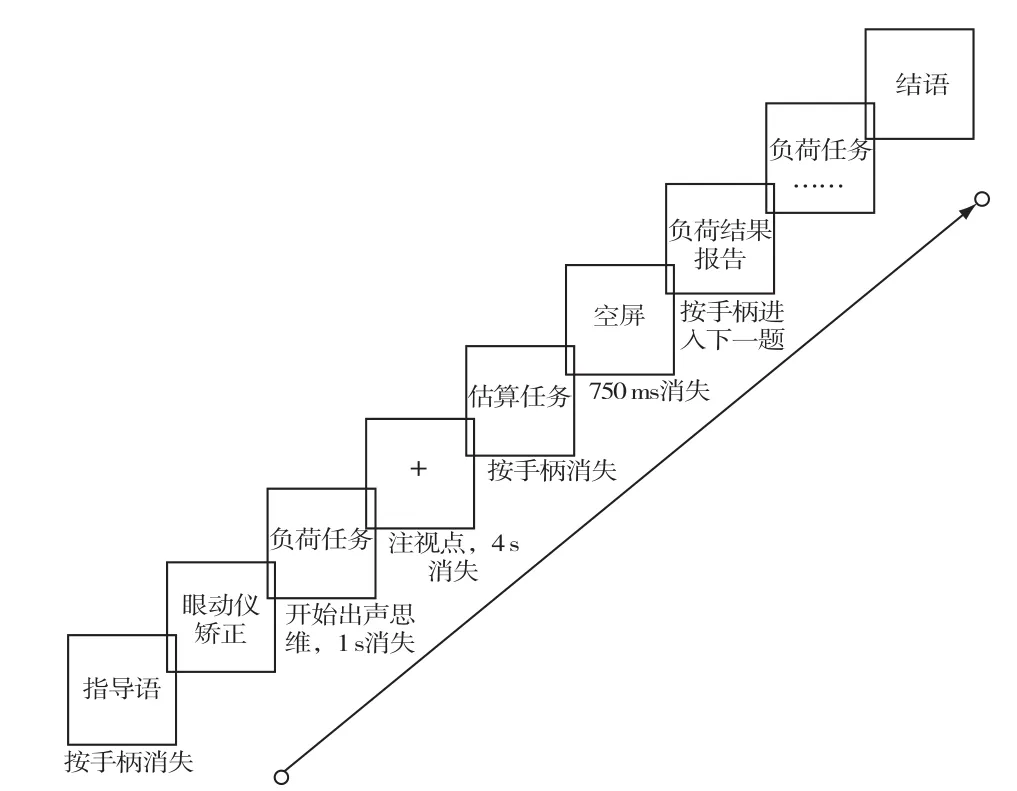
图1　有负荷情境任务block流程示意图

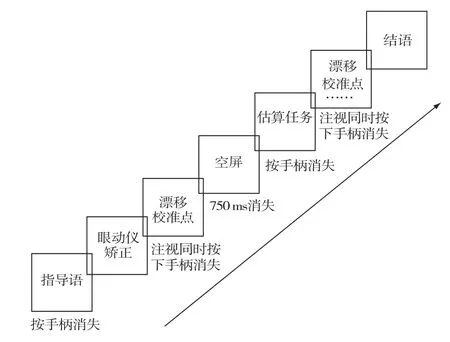
图2　无负荷情境任务block流程示意图

三、结果与分析

（一）模拟反应时

根据ASCM模型，策略的加工特征（策略使用的速度与准确性）影响策略的选择［35］131-176，即在某一特定问题上，如果两种策略的运用结果都是正确的，那么速度更快的策略更容易被采用。ASCM模型推理出了策略适应性公式：a策略有选条件百分比×a策略无选条件执行反应时+b策略可选条件百分比×b策略无选条件执行反应时。模拟反应时与实际反应时的差值越大，说明策略选择的适应性越大。［36］这样模拟反应时与实际反应时的差值可以反映个体在有选择条件下全部行为和相似行为之间的差异性。

不同认知风格、不同中央执行负荷、不同算式呈现方式下模拟反应时与最佳选择条件下反应时的差值见表1，协变量为算术技能，根据模拟的反应时间和实际的反应时间的差值，重复测量方差分析结果发现，认知风格主效应显著，F（1，55）=5.30，p=0.03，ηp2=0.09，场依存被试的策略适应性表现要差于场独立被试。算术技能主效应、中央执行负荷主效应、算式呈现方式主效应均不显著。交互作用差异不显著。

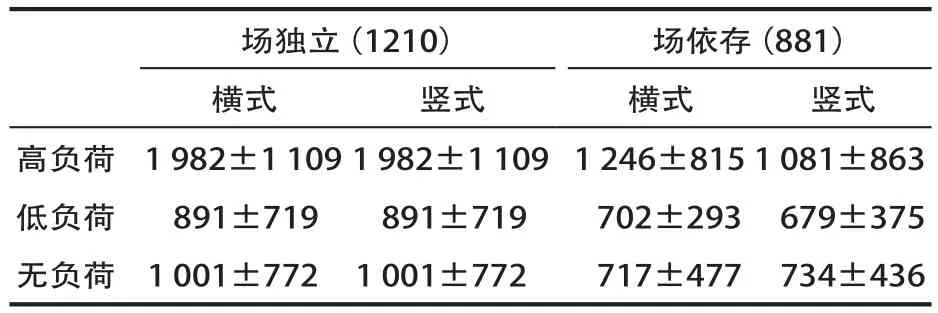
表1　不同认知风格、不同中央执行负荷、不同算式呈现方式下模拟反应时与最佳选择条件下反应时的差值（单位：ms）

（二）判断标准

信号检测论是关于人们在不确定情况下如何作出决定的理论。ROC曲线象征着一定的敏感度和特异度，许多研究者已经在判断标准理论基础之上开展算术策略运用的探索［37-38］，判断的标准越好，策略的适应性才越强。由于本研究只提供了两种策略供被试使用，依据信号检测理论，最佳选择条件下，我们将上调定义为信号，将下调定义为噪音，上调题中选择上调策略则为击中，上调题中选择下调策略则为漏报，下调题中选择上调策略则为虚报，下调题中选择下调策略则正确否定。在ROC曲线中，越往左上角说明被试的判断越准确，ROC曲线下的面积AUC越大说明被试的判断效果越好。不同认知风格与不同中央执行负荷条件下的ROC曲线参见图3。

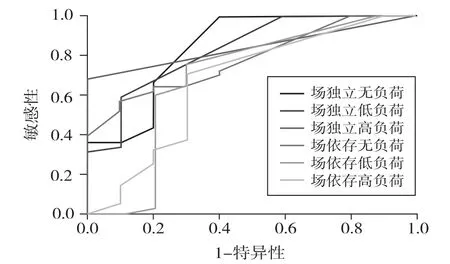
图3　不同认知风格个体的ROC曲线

对ROC曲线下面积AUC进行描述性统计，结果见表2及图4。认知风格受到负荷情境的影响，场依存被试判断标准差于场独立被试，说明场独立被试受外界因素的影响较少，影响信息处理的主要因素为外部线索。

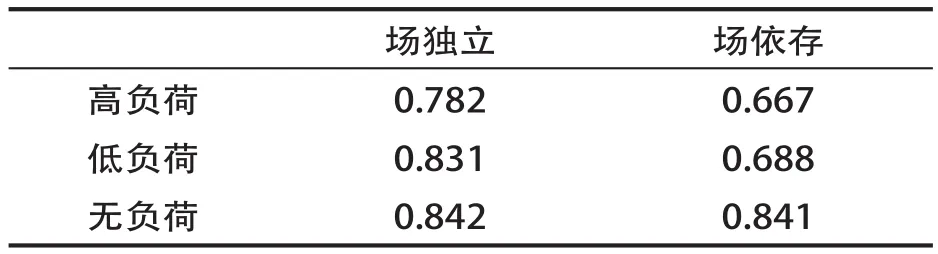
表2　不同认知风格、负荷条件下的AUC值

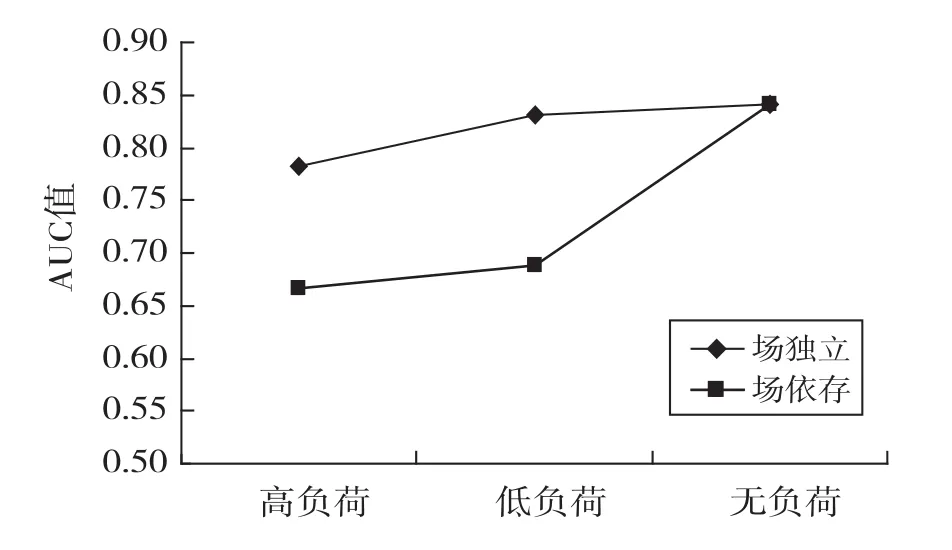
图4　不同认知风格、负荷条件下的AUC值

（三）加工深度

对于一个特定的被试个体来说，在特定的情境之下，针对某一指定的问题，个体总是有意或者无意地选择最准确或者最快速的策略来解决问题，研究者称之为策略适应性。［6］例如，一个问题可以有多种解决方法，但是上调策略能够既快又准地解决问题，那么个体选择上调策略解决问题的选择过程是适应的。在本研究范式下，我们选用策略选择的正确率来衡量策略适用性，正确率越高，则越适应。

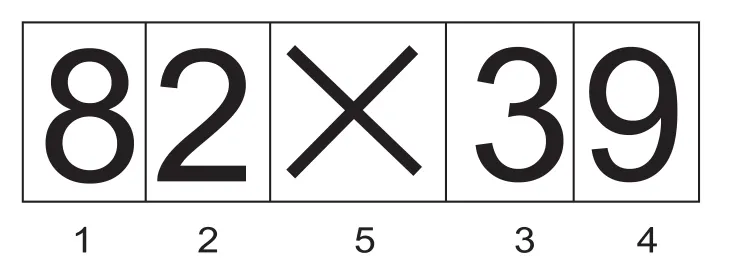
图5　乘法估算任务的兴趣区示意图

眼动证据需要使用眼动仪处理软件进行详细的手动形式的划定，划定的对象主要是兴趣。根据要研究的问题，将兴趣区按照图5方式划分为五部分，因乘号并非我们所关注，我们将兴趣区域分为1、2、3、4等四个部分，四部分分别代表两个乘数的不同的小数位。在眼动指标中，对兴趣区（1、2、3、4）的信息将有助于被试选择恰当的信息，根据以往研究，对于区2、区4数字的观察和加工有利于被试作出正确的策略选择，我们将加工深度定义为被试在单位时间内对兴趣区观察的次数，并将加工深度作为策略选择适应性的眼动指标。具体结果详见表3。

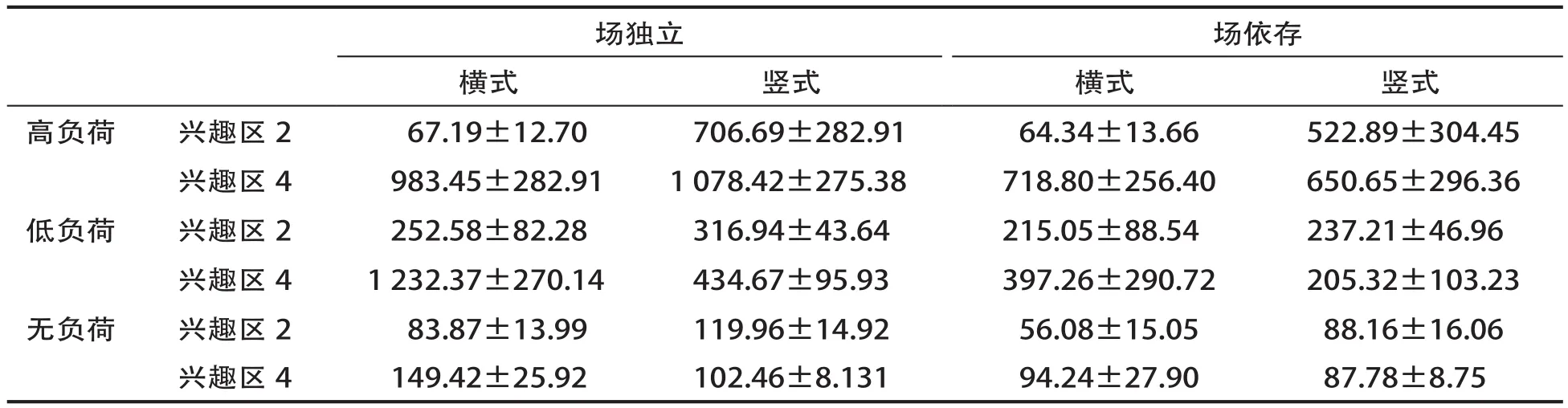
表3　不同认知风格、不同中央执行负荷、算式呈现方式以及不同兴趣区条件下的数字加工深度（单位：次/分钟）

重复测量方差分析结果显示中央执行负荷情境主效应显著，F（2，54）=2.66，p=0.03，ηp2=0.12，LSD结果表明，低负荷和无负荷之间，高负荷和无负荷之间差异显著。认知风格主效应边缘显著，F（1，55）=3.56，p=0.06，ηp2=0.06，场依存（278.65）个体策略选择适应性要差于场独立（460.67）个体。兴趣区差异显著，F（1，55）=9.57，p=0.003，ηp2=0.15。算术技能效应和算式呈现方式主效应不显著。

中央执行负荷和认知风格之间交互作用显著，F（2，54）=3.84，p=0.03，ηp2=0.12。通过简单的交互效应分析发现：在横式呈现方式情境下，被试对低负荷问题的加工程度最深；在竖式呈现方式情境下，被试对高负荷问题的加工程度最深。结果参见图6。

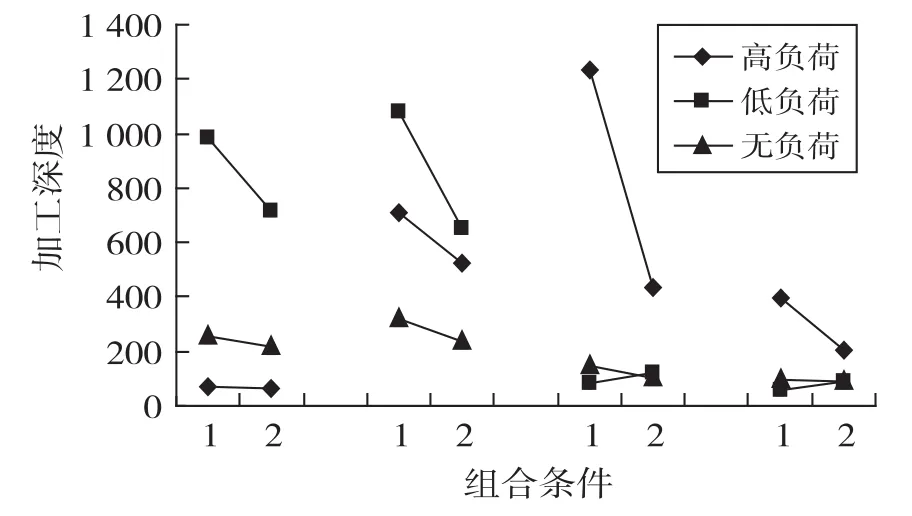
图6　认知风格和负荷两种形式非常简单的交互效果的测试

兴趣区与中央执行负荷之间的交互作用显著，F（2，54）=4.04，p=0.02，ηp2=0.13。在2（场独立、场依存）×2（横式呈现方式、竖式呈现方式）组间四种交互组合方式分析之下，我们发现区4在负荷情境下的加工程度（注视次数）是最深的。结果参见图7。

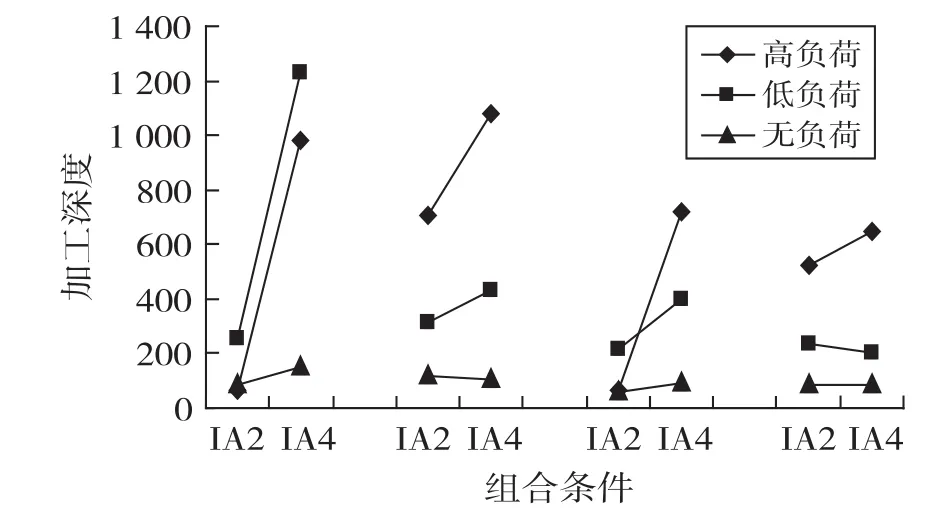
图7　中央执行负荷与兴趣区的简单交互效应检验

四、讨论

认知风格会对信息处理过程造成影响，造成结果产生不同的可能是通过认知过程来实现的，以策略运用的速度性和准确性指标，并不能全面反映策略运用的实际能力。本研究着眼于探究认知风格与认知过程之间的关系。目前关于策略选择的理论假设与研究范式的不同，策略选择适应性的研究领域是缺乏有效定义的，很多研究方法只能通过相应的指标来表现策略的适应性特征。

在估算中，场独立认知风格个体的表现优于场依存认知风格个体，其差异主要表现在策略选择适应性上，说明认知风格在一定程度上会影响到策略选择的适应性，与以往的研究结果具有一致性。［39］策略特征比问题表征更加复杂，在策略选择适应性模型中，策略特征与问题表征个体在头脑中存在一个信息库，被试个体往往是根据问题表征来选择策略的。场独立个体认知改组的能力强，在策略选择中往往倾向于摆脱场提供的信息，根据自身内部线索感知进行问题解决，能够更快速准确地分辨出策略的加工特征，较少受问题表征的影响。而场依存个体容易受到场提供的线索的影响，策略选择适应性较差。另一方面，根据策略选择及发现模型，元认知机制和联结机制都能够促进策略适应性的发展。个体对策略的运用的有效性上较为缺乏，另一个角度我们也可以认为元认知所处的水平可能较低。［40］152-178，440-447元认知所具有的一项重要功能——调控策略选择，可能与策略选择适应性密切相关。［6，41-42］本研究中，我们认为，场依存认知风格个体可能较场独立认知风格个体在元认知监控能力上存在差异。场独立认知风格个体能够从整体上把握问题解决的策略，并随着情境的变化不断进行策略的调整，更好地了解问题与策略之间的相互作用；而场依存认知风格个体不能够随着情境的变化及时选择适合的策略，对任务的认知加工过程中信息的编码与提取水平较低，从而造成策略选择适应性的明显差异。

其次，中央执行功能通过认知风格来影响策略选择适应性。早期认知风格的研究模式主要为洋葱模型，认知风格从内到外分别是认知人格层、信息加工层、教学偏好层。最外面的教学偏好层对存在的信息有一个偏好性的选择，而中间的信息加工层则主要是指个体信息处理的方式，洋葱模型内部的是认知人格层，主要作用于中间的信息加工层，与外界信息没有直接的联系。中央执行功能作为工作记忆的核心部分负责认知的协调、选择、分配等功能，认知人格层对中间的信息加工层有限制作用，同时信息加工层受到认知人格层的支配。比如，言语型认知风格个体在对信息进行表征时更多地依赖工作记忆中的语音环路，而表象型认知风格个体对信息进行加工时更多依赖于视空模板。本研究中，我们认为，场独立与场依存个体通过工作记忆对信息进行操纵，同时受到贯穿信息加工过程的认知风格偏好的影响，表现为个体以某种特定方式对信息进行加工。工作记忆中的中央执行成分根据策略的加工特征等因素，对所选择的策略进行注意资源的分配来促进问题的解决，从而使个体表现出运用某种策略解决问题的外部行为结果。此外，策略转换代价的观点表明前一种策略的使用会对后一种策略能够产生影响。［43-45］策略间的转换需要消耗认知资源，当工作记忆负荷更多地占用中央执行功能，个体的策略选择适应性降低。在判断标准指标上，场依存个体在信息加工时注重对细节的加工，对认知资源的消耗强度更大，这就使得场依存个体受负荷的影响变得非常大，受到策略转变代价的影响也是非常大的，从而共同影响了策略选择适应性。

最后，本研究中前两个指标仅仅从行为层面提供了认知风格与中央执行对策略选择适应性的影响，为了更好地揭示三者的内在机制，我们选取了眼动指标。单位时间内的注视次数可以衡量视觉信息搜索的效率，场独立认知风格被试的注视次数大于场依存被试，说明场独立个体花费更长的时间找到问题的关键，寻求找出解决问题的最佳策略，实验结果也支撑了这一论点。场依存被试的策略选择适应性要差于场独立被试，场依存被试可能会受到中央执行负荷的影响，在加工深度指标（关注次数）中，场独立个体的策略选择的适应性表现优于场依存个体。中央执行负荷更可能对场依存认知风格被试起到干扰作用。在加工深度指标中，中央执行负荷和认知风格之间的交互作用通过简单效应分析，中央执行负荷、认知风格交互作用显著受到算式呈现方式的制约。在横式算式呈现方式情境下，被试对低负荷问题的加工程度最深；在竖式算式呈现方式情境下，被试对高负荷问题的加工程度最深。这可能由于低负荷任务与横式的呈现方式一致，前面呈现的负荷任务对后面呈现的估算任务产生抑制，因此需要更深层次的加工。竖式呈现方式可能较横式呈现方式具有新异性，相比低负荷与无负荷任务，在控制性参与的注意上所需要认知资源更多，所以需要深层加工。

基于本研究有关发现，中央执行负荷和认知风格共同作用于估算策略运用选择的适应性，这个作用过程受到算式呈现方式和策略本体特征的影响，中央执行负荷与估算策略选择没有直接的关系，前者主要是通过认知风格间接作用于后者的。

五、对数学教育的实际含义

在数学学习的教育过程中，从知识的掌握到问题的解决，策略都扮演着重要角色。教会学生如何学习成为现代教学的一项重要目标。算术估计能力作为数学能力的基础和核心部分，在儿童和成人生活和学习中普遍存在。我国在课程改革中也相当强调估算的重要作用，但对于在教学中如何引导学生开展估算学习人们却所知甚少。随着对数学估计的重视程度的增加，越来越多的教育研究者开始关注如何有效地促进个体的算术估计能力。本次研究主要测试了认知风格、中央执行负荷对估算策略运用选择的影响程度，对于教育方法的改革具有理论意义和实践指导意义。本研究与之前研究发现一致，即便是成人被试，策略适应性仍然容易受到负荷的影响。［46-47］这启示我们在教学过程中：（1）教学内容的呈现要充分考虑学生的认知负荷。根据认知负荷理论提出的“冗余效应”和“形式效应”，教学内容应该呈现核心的信息，并且利用学生的各种感觉通道以减少工作记忆的负担。具体来说，教师应注意合理安排不同教学内容之间的难度及编排排序，以最精简的认知结构形式或原理形式呈现给学生，减少多余信息对认知负荷的影响。同时教学设计的内容可以以整合的方式呈现，充分利用教学媒体，将教学内容以图片与声音结合的方式呈现，减少学习者以单一通道形式接受超负荷的知识。（2）教学过程的控制和操纵应符合学习者认知负荷量的特点。在新知识的学习阶段、早期数学教育以及面对数学基础较差的学生时，不要让学生在短时间内的学习强度过大，可随着学习的深入，教学难度缓慢增加。

此外，认知风格在中央执行成分影响策略选择适应性的机制中发挥着一定作用，所以在教学中除了重视外在教学形式，对学生个体特征差异的理解和把握也是实现有效教学的途径之一。不同认知风格个体其组织和表征信息的偏好不同，可以为组织适应学生认知风格特点的教学活动提供相应的参考。每个学生的认知风格都是不同的，老师应该尊重学生的认知风格，然后根据每个学生的认知风格的特点进行因材施教，通过针对性的教学指导激发学生对于知识的渴望。对于场独立认知风格的学生要多与其谈话，帮助建立内心的目标感和责任感，鼓励其自己提高独立思考能力，同时丰富这些学生的策略库，提高应对能力。对于场依存认知风格的学生，要多从外界环境入手，外界因素的改变能够从很大的程度上改变学生学习的积极性，对于提高学生的独立思考和独立判断能力起到重要的作用；对于其每一个进步都要建立正面的反馈系统，积极引导学生参与集体讨论和交流，将每种策略适用到不同的学习情境中，通过不断的变式练习，不断提高其策略选择的适应性，进而不断提高数学能力。

策略选择适应性过程存在对关键区域和有效区域的注意、编码、存储以及提取，所以在教学中训练学生如何准确定位有用信息应作为教学工作的重要内容，这就与学生的元认知能力联系到了一起。近年来，研究者开始从策略选择的元认知角度进行干预，提高个人克服困难的能力和调整自己的能力。［48-50］知识的储备虽然很重要，但是学生如果不能够掌握运用知识的有效策略，未能快速准确发现解决题目的关键特征，或无法利用长时记忆中相关资源对信息进行有效的加工，都会加重认知负荷并影响学习结果。在课堂上，学生在教师的指导之下制定符合自己能力和情况的学习目标和计划。在教学工作中，教师要与学生经常性地沟通，并对学生表示正面鼓励，提高学生自主学习的能力，培养学生主动发现问题的能力（如，学习方式、方法、途径），提高学生对自己的认识程度，改善自己，从而使学生不断取得进步。

六、研究局限与未来展望

策略运用是一项复杂的认知加工活动，本项目以被试的估算测试任务为主要手段，开展对策略运用适应性影响因素的研究工作。毋庸讳言，目前我们所开展的工作还存在一定问题，具体如下：

首先被试个体的筛选工作有疏漏的地方，筛选方式过于简单，只是单纯地采用镶嵌图形的测试方法进行筛选。同时被试个体的样本采集量较小，降低了外部效度，后期的研究可以考虑扩大取样范围，选择不同地区的被试进行比较研究，一方面验证已有的结论，另一方更全面地考察认知风格这一典型个体差异对估算策略使用的影响，提高结论的客观性和全面性。

其次，选择/无选法研究范式自身是存在不足的。在实验中，这种研究范式对估算乘法的可选条件进行一定的控制，这种控制可能会使得部分策略被排除，无法全面考察策略运用的全部状态，对于新策略的产生和发展过程也不能考察。

第三，中央执行系统的可分离性现阶段的争议非常大，未来在条件允许的情况下可以通过控制中央执行系统的具体功能来研究其对认知策略运用的影响方式。

最后，国内关于策略选择适应性的研究较少，相应的研究方法也存在很多不成熟的地方，特别是运用眼动方式进行策略适应性的研究，而现阶段无法将策略的选择和执行阶段分开。目前在数学认知和语言认知领域中已经出现了将眼动技术与ERP、fMRI或PET等脑成像技术手段结合起来的综合考察［51］，后期研究有必要全面充分地利用先进技术从行为和生理层面共同考察算术策略运用的内部机制。

参考文献

［1］司继伟.小学儿童估算能力研究［D］.重庆：西南师范大学，2002.

［2］Deheane S，Spelke E，Pinel P，et al.Sources of mathematical thinking：Behavioral and brain-imaging evidence［J］.Science，1999，284（5416）.

［3］Hanson S A，Hogan T P.Computational estimation skill of college students［J］.Journal for Research in Mathematics Education，2000，31（4）.

［4］Brade G A.The effect of a computer activity on young children’s development of numerosity estimation skill［D］.Buffalo：University of New York，2003.

［5］Dowker J.Early identification and intervention for students with mathematics difficulties［J］.Journal of Learning Disabilities，2005，38（4）.

［6］Verschaffel L，Luwel K，Torbeyns J，et al.Conceptualizing，investigating，and enhancing adaptive expertise in elementary mathematics education［J］.European Journal of Psychology of Education，2009，24（3）.

［7］Schunn C D，Reder L M.Another source of individual difference：Strategy adaptivity to changing rate of success［J］.Journal of Experimental Psychology：General，2001，130（1）.

［8］De Rammelaere S.The role of working memory in mental arithmetic［D］.Ghent：Ghent University，2002.

［9］Imbo I，Vandierendonck A.The development of strategy use in elementary school children：Working memory and individuals differences［J］.Journal of Child Experimental Psychology，2007，94（4）.

［10］Yan J H.Cognitive styles affect choice response time and accuracy［J］.Personality and Individual Differences，2010，48（6）.

［11］丁晓峰.中学生物理学习策略及其认知风格关系的研究［D］.开封：河南大学，2005.

［12］孔庆娜.初中生认知风格特点及其对学习策略与学业成绩影响的研究［D］.长春：东北师范大学，2007.

［13］Zhang L F.Thinking styles：Their relationships with modes of thinking and academic performance［J］.Educational Psychology，2002，22（3）.

［14］Singh H，O’Boyle W.Interhemispheric interaction during global-local processing in mathematically gifted adolescents，average-ability youth，and college students［J］.Neuropsychology，2004，18（2）.

［15］郭成，张大均.元认知训练对不同认知风格小学生应用题解题能力的影响［J］.心理科学，2004，27（2）.

［16］游旭群，张媛，刘登攀，等.小学生数学应用题解题水平影响因素的研究——视空间能力、认知风格及表征方式的影响［J］.心理科学，2006，29（4）.

［17］Alenezi D F.A study of learning mathematics related to some cognitive factors and to attitudes［D］.Glasgow：University of Glasgow，2008.

［18］Price S M.How perceived cognitive style，metacognitive monitoring，and epistemic cognition indicate problem solving confidence［D］.Raleigh：North Carolina State University，2009.

［19］Metcalfe A W S，Campbell J I D.Switch costs and the operand-recognition paradigm［J］.Psychological Research，2010，74（5）.

［20］Karpicke J D.Metacognitive control and strategy selection：Deciding to practice retrieval during learning［J］.Journal of Experimental Psychology：General，2009，138（4）.

［21］Akiyama K，Yamaguchi H.Task performance and metacognitive experiences in problem-solving［J］.Psychological Reports，2004，94（2）.

［22］McCormick C B.Metacognition and learning［G］//Weiner I B，Reybolds W M，Miller G E.Handbook of psychology：Vol.7 educational psychology.New York：Wiley，2003.

［23］刘伟方，司继伟，王玉璇.认知策略选择的元认知因素［J］.心理科学进展，2011，19（9）.

［24］刘伟方，华晓腾，封洪敏，等.策略运用能力的年龄差异：元认知监测与算术知识的作用［J］.心理发展与教育，2014，30（3）.

［25］张红段，王玉璇，司继伟.论认知风格与认知策略运用［J］.贵州师范大学学报（社会科学版），2013，（3）.

［26］李寿欣.关于场依存认知方式的理论及其理论模型修订［J］.西南大学学报（社会科学版），2008，34（1）.

［27］Siegler R S.Implications of cognitive science research for mathematics education［G］//Kilpatrick J，Martin W B，Schifter D E.A research companion to principles and standards for school mathematics.Reston，VA：National Council of Teachers of Mathematics，2003.

［28］Kolb A Y，Kolb D A.Learning styles and learning spaces：Enhancing experiential learning in higher education［J］.Academy of Management Learning and Education，2005，4（2）.

［29］王明怡，陈英和.工作记忆中央执行对儿童算术认知策略的影响［J］.心理发展与教育，2006，22（4）.

［30］Imbo I，Duverne S，Lemaire P.Working memory，strategy execution，and strategy selection in mental arithmetic［J］.The Quarterly Journal of Experimental Psychology，2007，60（9）.

［31］Lemaire P，Callies S.Children’s strategies in complex arithmetic［J］.Journal of Experimental Child Psychology，2009，103（1）.

［32］Rittschof K A.Field dependence-independence as visuospatial and executive functioning in working memory：Implications for instructional systems design and research［J］.Educational Technology Research and Development，2010，58（1）.

［33］French J W，Ekstrom R B，Price I A.Kit of reference tests for cognitive factors［M］.Princeton：Educational Testing Service，1963.

［34］Han S H，Kim M S.Visual search does not remain efficient when executive working memory is working［J］.Psychological Science，2004，15（9）.

［35］Siegler R S，Shipley C.Variation，selection，and cognitive change［G］//Simon T，Halford G.Developing cognitive competence：New approaches to process modelling.Hillsdale：Erlbaum，1995.

［36］Siegler R S，Lemaire P.Older and younger adults' strategy choices in multiplication：testing predictions of ASCM using the choice/no-choice method［J］.Journal of Experimental Psychology：General，1997，126（1）.

［37］Sarah S W，Meghan L M，Uta M，et al.Standardized assessment of strategy use and working memory in early mental arithmetic performance［J］.Developmental Neuropsychology，2008，33（3）.

［38］Hickendorff M，Putten C M，Verhelst N D，et al.Individual differences in strategy use on division problems：mental versus written computation［J］.Journal of Educational Psychology，2010，102（2）.

［39］王玉璇.中央执行成分、认知风格与成人算术策略运用的关系：来自估算的证据［D］.济南：山东师范大学，2011.

［40］Bjorkltmd D F.Children's thinking［M］.Belmont：Wadsworth/Thomson Learning，2003.

［41］Desoete A，Roeyers H.Off-line metacognition：A domain-specific retardation in young children with learning disabilities?［J］.Learning Disability Quarterly，2002，25（2）.

［42］黎坚，张厚粲.认知操作背景下在线元认知调节能力的特征［J］.心理学报，2006，38（3）.

［43］Schillemans V，Luwel K，Bulte I，et al.The Influence of previous strategy use on individuals' subsequece strategy choice：Fingdings from a numerosity judgement task［J］.Psychologica Belgica，2009，49（4）.

［44］Lemaire P，Lecacheur M.Strategy switch costs in arithmetic problem solving［J］.Memory and Cognition，2010，38 （3）.

［45］Metcalfe J.Metacognitive judgments and control of study［J］.Current Directions in Psychological Science，2009，18 （3）.

［46］Imbo I，LeFevre J.Cultural differences in complex addition：Efficient Chinese versus adaptive Belgians and Canadians ［J］.Journal of Experimental Psychology，Learning，Memory，and Cognition，2009，35（6）.

［47］司继伟，杨佳，贾国敬，等.中央执行负荷对成人估算策略运用的影响［J］.心理学报，2012，44（11）.

［48］Lam W Y K.Examining the effects of metacognitive strategy instruction on ESL group discussions：A synthesis of approaches［J］.Language Teaching Research，2009，13（2）.

［49］Schunk D H，Zimmerman B J.Self-regulation and learning［G］//Weiner I B，Reynolds W M，Miller G E.Handbook of psychology：Vol.7 educational psychology.New York：Wiley，2003.

［50］Swanson H L.Instructional components that predict treatment outcomes for students with learning disabilities：Support for a combined strategy and direct instruction model［J］.Learning Disabilities Research and Practice，1999，14（3）.

［51］Knops A，Thirion B，Hubbard E M，et al.Recruitment of an area involved in eye movements during mental arithmetic ［J］.Science，2009，324（5934）.

［责任编辑：江 波］

●史海钩沉：中国教育家研究

The Central Executive Load and the Individual’s Strategy Use Adaptability with Cognitive Style:Behavioral and Eye-tracking Evidence

SI Ji-wei LIU Ya-qiong JIA Guo-jing HUANG Bi-juan
(School of Psychology,Shandong Normal University,Jinan,Shandong 250014,China)

Abstract：In this study,we employed eye movement tracking techniques to explore the effects of cognitive style and the central executive load on strategy use adaptability during arithmetic processing.212 college students were randomly selected for the research.The results showed that the central executive load combined with cognitive style affect the choice of arithmetic estimation strategies by the equation presentation format and characteristics of the strategy,while the central executive load is more likely to affect estimate strategy use through cognitive style indirectly,which means that the individual with better strategy use adaptability of the field independent cognitive style in load condition outperforms the individual of the field dependent type.Key words：cognitive style;central executive load;estimation;strategy use adaptability

*通讯作者：司继伟，E-mail：sijiwei1974@126.com。

中图分类号：G44

文献标识码：A

文章编号：2095-7068(2016)01-0085-11

收稿日期：2015-06-10

基金项目：国家自然科学基金项目“算术估算策略运用的认知与神经基础”（项目编号：31371048）、山东省自然科学基金项目“中央执行功能对算术估计策略选择的影响”（项目编号：ZR2010CM059）的阶段性研究成果。

作者简介：司继伟（1974—），男，山东聊城人，博士，山东师范大学心理学院教授、博士生导师，主要从事认知发展与学习研究。