超低轨航天器气动设计与计算方法探讨

胡凌云张立华程晓丽靳旭红丁延卫

（1航天东方红卫星有限公司，北京 100094）（2中国航天空气动力技术研究院，北京 100074）

超低轨航天器气动设计与计算方法探讨

胡凌云1张立华1程晓丽2靳旭红2丁延卫1

（1航天东方红卫星有限公司，北京 100094）（2中国航天空气动力技术研究院，北京 100074）

对于运行在150～300km高度的超低轨航天器，气动力是轨道与姿态控制须考虑的主要扰动因素。文章首先剖析了超低轨航天器气动构型的关键要素，提出了本体截面与长细比、翼面形状与布局的设计准则；从来流特性、气体－表面作用、航天器物理特性3个方面阐述气动建模的内容与方法；综合运用射线跟踪平板（RTP）与试验粒子蒙特卡洛（TPMC）2种自由分子流模拟方法，提出一种适合工程应用的气动计算与飞行仿真流程。最后，以重力梯度测量卫星为实例，开展了初步的方案设计、模型确认与方法探索，验证了气动建模与计算流程的正确性。文章所提出的气动研究思路，对超低轨航天器的气动设计、计算等工作，均具有一定的参考意义。

超低轨航天器；气动设计；气动建模；气动分析；重力梯度测量卫星

1 引言

近地轨道上运行的航天器，尤其是150～300km高度的卫星，处于自由分子流状态的地球高层大气之中，气动力与气动力矩是影响其轨道与姿态的最大扰动因素之一［1－2］。近年来，随着高分辨率对地观测卫星、快速响应卫星、微纳卫星星座等任务的增加，航天器运行高度不断向超低轨延伸，气动研究已变得越来越重要。目前，超低轨还没有准确定义，它通常是指高度在150～300km的热层大气底部区域。该轨道运行的航天器具有高分辨率、低发射成本、快速部署、容易清除等优势，但必须进行气动设计。国外已经发射的超低轨航天器，如“地球重力场与海洋洋流探测”（GOCE）卫星，特别采用了扁平、细长构型以减少气动阻力，配置了气动翼面以满足姿态稳定性要求。

在轨航天器气动问题，属于稀薄气体动力学中的自由分子流领域。从20世纪50年代开始，国外就开展了相关研究，但大多停留在使用简单的弹道公式计算大气阻力的层次上，关注重点是阻力系数与大气模型，目标是估算轨道扰动或在轨寿命。此后，基于稀薄气体动力学发展了一门新的学科“航天空气动力学”，主要是研究发射上升段和再入返回段等过渡流空气动力学问题［2］，应用目标是运载火箭、高超音速飞行器、返回式卫星、飞船返回舱、火星着陆器等航天器，采用的方法是直接仿真蒙特卡洛（DSMC）方法，分析工具是大型计算机与并行软件系统。但是，DSMC方法由于考虑分子间碰撞问题，须耗费大量计算时间与资源，并不适合无碰撞项的自由分子流问题。文献［3－4］中介绍了欧洲航天局（ESA）开发的地球卫星稀薄气体动力学建模系统（Rarefied Aerodynamic Modeling System for Earth Satellites，RAMSES），并使用该软件对欧洲遥感卫星－1（ERS－1）、“环境卫星”（ENVISAT）、GOCE等航天器进行了气动分析。RAMSES程序采用试验粒子蒙特卡洛方法（TPMC）和射线跟踪平板（RTP）方法，没有考虑分子间碰撞与计算域网格，大幅度减少了计算量，但是其实现方法并未被公布。文献［5］中使用自由分子流软件（FREEMOL），对2颗编队飞行的“重力校正和气候实验”（GRACE）卫星进行了气动差异性分析。不过，其中所采用的平板法，只适用于简单的凸形体，不支持多次反射等分子流模拟问题。目前，国内针对这方面的研究较少，而且都是围绕GOCE卫星开展的［6－9］，因而仍然缺乏合适的工程计算方法及简便工具来支持实际的航天器研制工作。

本文基于国内外的研究成果，从设计、建模与分析角度，探讨适合工程应用的超低轨航天器气动研究方法，并以重力梯度测量卫星为例开展相关的应用与验证工作。

2 气动构型要素分析

航天器气动构型是一项系统顶层的设计任务，须综合考虑运载火箭接口、结构、电源、姿态轨道控制以及航天器总装等多个方面的工作，开展多参数、多约束的权衡优化。典型超低轨航天器由本体、翼面与对接环三部分组成，其气动构型要素分解过程如图1所示。其中：本体提供设备安装空间与太阳电池布片面积，承受主要的力学载荷。翼面包括太阳翼与稳定翼，提供太阳电池布片面积与姿态稳定能力。对接环提供运载火箭接口，尺寸与本体截面直径大小相匹配。

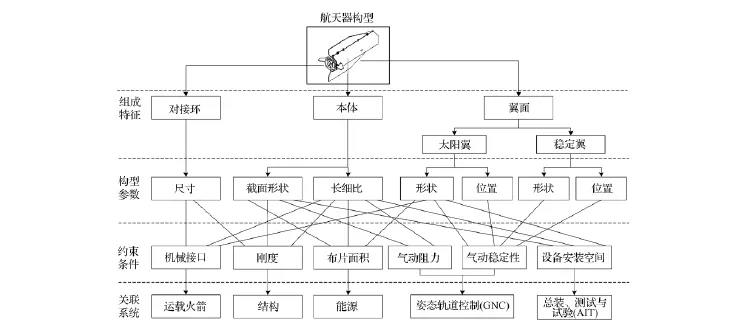
图1 超低轨航天器气动构型要素分析Fig.1 Aerodynamic configuration element analysis of ultra－LEO spacecraft

基于上述分析，气动构型关键参数包括：本体截面形状、大小以及长细比，翼面形状以及布局位置等。其中，本体截面与长细比，取决于气动阻力、干扰力矩、结构刚度等因素。从减少阻力的角度，航天器本体应选择细长构型。长细比越大，遇到的大气阻力愈小，但结构挠性增大，整体结构刚度会下降。从减少干扰力矩的角度，航天器截面形状应是面对称或者轴对称的。在相同体积的直棱柱中，圆柱体的截面最小。但考虑到设备安装与太阳电池布片需求，本体外侧面应尽量平整，因此可选择近圆的多边形截面。翼面形状取决于能源与姿态控制需求，如尽量增加太阳电池布片面积、减少姿态控制燃料消耗。从气动特性角度，可选择小展弦比的翼型，如矩形、梯形。翼面径向布局，要保证在偏航与俯仰2个方向的气动控制能力。翼面轴向布局，则要考虑静稳定要求，使质心处于压力中心的前方。这样，在姿态失稳的情况下，可以通过气动力矩提供姿态恢复力矩。增加尾翼面积或者改变轴向布置，使压力中心后移，可以提高整体的气动稳定性。

3 气动建模内容与方法

超低轨航天器的气动计算，涉及到来流气体特性、气体分子与航天器表面之间的相互作用（简称气体－表面作用）、航天器物理特性3个方面的建模内容，如图2所示。其中：来流气体特性包括分子成分、密度、速度、温度等，主要由高层大气模型来描述；气体－表面作用是指气体分子与物体壁面之间由于碰撞、反射或吸附等所产生的动量与能量交换，其模型描述的是来流气体对航天器表面单元所产生的切向力、法向力以及传热量；航天器物理特性包括外部形状、表面材料、相对运动速度、壁面温度、质量特性等信息，以有限元网格为主模型来描述。

图2 超低轨航天器气动建模内容Fig.2 Aerodynamic modeling of ultra－LEO spacecraft

3.1 来流气体特性建模

地球高层大气的密度、成分以及温度，在太阳活动周期影响下随大气膨胀、收缩而起伏。另外，大气条件在每日、季节、经度、纬度上的变化，导致了更短暂和局部的影响。这些影响可使航天器运行轨道上的来流气体特性发生数量级的变化。

高层大气模型用于描述热层的大气状态和变化过程。常用模型包括J77、CIRA1986、DTM2009、JB2008、NRLMSIS－00及MET－V2.0等，都是基于不同来源的历史数据，如加速度计、压力表、质谱仪等在轨测量结果，或者空间目标轨道特性的地基观测结果，同时假定阻力系数恒定为2.2，拟合计算得到不同高度范围的经验或半经验模型。由于受到所隐含的假设条件、太阳活动与地磁活动指数取值、历史数据来源等不确定因素的影响，大气模型的密度计算误差都在15%以上［10－11］，而且没有哪个大气模型在任何情况下都是最好的［12］。实际应用中，须要明确各种模型的假设条件与不确定因素，根据不同轨道高度、实时性要求、地磁与太阳活动情况，优选合适的大气模型。

在考虑地球自转、热层风潮的影响后，大气相对航天器的速度为

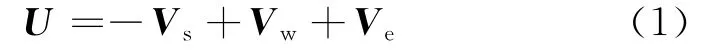
式中：Vs，Vw，Ve分别为航天器运动速度、热层风速和大气随地球自转的速度，如图3所示。

图3中，OsXYZ为航天器本体坐标系，正常飞行时X轴指向飞行方向，Z轴指向地心，Os为航天器质心；ne为地球自旋速度；i为轨道倾角；OE为地心；OEN为地球自转轴，指向北极。

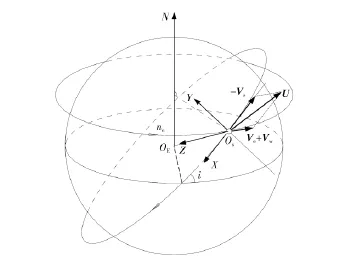
图3 来流速度Fig.3 Velocity of incident flow

航天器运动速度可以由二体问题中的活力公式得到。假设rse为航天器到地心的距离，a为轨道半长轴，μ为地球引力常数，则

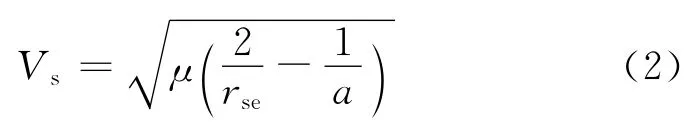
热层风的速度可达几百米每秒，对阻力加速度有较大影响。但是，由于热层的风潮变化非常复杂，尚未建立基本模式，无法给出明确的工程计算公式，只能间接地拟合观测数据得到经验模型（如HWM97），可信度较低。

目前，大气如何旋转的物理机制，还不太清楚。通常假定由于黏性作用，与地球以同一角速度旋转，即Ve＝rsecosne（为当地纬度），则Ve在航天器本体坐标系中的3个分量大小为

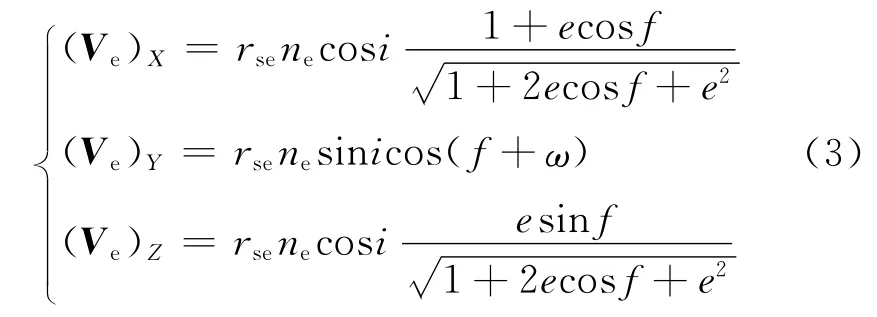
式中：e为偏心率；f为真近点角；ω为近地点幅角。

3.2 气体－表面作用建模

气体－表面作用非常复杂，涉及到量子力学方面的知识，目前还不能给出准确的理论计算公式，只能通过地基试验或在轨观测等手段获取经验模型及系数值来模拟，但仅局限于某些应用场景。近年来，一些研究尝试使用分子动力学仿真手段分析气体－表面作用的本质，并根据仿真结果，基于一些输入参数和边界条件组合使用现有的模型。这类工作在一定程度上代表了气体－表面作用建模的发展方向。当前，几个主流的经验模型是Maxwell、CLL和Nocilla［13－16］（机理如图4所示），由此产生了多个衍生模型，如Schaaf ＆Chambre模型［14］。

图4 气体－表面作用模型机理Fig.4 Mechanism of gas－surface interaction model

Maxwell模型假设反射分子流中的一部分（σ）发生漫反射，其余的（1－σ）发生镜面反射，从而将高度复杂的气体－表面作用简化表示成一些简单参数，在理论分析和实验中得到了广泛应用。Schaaf ＆Chambre模型在Maxwell模型的基础上引入了1个热调节系数（σa）和2个动量调节系数（σn，σt），分别描述气体与物面之间的能量传递、表面切向与法向的动量传递。由于上述调节系数是统计平均值，不能精确描述试验中所观测到的详细分子行为。在CLL与Nocilla模型中，假定气体没有被吸附或发生化学反应，反射流的静态温度与漂移速度是入射速度分布、动量以及壁面特征的经验函数。采用漂移的Maxwell分布函数，能够近似模拟高能分子从工程表面散射时所呈现的小叶状分布。另外，通过概率分布函数的关联，与入射流分布建立关系，因而具有速度空间连续的优势，在分子流模拟中得到了广泛应用。

根据Schaaf ＆Chambre模型，计算气体的入射流和反射流给平板物面所形成的压应力p和剪应力τ为

式中：ρ∞为大气密度；φ为U与表面法向的夹角；分子速比，T为气体热力学温度，气体通用常数R＝8.3143J／（mol·K）；Sc＝Scosφ，误差函数dt，t为积分变量；Tsw为航天器外壁面温度。

3.3 航天器物理特性建模

在自由分子流条件下，分子之间不发生碰撞，因此可以在计算中将复杂外形的航天器分解成多个简单外形的叠加，而各部分受到的气动力可独立计算，互不干扰。计算中的分解与集成过程，通常是采用有限元方法来实现的。

航天器物理特性建模思路如下［17］：首先定义航天器的本体坐标系、质量特性、质心坐标系、飞行姿态等总体信息，明确风轴坐标系、本体坐标系、质心坐标系三者之间的关系；然后利用有限元方法将航天器表面划分成多个平面单元，如三角形、四边形，建立一阶面元的网格模型，在可能发生遮挡及多次反射的地方对网格进行加密，如图5所示；最后以该网格为主模型，利用特征关联、信息附着等手段，融合航天器热分析、机构仿真以及姿态轨道控制等学科内容，给每个面元赋予相应的材料属性、表面温度、运动速度等信息，关联与单元特性相关的气体－表面作用模型与调节系数等数据。

图5 航天器表面网格模型Fig.5 Surface mesh model of spacecraft

假设航天器外表面由多个单元组成，单元j所受到的气动力Fj可由气体－表面作用模型公式计算得到。

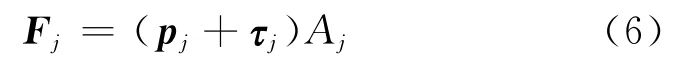
式中：pj为单元j受到的压应力；τj为单元j受到的切应力；Aj为单元j的面积。

总的气动力F和气动力矩M，可以用单元气动力Fj和单元气动力矩累加得到，即

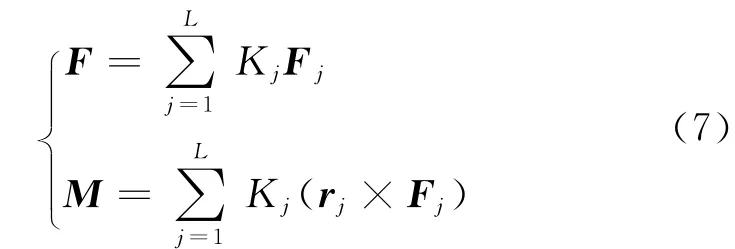
式中：Kj为单元j的遮挡因子，在来流方向上，如果表面单元j未被其他单元遮挡，Kj取值为1，否则取值为0；rj为单元j的气动力等效作用点（即压心）到航天器质心之间的矢径；L为单元数量。

4 自由分子流模拟方法

目前，主要有4种方法来模拟自由分子流的运动与作用过程［18］，包括平板（Panel）方法、射线跟踪平板法（Ray－Tracing Panel，RTP）、直接仿真蒙特卡洛（Direct Simulation Monte Carlo，DSMC）方法、试验粒子蒙特卡洛（Test－Particle Monte Carlo，TPMC）方法。其中：Panel方法只适用于简单凸形体，没有考虑遮挡与多次反射。RTP方法在平板方法的基础上，引入了射线跟踪算法，解决了几何表面相互遮挡问题。DSMC方法作为一种典型的分子运动模拟方法，虽然能够计算粒子之间以及粒子与表面之间的动量与能量交换，但很少应用于自由分子流领域的分析工作。这是因为自由流分子之间极少发生碰撞，而使用无碰撞的DSMC方法并不能提供比平板法或其他方法更高的精度，却要求使用者具备稀薄气体动力学方面的专业知识，并且花费更多的计算时间。因此，DSMC方法常用于过渡流领域的气动分析。TPMC方法采用随机模拟法模拟大气分子运动，不考虑分子间碰撞，计算量正比于仿真分子数量，比RTP方法慢得多，但可处理超热及亚超热自由流中复杂形体的局部凹陷区域问题。

TPMC方法的基本思路如图6所示［9］：首先构建一个计算域，并在边界产生一个试验粒子；然后跟踪和模拟该粒子的运动轨迹和碰撞过程，直到飞出计算域或撞到航天器表面，若试验粒子和表面碰撞，计算其与航天器表面的动量、能量交换；重复上述过程，直至试验粒子数足够大，以保证结果收敛；最后统计得到航天器整体力、热等参数。图6中，计算域为一个圆柱体，包括前面f、后面b、侧面s共3个边界区域。试验粒子的初始位置与初始速度，按照概率分布随机取样确定。试验粒子从计算域边界逐个入射后，可以在航天器表面上多次反射，但不与其他粒子相互作用。

图6 试验粒子蒙特卡罗方法示意Fig.6 Schematic of TPMC method

对于定常扰流问题，来流的速度分布函数是平衡态的分布。假设圆柱体计算域的半径为Rc、长度为Lc，采用柱坐标系（r，θ，l）表示其边界，根据Maxwell速度分布函数，可以算出前面f、侧面s、后面b的分子数通量如下。

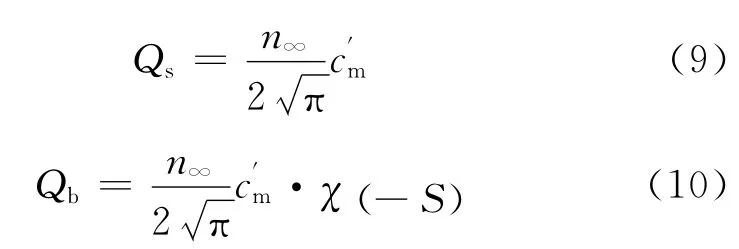
式中：n∞为自由来流分子数密度；最可几分子热运动速度；函数χ（S）定义见式（11）。

假设计算域前面f、侧面s、后面h的面积分别为Af，As，Ab，则试验粒子在计算域各表面产生的概率为

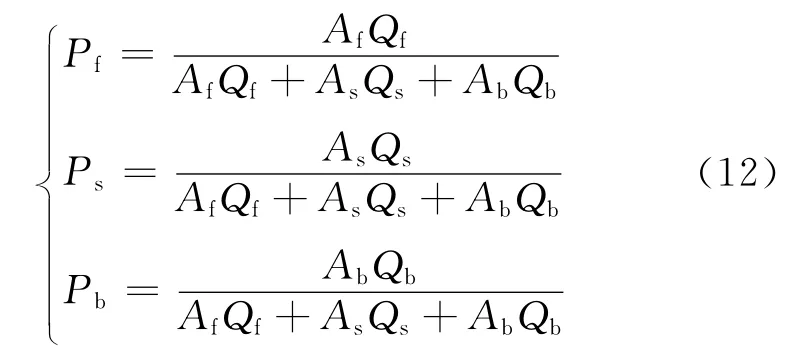
假设试验粒子在每个表面内均匀随机分布，R1，R2为随机数，θ1＝2πR2，则计算域前面f、后面b的试验粒子相对本体坐标下的初始位置（xf，b，yf，b，zf，b）取样为

计算域侧面s的初始位置（xs，ys，zs）取样为

试验粒子的初始速度c为来流速度c0与热运动速度c′之和。无量纲形式的热运动速度在柱坐标系（r，θ，l）中的分量为（ξr，θr，ξl），边际概率分布密度为

式中：θc为面单元与来流速度c0之间的夹角；R3，R4，R5为随机数。

利用概率分布函数求逆、多项式拟合得到

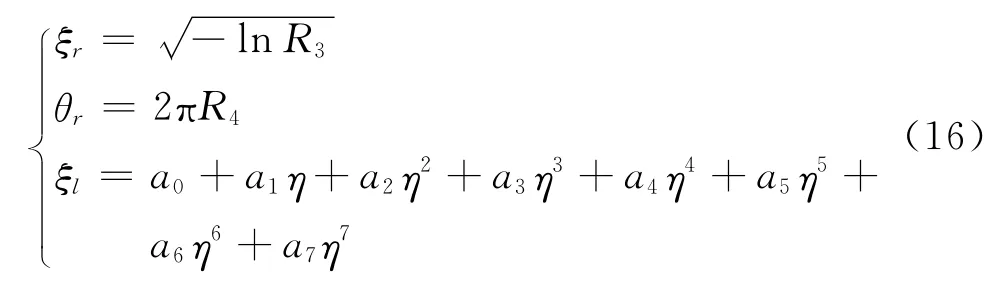
式中：a0～a7为多项式系数；

5 气动计算及仿真流程

基于上述建模思路以及自由分子流模拟方法，本文提出了一种综合TPMC与RTP的航天器气动计算流程，如图7所示。该流程利用TPMC方法确定入射粒子的初始位置与速度，采用RTP方法解决表面单元之间的遮挡问题，通过概率取样模拟粒子在表面的多次碰撞过程，可以解决复杂形体凹陷区域周围的分子入射问题，同时可以简化计算量，提高计算速度，因此不需要大型计算平台，在普通计算机上就可以完成日常的工程计算与联合仿真工作。

图7 在轨航天器气动计算流程Fig.7 Aerodynamic calculation process of spacecraft on orbit

另外，本文提出的流程还采用了有限元分解与集成方法。计算时，要先分析各单元之间的遮挡情况，在单元局部坐标系下计算各单元所受到的切向力与法向力，然后在航天器坐标系下综合得到整体的气动力与气动力矩。由于粒子入射速度综合了分子热运动、大气随地球自旋、热层风速，以及航天器轨道、姿态及部件运动等多个要素，因此该流程能够支持低分子速比的自由分子流计算、自旋卫星的气动阻尼计算等任务。

计算过程包括：航天器建模、轨道、姿态及环境参数设置、入射流特性计算、入射粒子取样、单元遮挡分析、单元气动力计算、反射流运动模拟、总体气动力与气动力矩统计、对轨道与姿态的影响分析等环节。其中：反射流运动模拟，为一个子循环，模拟分子发生多次碰撞的情况，碰撞次数设定统一的上限值。入射粒子取样采用TPMC方法，取样次数在计算前统一确定。单元遮挡分析采用RTP方法，射线矢量由入射粒子的初始位置与速度方向确定。计算中，针对每个试验粒子，分配一个独立线程，并行计算不同粒子所产生的作用力。分析过程随着轨道飞行时间而不断推进，而且在每一时间步中融入轨道、姿态、空间环境等方面的更新信息。

6 实例验证

重力梯度测量卫星通过轨道运动来反演地球重力场模型，因此对气动干扰等环境因素的计算精度要求极高。由于轨道高度为250km左右，低于载人飞船、空间站的轨道，减阻设计及气动稳定性主宰了卫星构型，也间接确定了无拖曳控制方案的输入。以这类卫星为背景，本文开展了气动构型、建模、分析以及优化等研究，初步验证所提出的设计思路、建模方法以及计算流程的合理性。

首先，针对星体截面与长细比，开展多方案权衡研究。截面方案，包括正八边形、正六边形、不等边六边形、正四边形4种形状。截面直径与长细比的权衡，如图8所示，判断依据包括结构刚度与阻力系数。分析中，借鉴了GOCE卫星结构形式与质量特性等数据，并假定在体积不变的前提下改变星体截面直径或者长细比，计算得到整星的结构基频与阻力系数。可以看出：对于中间加层板的承力筒结构，截面直径为1010mm时，星体横向基频达到最大，长细比超过4.9的拐点后，横向基频迅速降低。长细比在23左右时，阻力系数最小。

图8 截面直径与长细比的权衡曲线Fig.8 Tradeoff between cross－sectional diameter and slenderness ratio

翼面形状与布局的权衡方案，如图9所示。考虑到太阳同步晨昏轨道的供电需求，卫星采用垂直太阳翼和水平稳定翼的十字型布局。其中：太阳翼为满足布片要求，面积较大。稳定翼只考虑扰动力矩控制要求，面积很小。为避免机构微振动对有效载荷测量产生影响，翼面与星体之间采用固定式连接。为保证视场等要求，推力部件、天线、姿态控制敏感器等星外设备，布设在翼面边缘上。翼面的轴向布局位置比较靠后，以保证飞行姿态自动恢复能力，减少主动姿态控制次数及燃料消耗。

气动建模与计算方法的验证工作，涵盖了不同的大气模型、不同的物面反射模型以及分子流模拟方法。研究表明：实际的工程计算中存在很多不确定性因素，如来流大气密度、气体表面作用调节系数、表面网格质量、试验粒子数量等，对计算结果可能造成30%以上的误差影响；当TPMC方法试验粒子总数为1×107时，相对统计误差为1×10－3，单次计算时间约为200s，与DSMC方法相比，计算时间降低3～4个数量级，相同输入下的计算结果基本吻合。测试验证算例采用GOCE卫星，主要参数和典型飞行条件取自文献［19］，考虑了完全漫反射（σ＝1）和部分漫反射（σ＝0.6）2种情况，计算结果与文献［19］的对比见图10。可以看出：随着分子速比的增加（可以理解为飞行速度大小的增加），阻力系数呈指数型减小；分子速比较小时，完全漫反射对应的阻力系数大于部分漫反射的，分子速比较大时则刚好相反。2种情况下，计算结果和文献［19］结果都符合得很好，相对误差均在2%以内，验证了计算方法的正确性和程序的可靠性。

图9 翼面形状与布局方案Fig.9 Shapes and layout of wing

图10 GOCE卫星的阻力系数计算结果与文献［19］结果的对比Fig.10 Comparison of drag coefficient between calculation results and literature［19］results for GOCE satellite

7 结束语

本文系统地介绍了超低轨航天器气动研究所涉及的相关内容，并基于工程实用、准确、快捷的目标，提出了气动外形设计的影响因素与气动力、气动力矩的计算方法。其中的气动构型准则，适用于所有以减阻、增稳为目标的低轨航天器，具有普遍的参考价值。所提出的工程计算方法与流程，可有效降低气动计算量以及资源消耗，满足近实时、多学科联合仿真需求，支持普通计算机软件开发。由于已有工作着重于方法探讨，因此在不确定因素控制、集成建模与结果处理、联合仿真接口等方面，还有待于进一步研究。

（References）

［1］沈青.稀薄气体动力学［M］.北京：国防工业出版社，2003 Shen Qing.Rarefied gas dynamics［M］.Beijing：National Defense Industry Press，2003（in Chinese）

［2］黄志澄.航天空气动力学［M］.北京：中国宇航出版社，2005 Huang Zhicheng.Aerospace aerodynamics［M］.Beijing：China Astronautics Press，2005（in Chinese）

［3］Klinkrad H，Koppenwallner G，Johannsmeier D，et al.Free－molecular and transitional aerodynamics of spacecraft［J］.Advances in Space Research，1995，16（12）：33－36

［4］Enrico Canuto.Drag－free and attitude control for the GOCE satellite［J］.Automatica，2008，44（7）：1766－1780

［5］Daniel D Mazanek，Renjith R Kumar，Hans Seywald，et al.GRACE mission design：impact of uncertainties in disturbance environment and satellite force models，Paper AAS 00－163［R］.San Diego：AAS，2000

［6］陈明.超低轨道卫星气动力辅助轨道保持的应用研究［D］.哈尔滨：哈尔滨工业大学，2010 Chen Ming.Application of aero－assisted orbital maintenance to ultra－low－orbit satellite［D］.Harbin：Harbin Institute of Technology，2010（in Chinese）

［7］刘巧林.超低轨道航天器姿态控制方法研究［D］.长沙：国防科技大学：2010 Liu Qiaolin.Attitude control method of ultra－low－orbit spacecraft［D］.Changsha：National University of Defense Technology，2010（in Chinese）

［8］周伟勇，张育林，刘昆.超低轨航天器气动力分析与减阻设计［J］.宇航学报，2010，31（2）：342－347 Zhou Weiyong，Zhang Yulin，Liu Kun.Aerodynamics analysis and reduced drag design for the lower LEO spacecraft［J］.Journal of Astronautics，2010，31（2）：342－347（in Chinese）

［9］靳旭红.自由分子流的试验粒子Monte Carlo方法［D］.北京：中国航天空气动力技术研究院，2015 Jin Xuhong.The test particle Monte Carlo method for free molecular flows［D］.Beijing：China Academy of Aerospace Aerodynamics，2015（in Chinese）

［10］David A Vallado，David Finkleman.A critical assessment of satellite drag and atmospheric density modeling［C］／／Proceedings of AIAA／AAS Astrodynamics Specialist Conference and Exhibit，2008.Washington D.C.：AIAA，2008：141－165

［11］Frank A Marcos，John O Wise，Michael J Kendra，et al.Satellite drag research：past，present and future［C］／／Proceedings of AIAA／AAS Astrodynamics Specialist Conference and Exhibit，2003.Washington D.C.：AIAA，2003：1865－1878

［12］苗娟，刘四清，李志涛，等.热层大气密度变化特征与太阳辐射和地磁指数的相关性分析［J］.载人航天，2012，18（5）：24－30 Miao Juan，Liu Siqing，Li Zhitao，et al.Correlation of thermosphere density variation with different solar and geomagnetic indices［J］.Manned Spaceflight，2012，18（5）：24－30（in Chinese）

［13］Gaposchkin E M.Calculation of satellite drag coefficients［R］.Lexington：MIT Lincoln Lab，1994

［14］Schaaf S A，ChambréP L.Flow of rarefied gases，fundamentals of gas dynamics［M］.Princeton：Princeton University Press，1958：687－708

［15］Woronowicz M S，Rault D F G.Cercignani－Lampis－Lord gas－surface interaction model：comparisons between theory and simulation［J］.Journal of Spacecraft and Rockets，1994，31（3）：532－534

［16］Frank G Collins，E C Knox.Parameters of Nocilla gassurface interaction model from measured accommodation coefficients［J］.AIAA Journal，1994，32（4）：765－773

［17］胡凌云，丁延卫，张立华.低轨卫星气动力及气动力矩精确计算模型［C］／／2011航天与力学高峰论坛论文集.北京：北京空间飞行器总体设计部，2011：126－134 Hu Lingyun，Ding Yanwei，Zhang Lihua.Precise model of aerodynamic force and aerodynamic torques for LEO satellites［C］／／Proceedings of 2011Spaceflight and Mechanics Forum.Beijing：Beijing Institute of Spacecraft System Engineering，2011：126－134（in Chinese）

［18］Benjamin P Graziano.Computational modeling of aerodynamic disturbances on spacecraft within a concurrent engineering framework［D］.London：Cranfield University，2007

［19］Koppenwallner Georg.Satellite aerodynamics and determination of thermospheric density and wind［C］／／Proceedings of the 27th International Symposium on Rarefied Gas Dynamics.College Park，NY，American Institute of Physics（AIP），2011：1307－1312

（编辑：夏光）

Method of Aerodynamic Design and Calculation for Ultra－LEO Spacecraft

HU Lingyun1ZHANG Lihua1CHENG Xiaoli2JIN Xuhong2DING Yanwei1
（1DFH Satellite Co.，Ltd.，Beijing 100094，China）（2China Academy of Aerospace Aerodynamics，Beijing 100074，China）

Aerodynamic force is the major disturbance to orbit for ultra－LEO spacecraft at 150～300km altitude.The design principles for configuration of ultra－LEO spacecraft is introduced firstly，including shape of body，slenderness ratio，shape of wings and layout of wings.The approaches to accurate aerodynamic modeling are illustrated in terms of properties of incident flow，gas－surface interaction and physics of spacecraft.The process for engineering calculation and flight simulation is proposed，which incorporates two methods including RTP（ray－tracing panel）and TPMC（test－particle Monte Carlo）.Some aerodynamic researches on a satellite for measuring gravity gradient are conducted，and the method of modeling and the process of computation are validated.The approaches presented in this paper can be applied to aerodynamic design and calculation of ultra－LEO spacecraft.

ultra－LEO spacecraft；aerodynamic design；aerodynamic modeling；aerodynamic analysis；satellite for measuring gravity gradient

V211.25

：ADOI：10.3969／j.issn.1673－8748.2016.01.002

2015－06－05；

：2015－10－08

胡凌云，男，高级工程师，从事小卫星机械总体设计及在轨组装与在轨服务研究工作。Email：hulingyun＠cast.cn。