卫星编队连续推力控制的燃料平衡方法

段晨阳 赵亚飞 张世杰 孔宪仁

（哈尔滨工业大学卫星技术研究所，哈尔滨 150080）

卫星编队连续推力控制的燃料平衡方法

段晨阳 赵亚飞 张世杰 孔宪仁

（哈尔滨工业大学卫星技术研究所，哈尔滨 150080）

在卫星编队飞行中，编队重构等机动过程会导致整个编队卫星之间燃料消耗不均匀，甚至出现某一成员卫星燃料消耗完，而导致整个编队构型提前结束乃至任务失败。针对该问题，文章提出了在卫星编队轨道重构过程中可采用的一种燃料平衡方法，即基于连续推力控制，以燃料最优为控制目标，通过建立燃料消耗函数，推导了不同相位角及重构半径时的最优控制加速度，通过减小各从星之间的燃料消耗函数的差异，使得不同成员卫星燃料消耗差别最小。编队卫星燃料平衡程度取决于初始相位角，文章给出了最佳初始相位角的表达式。最后，对以一主二从的三星编队在从星轨道重构中的从星燃料平衡问题进行了仿真，分别验证了卫星编队连续推力控制方法和编队卫星燃料平衡方法的正确性和有效性。

卫星编队；轨道重构；燃料平衡；连续推力

1 引言

卫星编队飞行是人类对天空探索及实现卫星协同工作的重要技术。通过编队飞行，可实现干涉测量［12］、立体成像［3－4］、空间监测等多种任务。通过卫星间的协调工作，可实现单星无法完成的任务，对未来宇宙探索和空间服务具有重要意义。随着卫星推进技术的发展，卫星推进方式实现了从化学推进—化学／电推进—电推进的过渡，在未来编队飞行任务中，电推进等新型推进技术有助于减少卫星对燃料的依赖，具有广阔的发展前景。在ESA发布的下一代卫星平台（Next－generation Satellite Platform）研究中，电推进方式以其高效节能的特点被列为重点发展目标之一。

编队飞行中各成员卫星之间协同工作，在轨以某种构型存在，实现任务的需求和功能。编队飞行与单星飞行相比，可实现的功能更为复杂。但是，编队飞行也有其自身的缺点，如轨道机动导致卫星之间燃料消耗不一致，最终可能使得某一成员卫星燃料耗尽，进而导致编队性能降低，构型提前结束，甚至无法完成预期的在轨任务。美国、俄罗斯等国家已经开始了对编队卫星重构中的燃料平衡问题的研究［5］。一些学者提出在工程上采用控制分配方法，约束轨道重构中成员卫星之间的燃料消耗［6－8］。Susan A.Frost将燃料平衡指标转化为范数最优问题，达到了均衡燃料消耗的目的［9－10］。在重力场和深空环境两种约束下，Amirreza R.等对双星和三星编队机动中的燃料平衡问题进行了仿真验证［11］。Beard R.W.等开展了相关的工作，为燃料平衡问题的研究提供了一定的理论依据［12］。

本文对采用连续推力轨道控制模式下的编队重构的燃料平衡问题进行研究，给出了响应的理论和方法，可供未来编队卫星的燃料平衡控制参考。

2 编队燃料平衡优化设计

在确定燃料平衡问题模型之前，首先须要定义卫星编队重构中采用的坐标系，并介绍卫星编队重构的基本原理。在此基础上，逐步分析编队燃料平衡优化设计中涉及到的关键技术。

2.1 坐标系定义

本节主要介绍本文涉及的两种坐标系：惯性坐标系和轨道坐标系，如图1所示。

（1）惯性坐标系：原点O位于地心，OX轴指向春分点方向，OZ轴垂直于赤道面，并指向北极方向，OY轴与OX和OZ轴成右手系。

（2）轨道坐标系：原点o位于主星质心，ox轴由地心指向卫星方向，oz轴垂直于轨道面，并指向轨道角动量方向，oy轴和ox、oz轴构成右手系。

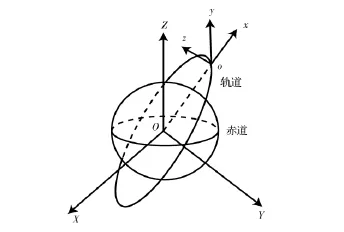
图1 坐标系Fig.1 Coordinate frame

2.2 卫星编队重构可行性分析

假设编队卫星主星在圆轨道上运行，在主星轨道坐标系下，各颗从星其相对于主星的位置变化规律可用CW方程表述。令x，y，z为主星轨道坐标系的坐标分量，为主星轨道坐标系内表达的速度分量。考虑进行连续推力轨道控制，令三个方向的控制加速度分别用Tx，Ty，Tz表示，它们可以是关于时间的函数，则相应的运动方程可以写成

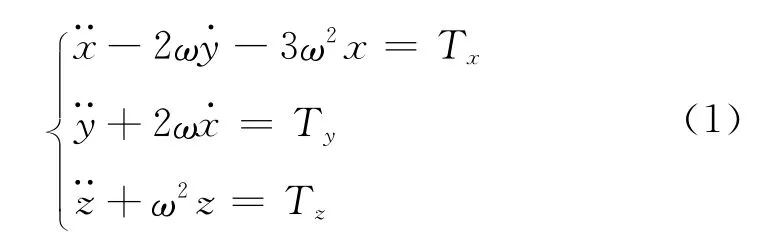
式中：ω为轨道坐标系相对惯性坐标系的转动角速度。

在卫星编队飞行重构的过程中，总的燃料消耗可以表示为各个方向控制加速度的函数，假设编号为i的编队成员卫星初始相对运动状态和期望相对运动状态分别表述为ri0，rif，那么在编队重构过程中，燃料消耗表示为两个状态量的函数。在满足编队飞行总体构型性能的前提下，根据每一个编队成员初始状态，合理确定其期望状态，以达到每颗卫星的剩余燃料差别最小，实现燃料平衡的目的。

2.3 核心技术分析

1）连续推力模型

在对编队重构中的推力器工作情况未知的情况下，可以将Tx，Ty，Tz写成关于时间的任意连续函数，本文将其写成傅里叶函数形式［13］：

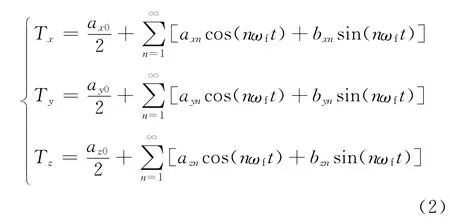
式中：ax0，ay0，az0，bxn，byn，bzn为常值量；ωf＝2π／tf。为了简化运算，只取前5项的表达式作为加速度的表达形式。

2）编队重构定义

编队重构涉及到两个方面：x－y轨道平面内机动和轨道面外机动。给定轨道机动时间tf，通过连续推力控制，卫星从初始位置和速度，到达目标状态。在主星轨道坐标系下，o点与从星在y－z平面的投影位置的连线，按逆时针方向与z轴的夹角α称为相位角。在主星轨道周期内，从星在y－z平面投影位置与主星位置连线扫过的圆的半径定义为投影圆半径。图2给出了投影圆编队卫星的相位角关系。

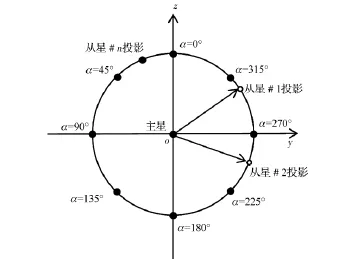
图2 相位角Fig.2 Phase angle

卫星重构包含以下两个方面的内容：①从初始编队投影圆半径R，经过轨道重构后，编队重构后新的投影圆半径为R＋ΔR；②从初始相位角α，经过轨道重构后，相位角变为α＋Δα。

3）最优控制技术

最优控制方法从每个从星的轨道重构出发，分别建立各自的燃料目标函数，通过对每个从星燃料消耗的合理调度，达到机动后编队卫星之间彼此燃料平衡的要求，并限制总燃料消耗，从而在完成卫星编队燃料平衡问题的同时，使得编队重构总燃料消耗最优。

3 编队卫星重构方法

3.1 编队卫星重构问题研究

在连续推力假设下，相对轨道面外和轨道面内的燃料目标函数可以写成

对每一个编队成员卫星，在编队重构过程中，最优控制可以写成（相关推导见参考文献［13］）

式中：T0，T1，λ0，λ1是从星初始相位角、投影圆半径及其变化函数；Λ，Φ，ζ为推导过程中产生的中间变量（见参考文献［13］）。

根据z方向和x－y方向的燃料消耗最优目标函数，经过优化目标函数J＝Jxy＋Jz，可以得到最优相位角α＊的两个解：

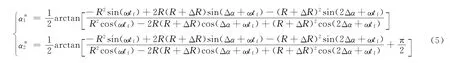
根据取得极小值条件，验证哪一个是取得极小值的最优相位角。这也证实了在这种机动策略下，总的燃料消耗仅仅取决于从星在主星轨道坐标系的相位角初值，因此通过选择合理的从星初始相位角，可以达到节省燃料的目的。

3.2 实例验证

假设主星运行在高度为1000km圆轨道，初始编队投影圆半径为30km，轨道重构后的轨道半径为50km，相位角变化30°，转移时间1600s。根据式（5）的结论，可以得到α＊＝72.352 6°时燃料最省。一般来说，使得燃料平衡的解并不是唯一的，总是趋向于选取燃料消耗最小的那一组解作为最优解。

图3给出了编队轨道重构过程中的相对轨道变化情况，细圆圈“o”表示无控情况下，从星经过时间tf之后的位置，黑线表示在主星轨道坐标系下的从星相对转移轨道。从图3中可以看出，从星从初始相对轨道半径为30km的投影圆轨道出发，经过转移时间tf，重构后的相对轨道半径为50km，能够完成轨道半径变化的要求。在轨道重构过程中，完成轨道重构需要的速度增量为0.056 8km／s。

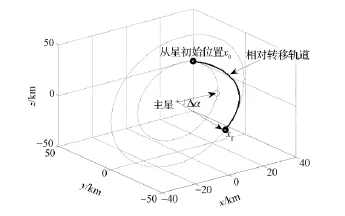
图3 主星轨道坐标系下的轨道重构Fig.3 Orbital reconfiguration described in orbital frame of chief satellite

假设从星自初始相对位置经过，自由飞行时间tf后的相对位置为（yf0，zf0），采用连续推力飞行时间tf后的位置为（yf，zf），则有

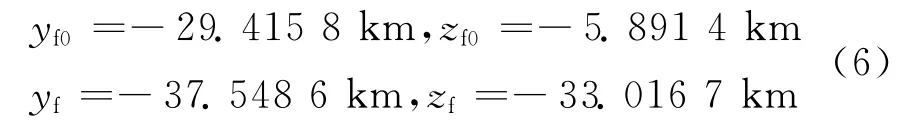
相应地，y－z平面投影圆相位角的变化为

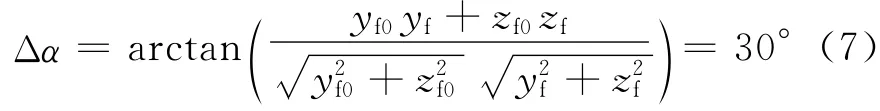
这与期望的相位变化角一致，在完成对相对轨道半径大小控制的同时完成了相位角变化机动。

图4给出了轨道转移过程中的燃料消耗随初始相位角变化的情况，从图4中可以看出，燃料消耗变化的周期是180°，使得燃料消耗最少的初始相位角为αmin＝72.352 6°，这和计算得到的结果是一致的，从而证实了上述原理的正确性。由于解的周期性，可见只要相位角的最优解并不是唯一的，这里只给出了0～180°的结果。

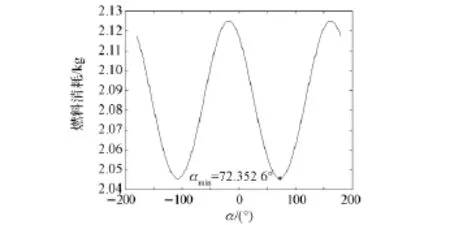
图4 燃料消耗－初始相位角变化曲线Fig.4 Variation of fuel consumption as a function of initial phase angle

4 编队燃料平衡方法

两个从星的轨道重构所对应的三星燃料平衡问题。假设两颗从星的初始质量和携带燃料的状况相同，那么一个简单的想法是在同等的转移条件下（转移时间，起始时间等），使得两颗星的燃料消耗相等，并且能够完成相应的轨道重构半径和相位角的改变。

4.1 三星燃料平衡问题

本节讨论的三星燃料平衡问题，是指在主从式卫星编队中，从星＃1和从星＃2同一时间从不同的初始位置进行轨道机动，达到一个新的编队构型。经过这样的轨道重构后，从星＃1和从星＃2相对主星不仅相对距离发生变化，而且在主星轨道坐标系下，其相位角也发生改变，相位角的改变量分别用Δα1，Δα2表示，如图5所示。对于具有两颗从星的编队卫星重构问题，如果其初始燃料相同，并且在轨道重构过程各颗从星之间彼此燃料消耗差别最小，则满足编队燃料平衡的需求，其流程如图6所示。

引入如下中间变量

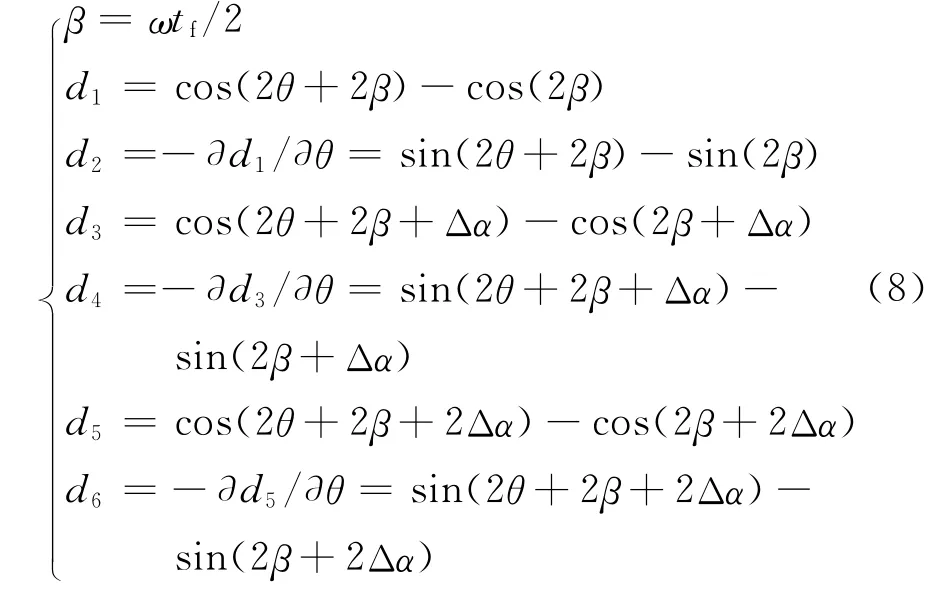
式中：ω为轨道坐标系相对惯性坐标系的角速度；θ为从星间的初始相位差；Δα为从星相位变化量。

假设两颗星初始相位角差θ已知，因此，只要能够求得其中一颗星的初始相位角，就可以确定另一颗卫星的初始相位角，经过理论推导和构建燃料平衡的目标函数，满足燃料平衡时，相位角须满足：

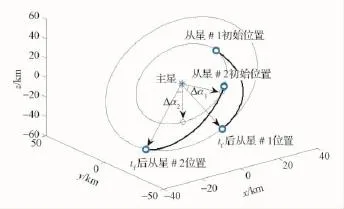
图5 轨道重构示意图Fig.5 Depiction of orbital reconfiguration

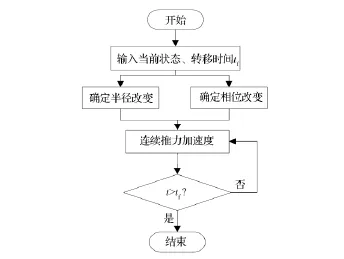
图6 编队重构燃料平衡方法流程Fig.6 Flow chart of balancing formation reconfiguration

4.2 实例仿真

假设主星在轨道高度为1000km的圆轨道上运行，在主星轨道坐标系下，两颗从星在y－z平面半径为30km的投影圆轨道上运行，初始相位角相差60°。在t0时刻，两颗从星开始机动，经过时间tf，两颗从星到达新的投影圆相对运行轨道，新的轨道y－z平面轨道半径为50km，假设两颗从星相位角变化相同，即Δα1＝Δα2＝30°，对4.1节中提出的燃料平衡算法进行仿真验证。

基于上述假设，从星＃2的初始相位角与从星＃1的初始相位角之间恒定差一个角度θ，因此，两颗从星的燃料消耗都可以看作从星＃1初始相位角的函数，如图7所示，实线表示从星＃1的燃料消耗－初始相位角变化曲线，虚线表示从星＃2的燃料消耗－从星＃1初始相位角变化曲线。可以证明，燃料－相位角变化曲线的周期为180°，因此，我们这里只关注初始相位角在－90°≤α0≤90°范围内的结果，从图7中可以看出，两条曲线共有两个交点，分别为，并且在从星＃1的初始相位角时，达到燃料平衡，并且燃料消耗最优。在轨道重构过程中，完成轨道重构需要的速度增量为0.064 8km／s。

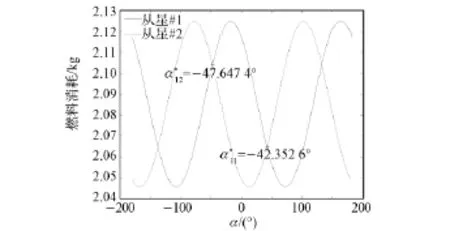
图7 两颗从星的燃料消耗随从星＃1初始相位角变化曲线Fig.7 Variations of fuel consumptions of two deputy satellites with different initial phase angles of deputy＃1

通过施加连续推力，从星＃1和从星＃2从初始位置出发，进入转移轨道，脱离原来半径为30km的投影圆轨道，经过设定的轨道重构时间tf，同时到达预定的半径为50km的投影圆轨道，整个过程在y－z平面的投影如图8所示，其中粗线圈表示从星＃1和＃2在t0时刻的位置以及在t0＋tf时刻的位置，从图8中可以看出采用4.1节给出的方法能够完成轨道重构，满足相对轨道半径变化的要求。与此同时，轨道重构另一个目标要求是完成相位角的改变，初始时刻两颗星的相位角差为θ＝60°。对于从星＃1，机动前后的相位变化角为Δα，同样地，对于从星＃2有一样的结论，经计算，Δα＝30°，这与任务要求的两颗星相位角变化30°的要求是一致的。因此，此方法既可以完成相对轨道位置的变化，又可以完成相位角变化的要求，从而证明了该方法的有效性。

图9给出了3个主星轨道坐标系下三个坐标轴方向的变化曲线，从推力函数的构造不难看出，推力函数是有三角函数构成的初等函数，因此表现为不同峰值、不同频率的周期变化曲线的叠加形式，与PD控制率等不同，其连续变化曲线在逐渐接近目标位置时，并不表现为逐渐趋近于0，因此，在本文的理论框架下，在设定好转移时间后，须要主动关闭发动机。

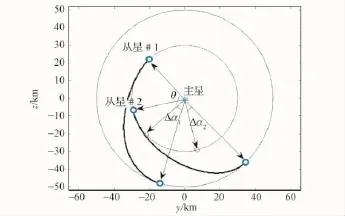
图8 y－z平面投影圆相位角变化图Fig.8 An increment in phase angle illustrated in projected circle in y－z plane

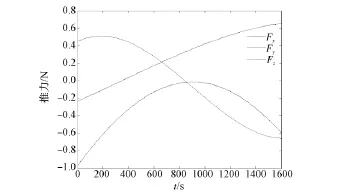
图9 从星＃2推力变化情况Fig.9 Working status of thrusts of deputy＃2

5 结论

本文对卫星编队重构过程的燃料平衡问题进行了研究，在给定初始轨道情况及目标轨道参数的情况下，给出了卫星编队重构方法，在此基础上，对编队重构中的燃料平衡问题进行了研究。经研究，得出了以下结论：

（1）在给定初始编队状态和目标编队状态的情况下，可以通过连续推力控制实现轨道重构。本文给出了编队重构方法，并对其有效性进行了仿真验证。

（2）在初始燃料相同的情况下，研究了双从星编队重构的燃料平衡问题，通过构造燃料目标函数，给出了求解最优初始相位角的求解方法，在设定相对运动轨道半径和相位角变化的情况下，实例仿真证明该方法能够有效地完成机动过程，并达到燃料平衡。

（References）

［1］郝继刚，张育林.SAR干涉测高分布式小卫星编队构型优化设计［J］.宇航学报，2006，27（4）：654－669 Hao Jigang，Zhang Yulin.Formation optimized design for the height measurement of InSAR using distributed micro－satellites［J］.Journal of Astronautics，2006，27（4）：654－669（in Chinese）

［2］Alberto Moreira，Gerhard Krieger.Spaceborne synthetic aperture radar（SAR）systems：state of the art and future developments［C］／／11thGAAS Symposium.Munich：Global Automotive Aftermarket Symposium，2003：385－388

［3］Jianying Wang，Zhaowei Sun.6－DOF robust adaptive terminal sliding mode control for spacecraft formation flying［J］.Acta Astronautica，2012，73：76－87

［4］Wu Y H，Cao X B，Xing Y J，et al.Relative motion coupled control for formation flying spacecraft via convex optimization［J］.Aerospace Science and Technology，2010，14（6）：415－428

［5］Sung Moon Yoo，Sang Young Park，Kyu Hong Choi.A fuel balancing method for reconfiguration of satellite formation flying［C］／／International Conference on Control，Automation and Systems.Seoul：International Mechanical and Mechatronics Engineering Committee，2007：1426－1429

［6］W C Durham.Constrained control allocation［J］.Journal of Guidance，Control，and Dynamics，1993，16（4）：717－725

［7］Johansen T A，Fossen T I.Control allocation—a survey［J］.Automatica，2013，49（5）：1087－1103

［8］Shengyong T，Zhang S，Zhang Y.A modified direct allocation algorithm with application to redundant actuators［J］.Chinese Journal of Aeronautics，2011，24（3）：299－308

［9］Susan A Frost，Marc Bodson.Resource balancing control allocation［C］／／American Control Conference，Washington D.C.：AIAA，2010：1326－1331

［10］Bodson M，Frost S A.Load balancing in control allocation［J］.Journal of Guidance，Control，and Dynamics，2011，34（2）：380－387

［11］Rahmani A，Mesbahi M，Hadaegh F Y.Optimal balancedenergy formation flying maneuvers［J］.Journal of guidance，control，and dynamics，2006，29（6）：1395－1403

［12］Beard R W，McLain T W，Hadaegh F Y.Fuel optimization for constrained rotation of spacecraft formations［J］.Journal of Guidance，Control，and Dynamics，2000，23（2）：339－346

［13］P Palmer.Optimal relocation of satellites flying in nearcircular－orbit formations［J］.Journal of Guidance，Control，and Dynamics，2006，29（3）：519－526

（编辑：张小琳）

Fuel－balancing Using Continuous Thrust in Satellite Formation Flying

DUAN Chenyang ZHAO Yafei ZHANG Shijie KONG Xianren
（Research Center of Satellite Technology，Harbin Institute of Technology，Harbin 150080，China）

In satellite formation flying，maneuvering such as formation reconfiguration would cause unbalanced fuel distribution among the formation satellites.It may be worse if one of the satellites fails，which leads to a short lifetime formation，or complete loss of its basic function.Aiming at the problem the paper proposes a fuel－balance approach using continuous thrust，which can be adopted during orbital reconfiguration of satellite formation.The approach uses continuous thrust，brings up a fuel－consumption objective function，and derives different optimal control acceleration with different phase angles and radius changes.We reduce the fuel difference in the formation by minimizing the difference of fuel－consumption functions between each two satellites.Fuel－balancing depends on the different initial phase angle.This paper gives a expression of initial phase angle.Eventually，we use a formation of three satellites in simulation，the simulation proves the proposed methods，continuous thrust control and fuel－balancing method are valid and effective.

satellite formation；orbit reconfiguration；fuel－balance；continuous thrust

V474.3

：ADOI：10.3969／j.issn.1673－8748.2016.01.003

2015－11－19；

：2016－01－09

国家自然科学基金（91438202），民用航天“十二五”预研项目

段晨阳，男，博士研究生，研究方向为航天器动力学与控制。Email：hitsat＠gmail.com。