点式连接航天器等效刚度模态分析方法

石川千周徐斌张永涛，2杜冬李昊

（1上海卫星工程研究所，上海 200240）

（2上海利正卫星应用技术有限公司，上海 200240）

点式连接航天器等效刚度模态分析方法

石川千1周徐斌1张永涛1，2杜冬1李昊1

（1上海卫星工程研究所，上海 200240）

（2上海利正卫星应用技术有限公司，上海 200240）

针对点式连接航天器受接触影响而产生的非线性特性，提出了利用线性等效刚度代替非线性刚度以计算点式连接航天器模态的分析方法。首先采用有限元软件对点式连接航天器的非线性刚度进行分析，并基于非线性振动和结构动力学的原理，建立了等效刚度的计算方法。将等效刚度代入广义弹簧单元，最终获得点式连接航天器的简化模型并分析其模态。模态分析结果与试验结果对比显示，相比于传统分析方法，基于等效刚度的简化模型精确地预测了点式连接航天器的模态，有利于提高点式连接航天器的动力学仿真分析精度。

航天器；点式连接；模态；等效刚度；非线性特性

1 引言

随着航天技术应用时代和外层空间实用时代的到来，结构大型化、复杂化和模块化已成为航天器的一个发展趋势［1］，点式连接多被应用在航天器本体和部件之间、舱段之间、航天器与运载火箭之间以及航天器之间。在保证强度和刚度的要求下，点式连接的螺栓数量（4～12个）一般少于普通舱段连接的螺栓数量（48～64个，参见国内外典型卫星平台），而且点式连接结构简单轻便，满足了航天器轻量化的指标要求，并具有可靠性高、承载能力强的特点。例如某大型高轨卫星舱段间连接节圆直径1.2m，采用6个爆炸螺栓连接；又如大型运载火箭长征五号（CZ－5）星箭连接节圆直径3m，采用12个螺栓连接。由于连接结构一般具有应力集中、边界非线性的问题，还可能伴随材料非线性、几何非线性的情况，并与预紧力、摩擦力等因素密切耦合［2］，导致此类结构的连接刚度下降，动力学特性分析较为困难，成为长期关注的研究热点。特别是，连接刚度变化会直接影响航天器的模态特性［3－5］，比如文献［6］发现连接刚度的损失对系统的弯曲模态有严重的影响。而航天器的基频及其对应模态是航天器结构设计的重要特性。因此，准确描述包含点式连接结构的动力学行为是一个极具应用价值，同时也亟待解决的问题。

目前，由于有限元软件不具备直接计算非线性连接结构模态的能力，传统的方法重点关注连接部位的简化建模方式，将非线性连接结构转化为线性结构，主要有三种方式：第一种是全固连建模方法，忽略连接的存在，将模型建立成不考虑螺栓连接和接触界面的全固连连续系统［6］，但是由于机械连接结构是不连续的，加之摩擦对接触界面的影响，使计算频率明显大于试验数据，给结构设计带来风险；第二种是节点约束方法，仅约束螺栓孔附近的区域［7］，此方法确实有效降低了固有频率，但由于结构的接触面积随载荷变化，其忽略了结构压缩状态和弯曲状态接触面积的变化情况，使点式连接结构计算频率偏低，增加了不必要的设计成本；第三种方法用杆单元、弹簧单元等模拟螺栓结构［8］，这种方法同样没有考虑接触面积随载荷的变化情况；所以这三种简化建模方法均不能真实反映连接特性。尤其针对点式连接结构，传统的计算结果往往与试验结果相去甚远，例如，当前国内在研的某大型卫星（上下串联的双星）的发射质量是3.9t，采用长征三号丙运载火箭（CZ－3C）发射，双星之间采用6个均布的分离螺母进行连接。运载火箭要求该卫星的横向一阶频率大于10Hz，基于传统的模态分析方法，建立两种线性模态分析模型：第一种仅将双星连接界面的6个连接点节点约束，计算频率为8Hz；第二种双星界面全部固连，计算频率为15Hz，两者差别高达87.5%，根本无法通过传统方法考量结构的真实模态。近十余年来，伴随着大规模工程结构仿真预测，发展起来一种描述接触界面间本构关系模型的方法，以模拟连接结构的动力学行为［9－10］，但是这些本构关系模型对参数有严格的要求，往往需要从大量的试验中获得，因而难以推广。

本文提出一种通过等效刚度计算航天器模态的方法。利用有限元模型［11－13］并结合非线性振动［14］和结构动力学［15］的原理计算点式连接的等效刚度。然后将等效刚度赋予点式连接航天器简化模型进行模态分析，与试验数据对比，验证了此方法的有效性。

2 点式连接航天器模态与等效刚度分析

2.1 模态分析

为了准确计算点式连接航天器的模态，本研究采用广义弹簧单元［16］，建立点式连接航天器有限元简化模型，通过给广义弹簧单元赋予连接刚度，可以准确计算点式连接航天器的模态。具体步骤为：

（1）静刚度计算：根据航天器结构，采用有限元分析软件进行接触分析，选择点式连接局部部位建立有限元接触分析模型，计算其3个方向的力－位移曲线和力矩－转角曲线，进一步计算拉压、弯曲和扭转静刚度曲线。

（2）等效刚度计算：根据本文2.2节所述的等效刚度计算方法，处理步骤1获得的静刚度曲线，分别计算轴向拉压等效刚度和弯曲等效刚度。

（3）航天器模态计算：建立航天器有限元模态分析模型，将点式连接部位用广义弹簧单元代替，将步骤2所得的等效刚度结果赋予广义弹簧单元，计算航天器的模态。

但是连接刚度随外激励的变化具有非线性特性，通过商用有限元软件对点式连接部位建立精细化有限元模型，能够获得点式连接的3条平动刚度曲线和3条转动刚度曲线，大量研究表明，除了扭转刚度曲线基本是线性的，其他连接刚度曲线都具有明显的非线性特性。但广义弹簧单元需要被赋予准确的刚度值才能计算点式连接的模态，如何通过非线性刚度曲线计算广义弹簧单元的刚度值（本文称为等效刚度），成为点式连接航天器模态分析的关键。因此，下文将围绕等效刚度计算进行深入探讨。

2.2 等效刚度分析

为了获得等效刚度，这里采用非线性振动［14］和结构动力学［15］的原理，计算非线性连接刚度曲线的等效刚度。图1是某航天器的器箭舱段连接结构示意图，它采用螺栓－法兰点式连接结构。为了便于理解，以图1坐标系为例介绍连接等效刚度的计算方法。因为航天器一般具有对称性，剪切刚度Ky＝Kz（Ky是y方向的剪切刚度，Kz是z方向的剪切刚度），弯曲刚度Kθy＝Kθz（Kθy是y方向的弯曲刚度，Kθz是z方向的弯曲刚度，θ为转角）。同时，点式连接航天器一般为长细结构，剪切刚度Ky（Kz）对结构模态的影响较小［17］，因此，本文将重点计算轴向拉压等效刚度Kx、弯曲等效刚度Kθy（Kθz）和扭转等效刚度Kθx，并假设剪切刚度为轴向拉压刚度的10倍，即Ky（Kz）＝10 Kx。

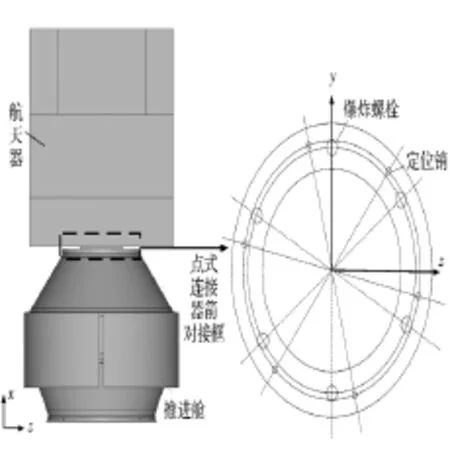
图1 点式器箭舱段连接结构示意图Fig.1 Separation nuts and joined parts

由于扭转刚度曲线是线性的，可以直接读取刚度值，而拉压刚度曲线和弯曲刚度曲线具有明显的非线性特性，须要计算等效刚度。

令K为点式连接非线性系统（轴向拉压或弯曲）的等效刚度，由结构动力学［15］可知

式中：T是非线性系统（轴向拉压或弯曲）自由振荡的运动周期，m是外力作用点处的集中质量。假设连接结构为保守系统，采用非线性振动［14］中计算分段线性保守系统的方法计算等效刚度。

2.2.1 轴向拉压等效刚度

大量研究表明，点式连接的拉伸和压缩刚度通常存在较大差异，因此整体显示出非线性特性［3］（参见3.1节）。忽略零点过渡段，点式连接在仅受拉或者受压时均可简化为独立的线性保守系统。保守系统的动力学方程一般形式为

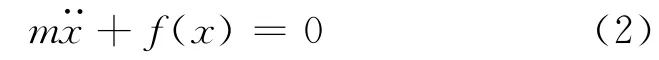
舱段连接系统的拉压恢复力f（x）是位移x的分段函数，

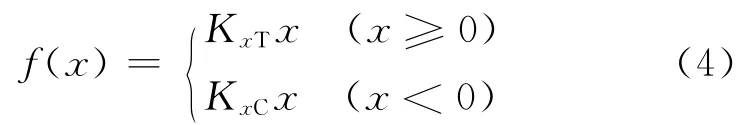
式中：KxT和KxC分别是拉伸段和压缩段的刚度，对应的势能和相轨迹方程分别为

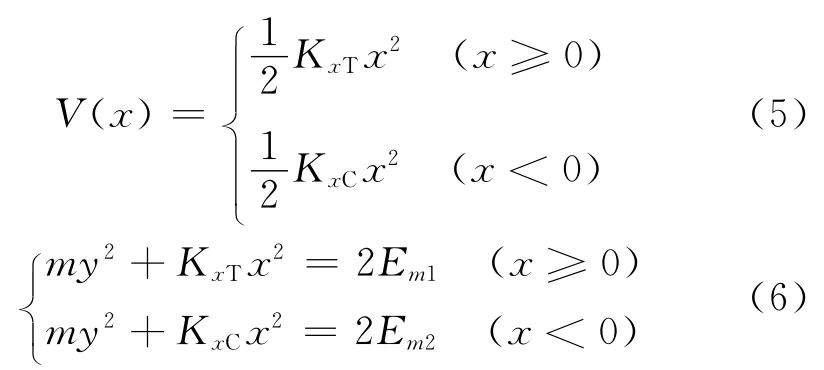
式中：V（x）是保守系统的势能，Em1和Em2分别是系统的拉伸段和压缩段的机械能。由相轨迹方程（6）可知，当速度y＝0时，得拉伸段和压缩段的幅值分别为

2.2.2 弯曲等效刚度

前期试验显示，点式连接的弯曲刚度具有分段线性特征（参见3.1节）。当外载荷较小时，弯曲刚度较小；随着载荷的增加，弯曲刚度增大。忽略过渡段，将弯矩作用下的点式连接简化为分段线性系统，则对应的弯曲恢复力f（θ）是转角θ的分段线性函数：

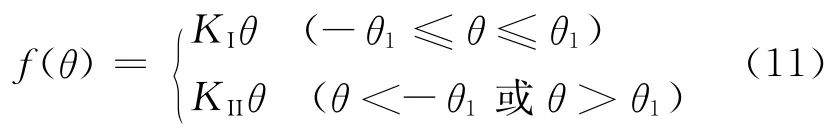
式中：KI和KII分别是小刚度段和大刚度段线性系统的刚度，θ1是弯曲刚度改变时对应的角度值。

一般地，在力学模态试验中，小刚度段范围较窄，弯曲刚度很快从小刚度段过渡到大刚度段，所以弯曲等效刚度包括小刚度KI和大刚度KII两部分，推导过程参考轴向拉压等效周期的计算方法，弯曲方向运动的周期为

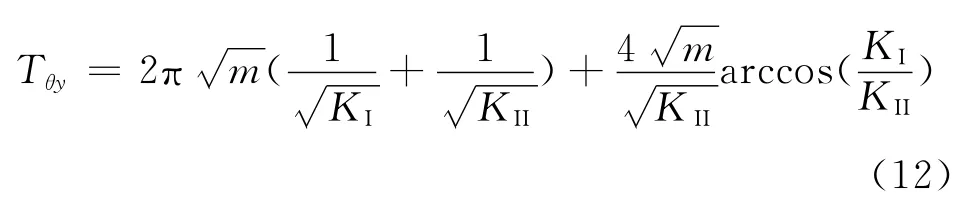
将式（12）代入式（1）获得弯曲等效刚度为

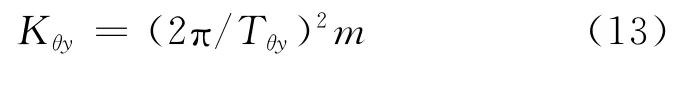
3 典型卫星承力筒结构模态分析算例

考虑到承力筒是国内外航天器极为常见的主承载结构，如DFH－3、DFH－4、SAST3000、SAST5000、EuroStar3000、AlphaBus等卫星平台。因此参照航天器的典型舱段连接结构，设计了一个卫星承力筒模型（见图2），由上承力筒1、下承力筒2和正方形配重块组成，通过若干个M6的螺栓将两筒连为一体（螺栓数目分别取4，8，16，24，32，48个），螺栓数目的递增代表了从点式连接过渡到普通舱段连接。模型尺寸如图2所示，材料参数见表1。

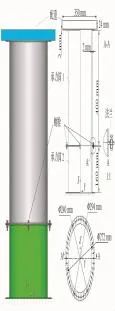
图2 卫星承力筒几何模型Fig.2 Assembled structure with bolted joints

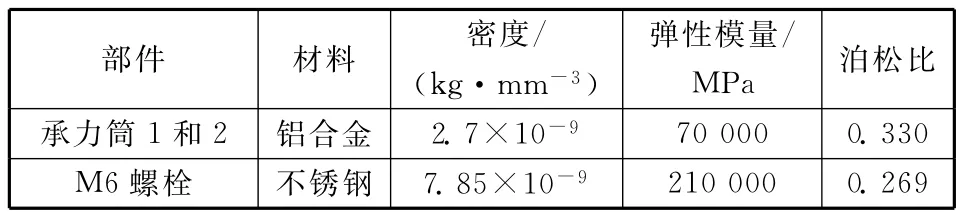
表1 卫星承力筒模型材料特性Table 1 Material properties of bolted joints

为了计算连接部位的等效刚度，取螺栓法兰区域建立三维有限元分析模型，尺寸如图3所示。外力作用点位于承力筒1上表面中点，与承力筒1上表面耦合约束，承力筒2的下表面固支约束。采用ABAQUS有限元软件对模型进行分析。有限元模型中，上下承力筒、法兰和螺栓均采用8节点实体单元。螺栓与法兰界面、上下法兰界面之间建立接触（如图3的粗实线所示），接触特性为法向硬接触、切向库伦摩擦（摩擦因数根据机械设计手册取0.05）。在每组工况下，参考紧固件拧紧力矩标准，螺栓的预紧力取4000N。模型约有293 472个单元和364 928个节点，可以满足计算收敛性的需求。

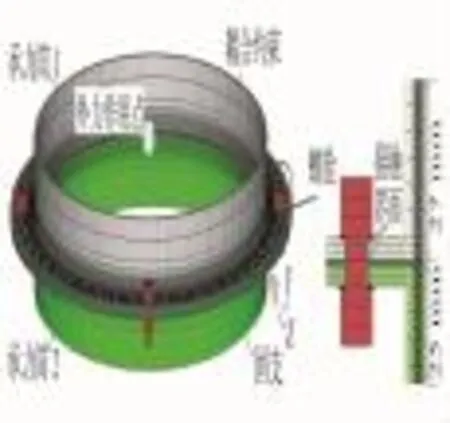
图3 螺栓法兰连接结构有限元模型Fig.3 FEM bolted flange joints

3.1 卫星承力筒连接刚度曲线

如图4所示，拉力FxT施加在外力作用点处，通过ABAQUS软件计算得到作用点的拉伸位移uxT，拉伸刚度KxT是拉力－拉伸位移曲线（图4（a）虚线右侧拉伸段）的斜率，即

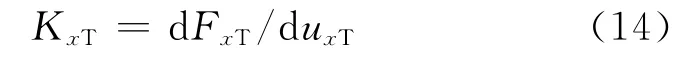
同理，压缩刚度KxC是压力FxC和压缩位移uxC曲线（图4（a）虚线左侧压缩段）的斜率，即

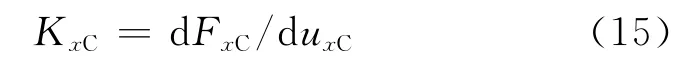
图4（b）是拉压刚度曲线，虚线右端是拉伸刚度，虚线左端是压缩刚度。可以看出，拉压刚度具有明显的非线性特性，即拉伸刚度远小于压缩刚度［3］。同时，压缩刚度与螺栓的数目基本无关，而拉伸刚度随螺栓数目的增加而增加。

在外力作用点施加±y（±z）方向的弯矩和±x方向的扭矩，获得相应的转角，参考式（14）或式（15）计算弯曲刚度Kθy（Kθz）和扭转刚度Kθx，计算结果见图5和图6所示。图5（a）是弯矩My和转角θy的曲线，图5（b）是弯曲刚度Kθy曲线，虚线左右分别是－θy转角和＋θy转角，弯曲刚度具有非线性特性。图6（a）是扭矩Mx和转角θx的曲线，图6（b）是扭转刚度Kθx曲线，虚线左右分别是－θx转角和＋θx转角，扭转刚度是线性的。与拉伸刚度类似，弯曲和扭转刚度随螺栓数目的增加而增加。

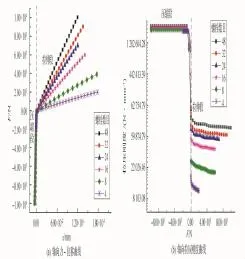
图4 轴向拉压静刚度曲线Fig.4 Tension and compression stiffness curves

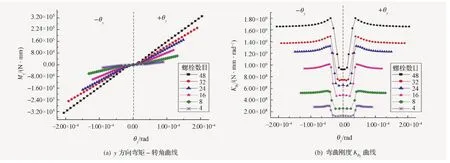
图5 弯曲静刚度曲线Fig.5 Bending stiffness curves

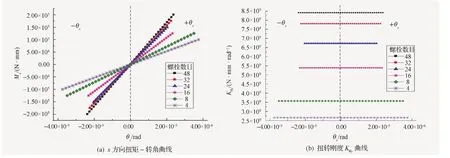
图6 扭转静刚度曲线Fig.6 Torsional stiffness curves

3.2 卫星承力筒等效刚度计算

图4是拉压刚度曲线，忽略零点的过渡区域，拉伸刚度和压缩刚度近似看作恒定的，可采用式（10）计算轴向等效刚度。图5中弯曲刚度曲线具有两条线性段，当外载荷较小时，弯曲刚度幅值较小且近似看作恒定的；随着载荷增加，弯曲刚度幅值成阶梯状增加，稳定后的结果也近似看作线性的；忽略过渡区域，将弯矩作用下的点式连接简化为分段线性系统，采用式（13）计算弯曲等效刚度。切向等效刚度取轴向等效刚度的10倍，扭转刚度直接从图6所示扭转刚度曲线读取，等效刚度具体数值见表2。

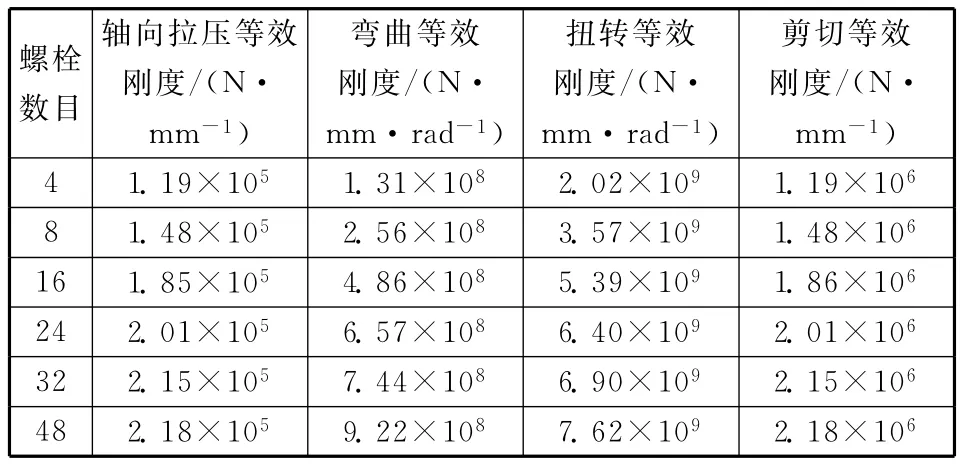
表2 等效刚度Table 2 Equivalent joint stiffness

从图4、图5和图6可以看出，连接结构的连接刚度随螺栓数目的增加而增加，表2也列出不同螺栓数目的等效刚度取值，为了进一步分析螺栓数目对连接刚度的影响，对等效刚度的取值归一化得

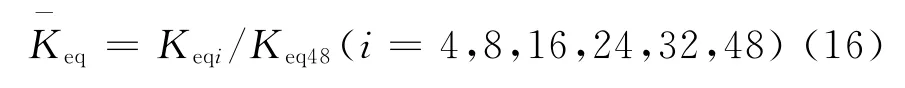
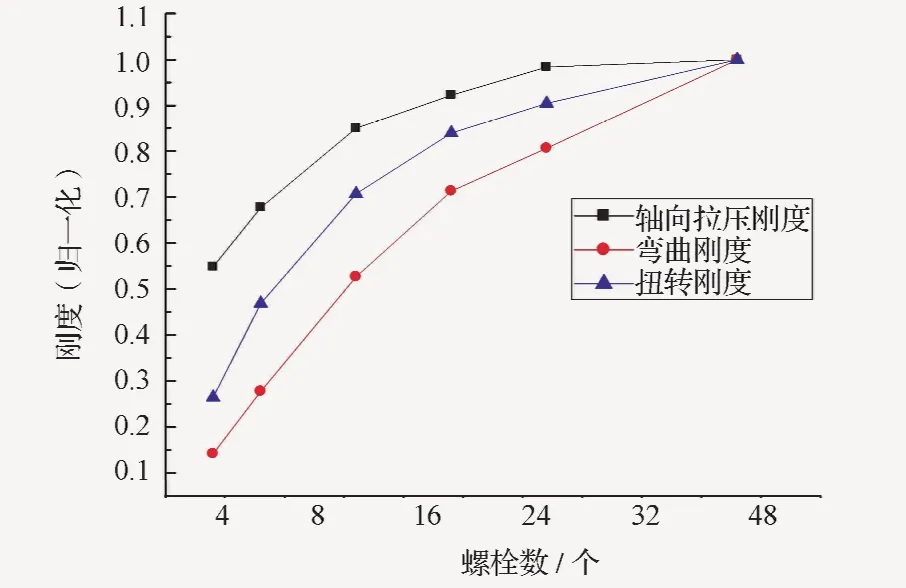
图7 刚度变化趋势曲线Fig.7 Stiffness trend curves

特别是，点式连接呈现明显的刚度衰减现象，相比于48个螺栓的等效刚度，4个螺栓的衰减幅值高达85%。显然，若不在建模过程中加以考虑点式连接的刚度衰减现象，将直接影响动力学分析结果的正确性。

3.3 卫星承力筒模态分析与试验验证

图8是卫星承力筒的有限元简化模型，采用MSC／Nastran有限元软件建模并分析模态。与图2中几何模型相同，结构由承力筒1、承力筒2和质量为22.92kg的配重组成。其中螺栓法兰连接结构（见图3）由广义弹簧单元（Nastran中即为Bush单元，其刚度矩阵是由6个自由度的对角阵组成［16］）代替。Bush单元的两端与承力筒1和2通过Mpc约束连接，Bush单元的刚度取表2中的等效刚度（根据螺栓数目的不同计算6组工况）。承力筒采用4节点壳单元，配重采用8节点实体单元，壳单元与实体单元通过Mpc约束连接［18］。承力筒2下表面48个螺栓孔附近的区域固支约束，材料参数与表1相同。

图9是螺栓法兰连接结构的模态试验示意图，试验系统包含试验件、加速度传感器（灵敏度是40mV／g）、力锤、LMS公司数据采集设备、LMS公司软件分析系统等。承力筒与配重的安装方式与图2相同。增加加速度传感器数量可以提高测试精度，但由于传感器质量增加对模态有影响，这里采用13个传感器，1个布置在配重顶部中心位置，另12个布置在承力筒1的上法兰根部、腹部和下法兰根部，均沿周向呈90°分布。力锤的锤击点分为A、B两处，点A在配重上表面中点，点B在配重侧面中点，每个测点用力锤敲击5次取样，通过LMS软件求均值，根据螺栓数目的不同测试6组工况。

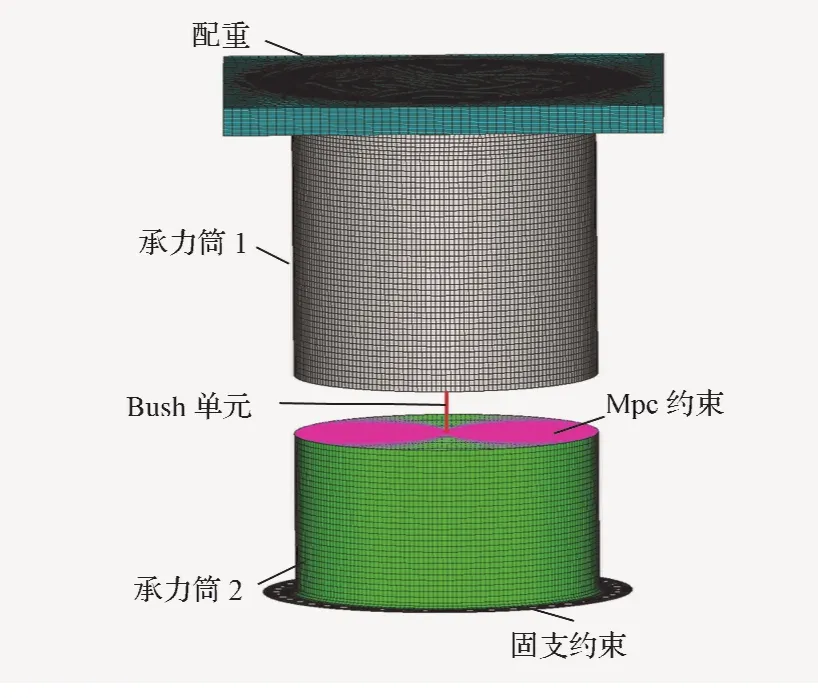
图8 有限元模型示意图Fig.8 FEM mode analytical specimen

图9 模态试验示意图Fig.9 Modal test specimen

表3列出了6组工况下试验和仿真的模态频率对比结果，航天器模态分析重点关注横向一阶弯曲模态、纵向一阶模态、横向二阶弯曲模态和扭转一阶模态，试验和仿真结果显示，频率误差基本在15%以内，仿真结果与试验数据吻合很好，等效刚度法适用于舱段连接结构的模态分析。尤其对于点式连接航天器，因为采用传统建模方法无法获得精确的模态，而等效刚度模态分析方法解决了连接刚度非线性对模态分析精度的影响。

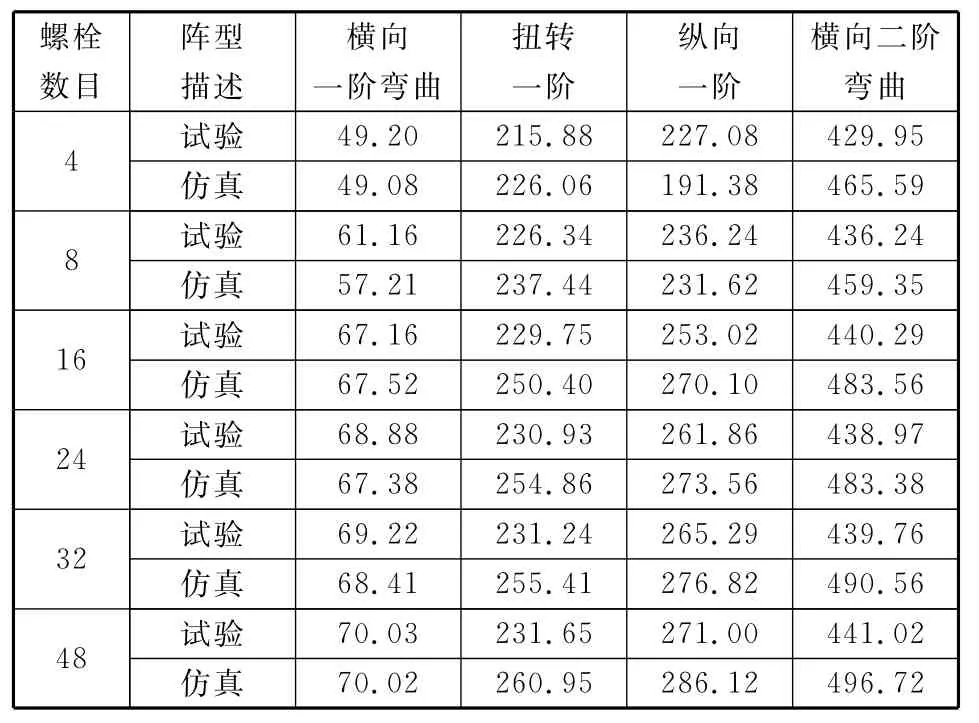
表3 仿真与试验模态频率对比Table 3 Frequency obtained from simulation and test Hz

从表3可以看出模态频率随螺栓数目的增加而增加，但增加的幅度随螺栓数目的增加而减小。对比点式连接（4个螺栓）和普通舱段连接（48个螺栓），频率下降高达30%，说明点式连接的螺栓数量对结构模态的影响很大，考虑螺栓数目变化引起连接刚度的变化，准确分析点式连接航天器的模态是很有必要的。

虽然螺栓数目有所不同，但不同工况下的振型基本相同，图10列出了8个螺栓仿真和试验振型的对比，证明仿真结果的正确性。

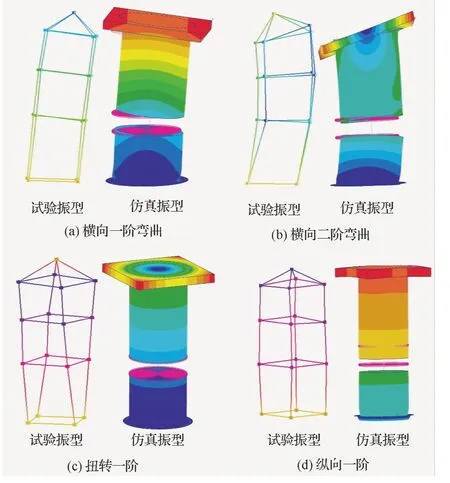
图10 仿真与试验振型对比Fig.10 Mode of vibration obtained from simulation and test

3.4 等效刚度模态法与传统分析方法对比

以4个螺栓的卫星承力筒点式连接计算模型为例，分别采用全固连建模方法和连接节点约束方法计算点式连接模型的模态，并与等效刚度模态分析方法和模态试验结果比较。全固连方法将上下承力筒连接部分节点融合，使其成为一个线性结构；连接节点约束方法仅将上下承力筒对应节点通过MPC约束，这里仅建立4个约束（见表4）。

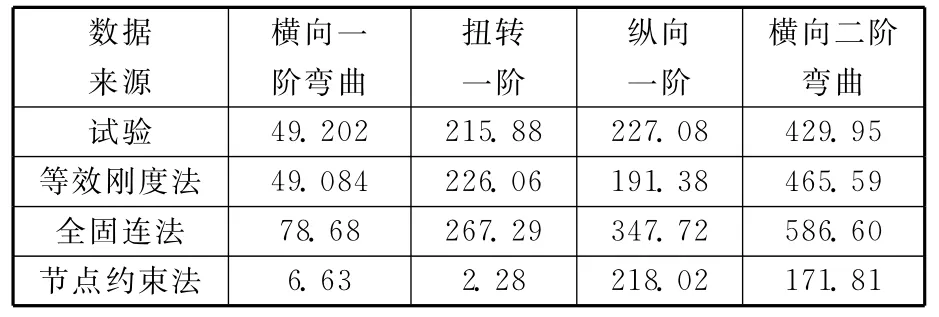
表4 模态分析结果Table 4 Results of modal analyses Hz

从表4模态分析结果的比较来看，全固连的模态计算结果与试验结果误差高达64%，连接节点约束方法无法计算出真实的模态频率，误差高达99%。因此，等效刚度模态分析方法对于连接结构的计算精度与其他方法的相比具有显著的优势，同时也说明传统的分析方法过于粗放和保守，不能满足现代航天器精细化设计计算的需求。

4 结论

点式连接已广泛应用于大型航天器舱段及部件级结构，本文针对模态分析中存在的技术难题，提出了一种采用等效刚度计算点式连接航天器模态的方法。运用非线性振动和结构动力学相关理论，计算出非线性连接结构的等效刚度，结合广义弹簧单元计算点式连接航天器的模态。主要结论有：

（1）采用广义弹簧单元计算的模态结果与模态试验数据对比，航天器的横向一阶、二阶弯曲，纵向一阶，一阶扭转模态误差小于15%，基本上在10%左右，证明了该方法计算点式连接航天器的有效性。

（2）本文定量地证明了点式连接的连接刚度随着螺栓数量的减少将呈现明显衰减，衰减幅度高达85%。

（3）仿真与试验结果均显示，点式连接与普通舱段连接相比，航天器整体的固有频率下降幅度高达30%，说明航天器设计中点式连接的静／动力学分析应予以高度重视。

（4）等效刚度模态分析方法可以准确分析航天器的模态，尤其针对连接点数目较少的点式连接航天器，解决了传统的全固连建模方法或连接节点约束方法计算不准确的问题。

本文所提出的等效刚度方法对于提高点式连接的航天器模态计算精度具有参考意义。

（References）

［1］赵超，周军，周凤岐.大型复合航天器的建模与分散控制技术［J］.飞行力学1998，16（3）：22－27 Zhao Chao，Zhou Jun，Zhou Fengqi.Modeling and decentralized control techniques for large compound spacecraft［J］.Flight Dynamics，1998，16（3）：22－27（in Chinese）

［2］郑晓亚，徐超，王焘，等.螺栓－法兰连接结构非线性优化设计方法研究综述［J］.强度与环境，2008，35（3）：7－13 Zheng Xiaoya，Xu Chao，Wang Tao，et al.Study on nonlinear optimization design for bolted flanged connection［J］.Structure ＆Environment Engineering，2008，35（3）：7－13（in Chinese）

［3］栾宇，刘松，关振群，等.小变形下螺栓法兰连接结构的静刚度［J］.强度与环境，2011，38（3）：29－35 Luan Yu，Liu Song，Guan Zhenqun，et al.The nonlinear character of static stiffness in the structure with bolted flanged connection under small deformation［J］.Structure ＆Environment Engineering，2011，38（3）：29－35（in Chinese）

［4］郑晓亚，张铎，姜晋庆.连接刚度对导弹固有特性的影响［J］.弹箭与制导学报，2005，25（4）：667－669 Zheng Xiaoya，Zhang Duo，Jiang Jinqing.The joint stiffness effect upon missile’s normal modes［J］.Journal of Projectiles，Rockets，Missiles and Guidance，2005，25（4）：667－669（in Chinese）

［5］Zhang O，Poirier J A.New analytical model of bolted joints［J］.Journal of Mechanical Design，2004，126（4）：721－728

［6］Wang C，Zhang D Y，Zhu X B，et al.Study on the stiffness loss and the dynamic influence on rotor system of the bolted flange joint［C］／／ASME Turbo Expo 2014：Turbine Technical Conference and Exposition.New York：ASME，2014

［7］程来，宋言明，李贺，等.基于等效接触区域的螺栓连接结构模态分析［J］.机械设计与研究，2012，28（2）：44－47 Cheng Lai，Song Yanming，Li He，et al.Modal analysis based on the equivalent contact area of the structure with bolt connections［J］.Machine Design ＆Research，2012，28（2）：44－47（in Chinese）

［8］薛闯，贾建军，舒嵘，等.装配体结构有限元分析中的螺钉连接模型［J］.科学技术与工程，2006，6（7）：825－828 Xue Chuang，Jia Jianjun，Shu Rong，et al.Bolted joint models of finite element assemblies［J］.Science Technology and Engineering，2006，6（7）：825－828（in Chinese）

［9］Segalman D J.A four－parameter Iwan model for laptype joints［J］.Journal of Applied Mechanics，2005，72（5）：752－760

［10］Mayer M H，Gaul L.Segment－to－segment contact elements for modelling joint interfaces in finite element analysis［J］，Mechanical System Signal Processing，2007，21（2）：724－774

［11］石亦平，周玉蓉.ABAQUS有限元分析实例详解［M］.北京：机械工业出版社，2006 Shi Yiping，Zhou Yurong.Detailed examples of ABAQUS finite element analysis［M］.Beijing：China Machine Press，2006（in Chinese）

［12］Kim J，Yoon J C，Kang B S.Finite element analysis and modeling of structure with bolted joints［J］.Applied Mathematical Modelling，2007，31（5）：895－911

［13］Yorgun C，Dalcl S，Altay G A.Finite element modeling of bolted steel connections designed by double channel［J］.Computers ＆Structures，2004，82（29）：2563－2571

［14］刘延柱，陈立群.非线性振动［M］.北京：高等教育出版社，2001：19－27 Liu Yanzhu，Chen Liqun.Nonlinear vibrations［M］.Beijing：Higher Education Press，2001：19－27

［15］余旭东.飞行器结构动力学［M］.西安：西北工业大学出版社，2012 Yu Xudong.Aircraft structure dynamics［M］.Xi’an：Northwestern Polytechnical University Press，2012（in Chinese）

［16］邹元杰.Bush有限单元原理及其在航天器结构建模中的应用［J］.航天器工程，2010，19（1）：99－105 Zou Yuanjie.Bush finite element principle and its application in building structural models for spacecraft［J］.Spacecraft Engineering，2010，19（1）：99－105（in Chinese）

［17］苟文选.材料力学［M］.西安：西北工业大学出版社，2000：183－185 Gou Wenxuan.Mechanics of materials［M］.Xi’an：Northwestern Polytechnical University Press，2012（in Chinese）

［18］龙凯.Patran2010与Nastran2010有限元分析从入门到精通［M］.北京：机械工业出版社，2010 Long Kai.Rudiments and mastery of Patran2010and Nastran2010FEA［M］.Beijing：China Machine Press，2010（in Chinese）

（编辑：张小琳）

Modal Analysis of Spacecraft with Dotted Joints Based on Equivalent Stiffness

SHI Chuanqian1ZHOU Xubin1ZHANG Yongtao1，2DU Dong1LI Hao1
（1Shanghai Institute of Satellite and Engineering，Shanghai 200240，China）（2Shanghai Lizheng Satellite Application Technology Co.，Ltd.，Shanghai 200240，China）

To include the interaction effect in modal analysis，a novel model analysis method employing the equivalent stiffness of dotted joints is proposed in this paper.Firstly，a full－size finite element model of a dotted joint for a spacecraft structure is established.The nonlinear connection stiffness of dotted joint corresponding to different bolt quantities and loads are predicted.A novel method based on nonlinear dynamic theory is proposed to calculate the equivalent stiffness of dotted joints.Then，a simplified FE model of the spacecraft structure is established by employing the generalized spring element and the calculated equivalent stiffness.The modes of the spacecraft structure are predicted by the simplified FE model and are also measured in experiments.The predicted modes coincide quite well with the experimental results.The proposed modal analysis method is proven to be accurate and will facilitate the dynamic analysis of spacecraft structure with dotted joints.

spacecraft；dotted joints；mode；equivalent stiffness；nonlinearity

V414.1

：ADOI：10.3969／j.issn.1673－8748.2016.01.005

2015－10－30；

：2015－12－28

国家重大航天工程

石川千，女，硕士研究生，从事卫星结构设计和结构非线性动力学研究工作。Email：shichuanqian＠163.com。