国产光学卫星影像几何精度研究

李德仁张过蒋永华沈欣，4

国产光学卫星影像几何精度研究

李德仁1，2张过1，2蒋永华2，3沈欣1，2，4

（1武汉大学测绘遥感信息工程国家重点实验室，武汉 430079）（2地球空间信息技术协同创新中心，武汉 430079）（3武汉大学遥感信息工程学院，武汉 430079）（4武汉大学资源与环境科学学院，武汉 430079）

受卫星设计和关键硬件制造水平的限制，我国高分辨率光学卫星影像的自主几何定位精度与国际先进水平仍有一定差距。针对在轨的国产光学卫星的影像几何精度问题，文章从误差源分析入手，提出了国产光学卫星影像几何精度提升理论和方法，通过在卫星数据处理过程中自动检测、消除包括设备安装，姿态、轨道测量，相机畸变，时间同步等多种误差，提高了卫星影像的几何精度；并对高分辨率卫星数据的几何精度提升状况进行了验证。结果表明：经过所提出的几何精度提升方法处理后，国产卫星的带控制点影像几何定位精度均可达到1.5像素，显著优于原设计指标。

遥感；光学卫星；几何精度；精度提升；平行观测

1 引言

高分辨率卫星遥感影像是国土资源普查、地形测绘、灾害应急、国防建设等国家重大任务的重要信息支撑，长期以来，我国一直对高分辨率光学遥感卫星影像数据保持着旺盛需求。自2007年9月成功发射资源一号02B卫星（全色分辨率2.36m）后，我国陆续发射了多颗高分辨率光学卫星，影像分辨率从米级逐步提升至亚米级，使我国自主获取全球高精度地理信息能力得到大幅提高。

但是，我们也清醒地意识到与国外先进国家相比，国产高分辨率卫星存在着影像几何精度不足的问题。针对该问题，长期以来有众多的研究人员对我国高分卫星影像几何精度提升做了相关研究并取得了一定成果，但鲜有文献较为系统地研究我国高分卫星影像几何精度提升方法及几何精度的验证。

本文从误差源分析出发，提出了系统、完善的影像几何精度提升方法，开展了我国现役在轨主要高分辨率光学卫星影像几何精度提升试验，并利用多区域收集的高精度控制点验证了卫星影像的几何精度。试验表明：采用本文提出的“以软补硬”的数据处理方法处理后，国产卫星的影像几何精度可得到有效提升。

2 国产高分光学卫星影像几何精度影响因素分析

作者团队通过参与多颗国产高分遥感卫星影像几何处理系统研制，以及深入分析卫星的自身特点，总结了影响高分光学影像几何精度的主要因素，其主要包括：

（1）国产高分辨率卫星下传姿态频率普遍较低（0.25～4Hz），卫星平台的稳定度多数仅能控制在0.001（°）／s以内，造成了“高频姿态误差”。另一方面，由于受星上姿态数值基本计量单位限制（资源1号02C、遥感4号、实践9号A的姿态数值均以0.005 5°为基本单位，快舟2号、吉林1号A星的姿态数值均以0.005 7°为基本单位），使得测量姿态无法被精确记录，也造成了“姿态误差”。

（2）国产早期在轨高分辨率卫星还未采用高精度授时系统，时间同步误差造成了几何畸变。

（3）除资源3号卫星外，其余高分辨率卫星均采用较大畸变光学系统，但在轨几何检校研究起步较晚，到目前为止固定可用的高精度在轨几何检校场数据很少，未经严格几何检校的高分辨率影像存在较大畸变。

3 国产高分光学卫星影像几何质量提升方法

3.1 严密几何成像模型

国产高分辨率光学卫星采用线阵推扫成像模式，依据三点共线原理可以构建统一形式的严密几何成像模型［1－3］如下：

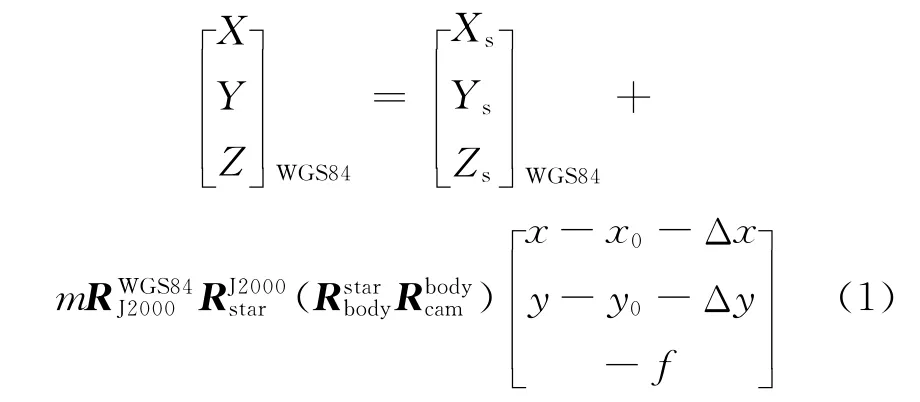
由式（1）可知，姿轨测量、设备安装差误等均会影响卫星影像几何精度。考虑到几何精度包括无控制定位精度提升和带控制定位精度提升，可将星上的众多误差作如下分类：

（1）影响无控制定位精度误差：包括设备安装误差（相机安装误差、测姿设备安装误差、测轨设备安装误差），姿态、轨道测量系统误差。这些误差可以通过地面控制点消除。

（2）影响带控制定位精度误差：包括相机畸变、高频姿态误差、时间同步误差。由于这些误差表现为高阶畸变或时变特征，通常难以利用地面控制点消除。

针对各类误差对影像几何定位精度的影响特性，构建误差补偿模型，提升无控制定位精度和带控制定位精度。

3.2 提升无控制定位精度

设备安装误差包括安装角误差及安装平移误差，考虑到设备安装角误差与姿态测量误差等效，而安装平移误差与轨道测量系统误差高度相关，可将影响无控制定位精度的误差统一为角度误差及平移误差。国产高分辨率光学卫星载荷普遍为小视场角；而在小视场角推扫成像条件下，线角元素存在较强相关性，同时解求两者容易引起解的不稳定。且在遥感卫星运行高度，线元素误差与角元素误差对几何定位精度的影响具有等效性，可将线元素误差等效成姿态角误差，从而采用偏置矩阵对影响无控制定位精度的众多误差进行统一补偿［4－6］。

3.3 提升带控制定位精度

3.3.1 内方位元素检校——消除相机畸变误差

国产高分辨率光学卫星均采用多片TDI CCD线阵拼接推扫成像，CCD线阵在焦面的摆放位置如图1所示；不同卫星重叠像素（Overlap）及沿轨错位均不同。

图1 CCD线阵摆放示意图Fig.1 CCD setting diagram

由于CCD线阵安置精度及相机畸变地面测量的精度有限，卫星在轨后不可避免的存在内方位元素误差。若针对各颗高分辨率卫星载荷CCD线阵特征对式（1）中的（Δx，Δy）建立不同的畸变模型，以完成在轨内方位元素检校，工作量非常大。为此，引入指向角模型［6－9］作为高分辨率光学卫星在轨内方位元素检校的统一模型。

3.3.2 消除高频姿态误差／时间同步误差

由式（1），时间同步误差可直观地理解为利用错误时刻的“轨道”、“姿态”数据处理当前扫描时刻的影像，实质上可看成时变的轨道误差、姿态误差，且变化速率与卫星当前的运行速度、姿态稳定度相关：如果卫星平稳运行，其表现为低频轨道和姿态误差；否则为高频轨道和姿态误差。由于国产高分辨率光学卫星的姿态稳定度限制，时间同步误差应等效为高频轨道和姿态误差。另外，根据3.2节，国产高分辨率卫星小视场推扫成像条件可以进一步将轨道误差等效为姿态误差，因此仅须要考虑消除高频姿态误差。

根据图1所示的CCD线阵布放情况，国产高分辨率光学卫星能够在非常短时间内在相邻CCD线阵重叠像素区域对同一地物点成像（图2）。

假定影像几何中不存在任何误差，则图2中同名像点p0、p1交会于地面同一点S，其中t0为S点第一次成像时刻，t1为S点的第二次成像时刻。内方位元素误差、高频姿态误差及高程误差均会带来p0、p1的交会误差。针对国产高分辨率光学卫星载荷，考虑到图1中θ1与θ0相差很小（一般不小于0.5°），当利用全球90m航天飞机地形测量任务（SRTM）数据辅助p0、p1交会时，高程误差对交会误差的影响可以忽略不计。因此，在完成高精度在轨内方位元素检校后，通过在相邻CCD影像重叠像素区域获取同名点，可以依据该原理探测并消除高频姿态误差［6］。

图2 平行观测Fig.2 Parallel observation

3.4 提升几何精度流程

综上所述，提升国产高分辨率光学卫星影像几何精度的流程如下：

（1）收集高精度几何检校场区域的所有卫星影像；

（2）利用高精度几何检校场控制数据，按上述3.2节方法解算偏置矩阵用以提升无控制定位精度；

（3）利用（2）中解算的偏置矩阵，按照3.3.1节方法进行内方位元素检校；

（4）完成（2）、（3）步骤后，统计各景影像的定位残差；如果定位残差普遍存在类高频的时变特性，则按3.3.2节方法利用平行观测进行高频姿态误差检测、补偿处理。

4 结果与分析

4.1 验证数据及提升方法

本文利用覆盖检校场区域的各高分辨率光学卫星影像进行在轨检校获取外、内方位元素检校参数，用以提升其余区域的无控制、带控制定位精度，针对存在高频姿态误差或时间同步误差的国产高分卫星，采用高精度配准算法，在相邻CCD上获取同名像点用以消除误差，不需要额外的控制数据。主要控制数据是，登封检校场和天津检校场的1∶2000数字正射影像（DOM）和数字高程模型（DEM），其中，登封检校场数据采集于2010年，区域内基本是平原，在西南角存在高差600m的山地，覆盖范围为50km×50km；天津检校场数据采集于2008年，区域内均为平地，高差小于12m，具体数据见图3。

图3 用于几何质量提升的控制数据Fig.3 Control data used for geometric quality improvement

利用1∶2000河南、天津检校场控制数据对主要国产高分辨率光学卫星定位精度进行分析，最终确定具体提升方法如表1所示。

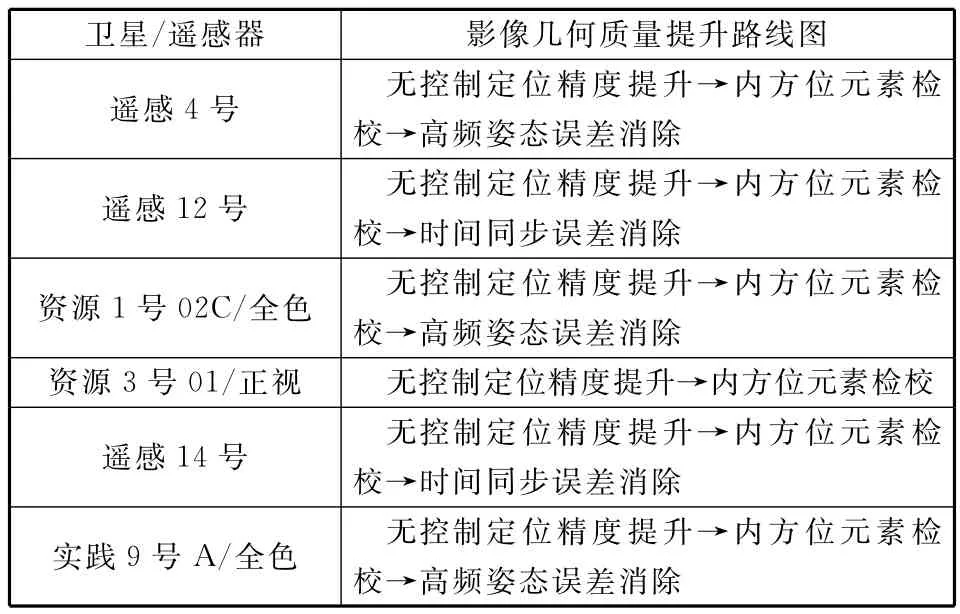
表1 国产高分辨率光学卫星影像几何质量提升路线图Table 1 Roadmap of image geometric qualityimprovement for domestic high resolution optical satellites

4.2 提升无控制定位精度验证

利用成像于2012－03－27的遥感12号卫星数据及登封检校场控制数据解求偏置矩阵，用该偏置矩阵补偿不同成像时间、不同区域的遥感12号卫星影像，利用高精度控制数据评价其几何定位精度如表2所示。

表2 提升遥感12号卫星无控制定位精度验证Table 2 Verification of positioning precision improvement of YG－12image without control points

由表2，利用2012－03－27获取的检校偏置矩阵，多数景无控制定位精度均优于50m，但2012－01－03和2012－10－18两景无控制定位精度较差。通过对试验影像遥测数据分析发现，除2012－01－03景、2012－10－18景影像星上定姿模式分别为3、4外，其余景星上定姿模式均为2；遥感12号卫星星上搭载有三个星敏感器（A、B、C），其成像通常采用侧摆模式，星上根据各星敏感器观测恒星情况选择其中两个星敏感器进行姿态确定，由于不同星敏感器组合对应的星敏感器安装误差不同，因此不同定姿模式下无法进行偏置矩阵补偿。

同样的，利用成像于2013－03－05的遥感14号卫星影像及登封检校场控制数据解求偏置矩阵，其对提升无控制定位精度验证见表3。

表3 提升遥感14号无控制定位精度的验证Table 3 Verification of positioning precision improvement of YG－14image without control points

由表3可见，仅仅采用2013－03－05景获取的偏置矩阵补偿，不同时间成像的四景影像无控制定位精度均优于100m；值得注意的是，除2012－10－27景外，其余景无控制定位精度均优于20m。考虑到遥感14号卫星在常态模式下采用侧摆成像，成像环境变化剧烈，载荷安装等系统性误差会因环境变化而变化，因此偏置矩阵具有一定时效性；由于2012－10－27景相隔2013－03－05景较远，星上系统误差可能发生改变，导致补偿后无控制定位精度并不很高；而其余三景与2013－03－05景时间间隔不超过半年，补偿后的无控制定位精度较高。因此，可以采用每隔较短时间（如半年）进行一次检校获取偏置矩阵，以保障无控制几何定位精度。

采用2012－02－03景资源3号01星正视影像解求偏置矩阵后，无控制定位精度优于20m，如表4所示。

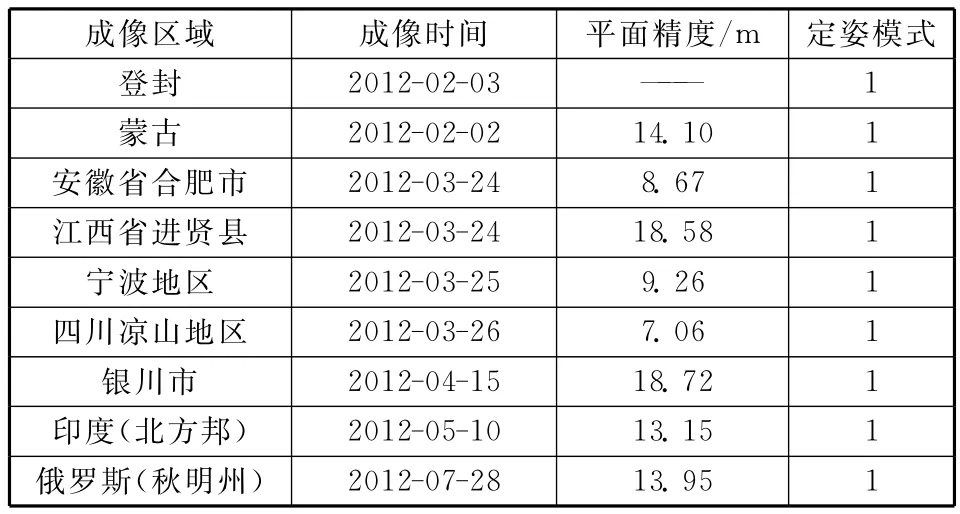
表4 提升资源3号01星正视无控制定位精度验证Table 4 Verification of positioning precision improvement of ZY3－01／NAD image without control points

但是，同样的无控制定位精度提升方法并没有在遥感4号、资源1号02C／全色、实践9号A／全色得到好的提升结果。表5中以资源1号02C／全色为例，可以看到无控制定位精度低，且很不稳定。事实上，遥感4号、资源1号02C、实践9号A三颗卫星星上均搭载有星敏感器，能以较高精度测量卫星在J2000坐标系下的姿态四元数；但卫星设计方为便于姿轨控制，在星上利用地面注入的预报轨道根数将姿态四元数转换成了轨道坐标下的欧拉角，并下传至地面用于后续几何处理；由于所采用的预报轨道根数精度有限，导致转换后的欧拉角精度低，使得这三颗卫星无控制定位精度很差。由于这三颗卫星均未下传原始测量的姿态四元数，采用同样的处理方法难以进一步提升、验证其无控制定位精度。目前主要采用收集的全球控制数据维持这三颗卫星的影像几何定位精度。

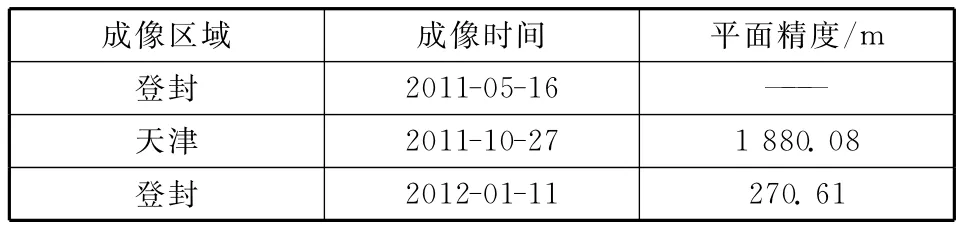
表5 提升资源1号02C／全色无控制定位精度验证Table 5 Verification of positioning precision improvement of ZY1－02Cpanchromatic image without control points

4.3 提升带控制定位精度验证

为验证带控制定位精度，同步收集了我国境内多个区域的控制数据及高分辨率光学卫星影像；验证试验涉及的控制区域如图4所示。

图4 带控制定位精度提升验证区域Fig.4 Improvement verification district with control points

4.3.1 消除相机畸变误差

主要国产高分辨率光学卫星中，除了资源3号01星各个载荷采用无畸变光学系统，内方位元素误差较小，其余各颗卫星均存在较大光学系统畸变，须要经过高精度在轨内方位元素检校，消除影像高阶畸变，提升带控制定位精度。

收集各颗高分辨率光学卫星覆盖登封、天津控制区域的影像，采用高精度配准算法在影像上获取大量均匀分布的高精度控制点，对各颗卫星载荷内方位元素进行检校，其检校精度评价如表6所示。

表6中，EO、IO分别表示未消除相机畸变和消除相机畸变后解算偏置矩阵的精度；其中，EO精度体现了相机畸变量级，而IO体现了在轨内方位元素检校精度。由于资源3号01星各个载荷采用无畸变光学系统，其NAD相机的实验室测量内方位元素精度优于0.3像素，经过在轨几何检校后精度提升至0.2像素；而其余各颗高分辨率光学卫星相机畸变较大（15～100像素），这主要是因为：①早期发射卫星在地面阶段并未对相机参数进行严格测量，因此初始内方位元素误差大；②早期发射卫星没有进行充分的温控设计，发射在轨后相机参数发生变化。同时可看到，采用高精度控制数据，各颗卫星在轨内方位元素检校精度均优于0.8像素，其精度主要受限于影像配准精度（依赖于检校影像的清晰程度、适合配准程度）。为突出相机畸变消除效果，图5以遥感4号卫星为例，对比了内方位元素检校前后的带控制定位精度。由图5（a）可看到，由于各片CCD独立安装于焦面不同位置，各片CCD畸变误差不同；通过内方位元素检校后，图5（b）已不再具备相机畸变特征。

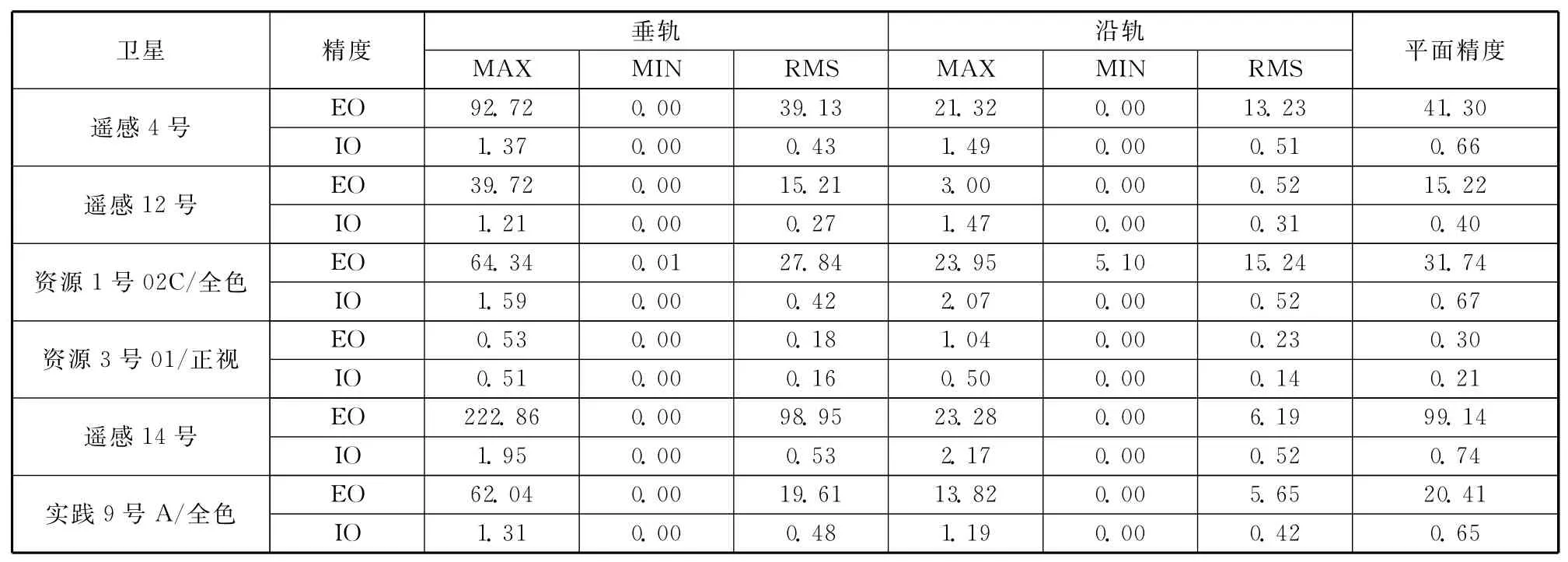
表6 国产高分辨率光学卫星内方位元素检校精度Table 6 Calibration result of inner orientation elements of domestic high resolution optical satellite像素

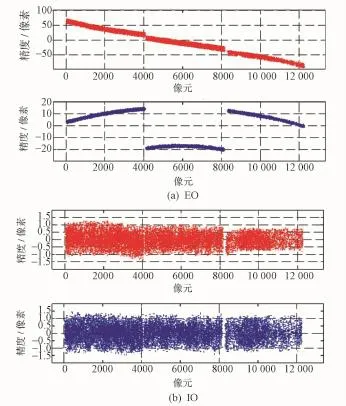
图5 遥感4号在轨内方位元素检校残差图Fig.5 Residual of onboard inner orientation elements calibration of YG－4

4.3.2 消除高频姿态误差／时间同步误差

如表1所示，高分辨率光学卫星须要进一步消除高频姿态误差或时间同步误差。下文以遥感12号卫星为例，给出消除其时间同步误差的结果。

由图2所知，若存在时间同步误差，相邻CCD同名点将无法交会于地面同一点；因此，可以通过比较消除时间同步误差前后相邻CCD交会精度来评价精度。表7中收集了天津、登封区域四景遥感12号影像，对比了消除时间同步误差前后的同名点交会精度。

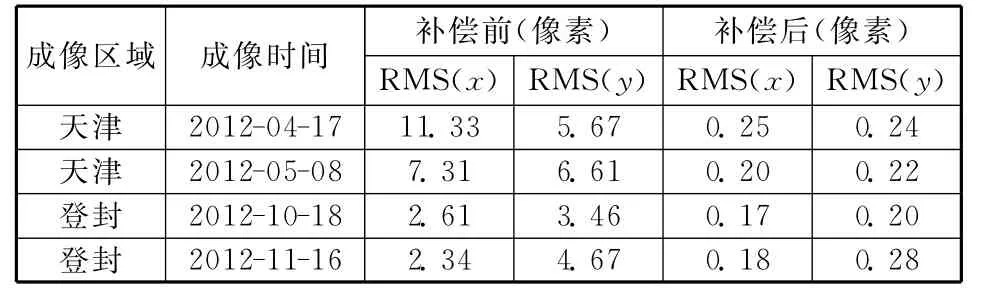
表7 同名点交会误差Table 7 Rendezvous error of homonymy points

由表7，消除时间同步误差后，同名点交会精度得到很大提升，垂轨、沿轨方向均优于0.3像素；图6以2012－04－17天津景给出了同名点交会残差对比图，可以明显看到时间同步误差引起的影像内部畸变非常复杂，即使有足够地面控制点也难以消除；而通过本文提升方法，在无须额外地面控制点的条件下消除了时间同步误差，提升了影像内部精度。

图6 2012－04－17天津景同名点交会误差Fig.6 Rendezvous error of homonymy points in 2012－04－17Tianjin image

4.3.3 拼接影像定向精度验证

由于国产高分辨率光学卫星载荷CCD线阵均按图1所示布放，须要对各颗高分光学卫星原始影像进行拼接后才能后续应用。按表1所示步骤消除各颗高分辨率光学卫星成像几何误差后，本文采用虚拟重成像技术［7－8］生成拼接影像及有理多项式系数（RPCs）：

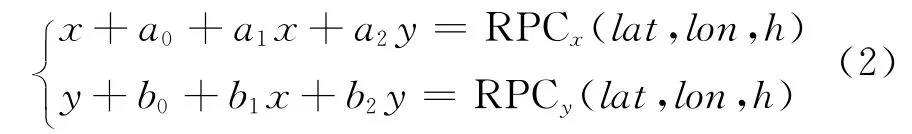
显然，拼接影像的拼接效果及RPCs定位精度完全依赖于严密几何成像模型的几何定位精度。可以直接评价RPCs带控制定位精度，以验证提升后的几何定位精度，如表8～表13所示。本文采用基于RPC的像面仿射模型［3，10－15］作为定向模型评价带控制几何定位精度。

其中，控制点数量超过100的均是采用高精度配准算法从DOM上配准获取。

由表8到表13可知，除遥感4号卫星外，其余各颗卫星四个控制点的定位精度均优于1.5像素，其中资源3号01星正视影像带控制定位精度最高，优于0.5像素，这一方面是因为资源3号01星成像时能很好地保持平稳运行，另一方面也是因为其采用的①、③类型控制点精度较高。而对遥感4号卫星，其天津景、登封景的稀少控制点定位精度均优于1像素，但其余区域稀少控制点定位精度在1.5～2像素，深入分析发现主要是受限于控制点像点坐标精度：由于遥感4号卫星影像成像模糊，辐射质量较低（如图7所示），加大了控制点选取难度，因此人工选取的控制点精度较低。

图7 遥感4号卫星影像局部示意图Fig.7 Local image of YG－4

表8 提升遥感4号带控制定位精度验证Table 8 Verification of positioning precision improvement of YG－4image with control points

表9 提升遥感12号带控制定位精度验证Table 9 Verification of positioning precision improvement of YG－12image with control points

表10 提升资源1号02C／全色带控制定位精度验证Table 10 Verification of positioning precision improvement of ZY1－02Cpanchromatic image with control points

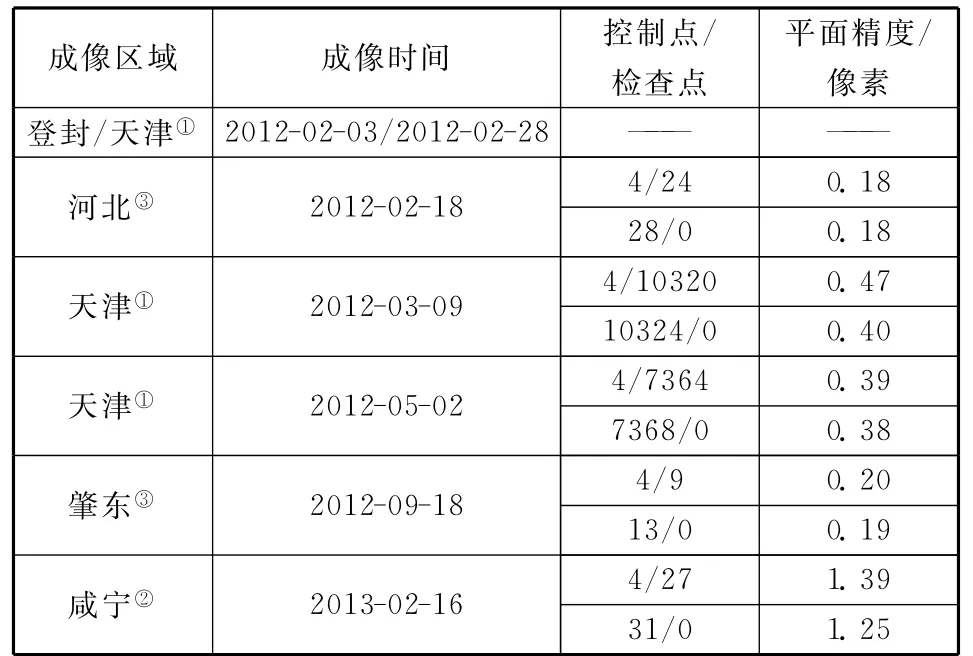
表11 提升资源3号01／正视带控制定位精度验证Table 11 Verification of positioning precision improvement of ZY3－01／NAD image with control points

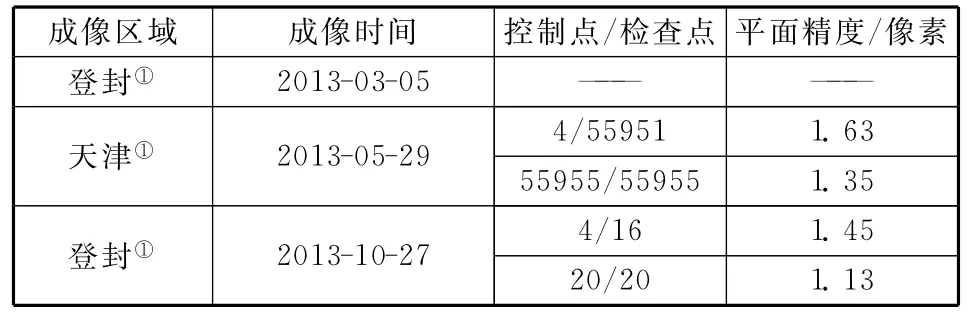
表12 提升遥感14号带控制定位精度验证Table 12 Verification of positioning precision improvement of YG－14image with control points

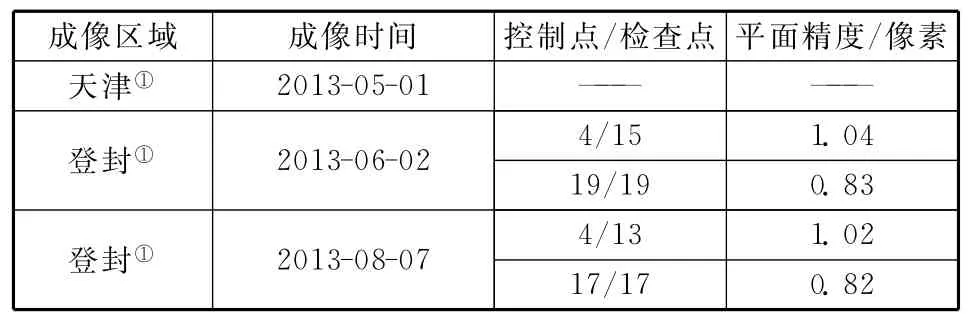
表13 提升实践9A带控制定位精度验证Table 13 Verification of positioning precision improvement of SJ－9Aimage with control points

总而言之，经过带控制定位精度提升方法处理后，我国各颗高分辨率光学卫星带控制几何定位精度基本优于1.5像素，与控制精度相当。说明本文方法针对我国高分辨率光学卫星缺陷能够较好地消除几何误差。

5 结论

本文识别出了当前我国主流高分辨率光学卫星影像存在的几何误差源，建立了我国高分辨率光学卫星的统一严密几何成像模型，针对星上稳定性系统误差及高频误差特征，系统地提出了我国高分辨率光学卫星无控制／带控制定位精度提升方法及流程。试验部分收集了多时段、多区域的各颗高分辨率光学卫星影像数据，试验结果表明：

（1）针对无控制定位精度提升，合理确定遥感12号、资源3号01星、遥感14号卫星求取偏置矩阵的周期，可以使三颗卫星保持较高精度的无控制定位精度；而对于遥感4号、资源1号02C、实践9号A三颗卫星，由于星上转换误差大，难以用偏置矩阵的方法提升无控制定位精度，当前仅能采用全球控制点库保障其无控制定位精度。

（2）而对于带控制定位精度，虽然我国高分辨率光学卫星有不同的设计指标要求，存在时间同步误差大、姿态遥测数据精度低等问题，但采用本文所提供的提升方法后，当前主流高分辨率光学卫星的带控制定位精度基本优于1.5像素，达到与控制精度相当的程度。

试验结果表明：在卫星设计和硬件水平受限条件下，通过“以软补硬”的误差处理方法，国产高分辨率光学卫星仍然可以达到较高的几何定位精度。随着我国航天技术的稳步提升和卫星检校场等基础设施的不断完善，相信在不久的将来，我国高分辨率光学卫星整体技术水平将有更大的提高。

（References）

［1］袁修孝，张过.缺少控制点的卫星遥感对地目标定位［J］.武汉大学学报（信息科学版）2003，28（5）：505－509 Yuan Xiuxiao，Zhang Guo.Object location of satellite imagery under lacking ground control points［J］.Geomatics and Information Science of Wuhan University，2003，28（5）：505－509（in Chinese）

［2］袁修孝，张过，吴春华.缺少控制点的卫星遥感影像外推定位［J］.武汉大学学报（信息科学版），2005，30（7）：575－579Yuan Xiuxiao，Zhang Guo，Wu Chunhua.Extrapolative location of high resolution remote sensing imageries［J］.Geomatics and Information Science of Wuhan University，2005，30（7）：575－579（in Chinese）

［3］张过.缺少控制点的高分辨率卫星遥感影像几何纠正［D］.武汉：武汉大学，2005 Zhang Guo.Rectification for high resolution remote sensing image under lack of ground control points［D］.Wuhan：Wuhan University，2005（in Chinese）

［4］祝小勇，张过，唐新明，等.资源一号02B卫星影像几何外检校研究及应用［J］.地理与地理信息科学，2009（3）：16－18，27 Zhu Xiaoyong，Zhang Guo，Tang Xinmin，et al.Research and application of CBRS02Bimage geometric exterior calibration［J］.Geography and Geo－Information Science，2009（3）：16－18，27（in Chinese）

［5］张过，袁修孝，李德仁.基于偏置矩阵的卫星遥感影像系统误差补偿［J］.辽宁工程技术大学学报，2007（4）：517－519 Zhang Guo，Yuan Xiuxiao，Li Deren.Redressing system error in satellite image based on bias matrix［J］.Journal of Liaoning Technical University，2007（04）：517－519（in Chinese）

［6］蒋永华，张过，唐新明，等.资源三号测绘卫星多光谱影像高精度谱段配准［J］.测绘学报，2013，42（6）：884－890，897 Jiang Yonghua，Zhang Guo，Tang Xinming，et al.Research on the high accuracy band－to－band registration method of ZY－3multispectral image［J］.Acta Geodatica et Cartographica Sinica，2013，42（6）：884－890，897（in Chinese）

［7］张过，刘斌，江万寿，等.推扫式光学卫星遥感影像产品三维几何模型研究及应用［J］.遥感信息，2011（2）：58－62 Zhang Guo，Liu Bin，Jiang Wanshou，et al.Study and application of three－dimension geometric model of products of push－broom optical satellite image［J］.Remote Sensing Information，2011（2）：58－62（in Chinese）

［8］潘红播，张过，唐新明，等.资源三号测绘卫星传感器校正产品几何模型［J］.测绘学报，2013，42（4）：516－522 Pan Hongbo，Zhang Guo，Tang Xinming，et al.The geometrical model of sensor corrected products for ZY－3 satellite［J］.Acta Geodatica et Cartographica Sinica，2013，42（4）：516－522（in Chinese）

［9］唐新明，张过，祝小勇，等.资源三号测绘卫星三线阵成像几何模型构建与精度初步验证［J］.测绘学报，2012，41（2）：191－198 Tang Xinming，Zhang Guo，Zhu Xiaoyong，et al.Triple linear－array imaging geometry model of Ziyuan－3sur－veying satellite and its validation［J］.Acta Geodatica et Cartographica Sinica，2012，41（2）：191－198（in Chinese）

［10］张过，厉芳婷，江万寿，等.推扫式光学卫星影像系统几何校正产品的3维几何模型及定向算法研究［J］.测绘学报，2010，39（1）：34－38 Zhang Guo，Li Fangting，Jiang Wanshou，et al.Study of three－dimensional geometric model and orientation algorithm for systemic geometric correction product of push－broom optical satellite image［J］.Acta Geodatica et Cartographica Sinica，2010，39（1）：34－38（in Chinese）

［11］张过，李德仁，袁修孝，等.卫星遥感影像的区域网平差成图精度［J］.测绘科学技术学报，2006，23（4）：239－241，245 Zhang Guo，Li Deren，Yuan Xiuxiao，et al.The mapping accuracy of satellite imagery block adjustment［J］.Journal of Geomatics Science and Technology，2006，23（4）：239－241，245（in Chinese）

［12］汪韬阳，张过，李德仁，等.资源三号测绘卫星影像平面和立体区域网平差比较［J］.测绘学报，2014，43（4）：389－395，403 Wang Taoyang，Zhang Guo，Li Deren，et al.Comparison between plane and stereo block adjustment for ZY－3satellite images［J］.Acta Geodatica et Cartographica Sinica，2014，43（4）：389－395，403（in Chinese）

［13］汪韬阳，张过，李德仁，等.卫星遥感影像的区域正射纠正［J］.武汉大学学报（信息科学版），2014，39（7）：838－842 Wang Taoyang，Zhang Guo，Li Deren，et al.block ortho－rectification for satellite images［J］，Geomatics and Information Science of Wuhan University，2014，39（7）：838－842（in Chinese）

［14］张过，潘红播，唐新明，等.资源三号测绘卫星长条带产品区域网平差［J］.武汉大学学报（信息科学版），2014，39（9）：1098－1102 Zhang Guo，Pan Hongbo，Tang Xinming，et al.Block adjustment of ZY－3long strip scenes［J］，Geomatics and Information Science of Wuhan University，2014，39（9）：1098－1102（in Chinese）

［15］张过，汪韬阳，李德仁，等.轨道约束的资源三号标准景影像区域网平差［J］.测绘学报，2014，43（11）：1158－1164 Zhang Guo，Wang Taoyang，Li Deren，et al.Block Adjustment for ZY－3satellite standard imagery based on strip constraint［J］.Acta Geodatica et Cartographica Sinica，2014，43（11）：1158－1164（in Chinese）

（编辑：张小琳）

Research on Image Geometric Precision of Domestic Optical Satellites

LI Deren1，2ZHANG Guo1，2JIANG Yonghua2，3SHEN Xin1，2，4
（1State Key Laboratory of Information Engineering in Surveying，Mapping and Remote Sensing，Wuhan University，Wuhan 430079，China）（2Collaborative Innovation Center of Geospatial Technology，Wuhan 430079，China）（3School of Remote Sensing and Information Engineering，Wuhan University，Wuhan 430079，China）（4School of Resource and Environmental Sciences，Wuhan University，Wuhan 430079，China）

Because of the defects in satellite design and key hardware manufacturing，there is still a certain gap in our image geometric precision compared with the advanced level.Aiming at improving geometric precision of domestic high resolution optical satellites，some domestic satellite image geometric precision upgrading theory and methods are presented；by detecting and eliminating various kinds of error including equipment installation error，attitude and orbit measurement error，camera distortion，time synchronization errors and other errors in data processing flow，the geometric precision of satellite images has been significantly improved；some geometric precision improvement experiments are executed；via the proposed geometric processing，the geometric precision of theses satellite images can be improved to be better than 1.5pixel，which is higher than the designed accuracy of the satellite.

remote sensing；domestic optical satellite；geometric precision；precision improvement；parallel observation

P23

：ADOI：10.3969／j.issn.1673－8748.2016.01.001

2015－12－01；

：2016－01－08

国家自然科学基金（91538106，41501503，41201361，41501383），测绘地理信息公益性行业科研专项（201512022）

李德仁，男，中国科学院院士，中国工程院院士，武汉大学教授，博士生导师，著名摄影测量与遥感学家。曾任武汉测绘科技大学校长、中国测绘学会理事长。主要从事以遥感（RS）、全球卫星定位系统（GPS）和地理信息系统（GIS）为代表的空间信息科学与技术研究工作。Email：guozhang＠whu.edu.cn。