系泊多体海上平台非线性动力特性研究

李洪仙，陈衍茂，巫志文

(中山大学 工学院，广东 广州 510006)

系泊多体海上平台非线性动力特性研究

李洪仙，陈衍茂，巫志文

(中山大学 工学院，广东 广州 510006)

海上浮式平台通常由多个大型浮体模块柔性连接，组成一个典型的刚柔流耦合的多振子网络系统。本文从网络动力学角度研究多体浮式海上平台，通过龙格库塔法求解海上浮式平台运动微分方程，得到海洋平台运动响应随连接件刚度变化情况。数值结果表明，连接件刚度变化使得多体海上浮式平台表现出丰富的非线性动力特性现象，例如幅值跳跃、分岔、混沌等现象。为进一步揭示非线性浮式平台的集体动力学行为，作出浮块在各响应阶段对应的时域图和相图比较。本文得到的初步研究结果及研究方法，可为大型海上浮体结构初步设计提供理论参考。

海上浮式平台；网络动力学；龙格库塔法；非线性动力特性

0 引 言

海上浮式平台由多个模块拼接而成，可成为海上综合补给基地，具有燃料补给，飞机起降，后勤保障和旅游等功能，能用于维护国家深远海海洋权益。因此，国际海洋工程界掀起研究超大型浮式结构物的热潮，各国学者对超大型海洋浮式结构展开了大量的理论和应用研究。日本最早研究一种浮箱式海上平台，并通过试验验证海上浮动平台可行性[1-2]。相比于日本，美国提出半潜式的移动海上移动基地，并进行相关研究[3]。

在国内，从 20 世纪 90 年代起开始，吴有生和崔维成等也相继对超大型海洋结构物深入研究。吴有生和杜双兴[4]使用三维线性水弹性力学分析了极大型浮式结构物的运动和连接器的应力响应。闫红梅和崔维成[5]使用 Eatock Taylor 提出的一种矩形平板格林函数法分析了超大型浮体的水弹性响应。宋皓[6]对具有缓变地形的超大型浮体响应使用多重尺度法和常规的有限水深格林函数法势流理论进行了分析。Wu 和 Cui[7]对三维线性和非线性水弹性的发展以及试验技术进行了综述。徐道临[8]将网络动力学方法引入到海上浮动机场的动力学研究中，为海上多体系统研究提供一个新的视角和途径。

浮式海洋平台以其自身优势多运用于潮差较大的海域，将若干浮体模块通过柔性连接件相连，首尾两端锚索定位，组成一个典型的刚柔流耦合的多振子系统。将每个模块当做一个独立振子，引入 2 个相对独立的耦合参数来分别表示浮体间的吸引作用和排斥作用，它们之间的相互作用会产生很多丰富力学现象。本文研究吸引和排斥耦合共存的多体浮式海洋平台系统，探索 2 种竞争相互作用下海洋平台的非线性动力特性。

1 多体海上浮动平台建模

1.1 物理模型

超大型海上平台由 n 个浮体通过柔性连接件链式组合而成，平台首尾两端浮体有锚泊缆线约束，自由漂浮于水面上，如图1 所示。假设流体为不可压缩、无旋的理想流体；假设浮式平台为刚体，相邻浮体之间由柔性连接件连接，组成刚柔流耦合模型。

以静止水平面为 xoy 平面，x 轴与码头轴线平行，z 轴竖直向上且与平台轴线在同一竖直面内，波浪运动方向与 x 轴正方向一致，只考虑平台的纵荡和垂荡运动。坐标系定义以及模型示意图如图1 所示。

图1 多模块海上浮式平台的物理模型Fig. 1 Physicalmodel ofmulti-modules offshore floating platform

1.2 数学模型

由牛顿-欧拉动力学方程，可以推导出单个浮体在波浪上运动的动力学方程：

式中：i 为浮体编号；Mi为质量矩阵；μi为附加质量矩阵；λi为附加阻尼矩阵；ci为静水恢复力矩阵；Ki为系泊刚度矩阵；Xi为位移矩阵；Fwi为波浪力矩阵。

水动力系数 μi和 λi可通过水动力软件 AQWA 确定。静水恢复力系数 ci可以根据浮体质量分布与排水体积确定。根据浮体系泊约束情况，系泊刚度矩阵 Ki可以通过悬链线方程推导得到。由波浪入射势用时域哈斯金特关系确定波浪力 Fwi，其表达式为：

式中：φi为入射波作用于浮体 i 的初相位；fwiI为作用于浮体波浪力幅值，可由波浪理论决定。

式中：ρ 为水密度；g 为重力加速度；a 为波高；k 为波数；Li为浮体长度；Dw为水深；di为浮体吃水深度。

相邻浮体间通过柔性连接件相互连接，引入 2 个耦合参数 ε1和 ε2分别表示连接件对相邻浮体的橡胶排斥和缆绳吸引作用，ε1和 ε2相当于连接件的刚度系数，E1和 E2为形变函数，体现材料非线性。

橡胶只有受压作用，缆绳只有受拉作用，体现分段非线性，所以有

式中：δ 为浮体间初始间距；∆δ 为相邻两浮体中心总位移变化量；α 和 β 分别为缆绳在纵荡和垂荡的变化量。

在单浮体模型公式（1）的基础上，考虑连接件作用，可推导出多浮体计算模型：

其中a表征浮体之间连接关系，称之为拓扑结构矩阵。若相邻则为 1，否则为 0。另外，由于模型只有首尾两浮体有缆索系泊，所以只有首尾浮体运动方程中含有系泊刚度矩阵 Ki。

2 海上浮动平台非线性响应特性分析

2.1 数值算例

本文选取计算模型为五浮体海上平台，为了不失一般性考虑普通海域，浮体结构几何参数和海况参数如表1 所示。L 为浮体长度，H 为浮体的高度，d 为浮体吃水深度，δ 为相邻浮体的间距，Dw为水深，W 为波浪的波高幅值，T 为波浪的周期。

表1 浮体模块及海况参数Tab. 1 The size ofmodule and the parameters of sea

2.2 非线性响应

对于浮动海上平台非线性动力特性，比较关心的关键参数是连接件刚度变化如何影响系统动力响应。由于算例为对称结构，而m1和m5浮体锚固在波浪作用下运动响应较小，所以这里只考虑m2和m3浮体运动响应情况。图2～图5 对应 η（橡胶和缆绳刚度比值）为 0.5 的模块响应幅值图。

图2 和图3 分别是m2纵荡和垂荡响应幅值随缆绳刚度变化，从图可知：

1）M2模块响应幅值在缆绳刚度 0.12×105～0.21×105N/m区间出现跳跃现象，且纵荡跳跃的幅值较大而垂荡较小；

2）M2模块的纵荡和垂荡响应幅值在缆绳刚度 0.48×105～0.88×105N/m出现较大幅值振荡。这与非线性系统弯曲的共振支有关；

3）在缆绳刚度区间 0.88×105～2.2×105N/m，M2模块响应幅值先稳定变化，达到分岔临界点 1.4×105N/m后出现幅值分岔，接着达到大幅值振荡分界点后出现不稳定大幅值振荡区间；

4）整体看，随着缆绳刚度增加m2纵荡响应幅值呈现下降趋势，垂荡响应幅值呈现上升趋势，这是由于随着连接件刚度增加，纵荡方向的响应能量向垂荡方向转化。响应幅值的跳跃及大幅值振荡对海上平台自身稳定是非常不利的，所以在设计多浮体码头时，一定要选择合理的连接器刚度，避免出现响应阶跃的参数组合。

图4 和图5 是m3纵荡和垂荡响应幅值随缆绳刚度变化，其变化规律和m2模块响应大体一致，主要区别在于m3模块纵荡响应幅值在缆绳刚度区间 0.21×105～0.48×105N/m，0.88×105～1.4×105N/m和 2.2×105～2.5×105N/m出现小幅值分岔。为了进一步揭示海上平台的非线线性特性，下面将以m3模块的纵荡响应做具体分析。

图2 M2浮体纵荡响应幅值Fig. 2 Amplitude of surgemotions form2

图3 M2浮体垂荡响应幅值Fig. 3 Amplitude of heavemotions form2

图4 M3浮体纵荡响应幅值Fig. 4 Amplitude of surgemotions form3

图5 M3浮体垂荡响应幅值Fig. 5 Amplitude of heavemotions form3

2.3 时域分析

图6 和图7 分别是m3模块对应不同缆绳刚度的纵荡响应时程图和相图。从图6 可知，图6（a）和图6（c）是m3模块分别对应缆绳刚度 0.3×105N/m和 1.5×105N/m的纵荡响应时程图，具有周期性，且它们对应的图7（a）和图7（c）相图轨迹可以确定，它们属于周期运动。图6（b）是m3模块对应缆绳刚度 0.6×105N/m的纵荡响应时程图，不具有周期性，且它对应的图7（b）相图轨迹不能确定，属于混沌运动。

混沌运动是一种由确定性振动系统产生，对于初始条件极为敏感而具有内禀随机性和长期预测不可能性的往复非周期运动，所以从消振角度很难对海洋平台混动运动进行控制，所以对海上平台连接件设计时尽量避免刚度落在混动区域。从图6 和图7 可发现，混沌运动振幅比周期运动振幅还要大，因此海上平台安全设计时，应多考虑连接件刚度在振幅振幅稳定区域。

图6 M3纵荡响应Fig. 6 Surgemotions form3

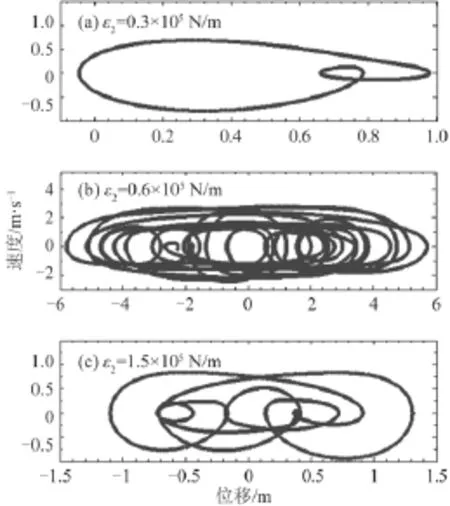
图7 M3纵荡响应相图Fig. 7 Phase diagramof heavemotions form3

3 结 语

规则波作用下，吸引和排斥耦合的相互作用使得多体海上平台表现出丰富的动力学现象。随着耦合子强度的改变，海上平台运动响应会出现幅值跳跃，分岔，混沌等现象。由于随着连接件刚度增加，纵荡方向的响应能量向垂荡方向转化，所以在连接件强度设计时，一定要选择合理的连接器刚度，充分发挥连接件的作用。混沌运动振幅比周期运动振幅还要大，因此海上平台安全设计时，应多考虑连接件刚度在振幅稳定区域。综上所述，在多体海上平台初步设计时，一定要考虑连接件的刚度选择，避免出现幅值跳跃的参数区间。

[1]KYOZUKA Y, KATO S, NAKAGAWA H.anumerical study on environmental impact assessment ofmega-float of Japan[J].marine Structures, 2001, 14(1/2): 147-161.

[2]SUZUKI H. Overview ofmegafloat: concept, design criteria, analysis, and design[J].marine Structures, 2005, 18(2): 111-132.

[3]BHATTACHARYA B, BASU R,mA K T. Developing target reliability for novel structures: the case of themobile off shore base[J].marine Structures, 2001, 14(1/2): 37-58.

[4]吴有生, 杜双兴. 极大型海洋浮体结构的流固耦合分析[J]. 舰船科学技术, 1995, 17(1): 1-9. WU You-sheng, DU Shuang-xing. Fluid-structure interaction analysis of very large floating structures[J]. Ship Science and Technology, 1995, 17(1): 1-9.

[5]闫红梅, 崔维成, 刘应中. 超大型浮体水弹性分析的平板格林函数法[J]. 海洋工程, 2003, 21(4): 8-14, 22. YAN Hong-mei, CUI Wei-cheng, LIU Ying-zhong. Hydroelastic analysis of VLFS using Plate Green Functionmethod[J]. The Ocean Engineering, 2003, 21(4): 8-14, 22.

[6]宋皓, 崔维成, 刘应中. 底部呈二维缓变情况下超大型浮体水弹性响应的两种计算方法比较[J]. 海洋工程, 2005, 23(4): 1-8. SONG Hao, CUI Wei-cheng, LIU Ying-zhong. Comparison of two numericalmethods for prediction of hydroelastic responses of VLFS on 2Dmild variable bottom[J]. The Ocean Engineering, 2005, 23(4): 1-8.

[7]WU Y S, CUI W C. Advances in the three-dimensional hydroelasticity of ships[J]. Proceedings of the Institution ofmechanical Engineers, Partm: Journal of Engineering for themaritime Environment, 2009, 223(3): 331-348.

[8]徐道临, 卢超, 张海成. 海上浮动机场动力学建模及非线性动力响应特性[J]. 力学学报, 2015, 47(2): 289-300. XU Dao-lin, LU Chao, ZHANG Hai-cheng. Dynamicmodeling and nonlinear characteristics of floating airport[J]. Chinese Journal of Theoretical and Appliedmechanics, 2015, 47(2): 289-300.

Nonlinear dynamic characteristics ofmooringmodules-offshore Platform

LI Hong-xian, CHEN Yan-mao, WU Zhi-wen

(College of Engineering, Sun Yat-sen University, Guangzhou 510006, China)

Offshore floating platformconsists ofmultiplemodules by flexible connectors. It isatypical dynamic network systemwith flexible-rigid-fluid coupling. This article researchesmodules-offshore Platformfromthe perspective of network dynamics. Solving the differential equation of platformmotion through the Runge-Kuttamethod and gettingmotion response of platformwith fitting stiffness change. In numerical simulation,modules-offshore platformshows the abundant nonlinear dynamic characteristics, for example, the jump of amplitude, bifurcation and chaos. In order to further reveal the collective dynamics behavior of floating platform,making time-domain diagramand phase diagrams to compare. Preliminary research results and researchmethods obtained in this paper can provideatheoretical reference for the design of very large floating structures.

offshore floating platform；network dynamics；Runge-Kuttamethod；nonlinear dynamic characteristics

P75

：A

1672 - 7619(2016)10 - 0052 - 04

10.3404/j.issn.1672-7619.2016.010.010

2016 - 03 - 15；

2016 - 04 - 25

国家自然科学基金资助项目(11572356，111272361)

李洪仙(1991 - )，男，硕士研究生，从事浮式结构网络系统非线性动力学研究。