浅议试题命制中浮体平衡的稳定性问题

唐建国

(苏州市胥江实验中学校 江苏 苏州 215004)

在初中物理教学中，有一类关于物体漂浮的习题比较常见，如以下例题：

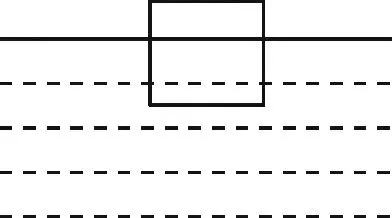
图1 例题题图

由于此类题目综合考察了二力平衡、阿基米德原理和密度的知识，因此广受试题命题者的青睐，甚至也常见于各地的中考试卷中.然而让命题者忽视的是，呈现给学生的示意图虽然符合二力平衡的条件，却没有考虑到漂浮的物体(以下称浮体)平衡时的稳定性[1].

考虑如图2(a)所示的一个对称浮体.在初始状态，浮体是平衡的，重心C在上，浮力F的作用点浮心D在下，通过CD的连线称为浮轴.当浮体受到微小的扰动，浮体发生等体积倾斜，即浮体排开液体体积不变，浮力的大小不变，但浮心移至D′点，如图2(b)所示.此时浮力作用线与浮轴的交点称为定倾中心，记作M点，当浮体偏转的角度θ较小时，可以认为定倾中心M点的位置不变.M点至D点的距离MD称为定倾半径，记作R.根据流体力学的知识，浮体的稳定性是由浮体的重心C和定倾中心M的相对位置决定的[2].

图2 对称浮体

(1)当重心C在定倾中心M之下时，浮力和重力组成一个扶正力矩，如图3(a)所示，使物体从偏斜位置恢复到原来的平衡状态，这种情况称为稳定平衡.

(2)当重心C和定倾中心M重合时，浮体在任何倾斜位置都能保持平衡，如图3(b)所示，这种情况称为随遇平衡.

(3)当重心C在定倾中心M之上时，浮力和重力组成一个倾覆力矩，如图3(c)所示，浮体无法从偏斜位置恢复到原来的平衡位置，这种情况称为不稳定平衡.

(a)

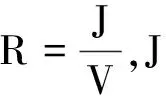
图4 长方体木块浮于水面

即为

又由于浮力和重力相等，所以

ρ木gBLH=ρ水gBLh

简化为

代入平衡稳定条件得

根据上式，教师在命制相关习题的时候，要考虑给出的已知物理量要符合浮体的平衡条件的约束.

(1)若木块是正方体(B=L=H)或者截面是正方形的长方体(L=H)，上式变为

6n(1-n)<1

整理得到：6n2-6n+1>0 解不等式得到

或

只有当n，也就是木块密度和水的密度的比值满足上述条件，呈现给学生的木块的平衡状态才能稳定.所以，本文一开始给出的题目，木块的密度与水的密度的比值为0.6，其显示的平衡状态是不稳定的，实际实验中这种平衡状态下的木块会很容易倾覆.

即

通过上述讨论，教师在命制此类题目时要考虑全面，浮体的平衡既要满足二力平衡的条件，也要符合平衡稳定性的约束，要让纸面上呈现给学生的条件、图能经得起实验的检验.