大型箱体零件结构拓扑优化设计研究

秦东晨，杜　鹏

(郑州大学 机械工程学院，河南 郑州 450001)



大型箱体零件结构拓扑优化设计研究

秦东晨，杜鹏

(郑州大学 机械工程学院，河南 郑州 450001)

摘要：大型箱体零件在机械设备中使用广泛，主要依靠传统经验设计而成，结构笨重.采用SIMP变密度法，以柔顺度最小化为目标，体积为约束，建立了大型箱体零件结构的拓扑优化数学模型.利用密度过滤和灰度过滤处理，解决了拓扑优化过程中数值不稳定问题.使用OC准则求解获得不同载荷工况下的拓扑结构，通过结构综合获得大型箱体零件新型结构，并用有限元方法验证该结构的可行性和实用性，为大型箱体零件的结构设计提供了一种有益的指导.

关键词：大型箱体零件；拓扑优化；变密度法；惩罚因子；过滤函数

0引言

大型箱体零件是指机械设备中体积、重量较大，内部有筋板布置，承受一定载荷的壳体结构零件，是装备制造业重要基础件之一，例如机床床身、桥式起重机主梁等.目前，大型箱体零件结构设计主要采用类比和经验等传统设计手段，零件结构笨重.拓扑优化能够进行结构大幅度减重设计和创新设计，许华旸[1]等对惯性载荷下的飞行模拟器大臂使用导重法进行拓扑优化研究，减轻了结构重量；刘书田[2]等对大口径空间光学反射镜的筋板位置进行拓扑优化，获得了合理的筋板布局.拓扑优化已经成为工程设计领域重要的研究课题.

大型箱体零件拓扑优化方面，雷少敏等[3]使用拓扑优化对多载荷工况下的铣床横梁筋板布局进行了研究；秦东晨[4]等对桥式起重机主梁进行了拓扑优化.研究较多采用商用有限元软件中的优化模块，拓扑优化过程难以进行精确控制和修改.

笔者通过已有程序使用拓扑优化理论深入研究大型箱体零件结构设计.根据受力将大型箱体零件抽象为简支梁，使用SIMP变密度法建立大型箱体零件优化模型，研究其求解存在的问题，分析载荷位置变化下的结构特征，最后综合成一个新大型箱体零件结构，并采用有限元方法验证该结构的可行性和实用性.

1变密度法(SIMP)

1.1基本思想

SIMP变密度法由Mlejnek等[5]在1993年提出，基本思想是假定存在一种密度可变的材料，在材料密度和材料弹性模量之间建立关系，以单元材料密度为设计变量，将拓扑优化问题转化为材料最优分布问题.SIMP变密度法通过下面公式建立材料密度和弹性模量之间的关系.

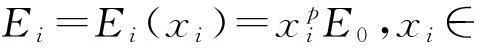
(1)

式中：E0为材料弹性模量；xi为第i块离散后单元体密度；p为惩罚因子.

1.2惩罚因子选择

变密度法中材料密度在0～1连续变化，优化后结构会存在密度为中间值的区域，这种区域无法加工，需要尽量抑制.惩罚因子p的作用是对设计变量中间密度值进行惩罚.根据公式(1)，假设材料弹性模量E0=2.0×105MPa，图1表示惩罚因子大小对弹性模量的影响：随着惩罚因子数值增大，中间密度向弹性模量区间两头靠拢，达到惩罚效果.

结构拓扑优化结果会受惩罚因子数值改变的影响.当惩罚因子p取值大于某值后，结构优化结果是错误的[6]，如图2.当p=5时简支梁优化模型趋向于杆状结构，不符合工程要求.因此，对于简支梁模型，惩罚因子取值为3较合适.

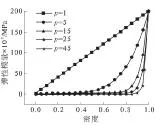
图1　惩罚因子作用

图2　不同惩罚因子对简支梁优化结果影响

2拓扑优化模型建立

简支梁使用有限单元法进行离散，每个离散单元都有一个密度xi，所有密度变量组成一个设计空间

X=[x1,x2,…,xi,…,xn]T.

(2)

式中：n为离散简支梁中单元数量.

对离散简支梁，使用整体柔顺度最小化为目标函数，体积为约束建立优化模型

minc(X)=FTU(X)

(3)

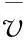
3灵敏度分析

对于优化模型，灵敏度分析是寻优过程必不可少的部分.其中体积偏导数如下

(4)

式中：vi为第i块单元体积.

体积约束灵敏度为每个单元的原始体积，在这里是一个常量.

由于载荷F与设计变量无关，对有限元公式

K(X)U(X)=F.

(5)

两边求偏导得到

(6)

目标函数两边偏导

(7)

将式(6)代入式(7)得到

(8)

根据有限元理论，整体刚度矩阵

(9)

对上式偏导

(10)

将式(10)代入式(8)，得到目标函数灵敏度

(11)

目标函数灵敏度可以在单元层面进行计算，减小了求解过程的复杂度.灵敏度分析也为寻优过程的迭代求解和数值过滤提供了基础.

4过滤函数

拓扑优化会产生数值不稳定现象，常见有棋盘格、网格依赖.如图3中简支梁模型，左图网格划分为100×20×4，右图网格划分为10×2×4.图3中模型没有使用数值过滤技术，两种网格划分后的优化结果出现了棋盘格，并且两者网格疏密不同产生的优化结构也不同，网格依赖使结构制造可能性和可靠性下降.

图3　数值不稳定现象

棋盘格和网格依赖一般同时出现，能抑制棋盘格的方法也能抑制网格依赖问题[7].一种常用抑制这些问题的方法是在优化过程中进行材料密度过滤[8].密度过滤使用下列函数

(12)

式中：Ni表示单元xi的相邻单元.

灰度过滤方法[9]是另一种常用方法.灰度过滤是一种非线性方法，是通过修改OC准则来实现的

(13)

式中：η是OC准则中的一个参数，代表数值阻尼系数，取0.3；q是灰度过滤参数，通常情况下q取2，当取值为1时就是经典OC准则.

不同过滤方法对拓扑优化结果有一定影响，如图4.与不使用过滤函数相比，使用过滤时棋盘格现象得到一定遏制，结构更加清晰；单独使用时密度过滤效果较好，而灰度过滤结果仍然出现棋盘格，因此灰度过滤不适合单独使用；联合使用两种过滤方法与单独使用密度过滤方法相比，两者结果有一定差别.鉴于过滤函数的作用分析，针对简支梁采用密度过滤、密度与灰度过滤联合两种方法进行优化.

图4　过滤方法对优化影响

5不同工况拓扑优化结构与分析

大型箱体零件根据几何形状和受力分析可以简化为空心简支梁模型.为凸显大型箱体零件内部结构布置，对大型箱体零件拓扑设计使用离散后的实心简支梁模型.

实心简支梁模型尺寸为10×1×1 m，材料为Q345，弹性模量为2.0×105MPa，泊松比为0.3，结构安全系数为1.4，材料许用应力为246 MPa，力跨中时许用挠度为12.5 mm.根据大型箱体零件支撑位置分析，简支梁底部左右两条边被约束.

对该简支梁在不同工况下使用不同过滤函数得到的结果如图5.其中左边一列使用密度过滤得到，右边一列使用密度过滤和灰度过滤联合方法得到；图中字母标号对应上述工况字母标号，每一行工况相同.

4种工况下两种不同过滤方法得到的结构具有一些共同特征.结构整体都呈现梯形形状，且可以分为两大部分：中间主体结构和左右两端支撑结构.由于简支梁上部承受载荷，模型中间主体部分呈现上宽下窄的梯形结构，并且前后腹板中心位置出现了较大的梯形孔洞.左右两端支撑结构的上下材料被去除.4种工况下上盖板位置没有出现孔洞.在同种工况的结构图中，深黑色部分布局基本相同.深黑色代表了受力较大的单元，是模型优化后的主体结构，可以在其位置加上筋板结构来增强结构强度.

2种过滤函数得到的结果也有不同特征.使用密度过滤后，4种工况模型下盖板消失，中间结构横截面变成倒U字形；而使用密度和灰度联合过滤后，下盖板存在，横截面是一个口字型.而且由于模型中加载的是竖直向下载荷，不存在其它方向分量，因此这两种截面结构稳定性都较好.但实际载荷工况中载荷会有横向分量，这时口字型结构稳定性较好.因此，下盖板的存在还是必要的.

6结构综合与分析

考虑到大型箱体零件通常为空心结构，根据上述优化结构的特征分析，在空心箱体的相应部位去除材料，得到大型箱体零件一个新结构，如图 6.

图5　不同工况不同过滤函数简支梁拓扑优化结果

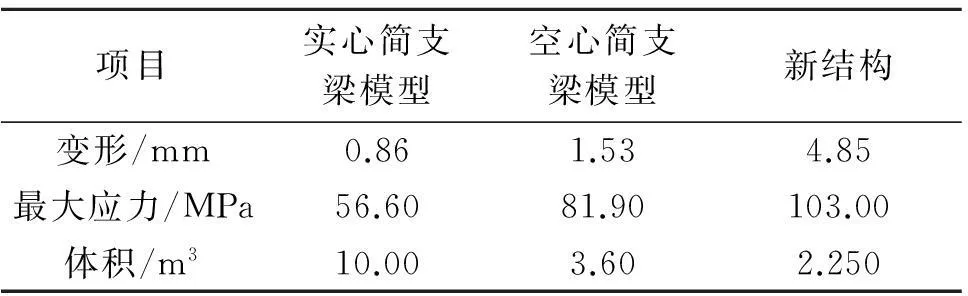
建立新结构有限元模型，获得其在不同工况下变形和应力，分析是否符合工程要求.同时建立实心简支梁和空心简支梁模型，3种模型对比分析得出载荷在简支梁中部时处于最危险工况.求解该工况下实心简支梁模型、空心简支梁模型和新结构的变形和应力，得到表1、图7、图8.3种模型最大变形依次增大，新结构变形最大，为4.85 mm，但在许用挠度12.5 mm内.应力方面，最大应力依次增大，新结构应力最大，为103 MPa，在许用应力246 MPa内，并且从应力图可以看出新结构应力较前两种模型更为均匀，符合拓扑优化材料利用率最大化思想.

新结构体积只有实心简支梁的22.5%，是空心简支梁的62.5%.在同等材料密度下，体积减少意味着结构重量减轻.这说明新结构大大减轻了重量， 同时在最危险工况下也能满足工程设计要求，因此新结构是具有可行性和实用性的.

图6　大型箱体零件新结构

项目实心简支梁模型空心简支梁模型新结构变形/mm0.861.534.85最大应力/MPa56.6081.90103.00体积/m310.003.602.250

图7　最危险工况变形图

图8　最危险工况应力图

7结论

(1)惩罚因子大小对优化结果有重要影响，且惩罚因子并不是越大越好，应该选取合适值.对于简支梁模型，惩罚因子选为3较合适.

(2)过滤函数种类不同会对结构产生一定的影响.对简支梁模型，灰度过滤单独使用效果不佳，而与密度过滤联合使用可以获得较优的拓扑结构.

(3)载荷作用位置不同会得到不同优化结构，优化结构中存在一些共同结构特征，可以用来指导大型箱体零件设计.

(4)新结构符合工程要求，是大型箱体零件拓扑优化设计的产物，为大型箱体零件结构设计提供了一种有益的指导.

参考文献：

[1]许华旸,关立文,王立平,等. 惯性载荷下飞行模拟器大臂结构的拓扑优化[J]. 机械工程学报, 2014, 50(9):14-23.

[2]刘书田,胡瑞,周平,等. 基于筋板式基结构的大口径空间反射镜构型设计的拓扑优化方法[J]. 光学精密工程, 2013, 21(7):1803-1810.

[3]雷少敏,唐华平,朱维南. 3ZX平面铣床横梁有限元分析及优化研究[J]. 郑州大学学报(工学版), 2011, 32(3):60-63.

[4]秦东晨,闫利利. 桥式起重机箱型主梁的结构优化设计[J]. 矿山机械, 2010, 38(12):48-51.

[5]MLEJNEK H P , SCHIRRMACHER R. An engineer's approach to optimal material distribution and shape finding[J]. Computer methods in applied mechanics and engineering, 1993, 106(1/2):1-26.

[6]陈祥,刘辛军. 基于RAMP插值模型结合导重法求解拓扑优化问题[J]. 中国机械工程, 2012, 48(1):135-140.

[7]左孔天,王书亭,陈立平,等. 拓扑优化中去除数值不稳定性的算法研究[J]. 机械科学与技术, 2005, 24(1):86-93.

[8]BRUNS T E, TORTORELLI D A. Topology optimization of non-linear elastic structures and compliant mechanisms[J]. Computer methods in applied mechanics and engineering, 2001, 190(26/27):3443-3459.

[9]GROENWOLD A A, ETMAN L F P. A simple heuristic for grayscale suppression in optimality criterion-based topology optimization[J]. Structural and multidisciplinary optimization, 2009, 39(2):217-225.

[10]AAGE N, ANDREASSEN E, LAZAROV B S. Topology optimization using PETSc: an easy-to-use, fully parallel, open source topology optimi-zation framework[J]. Structural and multidisciplinary optimization, 2015, 51(3):565-572.

[11]LIU K, TOVAR A. An efficient 3D topology optimization code written in Matlab[J]. Structural and multidisciplinary optimization, 2014, 50(6):1175-1196.

A Research for Structural Design of Large-scale Box Parts Based on Topology Optimization

QIN Dongchen, DU Peng

(School of Mechanical Engineering，Zhengzhou University，Zhengzhou 450001，China)

Abstract:The large-scale box parts are widely used in mechanical equipments. Because the design of large- scale box parts mainly rely on traditional experience, the structure is cumbersome. An optimization model to the large scale box parts, in which the compliance is minimized subjected to volume constraint, is established based on SIMP method. And the density filter and the gray scale filter are used to avoid the numerical instabilities that will occur in the optimization process. After loading the load in different positions of the large scale box parts respectively and using OC criteria to solve each condition, the optimal structures are obtained. Then, an optimal topology configuration is obtained by combining different optimal structures above, and its validity and practicability are tested by FEM. This research provides a useful guide for the design of the large scale box parts.

Key words:large scale box part; topology optimization; SIMP; penalization power; filter function

中图分类号：TH122

文献标志码：A

doi:10.3969/j.issn.1671-6833.201505028

作者简介:秦东晨(1965—)，男，河南温县人，郑州大学教授，博士，主要从事机械强度及结构优化设计、虚拟样机、CAD/CAE/CAM集成等研究，E-mail：dcqin@zzu.edu.cn.

基金项目：2015年度国家科技支撑计划资助项目(2015BAF06B06)

收稿日期:2015-05-19；

修订日期：2015-09-01

文章编号:1671-6833(2016)02-0082-05

引用本文：秦东晨，杜鹏.大型箱体零件结构拓扑优化设计研究[J].郑州大学学报(工学版)，2016,37(2):82-86．