多目标进化算法及其在电力环境经济调度中的应用综述

肖俊明，周　谦，瞿博阳，韦学辉

(中原工学院 电子信息学院，河南 郑州450007)



多目标进化算法及其在电力环境经济调度中的应用综述

肖俊明，周谦，瞿博阳，韦学辉

(中原工学院 电子信息学院，河南 郑州450007)

摘要：电力系统能源供应对现代社会至关重要，而电力系统环境经济调度问题的科学、有效解决是实现能源供应的保障.多目标进化算法在求解电力系统环境经济调度问题方面具有独特的优势.本文按时间顺序首先对多目标进化算法做了介绍，其次对多目标进化算法在电力系统环境经济调度问题中的应用进行了讨论，总结了近年来科学工作者的研究内容，并对此领域以后可能的发展方向进行了展望.

关键词：多目标优化；多目标进化算法；电力系统运行调度；经济环境调度

0引言

优化问题的求解过程是指通过特定方法获得目标函数的最优解,实际生活中许多问题都可视为优化问题.当优化的目标函数为一个时，称为单目标优化；当优化的目标函数有两个或两个以上时，称为多目标优化.多目标优化问题的解是由一组帕累托(Pareto)最优解组成的集合,集合中的各个元素称为Pareto最优解或非劣最优解[1].

起初,对于优化问题的求解有：线性规划、非线性规划、非线性方程组等求解方法.由于进化算法(evolutionary algorithms，EA)可处理非线性且非凸的优化问题，并且对具体问题的要求较少，因此被广泛的运用到工程、生物学、金融、社会科学等领域[2-3].EA之所以非常适合于解决多目标优化问题是因为它不仅具有很强的鲁棒性，而且它可以在一次运行中产生多个最优解.多目标进化算法(multi-objective evolutionary algorithms，MOEA)是在EA基础上发展而来的用于解决多目标优化问题的算法.从上世纪90年代中后期起，MOEA一直是进化计算领域研究热点之一[4-7].

电力系统能源供应对社会发展至关重要，现今社会对能源供应的依赖愈加强烈.如何运用科学有效的技术和方法解决电力系统运行的调度问题引起了国内外学者的关注[8-10].电力系统运行调度问题是指保证系统安全稳定和电能质量满足标准的条件下，最大限度地提高电力生产和传输效率，降低燃料消耗以及供电成本，其本质为复杂的优化问题.早期，电力系统的调度问题主要集中在机组组合及启停(unit commitment，UC)的优化问题上，其目的为确定各机组在某一调度周期中各时段上的运行状态.常规的调度问题一般采用系统运行成本最小作为优化目标[11]，却忽略了能源消耗对环境和社会可持续发展的负面影响.

全球环境问题日益严峻，保护生态环境已成为全人类的共识.环境经济调度(environmental economic dispatching，EED)受到了广泛关注,仅需对现有调度策略稍做修改，就能兼顾环保和经济两个因素，EED问题是一个非线性、非凸的多目标优化问题.对于EED问题，早期的解决是利用约束条件法或加权系数法等方法将多目标问题转化为单目标问题，然后利用传统的优化方法进行求解，每次仅能得到一种权重情况下的最优解，且权值对结果的影响较大，计算结果难以令人满意[12].近年来，由于启发式优化算法在解决多目标问题时的突出表现，针对EED问题的研究逐渐转向利用多目标进化算法来获得更科学、合理的调度方案.

1多目标进化算法

1.1多目标优化问题及其数学描述

多目标优化问题是指在满足一定约束条件下，同时求解一组目标之间相互冲突的最大或者最小值的问题.

多目标优化问题的数学描述如下：

min:y=(f1(x),…,fm(x)),m=2,3，…,M

(1)

式中：x为D维决策变量；y为目标函数；M为优化目标总数；fm(x)为第m个子目标函数；g(x)与h(x)分别为不等式和等式约束条件；XiL和XiU为向量搜索的上、下限.

1.2典型的多目标进化算法

1.2.1基于GA的多目标算法

(1)矢量评价遗传算法(VEGA).矢量评价遗传算法(VEGA)由SCHAFFER于1984年提出[13]，该算法首次实现了遗传算法与多目标优化问题的结合.该算法针对每一个目标产生一个子种群，在每一代进化过程中个体的评价机制仅限于本种群内，而不考虑其他目标，个体的选择采用轮盘赌机制.

(2)多目标遗传算法(MOGA).1993年，FONSECA和FLEMING提出MOGA[14]，该算法在每一代进化中，对每个个体划分等级,非支配个体的等级为1，其它个体等级为支配该个体的数目加1，每一个个体的适应度值采用插值法分配.

(3)基于小生境帕累托遗传算法(NPGA, NPGA-II).NPGA是小生境算法与GA思想相结合的产物[15].其优点是可适用于大多数的多目标优化问题.2001年，ERICKSON等人提出了NPGA-II[16].该算法运用轮盘赌选择机制，采用小生境技术选取进入下一代的个体.

(4)非支配排序遗传算法(NSGA, NSGA-II).1994年，SRINIVAS和DEB基于Goldberg的非支配思想提出NSGA[17]，非支配思想的目的就是将进化过程中的个体配置在全部帕累托最优解空间，实现解的多样性.2002年，DEB等人在NSGA算法的基础上提出NSGA-II[18].相比于NSGA，NSGA-II的优点包括：①提出快速非支配排序算法，降低了计算的复杂度；②采用精英策略，保证优良的个体在进化过程中不会被丢弃，从而提高了优化结果的精度；③采用拥挤度比较算子，保证种群的多样性.

1.2.2基于DE的多目标算法

1995年,文献[19]为解决无约束单目标优化问题提出了差分进化(differential evolution，DE)算法，DE操作流程与遗传算法相同：变异、交叉和选择.DE中变异部分采用所选择变异个体之间加权差分向量产生新个体.2003年，XUE等人基于非支配概念提出多目标差分算法(MODE)[20]，该算法在变异部分加入扰动分项，扰动的大小随进化代数的增大而减小，从而加强对局部最优解的搜寻.为了解决差分算法中两个参数F、CR不易选择的问题，2009年，WANG等人提出多目标自适应差分算法(MOSADE)解决多目标优化问题[21].算法中DE两参数F、CR采用自适应的方法在预先设定的范围内取值.

1.2.3基于PSO的多目标算法

粒子群优化算法是1995年由KENNEDY和EBERHART受自然界中鸟群、鱼群等的启发提出的启发式智能优化算法.在将PSO拓展为多目标优化的过程中，如何运用全局和局部最优粒子来指导整个粒子群的搜索是关键问题.2004年，COELLO等人提出了多目标粒子群算法(MOPSO)[22]，该算法引入了自适应网格机制，变异部分不仅包含当前粒子群个体的搜索信息，还加入了变量范围因素，以此加强对整个变量范围内解的搜索.2007年，TRIPATHI等人提出时变的多目标粒子群优化算法(TV-MOPSO)[23],算法中两个重要参数惯性因子和加速系数均随着迭代代数自适应变化.将进化过程中搜索到的非支配解经过轮盘赌的方式进行选择，以此作为全局最优的粒子群更新方法，并且提出基于最近邻域的多样性参数，该参数值作为粒子个体的适应度值.

1.2.4基于人工免疫系统的多目标算法

人工免疫系统是受免疫学启发，模拟免疫学功能解决复杂优化问题的算法.免疫学与人工智能有密切联系，是人工智能方法灵感的重要源泉.2004年，COELLO等人提出多目标免疫系统算法(MISA)[24]，该算法采用帕累托支配概念、自适应网格机制来维持外部集合中的个体数量，并且对父代个体运用两种不同的变异策略.2008年，GONG等人提出非支配邻域免疫算法(NNIA)[25]，NNIA采用一种基于非支配概念的个体选择方法, 根据个体的拥挤程度进行比例克隆复制,随后运用新的重组、变异操作方法, 以此加强对当前Pareto前沿面中较稀疏区域的搜索，该算法在求解高维多目标优化问题方面具有良好的性能.

1.2.5基于MOEA/D的多目标算法

ZHANG等在2007年将数学规划方法和进化算法结合起来，提出了基于分解的多目标进化算法[26].该算法将整个Pareto最优前沿的逼近问题分解为一定数量的单目标优化问题，然后用进化算法同时求解这些子问题.

1.2.6其它多目标算法

除了上述的多目标优化算法之外还有许多，其中强度帕累托进化算法(SPEA、SPEA-II)在电力系统调度方面的应用较多，因此仅对二者进行介绍.SPEA是由ZITZLER与THIELE在1999年提出[27]，SPEA采用外部档案来存储每一代产生的非支配解，称为非支配解集，当外部种群的个体数目超过设定值时, 则用聚类技术来删减个体.ZITZLER等人于2001提出SPEA的改进版本—SPEA-II[28]，在SPEA的基础上对适应度分配、个体搜索方向以及外部集合的更新方法等3方面进行改进.

2多目标进化算法在电力环境经济调度(EED)中的应用

早在1994年，TALAQ等人提出同时考虑经济/环境的优化策略[29]：①将污染物(NOx、SOx等)排放量最小作为优化目标，将成本作为约束条件；②将成本最小作为优化目标，将污染物排放量作为约束条件；③将污染物排放与成本的加权和作为优化目标等策略.该方法虽然同时考虑了经济与环境因素，但未能给出二者在不同权重下的调度方案.近年来，国内外学者将MOEA应用于电力系统环境经济调度问题中，取得了很多有价值的成果，充分体现MOEAs在电力系统调度领域中的巨大潜力[30].传统EED问题的主流解决思路如下：在满足系统负荷要求与一定的约束条件下，将提供决策方案所需要的费用成本、污染物排放量作为优化目标，采用MOEAs进行求解.其数学模型如下所示.

(1)优化目标

①燃料费用[31]：

(2)

式中：N为系统中火电机组的台数；ai、bi、ci分别为火电机组i的运行费用系数；Pgi为第i台火电机组的有功出力.

②污染排放量[31]：

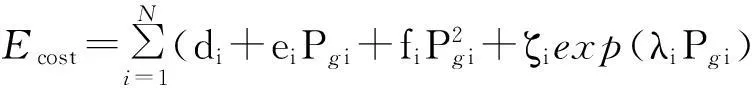
(3)

式中：di、ei、fi、λi、ζi分别为火电机组i的污染气体排放系数.以上为两种典型的优化目标，除此之外还可将有功功率损失[32]、系统运行风险[33]等作为优化目标.

(2)约束条件

①系统功率平衡约束如式(4)所示，式中PD为负荷有功功率；Ploss为系统网损[31].

(4)

②机组出力约束[31]

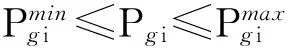
(5)

式中：Pgimin、Pgimax为第i台机组的最小和最大出力.

③支路传输功率约束[31]

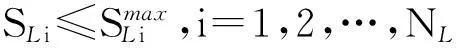
(6)

式中：SLi、SLimax分别代表线路i的传输功率及其上限；NL为线路条数.除以上几种约束外，还有机组爬坡速率、机组运行禁止区间以及正、负旋转备用容量等[34]约束条件.

2.1MOEAs在传统的EED问题中的应用

由于早期MOEA在耗时与应用方面的限制，1997年SRINIVASAN等人提出采用一种混合启发式进化算法对多目标EED问题进行求解[30]，从而提高解的可行性并减少计算时间.

2003年ABIDO提出将NPGA运用于多目标 EED问题[35]，采用模糊隶属度函数得到最优折中解.随后ABIDO又分别将NSGA[36]、SPEA[37]用于解决同一问题，对于现实约束方面，文献[36-37]均加入传输线路的安全性约束.作者通过采取多样性保持机制、分类聚集等机制获得了更加广泛的帕累托解集.

同年，HARRY将带有精英保留策略的NSGA-II用于解决EED问题[38].在考虑传输功率损失情况下，满足功率平衡、发电机输出功率等约束条件下进行求解，并将该方法分别在三发电机组系统下与禁忌搜索算法、六发电机组系统与模糊控制遗传算法(FCGA)作比较.结果表明带有精英保留策略的NSGA-II具有较快的求解速度.

2004年ZHANG等人提出了一种模糊多目标遗传算法(FMOGA)[32]，采用三目标机制来解决EED问题，目标分别是：燃料成本、污染物排放量、总有功功率损失，并采用模糊评价因子对适应度进行调整，一方面保证获得结果的多样性，另一方面可以消除不同目标值的边界差异对结果的影响.同年ZHAO等人同样运用以上3种目标采用MOPSO进行求解[39]，该文章中加入了多样性保护与加强全局搜索能力机制以提高解的质量.

2005年,在文献[38]基础上再次运用NSGA-II解决EED问题[40]，在随机与确定两种方法下进行求解.在确定问题的情况下分为两种策略:忽略系统功率损失和考虑功率损失.在随机方法下，考虑功率损失的同时又分为3种子情况：①各个发电机输出功率在给定平均值情况下随机变化，系统负荷固定；②各个发电机输出功率与系统负荷均在给定平均值情况下随机变化；③各个发电机输出功率、系统负荷以及污染物排放系数均在给定平均值情况下随机变化.作者详细分析了电力系统调度问题成本、排污量的实际值超过计划值的原因，给操作者提供更精确的决策依据.

2006年ABIDO同时将3种多目标进化算法NSGA，NPGA与SPEA用于解决电力系统调度问题[41]，并且提出一种评价多目标算法性能的标准，该标准包括3方面内容：①算法所得到非支配解与帕累托最优前沿间的距离越小越好；②所得到解应具有好的分布性；③非支配解的范围应尽量广，该标准为后期不同算法间的评价提供了衡量指标.同年GUESMI等人为解决EED的耗时问题[31]，提出了两步走的策略，首先采用NSGA-II对不同负荷条件下的调度问题进行求解，其次借用第一步的结果采用神经网络的方法得到调度决策，最后对该方法的有效性进行了验证.

2008年VENKATESH等人提出EED问题的2个新提法[42]：①经济环境的联合调度问题(combined economic emission dispatch ，CEED)为一个双目标优化问题，分别为成本与NOx排放量；②经济环境调度问题(economic emission dispatch ，EED)为一个3目标优化问题，分别为成本、NOx以及SO2排放量.作者采用MOEP分别对以上问题进行求解并与NSGA-II进行比较.结果表明：该算法在解决以上2问题时具有良好性能，可获得分布广泛、准确的帕累托前沿.AGRAWAL等人提出基于模糊聚类的粒子群算法(FCPSO)[43]，该算法中加入自适应变异、模糊聚类、多样性保持等机制来获得更加广泛、均匀的帕累托前沿.

2009年SUN等人针对电力公司提出一种3目标的优化调度方法[33].3目标分别为：系统运行风险、利润(成本中将电机的启、停费用考虑在内)、排污量.采用多目标非支配排序差分算法(NSDE)进行求解并与NSGA-II进行比较.该算法实现了非支配排序与差分算法的结合，并且对个体的拥挤距离机制与变异操作进行了改进，避免了算法的早熟与搜索不均，结果表明NSDE具有较好的收敛速度与求解精度.

2010年CAI等人提出多目标混沌蚁群算法(MOCASO)[44]，该算法采用Pareto支配解决多目标优化问题，运用模糊理论、适应度共享机制以及扰动因子提高算法性能.WU等人采用与文献[32]相同的3目标策略，运用MODE解决EED问题[45].文章中引入精英保留策略、基于熵的拥挤度计算等方法,实现了拥挤度的更准确计算，从而在一定程度上提高了算法的性能.

对于EED优化问题，BASU采用MODE进行解决[46].SIVASUBRAMANI提出采用一种新的多目标和声搜索算法(MOHS)进行求解[47]；PANIGRAHI等采用多目标细菌觅食算法(MOBF)对问题进行解答[48].

2012年ZHANG等人针对EED问题采取一种改进MOPSO的BB-MOPSO(bare-bones multi-objective particle swarm optimization)算法[49]，该算法将BB-PSO拓展至多目标优化问题，并将结果通过空间矩阵(spacing metric)以及二集合覆盖度(two-set coverage)与其它多种多目标算法进行对比.结果表明：通过种群更新以及变异等策略上的改进，算法的搜索能力与稳定性都有相应提高.NIKNAM等人提出一种增强的萤火虫群(EFA)算法针对热、电混合系统的EED问题进行求解[50]，算法中加入自适应概率的变异策略以及智能种群数量的方法，并在4种不同的情形下与萤火虫算法(FA)、增强萤火虫算法(EFA)等对比来验证其有效性.

2013年GHASEMI提出一种改进的多目标交互蜂群杂交算法(IHBMO)[51]，采用成本、污染排放和功率损失3目标优化策略，考虑发电机组阀点效应情况下，在IEEE-30/118系统与MODE、MOPSO等进行比较，结果表明：算法的搜索能力得到显著增强.AFZALAN与JOORABIAN提出一种新的占优多目标遗传算法(εv-MOGA)[34].在包含频率偏差、功率损失、有功功率限制、以及发电机禁止区间等更加切合实际情况的约束条件下，采取燃料、备用容量成本以及污染排放量为目标的两目标优化方法进行求解.NIKNAM等人采用一种分种群的差分算法解决EED问题[52].该算法分为3个阶段，各阶段进化代数均为最大进化代数的1/3，首先各种群之间独立进化，其次是种群之间互相交流阶段，最后是各种群合并一致进化阶段.

2015年WU等人提出一种有效的协同多目标粒子群进化(efficient co-evolutionary multi-objective particle swarm optimizer , ECMPSO)算法[53]，该算法在PSO的基础上加入动态蜂群技术、三级更新策略以及外部档案集合的跳跃策略以提高解的性能.在解决EED问题上与多目标人工蜂群算法(MOABC)、多目标综合学习粒子群优化算法(MOCLPSO)和采用差分策略的基于分解的多目标进化算法(MOEA/D-DE)进行对比.

由于电力系统的重要性，近年来对传统EED问题研究也相对较多，但解决EED问题时的优化目标不尽相同.大多采用成本与污染物排放作为双目标优化问题进行求解，但也包含有功功率损失最小或者风险最小等的3目标优化思路；约束条件也由系统功率平衡、机组出力约束等基本约束转向包含禁行区间、有功功率、无功功率、功率传输损失、备用旋转容量等更切合实际的约束；对多目标优化问题，算法更新策略方面也由起初的帕累托支配转向非支配排序、基于分解的方法.为了提高解的准确性，动态自适应机制、模糊理论、基于熵的拥挤度计算等方法也不断引入.

2.2MOEAs在包含新能源EED问题中的应用

随着环保意识加强以及科学的发展，包含风能、太阳能等可再生绿色能源的调度策略显得愈加有意义[54].风、光等清洁能源的接入无疑加大了电力系统调度问题的难度.

2006年WANG等人将风能作为能源之一[55]，采用MOPSO算法，提出了一种包含风能的风险定量方法，首先将风险与成本作为优化目标来解决EED 问题，并分析了不同容量的风电接入情况之间的对比，其次运用了包含风险、成本与污染物排放的3目标优化策略.

2009年BRINI等人将风能、太阳能、发电机组作为能源采用SPEA算法对EED问题进行求解[56]，并借助神经网络在一定程度上实现实时电力系统调度.

2010年，KUO将风能、发电机组为优化对象[57]，采用成本与污染物排放双目标优化对EED问题进行求解.文章采用新编码技术的SPEA算法实现了大功率风能接入情况下的优化调度，且在约束条件中加入了发电机的禁止运行区间、发电机爬坡速率限制等约束条件.

2014年MAN-IM等人针对含有风电接入的EED问题提出采用非支配排序的粒子群优化(NSPSO)算法进行解决[58].将风险与成本作为优化目标，在成本中加入风电预测误差惩罚部分，充分考虑了风电接入对系统安全性的影响.ZHU等人采用MOEA/D算法针对含有风电场的EED问题进行求解[59].作者采用基于多目标机会约束规划，建立含风电场EED的随机优化模型，并利用风电出力的分布函数对模型进行确定性转化，并在标准测试系统上与NSGA-II、MODE、模糊化多目标粒子群算法(FMOEP)的优化结果进行对比.结果表明MOEA/D算法对于带约束的EED问题可以获得较好的调度方案.

同年DECKMYN等人针对含有柴油发电机、燃料电池、光伏电池、风机的微网DEED问题[60]，提出了一种满足系统负荷要求的经济/环境实时调度方案.该方案采用多目标遗传算法进行求解，并通过具体的实例作为研究对象，验证所提方案的有效性.ADHVARYYU等人采用了一种新的仿生虾群(krill herd，KH)算法解决含有风电的热、电混合供电系统调度问题[61].

2.3MOEAs在动态EED问题中的应用

在电力系统调度优化问题中，由于电力系统负荷的变化性，动态环境经济调度(dynamic economic emission dispatch ,DEED)也逐渐成为了研究的热点[62].

2007年BASU提出一种基于模糊满意度的进化算法[63]，将DEED问题视为成本与排污量两目标优化问题，该方法可以根据不同的运行状况为决策者提供更科学、合理的方案.同年，DEB等人提出采用基于两种策略(DNSGA-II-A, DNSGA-II-B)改进的NSGA-II[64]算法解决DEED问题，假设负荷变化后在算法运行一代的时间内保持不变，所提出方法在一定程度上可解决实时的DEED问题.

2008年BASU提出运用NSGA-II解决DEED问题，详细给出了十机组发电系统24 h的调度计划[65].

2011年LEE等提出量子遗传算法(QGA)解决带有阀点、禁行区间因素的DEED问题[66]，作者在传统发电机的基础上加入了风电能源，并分别在不同真实场景下与进化规划(EP)、遗传算法(GA)等方法进行比较.结果表明所提算法可以实现实时解决DEED问题，具有良好的实用性.ABARGHOOEE等人在解决DEED问题时[67]，针对加入风能的随机性问题，提出基于风电预测的多目标优化，采用基于模糊满意度的PSO算法进行求解.

2013年BAHMAN等人提出一种新的模糊自适应学习粒子群算法(FALPSO)[68]，针对含有风电场的DEED问题进行求解.FALPSO算法中加入模糊自适应方法、模糊自适应更新策略等方法，作者采用随机规划的模型来解决风电场的随机性.

3结论

近年来，针对电力系统运行调度问题，学者们做出了更切合实际的研究：①根据电网运时的污染因素，采取环境保护调度；②根据电网负荷情况，采取稳定约束调度;③根据电网传输需求，采取实时以及运转备用容量调度；④考虑电网新能源接入，采取基于预测的机会约束规划机制；⑤根据多电网的调度范围以及用户的特殊需求，制定跨区域以及针对供、需求双方的调度新策略；⑥根据地域环境，制定了包含可再生能源的多种独立分布式电源调度策略.

随着电网的不断发展，电网容量也不断增加，用户对电能质量的要求也越来越高，在满足电网安全运行的情况下，除了经济、环境因素外，电网运行时的质量问题也亟待解决；电力系统问题从成本、环境的双目标优化发展为包含功率损失、风险以及稳定性等提高供电质量的多目标优化，在不断加入符合现实条件的约束同时，引入了新能源，这些使得电力系统调度问题变得愈加复杂.

多目标进化算法由于其在电力、金融、工业设计等诸多领域的广泛应用，得到了更为快速的发展.从二十世纪九十年代VEGA首次实际运用，到现如今各种具有优越性能的MOEAs算法不断出现，使得需要同时满足多个系统目标要求，且附带大量约束条件的电力系统问题得到了更为智能、科学的解决.加入风、光等新能源的EED、DEED问题，由于风、光电能受地理位置、环境因素以及实时性的影响较大，如何解决风、光电源以及DEED的不确定性是现如今科学工作者研究的关键，考虑供需双方共同决策的跨地域智能调度问题有待进一步的研究.

参考文献：

[1]肖晓伟,肖迪,林锦国,等.多目标优化问题的研究概述[J].计算机应用研究,2011, 28(3): 805-808.

[2]GAMARRA C, GUERRERO J M. Computational optimization techniques applied to microgrids planning: A review [J]. Renewable and sustainable energy reviews, 2015(48):413-424.

[3]LIANG J, QU BY, Large-scale portfolio optimization using multi-objective dynamic mutli-swarm particle swarm optimizer[C]// IEEE Symposium on swarm intelligence. Singapore: IEEE, 2013:1-6.

[4]ZITZLER E, DEB K. Comparison of multiobjective evolutionary algorithms: empirical results [J]. Evolutionary computation, 2000,8(2): 173-195.

[5]QU BY, SUGANTHAN P N. Multi-objective evolutionary algorithms based on the summation of normalized objectives and diversified selection [J], Information sciences, 2010, 180(17): 3170-3181.

[6]王欣,秦斌,阳春华,等.基于混沌遗传混合优化算法的短期负荷环境和经济调度[J]．中国电机工程学报，2006,26(11):128-133.

[7]张春江,CHEN T K,高亮,等.基于分解的多目标进化算法在工程优化中的应用[J].郑州大学学报(工学版), 2015, 36(6): 38-46.

[8]王振浩,李文文,陈继开,等.基于改进自适应遗传算法的分布式电源优化配置[J].电测与仪表, 2015, 52(5): 30-34.

[9]BERIZZI A, BOVO C, INNORTA M, et al. Multiobjective optimization techniques applied to modern power systems[C]// IEEE power engineering society winter meeting. Columbus: IEEE, 2001, 3:1503-1508.

[10]MOUSA A A, KOTB K A. A hybrid optimization technique coupling an evolutionary and a local search algorithm for economic emission load dispatch problem [J]. Applied mathematics, 2011, 2(7):890-898.

[11]ONGSAKU W, PETCHARAKS N. Unit commitment by enhanced adaptive lagrangian relaxation [J]. IEEE trans on power systems, 2004,19(1):620-628.

[12]朱永胜,王杰,瞿博阳,等. 采用基于分解的多目标进化算法的电力环境经济调度[J]. 电网技术,2014, 38(6): 1577-1584.

[13]SCHAFFER J D. Multiple objective optimization with vector evaluated genetic algorithms[C]//In Proceedings of the first International Conference on Genetic Algorithms. Hillsdale, NJ: Lawrence Erlbaum, 1985:93-100.

[14]FONSECA C M C, FLEMING P J. Genetic algorithms for multiobjective optimization: formulation, discussion and generalization[C]//The 5th international conference on genetic algorithms, San Mateo, CA: Morgan Kauffman , 1993: 416-423.

[15]HORN J, NAFPLIOTIS N, GOLDBERG D E. A niched Pareto genetic algorithm for multiobjective optimization[C]//Proceedings of the first IEEE conference on evolutionary computation. Orlando, FL: Evolutionary Computation, 1994:82-87.

[16]ERICKSON M, MAER A, HORN J. The niched pareto genetic algorithm 2 applied to the design of groundwater remediation systems[C]//International conference on evolutionary multi-criterion optimization, Lecture notes in computer science, Berlin: Springer, 2001:681-695.

[17]SRINIVAS N, DEB K. Multi-objective optimization using non-dominated sorting in genetic algorithms [J]. Evolutionary computation, 1994, 2(3), 221-248.

[18]DEB K, PRATAB A, AGARWAL S, et al. A fast elitist non-dominated sorting genetic algorithm for multi-objective optimization: NSGA-II[C]//The 6th international conference, Paris : Springer Berlin Heidelberg ,2000:849-858.

[19]STORN R, PRICE K. Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces [J]. Journal of global optimization, 1995, 11(4):341-359.

[20]XUE F, SANDERSON A C, GRAVES R J. Pareto-based multi-objective differential evolution [C]//Proceedings of the 2003 congress on evolutionary computation. Piscataway, NJ: IEEE, 2003: 862-869.

[21]WANG Y N, WU L H, YUAN X F,Multi-objective self-adaptive differential evolution with elitist archive and crowding entropy-based diversity measure [J], Soft computing, 2010,14 (3) : 193-209.

[22]COELLO C A , PULIDO G T, LECHUGA M S. Handling multiple objectives with particle swarm optimization [J]. IEEE transactions on evolutionary computation, 2004, 8(3):256-279.

[23]TRIPATHI P K , BANDYOPADHYAY S, Pal S K, Multi-objective particle swarm optimization with time variant inertia and acceleration coefficients [J], Information sciences, 2007,177 (22) :5033-5049.

[24]COELLO COELLO C A,CORETES N C. Solving multi-objective optimization problems using an artificial immune system [J]. Genetic programming and evolvable machines, 2005, 6(2):163-190.

[25]GONG M G, JIAO L C, DU H F, et al. Multi-objective immune algorithm with nondominated neighbor-based selection [J]. Evolutionary computation, 2008, 16(2):225-255.

[26]ZHANG Q F, Li H. MOEA/D: a multiobjective evolutionary algorithm based on decomposition[J]．IEEE transactions on evolutionary computation, 2007 ,11(6) :712-731.

[27]ZITZLER E, THIELE L. Multiobjective evolutionary algorithms: A comparative case study and the strength Pareto approach [J]. IEEE transactions on evolutionary computation, 1999, 3(4), 257-271.

[28]ZITZLER E, LAUMANNS, M, THIELE L. SPEA2: Improving the strength pareto evolutionary algorithm[R], Tech. rep., Computer Engineering and Networks Laboratory (TIK), Swiss Federal Institute of Technology Zurich , 2001:95-100.

[29]TALAQ J H, FERIAL, El-HAWARY M E. A summary of environmental/economic dispatch algorithms [J].IEEE transactions on evolutionary computation, 1994,9(3):1508-1516．

[30]SRINIVASAN D, TETTAMANZI A G B. An evolutionary algorithm for evaluation of emission compliance options in view of the Clean Air Act Amendments [J]. IEEE transactions on power systems, 1997, 12(1):336-341.

[31]GUESMI T, ABDALLAH H H, TOUMI A. New approach to solve multiobjective environmental/economic dispatch [J]. Journal of electrical systems, 2006, 2(2):64-81.

[32]ZHANG P X, ZHAO B, CAO Y J, et al. A novel multi-objective genetic algorithm for economic power dispatch[C]//39th International universities power engineering conference, Bristol, UK: IEEE, 2004, 1: 422-426.

[33]SUN H J, PENG C H, GUO J F, et al. Non-dominated sorting differential evolution algorithm for multi-objective optimal integrated generation bidding and scheduling[C]//IEEE international conference on ICIS, Shanghai: IEEE, 2009:372-376.

[34]AFZALAN E, JOORABIN M. Emission, Reserve and economic load dispatch problem with non-smooth and non-convex cost functions using epsilon-multi-objective genetic algorithm variable [J]. Electrical power & energy systems, 2013, 52(11):55-67.

[35]ABIDO M A. A niched Pareto genetic algorithm for multiobjective environmental/economic dispatch [J]. Electrical power & energy systems, 2003, 25(2):97-105.

[36]ABIDO M A. A novel multiobjective evolutionary for multiobjective environmental/economic dispatch [J]. Electric power systems research, 2003(65):71-78.

[37]ABIDO M A. Environmental/Economic power dispatch using multiobjective evolutionary algorithms [J]. IEEE transactions on power systems, 2003, 18(4): 1529-1537.

[38]RUGHOOPUTH, HARRY C S, AH KING R T F. Environmental/economic dispatch of thermal units using an elitist multiobjective evolutionary algorithm[C]//IEEE international conference on industrial technology: IEEE, 2003, 1:48-53.

[39]ZHAO B, CAO Y J. Multiple objective particle swarm optimization technique for economic load dispatch [J]. Journal of Zhejiang university science A: science in engineering, 2005, 6(5):420-427.

[40]AH KING R T F, RUGHOOPUTH, HARRY C S, et al. Evolutionary multi-objective environmental economic dispatch: Stochastic versus deterministic approaches[C]//The third international conference on EMO-2005. Mexico : Springer Berlin Heidelberg , 2005:677-691.

[41]ABIDO M A. Multiobjective evolutionary algorithms for electric power dispatch problem [J].IEEE transactions on evolutionary computation, 2006, 10(3):315-329.

[42]VENKATESH P, LEE K Y. Multi-objective evolutionary programming for economic emission dispatch problem[C]// Power and energy society general meeting-conversion and delivery of electrical energy in the 21st century, Pittsburgh, PA: IEEE, 2008:1-8.

[43]AGRAWAL S, PANIGRAHI K B, TIWARI M K. Multiobjective particle swarm algorithm with fuzzy clustering for electrical power dispatch [J]. IEEE transactions on evolutionary computation, 2008, 12(5):529-541.

[44]CAI J, MA X Q, LI Q, et al. A Multi-objective chaotic ant swarm optimization for environmental/economic dispatch [J]. International journal of electrical power & energy systems, 2010, 32(5):337-344.

[45]WU L H, WANG Y N, YUAN X F, et al. Environmental/economic power dispatch problem using multi-objective differential evolution algorithm [J]. Electric power systems research, 2010, 80(9):1171-1181.

[46]BASU M. Economic environmental dispatch using multi-objective differential evolution [J]. Applied soft computing, 2011, 11(2):2845-2853.

[47]SIVASUBRAMANI S, SWARUP K S. Environmental/economic dispatch using multi-objective harmony search algorithm [J]. Electric power systems research, 2011, 81(9):1778-1785.

[48]PANIGRAHI B K, PANDI V R, SHARMAR, et al. Multiobjective bacteria foraging algorithm for electrical load dispatch problem [J]. Energy conversion & management, 2011, 52(2):1334-1342.

[49]ZHANG Y, GONG DW, DING ZH. A bare-bones multi-objective particle swarm optimization algorithm for environmental/economic dispatch [J]. Information sciences, 2012, 192(6):213-227.

[50]NIKNAM T, AZIZIPANAH A R, ROOSTA A, et al. A new multi-objective reserve constrained combined heat and power dynamic economic emission dispatch [J]. Energy, 2012, 42(1):530-545.

[51]GHASEMI A. A fuzzified Multi objective interactive honey bee mating optimization for environmental/economic power dispatch with valve point effect [J]. Electrical power & energy systems, 2013, 49:308-321.

[52]NIKNAM T, MOJARRAD H D, FIROUZI B B. A new optimization algorithm for multi-objective economic/emission dispatch [J]. International journal of electrical power & energy systems, 2013, 46(3):283-293.

[53]WU DQ, LIU L, GONG X J, et al. An efficient co-evolutionary particle swarm optimizer for solving multi-objective optimization problems[C]//27th Chinese control and decision conference (CCDC) ,Qingdao :IEEE, 2015:1975-1979.

[54]袁铁江,晁勤,李义岩,等.大规模风电并网电力系统经济调度中风电场出力的短期预测模型[J].中国电机工程学报,2010,30(13):23-27.

[55]WANG L F, SINGH C. Tradeoff between risk and cost in economic dispatch including wind power penetration using particle swarm optimization[C]//International conference on power system technology, Chongqing: IEEE, 2006:1-7.

[56]BRINI S, ABDALLAH H H, OUALI A. Economic dispatch for power system included wind and solar thermal energy [J]. Leonardo journal of sciences, 2009, 8(14):204-220.

[57]KUO C C. Wind energy dispatch considering environmental and economic factors [J]. Renewable energy, 2010, 35(10):2217-2227.

[58]MAN-IM A, ONGSAKUL W, SINGH J G, et al. Multi-objective economic dispatch considering wind generation uncertainty using non-dominated sorting particle swarm optimization[C]// 2014 International conference and utility exhibition on green energy for sustainable development (ICUE), Pattaya: IEEE, 2014:1-6.

[59]ZHU Y S, WANG J, QU B Y. Multi-objective economic emission dispatch considering wind power using evolutionary algorithm based on decomposition [J]. International journal of electrical power & energy systems, 2014, 63(12):434-445.

[60]DECKMYN C, VANDOORM T L, MORADZADEH M, et al. Multi-objective optimization for environomic scheduling in microgrids[C]// 2014 IEEE PES general meeting | conference & exposition, National Harbor, MD : IEEE, 2014:1-5.

[61]ADHVARYYU P K, CHATTOPADHYAY P K, BHATTACHARJYA A. Economic emission dispatch of wind power integrated combined heat and power system[C]//2014 Eighteenth National Power Systems Conference (NPSC), Guwahati: IEEE, 2014:1-6.

[62]BASU M. Particle swarm optimization based goal-attainment method for dynamic economic emission dispatch [J]. Electric power components & systems, 2006, 34(9):1015-1025.

[63]BASU M. Dynamic economic emission dispatch using evolutionary programming and fuzzy satisfying method [J]. International journal of emerging electric power systems, 2007, 8(4): 1-15.

[64]DEB K, BHASKARA U R N,KARTHIK S. Dynamic multi-objective optimization and decision-making using modified NSGA-II: A case study on hydro-thermal power scheduling[C]// 4th international conference, EMO 2007, Matsushima :Springer Berlin Heidelberg, 2007:803-817.

[65]BASU M. Dynamic economic emission dispatch using nondominated sorting genetic algorithm-II [J]. International journal of electrical power & energy systems, 2008, 78(2):140-149.

[66]LEE J C, LIN W M, LIAO G C, et al. Quantum genetic algorithm for dynamic economic dispatch with valve-point effects and including wind power system [J]. Energy power & energy system, 2011 (33):189-197.

[67]ABARGHOOEE R A, AGHAEI J. Stochastic dynamic economic emission dispatch considering wind power[C]// Power engineering and automation conference (PEAM),Wuhan : IEEE, 2011:158-161.

[68]BAHMANI F B, FARJAH E, AZIZIPANAH A R. An efficient scenario-based and fuzzy self-adaptive learning particle swarm optimization approach for dynamic economic emission dispatch considering load and wind power uncertainties [J]. Energy, 2013, 50(2):232-244.

Multi-objective Evolutionary Algorithm and Its Application in Electric Power Environment Economic Dispatch

XIAO Junming , ZHOU Qian , QU Boyang, WEI Xuehui

(School of Electric and Information Engineering, Zhongyuan University of Technology, Zhengzhou 450007, China)

Abstract:The power supply is vital for modern society while environmental economic dispatch of power system provides an effective solution to this problem. Multi-objective evolutionary algorithms have their unique advantages in solving power system environment economic dispatch problem. In this paper, the multi-objective evolutionary algorithms are briefly introduced in chronological order and then the applications of multi-objective evolutionary algorithms in environment economic dispatch are presented. In addition, some future research directions of this field are also discussed.

Key words:multi-objective optimization; multi-objective evolutionary algorithm; power system dispatch; economic environment dispatch

中图分类号：TM732

文献标志码：A

doi:10.3969/j.issn.1671-6833.201510023

作者简介：肖俊明(1960—)，男，河南郑州人，中原工学院教授，主要从事电气控制等研究，E-mail:xiaojunming528@163.com.通讯作者：瞿博阳(1984—)，男，河南焦作人，中原工学院副教授，主要从事智能优化算法等方面的研究.

基金项目：国家自然科学基金资助项目(61473266)；中国博士后科学基金资助项目(2014M552013)

收稿日期:2015-10-12；

修订日期：2015-12-28

文章编号:1671-6833(2016)02-0001-09

引用本文：肖俊明，周谦，瞿博阳，等.多目标进化算法及其在电力环境经济调度中的应用综述[J].郑州大学学报(工学版)，2016,37(2):1-9.