极限学习机优化及其拟合性分析

王　杰，苌群康，彭金柱

(郑州大学 电气工程学院，河南 郑州 450001)



极限学习机优化及其拟合性分析

王杰，苌群康，彭金柱

(郑州大学 电气工程学院，河南 郑州 450001)

摘要：运用烟花算法(fireworks algorithm, FWA)优化极限学习机(extreme learning machine, ELM).首先烟花算法经过多次的迭代，确定M个最优的烟花，并且以极限学习机测试样本的RMSE作为烟花算法每次迭代的适应度函数,达到优化极限学习机的输入权值矩阵和隐含层偏差的效果.最后根据广义逆求出输出矩阵.通过对一维sinC函数的测试结果表明,烟花算法优化极限学习机能够以较少的隐含层节点数目达到更高的精度，比极限学习机的测试误差降低了29.58%.在以上基础上又做了对高斯正态分布函数的拟合实验，验证了烟花算法优化极限学习机比极限学习机拥有更好的拟合性能.

关键词：烟花算法；ELM；测试误差；隐含层节点；FWAELM；拟合性

0引言

传统的神经网络因其强大的非线性拟合能力、很强的鲁棒性和记忆能力被广泛地应用于很多领域.极限学习机是一种先进的神经网络.输入权值和隐含层偏差根据输入神经元和隐含层节点数随机生成，输出权值矩阵根据隐含层输出矩阵的Moore-Penrose广义逆计算得到[1].尽管极限学习机相比于传统的神经网络有很多优点，但是并不能满足人们对更高精度和更快速度的追求，因此相继出现了很多优化极限学习机算法.例如粒子群优化极限学习机和小波核极限学习机等,分别优化了极限学习机的隐含层节点数和极限学习机的分类性能.

烟花算法研究的开创性论文是由谭营发表于首届国际群体智能大会(ICSI2010).该论文首次提出了受烟花爆炸启发的群体协同优化算法，即烟花算法.烟花算法希望寻求一种求解复杂问题全局最优解的高效方法.它具有求解复杂问题全局最优解的能力，故烟花算法可以运用到许多实际应用领域[2-3].

为了获得更高的精度和更好的拟合效果，笔者提出了用烟花算法优化极限学习机的方法.并通过实验证明，烟花极限学习机(fireworks algorithm extreme learning machine, FWAELM)能够达到更高的精度，并且所用的隐含层节点数目更少，对函数的拟合效果更好.

1极限学习机(ELM)

对于N个不相同的样本(xi,yi),其中，yi=[yi1,yi2,…,yin]T∈Rnyi=[yi1,yi2,…,yin]T∈Rn具有L个隐含层节点，激励函数G(x)的前馈神经网络的输出可以表示为[4]：

xi∈Rn,βi∈Rn，

(1)

式中：αi=[αi1,αi2,…,αin]T∈Rn为输入权值，θi=[θi1,θi2,…,θin]T∈Rn为输出权值；βi是第i个隐含层单元的偏置；αi·xi是向量αi和向量xi的内积；G为隐含层激励函数.

若具有L个隐含层节点的前馈神经网络以零误差逼近N个样本，有∑‖ti-yi‖=0,则存在αi、θi、βi使得

i=1,2，…，L.

(2)

由矩阵表示为：

Hθ=Y.

(3)

式中：H为网络隐含层的输出矩阵.

若前馈神经网络的输入权值和隐含层偏置是随机产生的，则根据Moore-Penrose广义逆计算可求得唯一的解

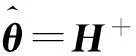
(4)

求输出权值矩阵就变成了求最小二乘解的问题，只需要求出输入权值的最小二乘解就能完成神经网络的训练.

2烟花算法(FWA)

烟花算法是一种群体智能算法，和粒子群算法相似，通过多次迭代寻求最优解，其过程描述参照文献[2].

烟花算法主要有爆炸算子、变异操作、映射规则和选择策略四大部分组成，其中爆炸算子包括爆炸强度、爆炸幅度、位移变异等操作；变异主要包括高斯变异操作[5-8]；选择策略包括有基于距离的选择和随机选择等操作.初始化的每个火花个数由式(5)计算出.在烟花算法中，产生火花个数的公式如下

(5)

式中：wi表示第i个烟花产生的火花个数，参数i的取值范围为1～N；m是常数，用来限制产生的火花总数；ymax是当前种群中适应度值最差个体的适应度值；f(xi) 表示个体xi的适应度值；参数ε是一个极小的常数，以避免出现分母为零的情况[5-7].

为了限制烟花爆炸产生火花的数目太多或太少，我为每一个烟花设定了如下的产生火花数量的限制公式

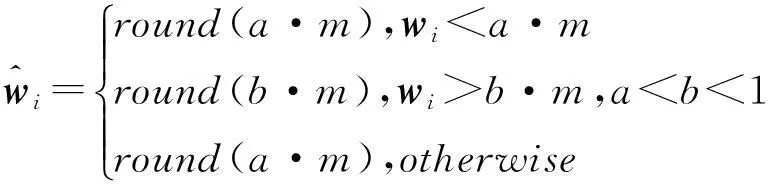
(6)

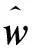
3烟花极限学习机(FWAELM)

ELM的输入权值和隐含层偏差是根据隐含层节点和神经元个数随机产生的，然后计算出输出权值矩阵.随机产生的输入权值和隐含层偏差只有少部分是比较优越的，其它偏差可能会造成误差偏大，甚至部分输入权值和隐含层偏差值为0，直接导致隐含层节点无效.

为解决ELM存在的以上问题，笔者提出了烟花极限学习机算法.FWA是一种新型的进化算法，在结果精度和收敛性能上具有很强的优势.FWA通过爆炸烟花的方式多次迭代选择出最优越的输入权值和隐含层偏差矩阵，把最适应输入权值和隐含层偏差组成新的矩阵，然后计算出输出权值矩阵.

3.1优化操作

在实现的过程中对算法进行了诸多的限制操作和变异操作.烟花爆炸范围的计算公式如下

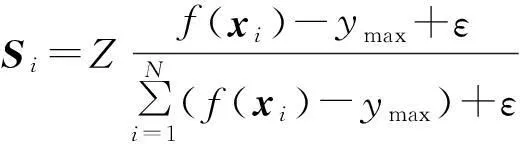
(7)

式中：Si表示第i个烟花的爆炸范围，即爆炸的火花将在这个范围内随机产生位移，但不能超过这个范围；Z是常数，表示最大的爆炸幅度；参数ymax是当前种群中适应度值最好个体的适应度值；f(xi)和参数ε的意义与公式(5)相同.

位移操作是对烟花的每一维进行位移，其公式如下

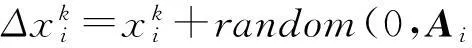
(8)

式中：random(0,Ai)表示在幅度Ai内生成的均匀随机数.

高斯变异增加了算法的突变性和多样性，表示第i个个体在第k维上的位置，此时高斯变异的计算方式如下

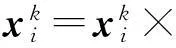
(9)

式中：g是服从均值为1，方差为1的高斯分布的随机数，g=N(1,1).

3.2算法步骤

算法维度大小为k=p(d+1)，d为输入神经元的个数，p为隐含层节点数.利用极限学习机计算出输出权值(激励函数选为‘sigmoid’)，将训练样本计算出的均方根误差(RMSE)作为烟花算法的适应度值函数.烟花算法的参数设置为m=64,a=0.04,b=0.8,Z=40.FWAELM的算法实现步骤如下所示.

①初始化N个烟花，确定烟花位置Hi，并根据适应函数计算出最优适应值B.

②设置初次迭代次数i=1.

③根据公式(5)和(6)计算每一个烟花产生子代火花的个数wi(i=1,2,…,N).

④根据公式(7)计算出每一个烟花的爆炸范围Gi.

⑤根据公式(8)对子代火花进行位移变异，对从k维中随机选择一定维度进行维度变异，在变异后的火花通过适应度值函数选择最优的火花Qi.

⑥随机选择m个烟花根据公式(9)进行高斯变异，并根据评价函数选出最优的火花Mi，把超出爆炸范围的火花通过公式(10)映射到范围之内.

⑦从Hi、Qi、Mi中选择最优的N个火花位置作为下一代火花爆炸位置.

⑧i=i+1;判断i=K(K为最大迭代次数)是否成立，不成立跳转到式(3)继续循环.

根据上述算法得到最优的火花位置，也就是最优的输入权值矩阵和隐含层偏差，然后根据极限学习机的广义逆求出输出权值矩阵.

4仿真实验

在论文中采用一维的sinC函数拟合实验来检验FWAELM的效果，sinC函数的表达式为.

(10)

各选取5 000个训练样本集合{xi,yi}和测试样本集合{xi,yi},训练样本和测试样本的xi都服从(-10,10)区间的均匀随机分布.为了能够使得线性回归拟合问题更真实，在训练样本中加入[-0.2,0.2]的白噪音，则训练样本集合为{xi,yi+ξi}.而测试样本集合为{xi,yi}.

4.1隐含层节点数目的影响

原理上，当迭代次数逐渐增加时测试误差减小幅度非常小，训练时间会增大.所以迭代次数不宜过大，适中即可.设置FWAELM的迭代次数为25，取20次试验结果的平均值(下同).测试隐含层节点数目对ELM和FWAELM的影响，其结果如图1所示.

从图1可知,当迭代次数都相同时，FWAELM比ELM测试误差先达到最小值，且FWAELM在隐含层节点数为10的时候RMSE达到最小值，而ELM在隐含层节点数目为17的时候RMSE达到最小值.由此说明FWAELM在测试误差最小时所用到的隐含层节点数目比ELM少用了7个.并且FWAELM比ELM最大的优点是前者所能达到的最小RMSE比ELM所能达到的RMSE降低了29.58%.当隐含层节点数逐渐增加到50的过程中，ELM的RMSE先减小后逐渐稳定.而FWAELM在隐含层节点数为10时达到最小，到50的过程中基本是稳定的.

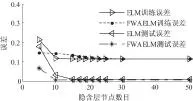
图1　隐含层节点数目对FWAELM和ELM影响

本实验还做了相同时间情况下的运行结果分析，分析表明，ELM在长的训练时间情况下反复运行，它的最优误差基本保持不变.

4.2迭代次数的影响

设定FWAELM的隐含层节点数为10，迭代次数i=1,3,…，29.测试迭代次数对FWAELM的影响，其结果如图2和图3所示.从图可知，随着迭代次数增加，FWAELM的测试误差和训练误差逐渐减小，当达到一定的迭代次数后，测试误差缓慢减小，直到趋于平稳.

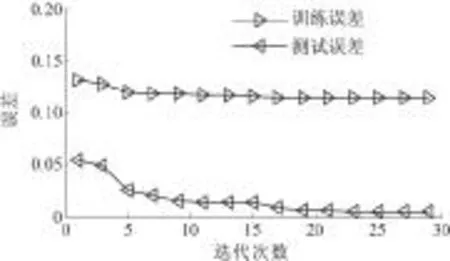
图2　迭代次数对FAELM误差的影响

另外，迭代次数增加也带来训练时间的增加.考虑到在测试误差减小不明显的情况下多次迭代增加训练时间，所以设置23为烟花极限学习机的最优迭代次数，即FWAELM的隐含层节点为10，迭代次数为23.

4.3函数拟合性分析

基于上述分析本实验做了FWAELM和ELM对sinC函数的拟合实验，ELM的结果如图3所示,FWAELM的结果如图4所示.

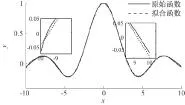
图3　ELM拟合sinC函数

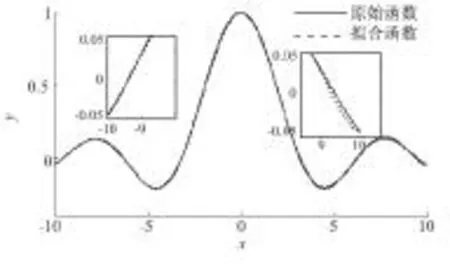
图4　FWAELM拟合sinC函数

从图3中可知，ELM在[-10，10]拟合过程中，分别在0附近及[-10,-6]和[8,10]中间出现了拟合误差较大的情况.图4中,FWAELM在整个拟合过程都比较平稳，出现的误差很小.由此可知，FWAELM的数据拟合效果明显优于ELM的，这也说明FWAELM的预测精度比ELM更高.

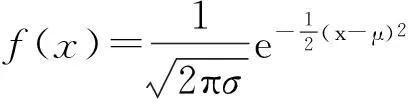
各选取5 000个训练样本集合{xj,yj}和测试样本{xj,yj},训练样本和测试样本都服从(-10,10)区间的均匀随机分布.为了使回归拟合问题更真实，在训练样本中加入[-0.2,0.2]的白噪音，则训练样本集合为{xj,yj+ξj}，而测试样本集为{xj,yj}.

设置FWAELM的隐含层节点数目为10，迭代次数为25，ELM的隐含层节点数目为50，结果如图5和图6所示.

从图5和图6的对比效果看，FWAELM的整个拟合过程相对平稳，而ELM在整个拟合过程中出现的误差相对较大;且FWAELM的拟合效果明显比ELM的拟合效果优越，因此，FWAELM比ELM具有更好的拟合效果.

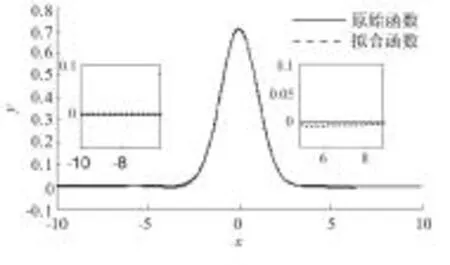
图5　FWAELM拟合高斯函数实验

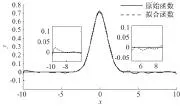
图6　ELM拟合高斯函数实验

4.4算法性能对比

在以上分析的基础上，笔者还做了FWAELM和ELM、支持向量机(SVM)及粒子群优化极限学习机(PSOELM)性能对比.设置FWAELM的隐含层节点数为10，设定迭代次数为23.设置ELM的隐含层节点为50个，100次重复运行后，求最优值.采用‘sigmoid’作为ELM的激励函数，迭代次数为25.PSOELM的隐含层节点设置为10，最大迭代次数设置为20. SVM采用libsvm工具包，其SVM的参数采用交叉验证来完成[8-10]，结果如表1所示.

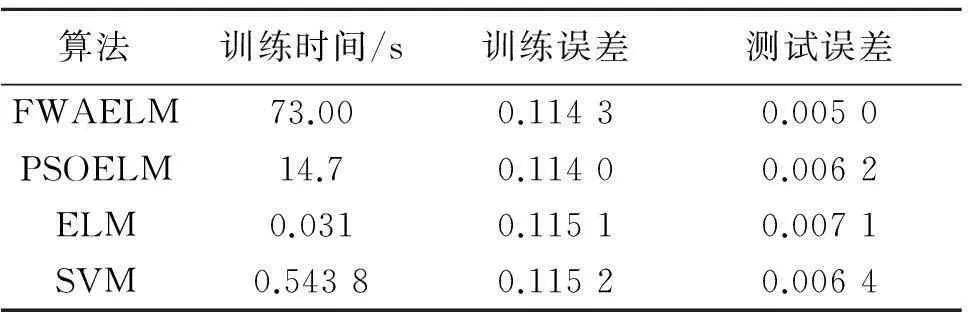
表1　算法性能对比

从表1中可知，FWAELM的测试误差是最小的，表明运用烟花算法能够降低ELM的测试误差，在4种算法的性能对比中,FWAELM最优.FWAELM只需要10个隐含层节点数目就能达到50个ELM隐含层数目的效果.

5结论

笔者提出运用烟花算法优化极限学习机的方法，采用烟花算法优化ELM的输入权值矩阵和隐含层偏差，结合了FWA和ELM的优点,给出了FWAELM的算法实现步骤.通过实验得出如下结论.

(1)当隐含层节点数目逐渐增加的时候，FWAELM比ELM以更少的隐含层节点达到最小测试误差,而且FWAELM的测试误差要比ELM的小.前者的训练时间相对后者要长，但是在追求更高精度的情况下，FWAELM比ELM有更高的优越性.

(2)随着迭代次数增加，FWAELM的训练误差和测试误差都会减小，当达到一定迭代次数的时候两者不再减小并趋于平稳，随着迭代次数的增加训练时间也会增加.

(3)运用两种算法分别对一维sin C函数和高斯正态分布函数进行拟合分析，表明FWAELM比ELM拥有更好的拟合性能.

(4)最后通过4种同类算法的最优误差进行性能对比，显示FWAELM的测试误差最小.

参考文献：

[1]HUANG G B, ZHU Q Y, Siew Cheekheong .Extreme learning machine: theory and applications [J]. Neurocomputing,2006,70(1):489-501.

[2]谭营，烟花算法引论[M]. 北京:科学出版社. 2015: 4.

[3]HE W R, MI G Y, TAN Y. Parameter optimization of local-concentration model for spam detection by using fireworks algorithm[C]. Lecture Notes in Computer Science,2013:439-450.

[4]DING K, ZHENG S Q, TAN Y. A GPU-based parallel fireworks algorithm for optimization[C]. Proceedings of the 2013 Genetic and Evolutionary Computation Conference,2013: 9-16.

[5]TAN Y, ZHU Y C. Fireworks algorithm for optimization [C].Lecture notes in computer science, 2010: 355-364.

[6]ZHENG S Q, ANDREAS J, TAN Y. Enhanced fireworks algorithm[C]. IEEE congress on evolutionary computation,2013: 2069-2077.

[7]阎新芳,张永坤,李腾,等. WSN中基于非均匀梯度的分簇拓扑算法[J].郑州大学学报(工学版),2014,35(6): 47-51.

[8]王杰,毕浩洋. 一种基于粒子群优化的极限学习机[J]. 郑州大学学报(理学版),2013,45(1): 100-104.

[9]陈其松.智能优化支持向量机预测算法及应用研究[D].贵阳：贵州大学信息学院, 2009.

[10]CHANG C C, LIN C J. LIBSVM: A library for support vector machines [J]. ACM Transactions on intelligent systems and technology, 2011, 2(3): 27.

The Optimization of the Extreme Learning Machine and Fitting Analysis

WANG Jie, CHANG Qunkang, PENG Jinzhu

(School of Electrical Engineering, Zhengzhou University, Zhengzhou 450001, China)

Abstract:The fireworks algorithm (FWA) is used to optimize the extreme learning machine (ELM) in this paper. Firstly, the FWA gain the M optimal fireworks through many iterations，and the RMSE of the extreme learning machine’s test samples is used as the fitness function in each iteration. Secondly, the optimization of the input weights and hidden layer deviation matrix of the extreme learning machine is achieved. Finally, the matrix output is obtained based on the generalized inverse. The test experiment of one-dimensional sinC function is conducted. The experimental results show that the fireworks algorithm extreme learning machine achieves higher accuracy with less number of hidden layer nodes, and the test error decreases 29.58% compared with the extreme learning machine. The fitting experiment of Gauss normal distribution function is conducted, and the experiment results further demonstrate that the FWAELM achieves a better fitting effect than the ELM.

Key words:fireworks algorithm; ELM; test error; node in hidden layer; FWAELM; fitting

中图分类号：TP183

文献标志码：A

doi:10.3969/j.issn.1671-6833.201505001

作者简介:王杰(1959—)，男，河南郑州人，郑州大学教授，博士，主要从事模式识别与智能控制研究，E-mail:wj@zzu.edu.cn.

基金项目:教育部高等学校博士学科点科研基金资助项目(20124101120001)；河南省教育厅科学技术研究重点资助项目(14A41300)；中国博士后科学基金面上资助项目(2014T70685;2013M541992)

收稿日期:2015-05-04；

修订日期：2015-08-20

文章编号:1671-6833(2016)02-0020-05

引用本文:王杰，苌群康，彭金柱.极限学习机优化及其拟合性分析[J].郑州大学学报(工学版)，2016,37(2):20-24.