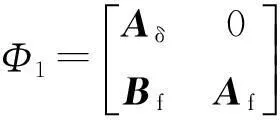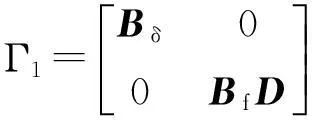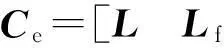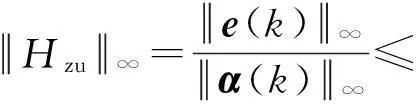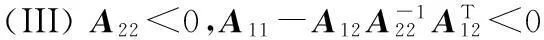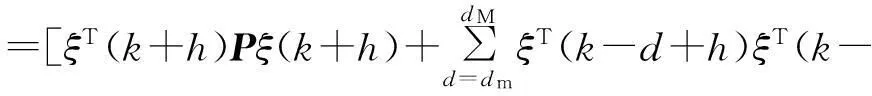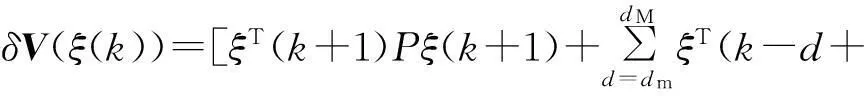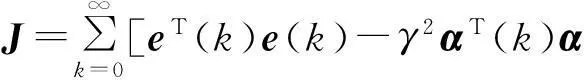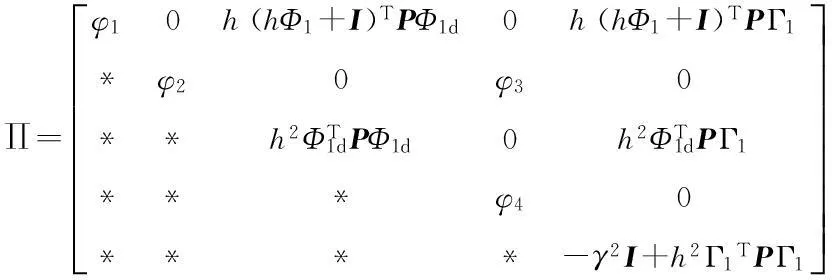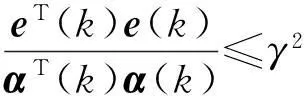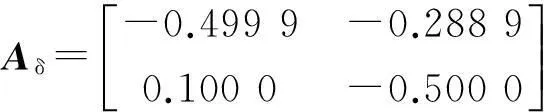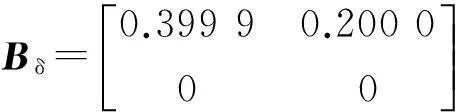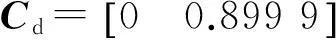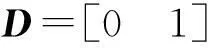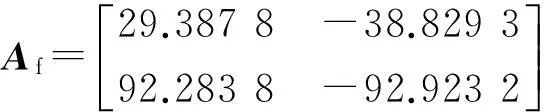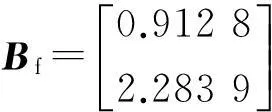基于Delta算子时变时延网络控制系统的H∞滤波

张端金，刘　雪，范　鑫

(郑州大学 信息工程学院，河南 郑州 450001)



基于Delta算子时变时延网络控制系统的H∞滤波

张端金，刘雪，范鑫

(郑州大学 信息工程学院，河南 郑州 450001)

摘要：研究了具有时变时延的网络控制系统滤波问题，设计了一个H(∞)滤波器使得时变时延系统保持稳定，基于Delta算子，使得连续域的设计方法可直接应用于离散域的设计.首先对时变时延的网络控制系统进行建模，构造了滤波误差系统，然后采用Lyapunov-Krasovskii泛函的方法，保留了经常被忽略的有用时延项，对网络控制系统的H(∞)滤波器误差系统进行性能分析，再通过一组线性矩阵不等式给出了使滤波误差系统渐近稳定的充分条件，并且得到了H(∞)滤波器的设计方法及导数表达式，最后通过数值例子表明本文方法的有效性.

关键词：网络控制系统；H(∞)滤波；Delta算子；时变时延

0引言

网络控制系统(NCS)是以互联网为传输媒介，旨在实现信息共享、传输以及控制，具有消耗成本低，使用灵活，维护较容易等特点[1]. 在信号处理和控制决策的具体实现方面，状态估计具有非常重要的作用，进而关于网络控制系统的滤波问题得到了广泛的关注.H∞滤波拥有很好的鲁棒性能，并且有很高的估计精度[2]. 关于网络控制系统的H∞滤波研究也越来越多，文献[3]深入研究了基于网络的离散时间Markov跳跃系统的H∞滤波.文献[4]探讨了同时带有混合时滞和数据包丢失的不确定非线性网络系统的H∞滤波问题. 但是，这些都只是分别在离散或者连续的情形下得出的结论，并未有一个方法将离散域和连续域的情况统一起来.

澳大利亚控制学家GOODWIN等提出了一种新的离散化连续系统的方法Delta算子[5]，在快速采样时能够使离散模型趋近于连续模型，Delta算子方法具有以下显著特点[6]：当采样周期趋近于零时，Delta算子系统所得结果与连续情形下的相应结果基本保持一致；其系统采样周期呈现为显示参数特征，这为分析不同采样周期控制系统的性能提供了极大的方便,在实现系统采样过程中，提供了良好的数字特征.

时延会降低系统性能，导致系统不稳定，是研究网络控制系统不可忽视的问题.文献[7]讨论了一类具有时延的网络系统的H∞滤波问题.文献[8]研究具有长时延及丢包的网络控制系统的H∞鲁棒滤波. 这些现有的研究成果均是在时延固定的情形下得到的，但是在实际应用中，时延是随时间变化的，因此研究时变时延的NCS具有重要意义.

笔者研究基于Delta算子的网络环境下存在时变时延系统的H∞滤波. 通过采用Lyapunov-Krasovskii泛函的方法，对网络控制系统的H∞滤波器误差系统进行性能分析，并以线性矩阵不等式的形式呈现了时变时延网络控制系统稳定的条件，进而通过数值例子证明了所设计滤波器的有效性且能满足H∞性能指标.

1问题描述

Delta算子[5]的定义式如下：

式中：h是采样周期，当h=0时，系统是连续系统；h≠0时，系统是离散系统. Delta算子可以将离散系统和连续系统统一起来.

假设一个Delta算子描述的时变时延离散系统表示如下：

(1)

式中：x(k)∈Rn为被控对象状态变量；y(k)∈Rr为对象输出向量；z(k)∈Rq为需要估计的信号向量；u(k)∈Rp为干扰输入向量；Aδ、Adδ、Bδ、C、Cd、D、L均是具有适当维数的已知实常数矩阵；d(k)是状态时滞，且d(k)满足

0

(2)

滤波器状态方程为:

(3)

定义如下状态向量

由Delta算子系统方程(1)和滤波器状态方程(3)得到系统状态方程为

δξ(k)=Φ1ξ(k)+Φ1dξ(k-d(k))+Γ1α(k).

(4)

其中：

可以得到，滤波误差系统状态方程为

(5)

设计时变时延NCS的H∞滤波器，需要同时满足下面条件:(1)能够满足滤波误差系统(5)渐近稳定;(2)能够满足H∞性能指标，即扰动输入到误差状态输出的H∞范数小于一个正数γ，即

2H∞滤波稳定性分析

为了分析滤波器的H∞性能，首先给出系统渐近稳定的定义.

定义1[8]：如果下列条件成立，一个Delta算子系统是渐近稳定的：

(i) V(x(k))≥0；当且仅当x(k)=0时，有V(x(k))=0.

(ii)δV(x(k))=[V(x(k+1))-V(x(k))]/h<0.

其中V(x(k))是关于x(k)的Lyapunov函数.

为了方便处理下面的定理证明，做出如下引理.

引理1[9](Schur complement lemma)对于给定的具有适当维数的实对称矩阵A11，A22，A12，则以下3个条件等价：

通过定义1中给出的系统稳定的条件，结合使用Lyapunov-Krasovskii函数的方法，给出如下定理.

定理1由式(5)描述的具有时变时延网络控制系统的滤波误差系统，使得系统满足渐近稳定性和范数有界条件的充分条件是：存在对称正定矩阵P和R满足

(6)

式中：

证明α(k)=0时，满足系统(5)渐近稳定.

构造下面的Lyapunov泛函

(k-d(k)).

式中：P、R为待定对称正定矩阵. 有

δV(ξ(k))=[V(ξ(k+h))-V(ξ(k))]/h<0

当h=1时，

其中：Ω=

δV(ξ(k))<0等价于

只需要Ω<0，上述不等式即可成立，由不等式(6)，利用Schur补引理可以得到Ω<0，由此可得到使滤波误差系统(5)满足是渐近稳定的条件.

(7)

其中：

ζ(k)=[ξT(k+1)ξT(k)ξT(k-dm)ξT(k-

dM+1)α(k)]；

由(6)知：J<0，也即:

eT(k)e(k)-γ2αT(k)α(k)<0.

有：

定理得证.

3H∞滤波器设计

定理2对于由式(1)描述的具有时变时延的Delta离散系统，γ>0，若系统初值为0，可以由下面的线性矩阵不等式得到对称正定矩阵F1、P1、R1、R3、P3、F3和矩阵F2、P2、R2，则系统是渐近稳定的.

(8)

其中：

证明:令

由Schur补性质可以得到：

(9)

定理得证.

4算例分析

考虑系统(1)，其参数矩阵为

利用MATLAB中的LMI工具箱，求解不等式(8)，可以得到如下结果.当dm=0.45时，得到时滞最大值dM=1.89，H∞扰动抑制度为γ=0.415 2，滤波器的系数矩阵为：

当取dm=0.5，dM=0.68时，H∞扰动抑制度为γ=0.202 9，与文献[7]相比，H∞扰动抑制度要低一些，可得滤波器的系数矩阵为：

图1为待测信号z(k)真实值和估计值的比较，

图1　真实值和估计值的比较

由结果可以看出，如果时滞时延范围比较小，H∞扰动抑制度比较小，则得到的滤波器性能也比较稳定.

5结论

笔者研究了具有时变时延的网络控制系统的滤波问题，通过Lyapunov泛函和H∞滤波方法，且在离散化系统的时候运用了Delta算子的方法，求解Lyapunov泛函时不仅降低了设计的保守性，所得结果也表明研究方法是可行的，且时延范围和滤波器性能稳定性呈反向变化.

参考文献：

[1]游科友,谢立华.网络控制系统的最新研究综述[J].自动化学报, 2013, 39(2):101-117.

[2]MAO Z H, JIANG B. H-infinity fault detection filter design for networked control systems modeled by discrete Markovian jump systems[J]. IET control theory and applications, 2007, 1(5):1336-1343.

[3]介晓婧,张端金,汪爱娟.基于网络的离散时间Markov跳跃系统滤波[J].中南大学学报(自然科学版)，2013, 44(S1):119-122.

[4]赵立英, 窦利亚. 具有随机时滞和丢包的非线性网络控制系统的滤波器设计[J]. 中南大学学报(自然科学版), 2014, 45(12): 4224-4231.

[5]MIDDLETON R H, GOODWIN G C. Improved finite word length characteristics in digital control using delta operator[J].IEEE trans.on automatic control, 1986, 31(11):1015-1021.

[6]ZHANG D J, ZHOU H C. Fault detection of delta operator formulated networked control systems[C]//Proceedings of the 25th chinese control and decision conference, Guiyang, 2013:1039-1043.

[7]ZHANG X M, HAN Q L. Robust H∞filtering for a class of uncertain linear systems with time-varying delay[J]. Automatica, 2008, 44(1):157-166.

[8]蔡云泽, 潘宁, 许晓鸣. 具有长时延及丢包的网络控制系统鲁棒滤波[J].控制与决策, 2010, 12(1):1826-1836.

[9]BOYD S, GHAOUI L E, FERON E. et al. Linear matrix inequalities in systems and control theory [M]. Philadelphia: SIAM,1994:11-16.

[10]HE Y, WANG Q G, LIN C. et al. Delay-range-dependent stability for systems with time-varying delay[J]. Automatica, 2007, 43(2):371-376.

H-infinity Filtering for Networked Control Systems with Time-varying Delay Using Delta Operator Approach

ZHANG Duanjin, LIU Xue, FAN Xin

(School of Information Engineering, Zhengzhou University, Zhengzhou 450001, China)

Abstract:This paper is concerned with the problem of filtering for network-based systems with time-varying delay. A filter is designed to ensure the stability of the system. The filtering problems can be studied in the combination form via Delta operator approach. Firstly, a model is constructed, then by using a Lyapunov-Krasovskii function the performance analysis of network-based H-infinity filtering-error systems were proposed by retaining some useful time-delay terms. And a sufficient condition of asymptotically stability for filtering error system and the design method of H-infinity filter are derived in terms of several linear matrix inequalities. A numerical example shows the effectiveness of the proposed approach.

Key words:networked control system; H(∞) filtering; Delta operator; time-varying delay

中图分类号：TP273

文献标志码：A

doi:10.3969/j.issn.1671-6833.201405039

作者简介:张端金(1966—)，男，湖北荆州人，郑州大学教授，博导，主要从事网络系统故障检测与滤波研究，E-mail: djzhang@zzu.edu.cn.

基金项目：国家自然科学基金资助项目(61471323)；河南省教育厅科学技术研究重点资助项目(14A120004)

收稿日期:2014-05-20；

修订日期：2015-02-28

文章编号:1671-6833(2016)02-0010-05

引用本文：张瑞金，刘雪，范鑫.基于Delta算子时变时延网络控制系统的H∞滤波[J].郑州大学学报(工学版)，2016,37(2):10-14.