不确定T-S模糊系统的跟踪控制器设计

张恒艳，高中文，李文龙，宋伟伟，黄　玲

(哈尔滨理工大学 自动化学院，黑龙江 哈尔滨 150080)



不确定T-S模糊系统的跟踪控制器设计

张恒艳，高中文，李文龙，宋伟伟，黄玲

(哈尔滨理工大学 自动化学院，黑龙江 哈尔滨 150080)

摘要：研究基于观测器的不确定T-S模糊系统的跟踪控制器设计问题.利用T-S模糊方法对含有不确定性的非线性被控对象进行建模，对于给定代表系统期望状态的参考模型，在系统状态不可测及不确定项满足有界条件下，利用并行分布补偿的方法(parallel distributed compensation)设计基于观测器的模糊控制器，保证对于参考模型状态的跟踪，同时抑制扰动对跟踪误差的影响.借助Lyapunov稳定性定理及舒尔补引理将跟踪控制器的设计问题转化为一组线性矩阵不等式(linear matrix inequality)的可行解问题.该方法简单实用，仿真实例验证了此种方法的有效性与正确性.

关键词：T-S模糊系统；不确定性；观测器；H(∞)跟踪性能；线性矩阵不等式(LMI)

0前言

在控制理论领域的研究中，利用T-S模糊模型可以实现对非线性系统的逼近，基于T-S模糊控制策略去处理模糊控制系统中存在的非线性具有很大的优势.近年来，随着T-S模糊理论的不断完善，非线性系统的鲁棒镇定问题成为控制领域研究的重点.文献[1-3]分别针对带有参数不确定，时滞和非线性项的T-S模糊系统的鲁棒镇定问题展开研究，给出了鲁棒镇定的条件以及控制器的设计方法.文献[4]将模糊系统的鲁棒镇定条件表述为一系列矩阵不等式的可行性问题，实现了控制器的求解.在实际应用中，为了使系统的状态或输出尽可能地接近给定信号，实现跟踪控制，必须要设计跟踪控制器来满足系统的控制要求.文献[5]在考虑T-S模糊模型建模误差的前提下，对稳定的线性参考模型实现跟踪控制，得到了保证跟踪误差系统稳定的约束条件.在此基础上，文献[6]提出了一种新的H∞性能指标，研究了受控输出变量中控制系数不为零情况下的跟踪控制问题，通过对模糊控制器的设计，实现了状态变量与参考变量的高精度吻合.文献[7]针对系统状态不可测的情况，设计了基于观测器的跟踪控制器，实现对系统状态的跟踪.文献[8]研究系统存在有界外部扰动条件下基于状态反馈的H∞渐近跟踪控制器设计问题.

综上，针对T-S模糊不确定系统，在状态未知条件下的H∞渐近跟踪控制还没有研究，笔者将探讨这方面的问题.首先，基于T-S模糊模型对含有不确定性的非线性系统进行建模，然后给定系统的跟踪参考模型，在不确定项满足有界的条件下，设计以模糊观测器为基础的模糊控制器.通过选取适当的李雅普诺夫函数，推导出H∞跟踪控制器存在的充分条件，该条件具有线性矩阵不等式形式，最后，通过对相应的线性矩阵不等式(linear matrix inequality,LMI)求解，构造模糊控制器与模糊观测器。

1问题描述

由T-S模糊模型描述的不确定非线性系统，定义规则如下.

(Bi+ΔBi)u(t)+di(x,t)，

(1)

y(t)=Cix(t)+v(t)，i=1,2,…,r.

(2)

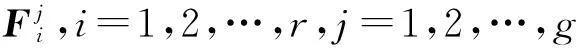
(3)

利用单点模糊化、乘积推理、中心加权反模糊化的方法可以得到模糊系统模型

(Bi+ΔBi)u(t)+di(x,t)].

(4)

(5)

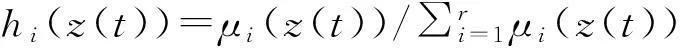
对于系统中的扰动，引进下面的假设.

假设1模型(4)中的扰动di(x,t)满足

(6)

为了推导出笔者的结论，需要借助以下对于有界不确定性的处理方法.

引理1[9]给定适当维数的矩阵Y、D和E，其中Y是对称的，则有

Y+DFE+ETFTDT<0.

对于所有满足FTF≤I的矩阵成立，当且仅当存在一个常数ε>0，使得

Y+εDDT+ε-1ETE<0.

(7)

成立.

定义参考模型：

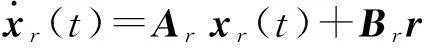
(8)

式中：Ar∈Rn×n为系统的渐近稳定矩阵；Br∈Rm×1为输入矩阵；xr(t)为参考状态；r(t)为有界参考输入.

观测器采用和被控对象相同的模糊规则，第i个规则为:

(9)

(10)

全局观测器表示为

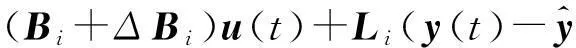
(11)

(12)

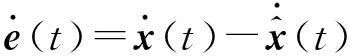
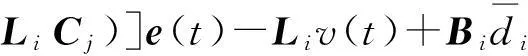
(13)

采用和被控对象相同的控制规则，则全局模糊控制器为

(14)

从而得到如下的闭环增广系统：

(15)

式中：

对于增广系统(15)，考虑如下H∞扰动抑制性能指标

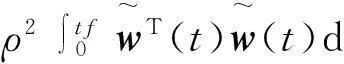
(16)

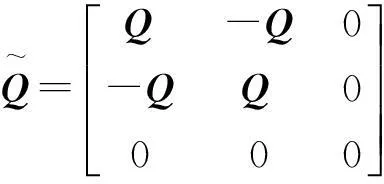
2基于观测器的模糊跟踪控制设计

(17)

成立，则系统(15)满足H∞跟踪性能(16) .

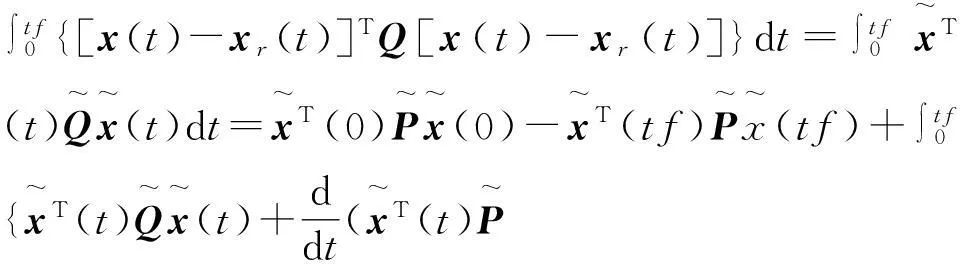
由定理1可得

证毕.

定理2在非线性系统(15)中，如果存在正定对称矩阵P11、P22、P33、Q、Kj及标量εi>0,使下面的线性矩阵不等式成立

(18)

则系统(15)满足H∞跟踪性能(16).

式中：

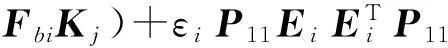
FbiKj)T(FbiKj)；

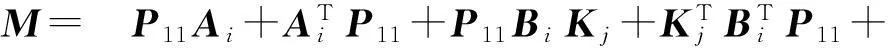
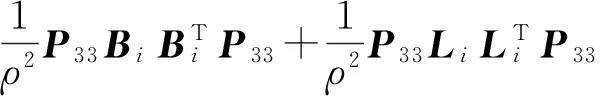
借助引理1，上式可转化为：

通过定义Sij,i=1,2,3,i≤j上式转化为式(18)，定理得证.定理给出了状态跟踪控制器存在的充分条件，可以证明在该条件下，闭环系统是二次稳定的.

(19)

那么闭环系统(15)二次稳定.

可以看出在式(17)满足的条件下，式(19)一定满足，因此条件(18)保证了T-S模糊系统(15)二次稳定，从而说明设计的基于观测器的控制器实现了对于参考模型状态的跟踪.即被控对象(4)实现了对参考模型(8)状态的跟踪.

定理2建立了保证系统(4)实现H∞渐近跟踪参考模型(8)的充分条件，下面给出求解不等式的方法.

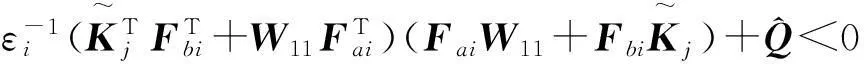
利用Schur补引理处理后有：

(20)

同理，S33<0，可以求解出P33与L.将所求解的值代入式(18)可以得到P22的值.

3仿真实例

含有不确定性的T-S模糊系统的参数给定如下：

系统的仿真曲线如图1所示，跟踪误差如图2所示.可以看出，相比于文献[1-3]，对于含有不确定性的T-S模糊系统，笔者设计的基于观测器的控制器，不仅可以使闭环系统鲁棒镇定，而且可以实现被控对象的状态在满足H∞性能指标ρ=0.1的条件下对系统状态的跟踪，响应时间在2 000～2 500 s之间，且具有很好的跟踪效果.

4结论

研究了一类以观测器为基础的不确定T-S

图1　响应曲线

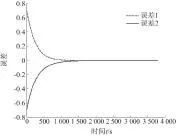
图2　跟踪误差曲线

模糊系统的跟踪控制问题.实现了在系统状态不可测及不确定性有界情况下对系统状态的跟踪，以及外界扰动的抑制，并将控制器的设计转化为线性不等式的求解，步骤简单方便，仿真实例验证了此种方法的有效性与正确性.

参考文献：

[1]齐丽,杨俊友.基于观测器的不确定T-S模糊系统的鲁棒镇定[J]．控制理论与应用, 2010, 27(5):

627-630.

[2]宋晓娜,刘磊坡.一类非线性T-S模糊时滞系统的鲁棒观测器型H∞控制器设计[J]．物 理 学 报,2013，62(21):1-11.

[3]王瑷珲,张强,王东云,等.基于滑模变结构的IPMC跟踪控制系统设计[J]．郑州大学学报(工学版), 2014，35(6):104-107.

[4]DUAN G R,YU H H．LMIs in Control Systems Analysis Design and Applications[M]．CRC Press, 2013.

[5]于洋,王巍.基于T-S模型的一类非线性系统的鲁棒跟踪控制[J]．辽宁工业大学学报(自然科学版),2013,33(4):220-226.

[6]常晓恒,井元伟,高曦莹,刘晓平.T-S模糊系统H∞跟踪控制设计[J]．控制与决策,2008,23(3)：329-332.

[7]TSENG C S, CHEN B S, UANG H J. Fuzzy tracking control design for nonlinear dynamic systems via T-S fuzzy model[J]．IEEE transactions on fuzzy systems．2001,9(3):381-392.

[8]王艳华,王志飞.一类不确定 T-S 模糊系统的H∞跟踪控制[J]．湖北文理学院学报,2014,35(8):11-15.

The Design of Tracking Controller for T-S Fuzzy Systems with Uncertainty

ZHANG Hengyan, GAO Zhongwen, LI Wenlong, SONG Weiwei, HUANG Ling

(School of Automation, Harbin University of Science and Technology, Harbin 150080, China)

Abstract:The tracking controller for T-S fuzzy systems with uncertainty is designed based on the observer. T-S fuzzy method is used to model the nonlinear controlled object with uncertainty. For given expected state tracking model, when the state of the system is unmeasurable and the uncertainties are bounded, a fuzzy controller based on the observer is designed by means of parallel distributed compensation (PDC). The controller guarantees that the states of the close-loop system track the states of the reference model, and that the influence of the disturbance is reduced. By Lyapunov stability theorem and Shur Complement Lemma, the design of the tracking controller is transformed into a feasible problem for a set of linear matrix inequalities (LMI). The simulation example is given to testify the validity and efficiency of the proposed method.

Key words:T-S fuzzy tracking system; uncertainty; H(∞) tracking performance; linear matrix inequalities (LMI)

中图分类号：TP273

文献标志码：A

doi:10.3969/j.issn.1671-6833.201504057

通讯作者:黄玲 (1975—)，女，河南人，哈尔滨理工大学教授，博士，主要从事网络控制系统分析与控制、信号处理(滤波)、时滞系统研究等，E-mail：mail_huangling@163.com.

基金项目:黑龙江省2014年度科技资助项目(12541118)

收稿日期:2015-04-24；

修订日期：2015-08-18

文章编号:1671-6833(2016)02-0015-05

引用本文:张恒艳，高中文，李文龙，等.不确定T-S模糊系统的跟踪控制器设计[J].郑州大学学报(工学版)，2016,37(2):15-19.