对称性在电磁场方向判断中的应用
梁 雄 赖国忠
对称性在电磁场方向判断中的应用
梁 雄赖国忠
摘 要:在求解电磁场问题中,往往都需要判明总电场或磁场的方向,才好根据电场或磁场分布特点选取相应定理或定律来求解,分析常用的方法都是利用对称位置上取电荷元和电流元,再利用电磁场的叠加原理判断其方向.本文利用带电体和载流导体的对称性直接判断电场方向,分析过程更加简洁,不必涉及太多物理知识,这种分析方法对于初学电磁学的学生来说更加容易接受.
关键词:对称性电场方向磁场方向叠加原理高斯定理
1引言
对称性分析在大学物理教学有着极其重要的地位[1],有相当多的文献从不同角度来探讨对称性在求解电场和磁场中的应用,有的文献利用真矢量和膺矢量分析电磁场方向问题[2,3],有的文献将所研究对象分割成若干微元(电荷元和电流元),再利用分布对称性以及叠加原理分析出整体电场或磁场方向[4].应用高斯定理抑或是应用叠加原理来求解电场,都需要分析电场方向,应用安培环路定理或毕奥-萨伐尔定律求解具有对称性载流导体的磁场时,分析磁场方向也是必不可少的一个过程.本文直接从带电体(载流导线)的对称着手,结合矢量绕轴旋转的变化规律分析出教材中几个典型电磁场例子[5,6]在对称轴上任意点的电场(磁场)方向.
2理论依据
将矢量A沿两个方向——垂直轴线和平行于轴线分解,分解得到的分量分别记为A⊥和A//,如图1(a)所示.如果将矢量A绕着转轴转过一个角度α,那么A//保持不变,而A⊥随转轴转过相同角度α,因此旋转后得到的矢量方向将变化,即与旋转前的矢量不等,图1(b)给出了矢量A绕轴转180°变成矢量A′这一情况,由此可推导出以下两个结论.
结论1:当且仅当矢量垂直分量为零时,旋转前后矢量保持不变.
结论2:当平行分量为零,如果旋转一个180°角时,旋转后的矢量方向与旋转前方向相反了.
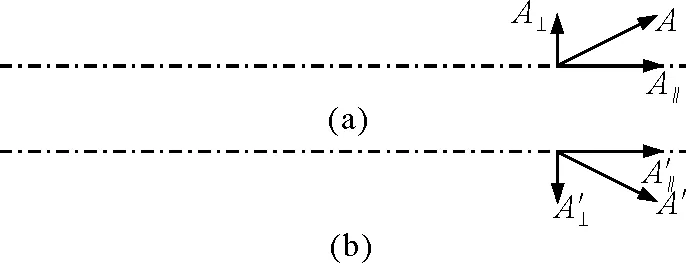
图1 矢量绕轴旋转
3对称载流导线的磁场方向
3.1对称带电体在其对称轴上任一点的电场方向
利用这一特性并结合带电体的对称性就较容易判断带电体在空间某一点的电场方向.图2给出大学物理教材中常提到的3种均匀带电体——带电球体(球面)、带电圆环和带电直导线,假定它们在对称轴的方向如图所示.现将它们绕着各自的对称轴旋转180°角,会发现电场方向发生了变化,但带电体在旋转前后其电荷分布并未发生改变,这就违背了电场的唯一性.因此要使得旋转后的电场方向不变,按结论1可知:在它们的对称轴上某点的电场方向只能沿着对称轴方向.
在此基础上可将上面3个例子的结论推广为:如果带电体存在一个轴,绕着这个轴旋转某一角度(例如180°)后,电荷分布未发生变化,则在该轴上任意点的电场方向必定沿着轴线方向.

图2 几种典型带电体的电场方向
3.2载流圆线圈在其轴线上某点的磁场方向
假设在载流圆线圈轴线上的磁感应强度方向如图3所示,现将圆线圈绕其轴线转过一个任意角度,发现电流分布未发生变化,该点处的磁场方向却发生了改变,这违反了磁场方向的唯一性.因此根据结论1可知:载流圆线圈轴线上的磁感应强度方向一定沿着轴线方向.

图3 载流圆线圈在其轴线上某点的磁场方向
3.3同轴电缆内部磁场方向
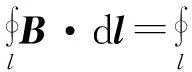

图4 同轴电缆内部磁场分析流程用的横截面示意图
4结论
本文直接借用了矢量绕着某轴心旋转的规律,结合带电体和载流导线的对称性,使得对电场方向和磁场方向的分析更加快捷,由于不需太多的物理知识,对于学生也容易理解,对于培养学生逻辑思维能力有一定的帮助.
参 考 文 献
1陈熙谋,赵凯华.电磁学教学中对称性分析的积极意义. 大学物理,2005,24(4): 3~5
2黄亦斌,聂义友.镜象对称性在电磁学中的应用. 大学物理,2007, 26(10): 24~26
3刘国钰.浅析对称性分析在电磁学中的应用.职业技术教育, 2013,34(2):48~50
4余仕成, 周金华. 载流长直螺线管和螺绕环的磁场对称性分析. 武汉工程大学学报, 2010, 32(5):106~107
5马文蔚, 周雨青, 解希顺. 物理学教程(下册)(第2版). 北京:高等教育出版社, 2006.1~93
6梁灿彬, 秦光戎, 梁竹健. 电磁学(第2版). 北京:高等教育出版社, 2004
7赵近芳,王登龙.大学物理学(下)(第4版).北京:北京邮电大学出版社,2014.1~88
(收稿日期:2015-11-06)
*作者简介:梁雄(1976-),男,讲师,主要从事大学物理及其实验教学研究.
(龙岩学院福建 龙岩364012)

