求解分裂可行问题的一种松弛投影算法

刘 川 何

(重庆师范大学 数学学院，重庆 401331)



求解分裂可行问题的一种松弛投影算法

刘 川 何

(重庆师范大学 数学学院，重庆 401331)

摘要：主要研究了分裂可行问题的一种修正CQ算法的松弛形式，在已有CQ算法的一种修正形式上提出了其松弛算法，并证明了其收敛性，当参数满足一定条件时，该算法的收敛性成立.

关键词：松弛投影算法；分裂可行问题；收敛

0引言

设C，Q分别是Rn和Rm中的非空闭凸子集，A是实矩阵且A∈Rm×n，分裂可行问题(SFP)[1]就是要找到这样的元素x(如果这样的元素x是存在的).

x∈C，Ax∈Q

(1)

为了解决SFP问题，很多学者提出了各种各样的算法，其中Byrne提出了CQ算法[2]来解决SFP，其迭代公式为

(2)

受Byrne提出的CQ算法的影响，Wang和Xu[3]提出了如下迭代方法：对于任意的初始迭代点x1∈H,其中H为Hilbert空间，定义它的迭代序列为

(3)

其中，{αn}⊂(0,1).当{αn}满足下列条件时：

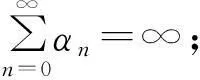
式(3)强收敛于式(1)的范数最小解.Wang[4]在式(3)的基础上提出了一种更一般的的形式，使得该算法的参数条件更弱.其算法如下：对于任意的初始迭代点x1∈H,其中H为Hilbert空间，定义它的迭代序列为

(4)

其中{αn}⊂(0,1).

1预备知识

定义1设x，y为n维欧式空间的任意向量，x和y的内积定义为

定义2设x为n维欧式空间的任意向量，Ω为n维欧式空间的任意非空闭凸子集，则x到Ω上的投影定义为

引理1设Ω为n维欧式空间的非空闭凸子集，则对于投影算子PΩ(x)有以下结论成立：

① ≥0,∀x∈Rn,y∈Ω;

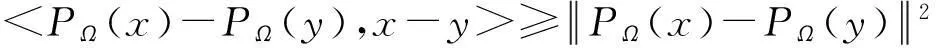
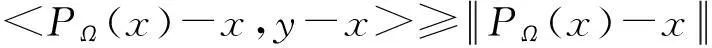
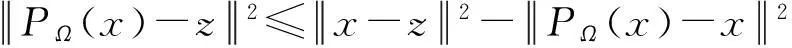
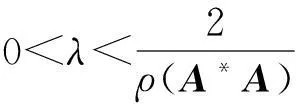
①U是均值算子,即U=(1-β)I+βV,其中β∈(0,1)是一个常数并且V:H→H是非扩张算子，其中H为Hilbert空间；

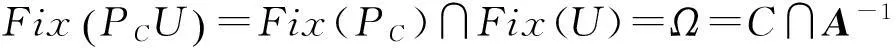
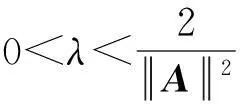
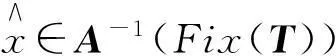
2主要结果

下面给出对式(4)的松弛形式.

算法1对于任意的初始迭代点x1∈H,其中H为Hilbert空间，定义它的迭代序列为

(5)

其中{αn}是一个序列，且{αn}⊂(0,1).

定理1假设下面条件成立：

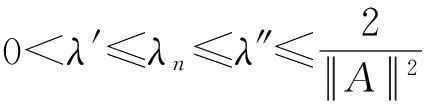
则式(5)强收敛于PΩ(0),其中Ω表示式(1)的解集.

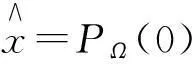
所以{xn}是有界的，并且{yn}也是有界的.

下面证明强收敛性，由引理5可得

(6)

运用引理2可知

(7)

由式(6)(7)可以推出下面不等式(8)

(9)

因为{xn}是有界的，所以存在子列{xnk}使得

(10)

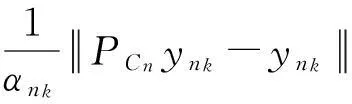
参考文献(References)：

[1]CENSOR Y,ELFVING T.A Multiprojection Algorithm Using Bregman Projections in a Product Space[J].Numerical Algorithms,1994,8(2/4):221-239

[2] BYRNE C.Iterative Oblique Projection onto Convex Sets and the Split Feasibility Problem[J].Inverse Problems,2002,18(2):441-453

[3] WANG F,XU H.K.Approximating Curve and Strong Convergence of the CQ Algorithm for the Split Feasibility Problem[J].Journal of Inequalities and Applications,2010(513):441-453

[4] 王亚敏.非线性优化问题中的一些迭代算法的强收敛性[D].上海：华东理工大学，2014

WANG Y M.Strong Convergence for Some Iterative Methods of Nonlinear Optimization Prblem[D].Shanghai:East China University of Science and Technology,2014

[5] MAINGE P E,MARUSTER S.Convergence in Norm of Modified Krasnoselski-Mann Iterations for Fixed Points of Demicontractive Mappings[J].Applied Mathematics and Computation,2011(217):9864-9874

[6] CUI H H,SU M L,WANG F H.Damped Projection Method for Split Common Fixed Problems[J].Journal of Inequalities and Applications ,2013(123):1009-1016

[7] 王宜举，修乃华.非线性规划理论与算法[M].西安：陕西科学技术出版社，2004

WANG Y J,XIU N H.Nonlinear Programming Theory and Algorithms[M].Xi’an:Shanxi Science and Technology Press,2004

责任编辑：李翠薇

A Relaxation Projection Algorithm for Solving the Split Feasibility Problem

LIU Chuan-he

(School of Mathematics, Chongqing Normal University, Chongqing 401331, China)

Abstract：This paper mainly studies a modified relaxation form of CQ algorithm of split feasibility problem, proposes its relaxation algorithm based on a modified form of existed CQ algorithm, proves its convergence and indicates that the convergence of this algorithm is established when the parameters satisfy certain conditions.

Key words：relaxation projection algorithm; split feasibility problem; convergence

中图分类号：O242

文献标志码：A

文章编号：1672-058X(2016)01-0016-03

作者简介：刘川何(1990-)，男，四川渠县人，硕士研究生，从事系统优化理论及其应用研究.

收稿日期：2015-09-02；修回日期：2015-09-23.

doi:10.16055/j.issn.1672-058X.2016.0001.003