推广的预矫正邻近点法求解可分凸优化问题*

罗　立

(重庆师范大学 数学学院，重庆 401331)



推广的预矫正邻近点法求解可分凸优化问题*

罗立

(重庆师范大学 数学学院，重庆 401331)

摘要：考虑目标函数能够分解成n个独立的凸函数,其约束条件为线性约束的可分凸优化问题.呈现了一种推广的预测矫正邻近乘子法来求解可分凸优化问题.算法在迭代中利用二次项代替了增广拉格朗日函数的增广项，算法既有邻近乘子法的特性，又有可以平行计算，并且在较弱的条件下，能保证全局收敛.

关键词：可分凸优化；增广拉格朗日；邻近法；分裂法

0引言

具体的可分凸优化问题如下：

(P)

(1)

其中fi:Rni→R是闭真凸函数,Ai是给定的l×ni矩阵.很多凸规划问题都可被整理成问题式(1)的形式,如[1,2].原问题的拉格朗日函数被定义为

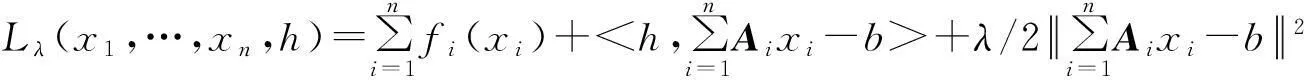
根据邻近点乘子法，得到：

(2)

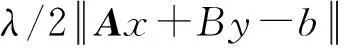
这里的pk实际上是乘子的一个近似值，在下面2中介绍了基于邻近点的分裂法，3中提出了具体的算法，4中证明了它的收敛性，5中进行数值算例.

1PCMP算法

若f(x)是闭真凸函数,那么算法

就是邻近点分裂算法.其中λk是正标量

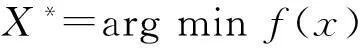
文献[5]中，提出了如下的算法：

S1.pk+1:=hk+λk(Axk-zk)

S3.hk+1:=hk+λk(Axk+1-zk+1)

算法在对偶变量上有两次迭代，在原始变量上有一次迭代；它是基于邻近点算法和对偶问题的应用；它是邻近点分裂法的另外一种表现形式.方法不仅保留了邻近点乘子法的很好的性质，而且还具有全局收敛性，同时没有了增广项给原问题带来的不可分的性质.算法实际上可以被看成是线性化+并行+不精确的一种方法.

2EPCMP算法

S0.k：=0.

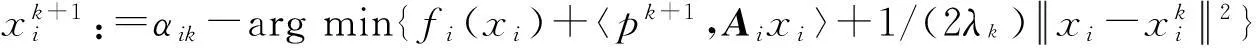
为了后续证明,在此先定义：

3收敛性

引理1∀k≥0，以下不等式成立

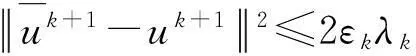
引理2∀k≥0，以下不等式成立

证明由引理1中的①得到

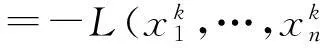
(3)

(4)

再将式(3)(4)相加并整理后引理2中的②得证.

以下引理是EPCMP算法的收敛性证明的关键.

证明将引理2中的两个不等式①和②相加得到：

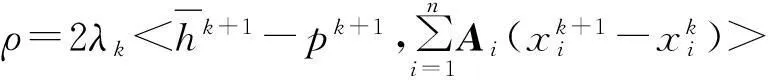
(5)

因为ε>0，再由三角不等式

(6)

(7)

其中0≤ci<∞.将式(11)代入式(10)得到

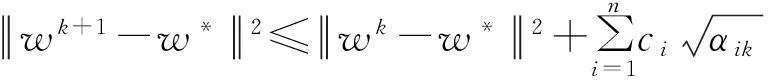
(8)

下证收敛性

由式(5)，两边同时取极限得到如下等式：

由于{wk}有界，则存在w∞，使得wkj→w∞.下证w∞为L(x1,…,xn,h)鞍点.

由引理1

(9)

同理，

(10)

下证鞍点唯一性

两边同时取极限

4举例

下面考虑这样一个问题

上述例子的最优点为(0,-1,0)，最优值为0.

迭代30次后得到结果：

pk1=6.729 0e-009

xk=-0.000 0

-1.000 0

-0.000 0

hk=7.223 5e-009

可以看出算法是合理的，并且精确度很高，满足约束条件.

参考文献(References)：

[1]ROCKAFELLARRT.ConvexAnalysis[M].Princeton:PrincetonUniversityPress,1970

[2]GLOWINSKIR，LETP.AugmentedLagrangianandOperrator-splittingMethodsinNonlinearMechanics[M].SIAMStudiesinAppliedMathematics,1989

[3]UZAWAH,ARROWKJL.IternativeMethodsforConcaveProgrammingStudiesinLinearandNonlinearProgramming[M].StanfordUniversityPress,1958

[4]POLYAKBT.IntroductiontoOptimization[M].Optimi-zationSoftware,1987

[5]GONGC,MARCT.AProximal-basedDecompositionMe-thodforConvexMinimizatonProblems[J].MathematicalProgramming,1994,64:81-101

[6]DIMITRIP.ConvexOptimizationTheoryAthenaScientific[M].2009

[7]MASAOF.ApplicationoftheAlternatingDirectionMethodofMultiplierstoSeparableConvexProgrammingProblems[J].ComputationalOptimizationandApplication:1992(1):93-111

[8]XUMH,WUT.AClassofLinearizedProximalAlternatingDirectionMethods[J].OptimTheoryAppl,2011,151:321-337

责任编辑：田静

Separable Convex Optimization Problem Is Solved by PromotedPre-correction Neighboring Point Method

LUO Li

(School of Mathematics, Chongqing Normal University, Chongqing 401331, China)

Abstract：Objective function can be decomposed into n independent convex functions, and the constraint conditions for linear constraint can be divided into convex optimization problem. This paper presents a kind of promotion forecast correction multiplier method to solve separable convex optimization problem, this algorithm uses the second item in the iteration to replace the augmented Lagrangian function of the augmented items, and the proposed algorithm has both the characterization of neighboring multiplier method and parallel computation as well as can guarantee the global convergence under weak condition.

Key words：separable convex optimization; augmented Lagrangian; neighboring method; disintegrating method

中图分类号：O224

文献标志码：A

文章编号：1672-058X(2016)01-0019-04

作者简介：罗立(1990-)，女，重庆巫山人，硕士研究生，从事最优化理论与算法研究.

*基金项目：重庆市自然科学基金(CSTC2011JJA00010).

收稿日期：2015-07-22；修回日期：2015-08-10.

doi:10.16055/j.issn.1672-058X.2016.0001.004